diff --git a/README.md b/README.md
index fae38fd76d4bf05489264cedaa8c39e84ea6f54b..6288ae09352fd1043201043736afc705e35c4359 100644
--- a/README.md
+++ b/README.md
@@ -4,9 +4,10 @@ Welcome to the MPCDF **Python for HPC** tutorial!
## Authors
-* © 2018 - 2021 Sebastian Ohlmann (sebastian.ohlmann@mpcdf.mpg.de)
-* © 2018 - 2021 Klaus Reuter (klaus.reuter@mpcdf.mpg.de)
+* © 2022 Sebastian Kehl (sebastian.kehl@mpcdf.mpg.de)
* © 2020 Rafael Lago (rafael.lago@mpcdf.mpg.de)
+* © 2018 - 2022 Sebastian Ohlmann (sebastian.ohlmann@mpcdf.mpg.de)
+* © 2018 - 2022 Klaus Reuter (klaus.reuter@mpcdf.mpg.de)
[Max Planck Computing and Data Facility, Garching](https://mpcdf.mpg.de/)
@@ -35,6 +36,7 @@ Welcome to the MPCDF **Python for HPC** tutorial!
* multiprocessing
* mpi4py
* Running parallel Python programs with SLURM
+ * Parallelization frameworks, e.g. Dask and Ray
* Software engineering with Python
* Testing
* Packaging
diff --git a/examples/cython/c_interface/README.md b/examples/cython/c_interface/README.md
index ef817270a6664451b7b2c8791f9e391d256c4fc2..4f858d87f3c1aa0f7198d4c3a6bd65ceadf0169d 100644
--- a/examples/cython/c_interface/README.md
+++ b/examples/cython/c_interface/README.md
@@ -10,9 +10,9 @@
## Usage
* quick test in the current directory
- `python setup.py build_ext --inplace`
+ `pip install -e .`
`python -c "from foobar import hello; hello.say_hello()"`
+ or run `test_foobar.py`
* or install the package, and run the extension from anywhere
- `python setup.py install --user`
-* run `test_foobar.py` to call the compiled code example
+ `pip install --user`
diff --git a/examples/cython/c_interface/pyproject.toml b/examples/cython/c_interface/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..7af57b83c23e1a3f27ed9c9c506a01296cb225ee
--- /dev/null
+++ b/examples/cython/c_interface/pyproject.toml
@@ -0,0 +1,10 @@
+[build-system]
+requires = ["setuptools", "cython"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "foobar"
+version = "0.0.1"
+
+[tool.setuptools.package-data]
+foobar = ["*.h"]
diff --git a/examples/cython/c_interface/setup.py b/examples/cython/c_interface/setup.py
index c8db1139946062e428e5290c69c34300624ab92b..048970016010be13a3e1201306dd5b6634a43425 100644
--- a/examples/cython/c_interface/setup.py
+++ b/examples/cython/c_interface/setup.py
@@ -5,6 +5,6 @@ ext = Extension("foobar.hello",
sources=["foobar/hello.pyx", "foobar/c_hello.c"]
)
-setup(name="foobar",
- ext_modules=[ext],
+setup(
+ ext_modules=[ext],
)
diff --git a/examples/cython/c_interface/test_foobar.py b/examples/cython/c_interface/test_foobar.py
index 74b524c97163de3087cd84830d89ff37a94e1980..eea2b682ccb88e4f18f8bf930646f04acf40d6ee 100755
--- a/examples/cython/c_interface/test_foobar.py
+++ b/examples/cython/c_interface/test_foobar.py
@@ -3,7 +3,7 @@
try:
from foobar import hello
except:
- print("Please compile first using `python setup.py build_ext --inplace`")
+ print("Please compile first using `pip install -e .`")
else:
hello.say_hello()
diff --git a/examples/cython/c_interface_shared_object/README.md b/examples/cython/c_interface_shared_object/README.md
index 8eb9e405f08eda20de461c84fed1e133334f8f46..60b654d01f41edd136731505fc1ebae9cfdcedb4 100644
--- a/examples/cython/c_interface_shared_object/README.md
+++ b/examples/cython/c_interface_shared_object/README.md
@@ -2,7 +2,7 @@
## Features
-* Python module "wrap_libhello" lives in the directory "wrap_libhello" (has `__index__.py`)
+* Python module "hello" lives in the package-directory "wrap_libhello" (has `__init__.py`)
* `hello.pyx` contains the Python interface written in Cython
* `c_hello.c` contains a hello-world implementation in C, however, in contrast
to the previous simple example it is located in a different library (.so,
@@ -13,9 +13,10 @@
## Usage
+* set enviroment variable HELLO_ROOT to point to libhello, e.g., from
+ the current directory `export HELLO_ROOT=$(pwd)/libhello/`
* quick test in the current directory
- `python setup.py build_ext --inplace`
- `python -c "from wrap_libhello import hello; hello.say_hello()"`
+ `pip install -e --user .`
+ run `test_wrap_libhello.py` to call the function in the shared object
* or install the package, and run the extension from anywhere
- `python setup.py install --user`
-* run `test_wrap_libhello.py` to call the function in the shared object
+ `python install . --user`
diff --git a/examples/cython/c_interface_shared_object/pyproject.toml b/examples/cython/c_interface_shared_object/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..3576908a759efdb8acc6dc515fbe088e249bcc0a
--- /dev/null
+++ b/examples/cython/c_interface_shared_object/pyproject.toml
@@ -0,0 +1,13 @@
+[build-system]
+requires = ["setuptools", "cython"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "wrap_libhello"
+version = "0.1"
+
+[tool.setuptools.packages.find]
+exclude = ["libhello"]
+
+[tool.setuptools.package-data]
+wrap_libhello = ["*.h"]
diff --git a/examples/cython/c_interface_shared_object/setup.py b/examples/cython/c_interface_shared_object/setup.py
index 1646a169537267e705cebf210d1d3c82b2fe474c..a341c65f76276cb5bc03eda19b9715ad878a9b02 100644
--- a/examples/cython/c_interface_shared_object/setup.py
+++ b/examples/cython/c_interface_shared_object/setup.py
@@ -1,7 +1,12 @@
import os
from setuptools import setup, Extension
-libhello_dir = os.path.abspath("./libhello")
+try:
+ libhello_root = os.environ["HELLO_ROOT"]
+except KeyError as e:
+ raise ValueError("Set path to libhello in environment variable HELLO_ROOT")
+
+libhello_dir = os.path.abspath(libhello_root)
# We need to specify the location of the include file.
include_dirs = []
@@ -21,6 +26,6 @@ ext = Extension("wrap_libhello.hello",
include_dirs=include_dirs
)
-setup(name="wrap_libhello",
- ext_modules=[ext],
+setup(
+ ext_modules=[ext],
)
diff --git a/examples/cython/c_numpy/README.md b/examples/cython/c_numpy/README.md
index 6ccd25cefc09ec74b9301aee8ae45dd529dfd05a..2ba7cbfad028b0bf746e100a4a1330188532c5b7 100644
--- a/examples/cython/c_numpy/README.md
+++ b/examples/cython/c_numpy/README.md
@@ -10,8 +10,8 @@
## Usage
-* quick test in the current directory
- `python setup.py build_ext --inplace`
+* quick test in the current directory
+ `pip install -e .`
`./test_ctonumpy.py`
* or install the package, and run the extension from anywhere
diff --git a/examples/cython/c_numpy/pyproject.toml b/examples/cython/c_numpy/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..8a88d064ac9b3cf81df2b5673c519dfe051289b9
--- /dev/null
+++ b/examples/cython/c_numpy/pyproject.toml
@@ -0,0 +1,10 @@
+[build-system]
+requires = ["setuptools", "cython", "numpy"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "ctonumpy"
+version = "0.0.1"
+
+[tool.setuptools.package-data]
+ctonumpy = ["*.h"]
diff --git a/examples/cython/c_numpy/setup.py b/examples/cython/c_numpy/setup.py
index 0ee82e9b335e171a5d8614d6f37f47664e5fa76e..a038f2e16a28c1f6906e62bcd2479f858fc06ae3 100644
--- a/examples/cython/c_numpy/setup.py
+++ b/examples/cython/c_numpy/setup.py
@@ -26,7 +26,7 @@ ext = Extension("ctonumpy.cube",
include_dirs=[np.get_include()]
)
-setup(name="ctonumpy",
- ext_modules=[ext],
+setup(
+ ext_modules=[ext],
)
diff --git a/examples/cython/hello_world/README.md b/examples/cython/hello_world/README.md
index ce1d84fe475ff94447dbe971ec07fe960a91d7bb..97074d15cb3a405cc93a3c3f5780c0e16274c659 100644
--- a/examples/cython/hello_world/README.md
+++ b/examples/cython/hello_world/README.md
@@ -2,7 +2,7 @@
Run the following commands to build and run the example:
1. python setup.py config
-2. python setup.py build_ext --inplace
+2. pip install -e .
3. python -c "import hello_world; hello_world.say_hello()"
Explanation:
diff --git a/examples/cython/hello_world/hello_world/__init__.py b/examples/cython/hello_world/hello_world/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..9d215565218d85c266d1943b56515a70786fb2e1
--- /dev/null
+++ b/examples/cython/hello_world/hello_world/__init__.py
@@ -0,0 +1 @@
+from .hello_world import *
diff --git a/examples/cython/hello_world/hello_world.pyx b/examples/cython/hello_world/hello_world/hello_world.pyx
similarity index 100%
rename from examples/cython/hello_world/hello_world.pyx
rename to examples/cython/hello_world/hello_world/hello_world.pyx
diff --git a/examples/cython/hello_world/pyproject.toml b/examples/cython/hello_world/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..2b7d1a8a91e4fd1eab81070f91ad6e580bc7b8a7
--- /dev/null
+++ b/examples/cython/hello_world/pyproject.toml
@@ -0,0 +1,10 @@
+[build-system]
+requires = ["setuptools", "cython"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "hello_world"
+version = "0.0.1"
+
+[tool.setuptools.package-data]
+hello_world = ["hello_world.pyx"]
diff --git a/examples/cython/hello_world/setup.py b/examples/cython/hello_world/setup.py
index dd7fb8a182aacfdf92cd0c35f74d5ef3c76485ba..9f1d4d7ac813b8062704bc6283f64cac263e20ba 100644
--- a/examples/cython/hello_world/setup.py
+++ b/examples/cython/hello_world/setup.py
@@ -1,5 +1,6 @@
from setuptools import setup
from Cython.Build import cythonize
-setup(name = "hello_world",
- ext_modules = cythonize("hello_world.pyx"))
+setup(
+ ext_modules = cythonize("hello_world/hello_world.pyx")
+)
diff --git a/examples/pybind11/pyproject.toml b/examples/pybind11/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..01f1c1e406892f373a099ada6c688bf70c15a76d
--- /dev/null
+++ b/examples/pybind11/pyproject.toml
@@ -0,0 +1,7 @@
+[build-system]
+requires = ["setuptools", "pybind11[global]"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "pybex"
+version = "0.0.1"
diff --git a/examples/pycuda/README b/examples/pycuda/README
new file mode 100644
index 0000000000000000000000000000000000000000..f56f4a0633ab655fb9df907d47a34475efe247ab
--- /dev/null
+++ b/examples/pycuda/README
@@ -0,0 +1 @@
+This example is not used anymore because teaching CUDA is out of scope for this course.
diff --git a/examples/setuptools/minimal/helloworld/cli.py b/examples/setuptools/minimal/helloworld/cli.py
new file mode 100755
index 0000000000000000000000000000000000000000..9c1327e7b000a3352274efd1498a2cd1765546d4
--- /dev/null
+++ b/examples/setuptools/minimal/helloworld/cli.py
@@ -0,0 +1,4 @@
+from . import say_hello
+
+def hello_world():
+ say_hello()
diff --git a/examples/setuptools/minimal/pyproject.toml b/examples/setuptools/minimal/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..073b443c215c276b2503d801f998fba5d04b1827
--- /dev/null
+++ b/examples/setuptools/minimal/pyproject.toml
@@ -0,0 +1,23 @@
+[build-system]
+requires = ["setuptools"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "helloworld"
+version = "0.1"
+# name of the software package (as it would appear on PyPI)
+description = "example package that prints hello world"
+# dependencies = ["numpy"]
+authors = [
+ {name = "John Doe", email = "john.doe@example.mpg.de"}
+]
+license = {text = "PSF"}
+keywords = ["hello", "world", "example"]
+
+[project.urls]
+homepage = "https://example.mpg.de/helloworld/"
+
+# list of executable(s) that come with the package (if applicable)
+[project.scripts]
+hello-world = "helloworld.cli:hello_world"
+
diff --git a/examples/setuptools/minimal/say_hello.py b/examples/setuptools/minimal/say_hello.py
deleted file mode 100755
index 764c141eed1961b91714561f9403fe1cfc5d8042..0000000000000000000000000000000000000000
--- a/examples/setuptools/minimal/say_hello.py
+++ /dev/null
@@ -1,3 +0,0 @@
-#!/usr/bin/env python3
-import helloworld
-helloworld.say_hello()
diff --git a/examples/setuptools/minimal/setup.py b/examples/setuptools/minimal/setup.py
deleted file mode 100644
index 5c1e25cc54245dc8df37c1957b8ed196b7c87721..0000000000000000000000000000000000000000
--- a/examples/setuptools/minimal/setup.py
+++ /dev/null
@@ -1,20 +0,0 @@
-from setuptools import setup
-
-setup(
- # name of the software package (as it would appear on PyPI)
- name="helloworld",
- version="0.1",
- # list of the Python modules provided by the package
- packages=["helloworld"],
- # list of executable(s) that come with the package (if applicable)
- scripts=['say_hello.py'],
- # list of package dependencies (if necessary)
- #install_requires=['numpy'],
- # more information, necessary for an upload to PyPI
- author="John Doe",
- author_email="john.doe@example.mpg.de",
- description="example package that prints hello world",
- license="PSF",
- keywords="hello world example",
- url="https://example.mpg.de/helloworld/", # project home page, if any
-)
diff --git a/examples/setuptools/py-test/HelloWorld/cli.py b/examples/setuptools/py-test/HelloWorld/cli.py
new file mode 100755
index 0000000000000000000000000000000000000000..9c1327e7b000a3352274efd1498a2cd1765546d4
--- /dev/null
+++ b/examples/setuptools/py-test/HelloWorld/cli.py
@@ -0,0 +1,4 @@
+from . import say_hello
+
+def hello_world():
+ say_hello()
diff --git a/examples/setuptools/py-test/README.txt b/examples/setuptools/py-test/README.txt
index 863bbea4222bc9174bdc079804fe0de3fcedf32a..091ed62b0d3e1819cbb87ed68aa5d4d84ad1fe9e 100644
--- a/examples/setuptools/py-test/README.txt
+++ b/examples/setuptools/py-test/README.txt
@@ -1,5 +1,4 @@
Run
-python setup.py pytest
-
-to do the tests via setup.py.
+pip install .[tests]
+pytest -v tests/
diff --git a/examples/setuptools/py-test/pyproject.toml b/examples/setuptools/py-test/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..540c87e295b2c3247b4df3c55a7e3127f0ab87b5
--- /dev/null
+++ b/examples/setuptools/py-test/pyproject.toml
@@ -0,0 +1,25 @@
+[build-system]
+requires = ["setuptools"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "HelloWorld"
+version = "0.1"
+description = "This is an example package"
+dependencies = ["numpy"]
+authors = [
+ {name = "John Doe", email = "john.doe@example.mpg.de"}
+]
+license = {text = "PSF"}
+keywords = ["hello", "world", "example"]
+
+[project.optional-dependencies]
+tests = ["pytest"]
+
+[project.urls]
+homepage = "https://example.mpg.de/HelloWorld/"
+
+# list of executable(s) that come with the package (if applicable)
+[project.scripts]
+hello-world = "HelloWorld.cli:hello_world"
+
diff --git a/examples/setuptools/py-test/say_hello.py b/examples/setuptools/py-test/say_hello.py
deleted file mode 100755
index 47f1202183e998ede14affa6e80eb27a06705a8f..0000000000000000000000000000000000000000
--- a/examples/setuptools/py-test/say_hello.py
+++ /dev/null
@@ -1,3 +0,0 @@
-#!/usr/bin/env python3
-import HelloWorld
-HelloWorld.say_hello()
diff --git a/examples/setuptools/py-test/setup.py b/examples/setuptools/py-test/setup.py
deleted file mode 100644
index d1be2de705e325de863037f9b6b5e70da3868fd8..0000000000000000000000000000000000000000
--- a/examples/setuptools/py-test/setup.py
+++ /dev/null
@@ -1,20 +0,0 @@
-from setuptools import setup
-setup(
- name="HelloWorld",
- version="0.1",
- # specify a list of the packages (subdirectory with __init__.py file)
- packages=["HelloWorld"],
- # executable that comes with the package (if applicable)
- scripts=['say_hello.py'],
- # software dependencies (if necessary)
- install_requires=['numpy'],
- setup_requires=['pytest-runner'],
- tests_require=['pytest'],
- # metadata for upload to PyPI
- author="Me",
- author_email="me@example.com",
- description="This is an Example Package",
- license="PSF",
- keywords="hello world example examples",
- url="http://example.com/HelloWorld/", # project home page, if any
-)
diff --git a/examples/setuptools/sphinx-doc/README.txt b/examples/setuptools/sphinx-doc/README.txt
index 5c9af44b1bf98428f4213e9e6491dd2314d6eaa5..e0409504b54c296702834c96864b01e35c379fa6 100644
--- a/examples/setuptools/sphinx-doc/README.txt
+++ b/examples/setuptools/sphinx-doc/README.txt
@@ -9,10 +9,10 @@ To generate the documentation,
install the package first to make it importable
- python setup.py develop --user
+ pip install .[doc]
and run
- python setup.py build_sphinx
+ sphinx-build -b html doc/ doc/_build
to generate the HTML documentation.
diff --git a/examples/setuptools/sphinx-doc/pyproject.toml b/examples/setuptools/sphinx-doc/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..21d2846558e42b5aaf0178ec35e6c4be07f9dcfa
--- /dev/null
+++ b/examples/setuptools/sphinx-doc/pyproject.toml
@@ -0,0 +1,19 @@
+[build-system]
+requires = ["setuptools"]
+build-backend = "setuptools.build_meta"
+
+[project]
+name = "HelloWorld"
+version = "0.1"
+description = "This is an example package"
+authors = [
+ {name = "John Doe", email = "john.doe@example.mpg.de"}
+]
+license = {text = "PSF"}
+keywords = ["hello", "world", "example"]
+
+[project.optional-dependencies]
+doc = ["sphinx"]
+
+[project.urls]
+homepage = "https://example.mpg.de/HelloWorld/"
diff --git a/examples/setuptools/sphinx-doc/say_hello.py b/examples/setuptools/sphinx-doc/say_hello.py
deleted file mode 100755
index 47f1202183e998ede14affa6e80eb27a06705a8f..0000000000000000000000000000000000000000
--- a/examples/setuptools/sphinx-doc/say_hello.py
+++ /dev/null
@@ -1,3 +0,0 @@
-#!/usr/bin/env python3
-import HelloWorld
-HelloWorld.say_hello()
diff --git a/examples/setuptools/sphinx-doc/setup.cfg b/examples/setuptools/sphinx-doc/setup.cfg
deleted file mode 100644
index 8217837115e0c6321c6c7a4012f5fbb9966c5afc..0000000000000000000000000000000000000000
--- a/examples/setuptools/sphinx-doc/setup.cfg
+++ /dev/null
@@ -1,6 +0,0 @@
-[build_sphinx]
-all-files = 1
-source-dir = doc/
-build-dir = doc/
-# the following option is only available with sphinx >= 1.5
-warning_is_error = 1
diff --git a/examples/setuptools/sphinx-doc/setup.py b/examples/setuptools/sphinx-doc/setup.py
deleted file mode 100644
index bcc7609239d727f198a60dc07547122a192154c6..0000000000000000000000000000000000000000
--- a/examples/setuptools/sphinx-doc/setup.py
+++ /dev/null
@@ -1,18 +0,0 @@
-from setuptools import setup
-setup(
- name="HelloWorld",
- version="0.1",
- # specify a list of the packages (subdirectory with __init__.py file)
- packages=["HelloWorld"],
- # executable that comes with the package (if applicable)
- scripts=['say_hello.py'],
- # software dependencies (if necessary)
- # install_requires=['docutils>=0.3'],
- # metadata for upload to PyPI
- author="Me",
- author_email="me@example.com",
- description="This is an Example Package",
- license="PSF",
- keywords="hello world example examples",
- url="http://example.com/HelloWorld/", # project home page, if any
-)
diff --git a/exercises/Software_engineering_Exercise.ipynb b/exercises/Software_engineering_Exercise.ipynb
index f8b909c451646b80cbb429393a6d566344151a70..fa72ad3cf4a84fd633f047757f6035624dc32bcc 100644
--- a/exercises/Software_engineering_Exercise.ipynb
+++ b/exercises/Software_engineering_Exercise.ipynb
@@ -15,22 +15,22 @@
"source": [
"1. Create a file (`arithmetic.py`) with two functions: `add` and `multiply` that add and multiply two numbers, respectively, and return the result\n",
"2. Now we need to make a package out of this: create a new folder (e.g. `algebra`) and move the file `arithmetic.py` there. To make a package out of it, create the empty file `__init__.py` in this folder.\n",
- "3. Add the following simple `setup.py` file to the base directory\n",
- "```python\n",
- "from setuptools import setup\n",
- "setup(\n",
- " name=\"Algebra\",\n",
- " version=\"0.1\",\n",
- " # specify a list of the packages (subdirectory with __init__.py file)\n",
- " packages=[\"algebra\"],\n",
- " # metadata for upload to PyPI\n",
- " author=\"Me\",\n",
- " author_email=\"me@example.com\",\n",
- " description=\"This is an Example Package\",\n",
- " license=\"PSF\"\n",
- ")\n",
- "```\n",
- "4. Test the package: run `pip install -e ./ --user` to install a development version; change to your home directory, start a python shell and try to run `from algebra.arithmetic import add`.\n",
+ "3. Add the following simple `pyproject.toml` file to the base directory\n",
+ " ```toml\n",
+ " [build-system]\n",
+ " requires = [\"setuptools\"]\n",
+ " build-backend = \"setuptools.build_meta\"\n",
+ "\n",
+ " [project]\n",
+ " name = \"algebra\"\n",
+ " version = \"0.1\"\n",
+ " description = \"This is an example package.\"\n",
+ " authors = [\n",
+ " {name = \"me\", email = \"me@example.com\"}\n",
+ " ]\n",
+ " license = {text = \"PSF\"}\n",
+ " ```\n",
+ "4. Test the package: run `pip install -e . --user` to install a development version; change to your home directory, start a python shell and try to run `from algebra.arithmetic import add`.\n",
"5. Now we want to add tests:\n",
" * create a folder `tests`\n",
" * create a file `test_arithmetic.py` (needs to start with `test_`)\n",
@@ -41,12 +41,13 @@
" result = add(3, 5)\n",
" assert(result == 8)\n",
"```\n",
- " * add the following lines to the setup call in `setup.py`:\n",
- "```python\n",
- " setup_requires=['pytest-runner'],\n",
- " tests_require=['pytest'],\n",
+ " * add the following lines to `pyproject.toml`:\n",
+ "```toml\n",
+ "[project.optional-dependencies]\n",
+ "tests = [\"pytest\"]\n",
"```\n",
- " * Run the tests with `python setup.py pytest` (alternatively you can call `pytest`).\n",
+ " * Install the package with automatic dependency resolution `pip install -e .[tests] --user`\n",
+ " * Run the tests from the base directory with `pytest -v`.\n",
"6. Add a test for the multiplication routine\n",
"\n",
"Congratulations! You created a package including tests. Our recommendation is to always create packages for your python software. Moreover, adding tests is very important to validate your code and to ensure that new developments do not break current functionality."
diff --git a/exercises/_solutions/Software_engineering_Exercise_withsolution.ipynb b/exercises/_solutions/Software_engineering_Exercise_withsolution.ipynb
index 83c660b6d0ce467bf86d0d124b2db11ed9d010f8..fa72ad3cf4a84fd633f047757f6035624dc32bcc 100644
--- a/exercises/_solutions/Software_engineering_Exercise_withsolution.ipynb
+++ b/exercises/_solutions/Software_engineering_Exercise_withsolution.ipynb
@@ -15,22 +15,22 @@
"source": [
"1. Create a file (`arithmetic.py`) with two functions: `add` and `multiply` that add and multiply two numbers, respectively, and return the result\n",
"2. Now we need to make a package out of this: create a new folder (e.g. `algebra`) and move the file `arithmetic.py` there. To make a package out of it, create the empty file `__init__.py` in this folder.\n",
- "3. Add the following simple `setup.py` file to the base directory\n",
- "```python\n",
- "from setuptools import setup\n",
- "setup(\n",
- " name=\"Algebra\",\n",
- " version=\"0.1\",\n",
- " # specify a list of the packages (subdirectory with __init__.py file)\n",
- " packages=[\"algebra\"],\n",
- " # metadata for upload to PyPI\n",
- " author=\"Me\",\n",
- " author_email=\"me@example.com\",\n",
- " description=\"This is an Example Package\",\n",
- " license=\"PSF\"\n",
- ")\n",
- "```\n",
- "4. Test the package: run `pip install -e ./ --user` to install a development version; change to your home directory, start a python shell and try to run `from algebra.arithmetic import add`.\n",
+ "3. Add the following simple `pyproject.toml` file to the base directory\n",
+ " ```toml\n",
+ " [build-system]\n",
+ " requires = [\"setuptools\"]\n",
+ " build-backend = \"setuptools.build_meta\"\n",
+ "\n",
+ " [project]\n",
+ " name = \"algebra\"\n",
+ " version = \"0.1\"\n",
+ " description = \"This is an example package.\"\n",
+ " authors = [\n",
+ " {name = \"me\", email = \"me@example.com\"}\n",
+ " ]\n",
+ " license = {text = \"PSF\"}\n",
+ " ```\n",
+ "4. Test the package: run `pip install -e . --user` to install a development version; change to your home directory, start a python shell and try to run `from algebra.arithmetic import add`.\n",
"5. Now we want to add tests:\n",
" * create a folder `tests`\n",
" * create a file `test_arithmetic.py` (needs to start with `test_`)\n",
@@ -41,12 +41,13 @@
" result = add(3, 5)\n",
" assert(result == 8)\n",
"```\n",
- " * add the following lines to the setup call in `setup.py`:\n",
- "```python\n",
- " setup_requires=['pytest-runner'],\n",
- " tests_require=['pytest'],\n",
+ " * add the following lines to `pyproject.toml`:\n",
+ "```toml\n",
+ "[project.optional-dependencies]\n",
+ "tests = [\"pytest\"]\n",
"```\n",
- " * Run the tests with `python setup.py pytest` (alternatively you can call `pytest`).\n",
+ " * Install the package with automatic dependency resolution `pip install -e .[tests] --user`\n",
+ " * Run the tests from the base directory with `pytest -v`.\n",
"6. Add a test for the multiplication routine\n",
"\n",
"Congratulations! You created a package including tests. Our recommendation is to always create packages for your python software. Moreover, adding tests is very important to validate your code and to ensure that new developments do not break current functionality."
@@ -74,4 +75,4 @@
},
"nbformat": 4,
"nbformat_minor": 4
-}
+}
\ No newline at end of file
diff --git a/notebooks/1a--Teaser_Diffusion.ipynb b/notebooks/1a--Teaser_Diffusion.ipynb
index 89b5aadc476ee9d6bd07942ba4502a8f18261add..8f1a6f574b8c7b18d0fe44e218fbf1c9f5bbafdc 100644
--- a/notebooks/1a--Teaser_Diffusion.ipynb
+++ b/notebooks/1a--Teaser_Diffusion.ipynb
@@ -12,8 +12,6 @@
"\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -353,7 +351,7 @@
}
},
"source": [
- "## Conclusion: Python in HPC\n",
+ "## Conclusion: Python for HPC\n",
"* Python: rapid development of code\n",
"* With some tricks and some effort, good performance possible\n",
"\n",
@@ -364,7 +362,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -378,7 +376,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/1b--Introduction.ipynb b/notebooks/1b--Introduction.ipynb
index f10683a6aaffb206ddf3b509d21bd41b36547d11..eec05cd389617bb1550e5bb11ac8f29b2eadc2d8 100644
--- a/notebooks/1b--Introduction.ipynb
+++ b/notebooks/1b--Introduction.ipynb
@@ -12,7 +12,9 @@
"\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
+ "Sebastian Kehl, Sebastian Ohlmann, Klaus Reuter\n",
+ "\n",
+ "_15-17 November 2022_\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -47,7 +49,7 @@
"### [GPAW](https://wiki.fysik.dtu.dk/gpaw/)\n",
"\n",
"* Density-functional theory code for material science\n",
- "* Implemented as a Python module (C++ core, Python UI)\n",
+ "* Implemented as a Python module (C core, Python UI)\n",
"* Parallelization: MPI + OpenMP, scales to O(10k) cores\n",
"\n",
"### [ESPResSo++](http://www.espresso-pp.de)\n",
@@ -224,7 +226,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.8.3"
}
},
"nbformat": 4,
diff --git a/notebooks/1c--Python_Refresher.ipynb b/notebooks/1c--Python_Refresher.ipynb
index 05b09c6c2e4f5506eb758de2b5b9fb2de5831eec..db7be75d8686aa03e6bd67034147eb5388f33d2f 100644
--- a/notebooks/1c--Python_Refresher.ipynb
+++ b/notebooks/1c--Python_Refresher.ipynb
@@ -12,7 +12,6 @@
"\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -1265,7 +1264,6 @@
" * code does not need to be changed, reads in parameter file\n",
"* recommended\n",
" * YAML\n",
- " * (JSON)\n",
"* less recommended\n",
" * configparser (\".cfg\")\n",
" * custom formats"
@@ -1359,79 +1357,6 @@
"```"
]
},
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "#### JSON\n",
- "* available via the `json` package\n",
- "* part of Python's standard library\n",
- "* technically, JSON is a subset of YAML"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 32,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": [
- "# write the par object to a well-formatted JSON file\n",
- "import json\n",
- "with open(\"par.json\", 'w') as fp:\n",
- " json.dump(par, fp, sort_keys=True, indent=4)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 33,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": [
- "# read the parameters back from JSON\n",
- "with open(\"par.json\", 'r') as fp:\n",
- " par_j = json.load(fp)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "#### JSON\n",
- "\n",
- "```json\n",
- "{\n",
- " \"general\": {\n",
- " \"resolution\": [\n",
- " 1024,\n",
- " 1024,\n",
- " 512\n",
- " ],\n",
- " \"time_steps\": 1000\n",
- " },\n",
- " \"species\": {\n",
- " \"H\": false,\n",
- " \"N\": true\n",
- " }\n",
- "}%\n",
- "```"
- ]
- },
{
"cell_type": "markdown",
"metadata": {
@@ -1453,7 +1378,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1467,7 +1392,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/1d--BasicHPC.ipynb b/notebooks/1d--BasicHPC.ipynb
index 8b8eda8eba817deb349bc2e01573757f2724dd24..b9e77f143ebb545a6a5100f263594c2225b7cc1b 100644
--- a/notebooks/1d--BasicHPC.ipynb
+++ b/notebooks/1d--BasicHPC.ipynb
@@ -10,9 +10,7 @@
"source": [
"# Basics of High Performance Computing\n",
"\n",
- "**Python for HPC**\n",
- "\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
+ "**Python for HPC course**\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -47,8 +45,8 @@
"* High performance computing: \"computing at bottlenecks of the hardware\" (G. Hager, RRZE)\n",
"* Write *efficient software* to use *maximum hardware potential*\n",
"* Common bottlenecks:\n",
- " * Floating point operations per second (FLOPS)\n",
- " * Memory access, memory bandwidth (GB/s)\n",
+ " * Floating point operations\n",
+ " * Memory access\n",
" * Input/Output\n",
" * Communication\n",
"* Needed:\n",
@@ -88,7 +86,9 @@
"* Cluster → nodes\n",
"* Node → sockets (CPUs), GPUs\n",
"* CPU → cores\n",
- "* Core → single instruction, multiple data (SIMD)"
+ "* Core → single instruction, multiple data (SIMD)\n",
+ "\n",
+ "More on exploiting parallelism later in the course."
]
},
{
@@ -109,6 +109,9 @@
"* Back end:\n",
" * Execute instructions on data\n",
" * Transfer data between registers and memory\n",
+ "* Operates at a certain frequency\n",
+ "* Processes a certain number\n",
+ " of operations per second\n",
"\n",
"Possible bottleneck: number of floating point operations per second (FLOPS)\n"
]
@@ -123,9 +126,10 @@
"source": [
"## Memory access\n",
"\n",
- "<img src=\"fig/memory_hierarchy.svg\" style=\"float:right; width=35%\" />\n",
+ "<img src=\"fig/memory_hierarchy.svg\" style=\"float:right; width:35%\" />\n",
"\n",
"* HPC codes need data to work on\n",
+ "* Data needs to be brought to the CPU\n",
"* Memory much slower than CPU $\\to$ often a bottleneck\n",
"* Mitigation: **memory hierarchy** [[Nice animation]](http://www.overbyte.com.au/misc/Lesson3/CacheFun.html):\n",
"* Cache is filled from memory in small chunks (cache lines)\n",
@@ -405,7 +409,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -419,7 +423,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.3"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/2a--NumPy.ipynb b/notebooks/2a--NumPy.ipynb
index 5914dd81737c143be7337836f32e842db3bec07a..a63227d9c8881c1af9f4e11018dc53fa6d400f9c 100644
--- a/notebooks/2a--NumPy.ipynb
+++ b/notebooks/2a--NumPy.ipynb
@@ -12,9 +12,6 @@
"\n",
"**Python for HPC**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter \n",
- "2020 Rafael Lago\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -44,7 +41,7 @@
"source": [
"## Performance Problem - Loops\n",
"\n",
- "* Looping in Python (and most interpreted languages) can be *<span style=\"color:red\">very expensive</span>*\n",
+ "* Looping in Python (and most interpreted languages) can be **very expensive**\n",
"* Numerical codes perform mostly array computation\n",
"* Example: Discrete Fourier Transform\n",
"\n",
@@ -460,7 +457,7 @@
"# new dimensions can be added\n",
"z = np.arange(3)\n",
"print(\"z:\")\n",
- "print(z[:])"
+ "print(z[:,np.newaxis])"
]
},
{
@@ -862,9 +859,9 @@
"\n",
"\n",
"* Takeaway messages:\n",
- " 1. <span style=\"color:red\">High level manipulations $\\to$ in Python</span>\n",
- " 2. <span style=\"color:red\">Intensive computation $\\to$ delegate to underlying libraries</span>\n",
- " 3. <span style=\"color:red\">No dedicated library $\\to$ use NumPy arrays and their functions</span>\n",
+ " 1. High level manipulations $\\to$ in Python\n",
+ " 2. Intensive computation $\\to$ delegate to underlying libraries\n",
+ " 3. No dedicated library $\\to$ use NumPy arrays and their functions\n",
"\n",
"<br>\n",
"\n",
@@ -993,8 +990,8 @@
"\n",
"\n",
"* different sparse formats for different tasks:\n",
- " * CSR: for row operations/slicing\n",
- " * CSC: for column operations/slicing\n",
+ " * CSR: compressed sparse row, for row operations/slicing\n",
+ " * CSC: compressed sparse column, for column operations/slicing\n",
" * LIL: list-of-lists, efficient for building the matrix, slow for most other operations\n",
" * DIA: diagonal matrix, very useful for FD\n",
" * `speye()`: sparse identity\n"
@@ -1041,38 +1038,6 @@
"%time Mlil = fill_matrix(Mlil).tocsr()"
]
},
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### SciPy Example 3: Sparse Matrices"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": [
- "# conversion functions to several different matrix formats\n",
- "M = Mlil.todia() # fires a warning if there are too many diagonals\n",
- "M = Mlil.tocsr()\n",
- "M = Mlil.tocsc()\n",
- "M = Mlil.todense()\n",
- "\n",
- "# constructors can receive matrices from other formats too\n",
- "M = sparse.csr_matrix(Mlil, dtype=np.int32)\n",
- "M"
- ]
- },
{
"cell_type": "markdown",
"metadata": {
@@ -1126,62 +1091,20 @@
"import scipy.sparse.linalg as splinalg\n",
"import numpy as np\n",
"\n",
- "n = 1000\n",
- "b = np.random.random(n)\n",
+ "def compare_density(density, n=1000):\n",
+ " b = np.random.random(n)\n",
+ " A1 = sparse.random(n, n, density=density, format='csr')\n",
+ " A1 += sparse.eye(n,n, format='csr')\n",
+ " print(\"Density: \", density)\n",
+ " print(\"Sparse: \")\n",
+ " %timeit splinalg.spsolve(A1, b)\n",
+ " A2 = A1.todense()\n",
+ " print(\"Dense: \")\n",
+ " %timeit linalg.solve(A2, b)\n",
"\n",
"# Density=0.001: sparse is faster, Density=0.01: dense is faster\n",
- "A1 = sparse.random(n, n, density=0.1, format='csr')\n",
- "A1 += sparse.eye(n,n, format='csr')\n",
- "print(\"NNZ: \", A1.nnz)\n",
- "%time x1 = splinalg.spsolve(A1, b)\n",
- "\n",
- "A2 = A1.todense()\n",
- "%time x2 = linalg.solve(A2, b)\n",
- "\n",
- "np.allclose(x1, x2)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## SciPy - Further Linear Algebra Functions\n",
- "\n",
- "* Matrix-matrix and matrix-vector products \n",
- " * careful with preservation of sparsity!\n",
- "* Solve linear systems\n",
- "* Compute eigenvalues and singular values\n",
- "* Compute pseudoinverse"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "outputs": [],
- "source": [
- "# Matrix-Vector product syntax\n",
- "y1 = A1*b\n",
- "y2 = A2*b[:,None]\n",
- "y3 = A1.dot(b)\n",
- "y4 = A2.dot(b)\n",
- "print(np.allclose(y1[:,None], y2))\n",
- "print(np.allclose(y1, y3))\n",
- "print(np.allclose(y1, y4))\n",
- "# Matrix-matrix Product - accepts different formats\n",
- "M = A1*A2\n",
- "print(\"A1*A2 - sparsity preserved?\", sparse.issparse(M))\n",
- "A3 = sparse.random(n, n, density=0.01, format='csr')\n",
- "M = A1*A3\n",
- "print(\"A1*A3 - sparsity preserved?\", sparse.issparse(M))"
+ "compare_density(0.01)\n",
+ "compare_density(0.001)"
]
},
{
@@ -1951,7 +1874,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1965,7 +1888,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.3"
+ "version": "3.9.7"
},
"rise": {
"enable_chalkboard": true,
diff --git a/notebooks/2b--Cython.ipynb b/notebooks/2b--Cython.ipynb
index 647474cf867193078c082dcc8da7218d7426b99c..bc83c310ed56cdf428b85f64d9ff89695b7f1085 100644
--- a/notebooks/2b--Cython.ipynb
+++ b/notebooks/2b--Cython.ipynb
@@ -11,7 +11,6 @@
"# Cython\n",
"**Python for HPC course**\n",
"\n",
- "2018 - 2021 Sebastian Ohlmann, Klaus Reuter\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -132,8 +131,10 @@
},
"source": [
"```bash\n",
- "# compilation of the cython extension\n",
+ "# explicit compilation of the cython extension\n",
"$ python setup.py build_ext --inplace\n",
+ "# or compilation from the build-backend during installation\n",
+ "$ pip install .\n",
"```"
]
},
@@ -396,7 +397,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -410,7 +411,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/2c--Numba.ipynb b/notebooks/2c--Numba.ipynb
index c0bce0439d565384212234add5c1ffbf92205bb7..2ec96a616972ba6b8901cd10c2801e207c875bee 100644
--- a/notebooks/2c--Numba.ipynb
+++ b/notebooks/2c--Numba.ipynb
@@ -11,8 +11,6 @@
"# Numba\n",
"**Python for HPC course**\n",
"\n",
- "Sebastian Ohlmann, Klaus Reuter\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -1274,7 +1272,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1288,7 +1286,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.3"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/2d--Diffusion.ipynb b/notebooks/2d--Diffusion.ipynb
index 6d759816e0d5e50e8c16c0adf33b9b6f62106df4..8b98c4b131820165f37a3afac8608fbc40badedd 100644
--- a/notebooks/2d--Diffusion.ipynb
+++ b/notebooks/2d--Diffusion.ipynb
@@ -12,8 +12,6 @@
"\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -4696,8 +4694,8 @@
" grid[ 0, j] = grid[n_points, j] # grid[ 0, j] = grid[-2, j]\n",
" grid[n_points-1, j] = grid[ 1, j] # grid[-1, j] = grid[ 1, j]\n",
" for i in range(n_points + 2):\n",
- " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
- " grid[ i, 0] = grid[ i, n_points-2] # grid[ i, 0] = grid[ i,-2]\n",
+ " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
+ " grid[ i, 0] = grid[ i, n_points] # grid[ i, 0] = grid[ i,-2]\n",
"\n",
"@cython.boundscheck(False) # turn off bounds-checking\n",
"@cython.wraparound(False) # turn off negative index wrapping\n",
@@ -4800,8 +4798,8 @@
" grid[ 0, j] = grid[n_points, j] # grid[ 0, j] = grid[-2, j]\n",
" grid[n_points-1, j] = grid[ 1, j] # grid[-1, j] = grid[ 1, j]\n",
" for i in range(n_points + 2):\n",
- " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
- " grid[ i, 0] = grid[ i, n_points-2] # grid[ i, 0] = grid[ i,-2]\n",
+ " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
+ " grid[ i, 0] = grid[ i, n_points] # grid[ i, 0] = grid[ i,-2]\n",
"\n",
"@cython.boundscheck(False) # turn off bounds-checking\n",
"@cython.wraparound(False) # turn off negative index wrapping\n",
@@ -5015,8 +5013,8 @@
" grid[ 0, j] = grid[n_points, j] # grid[ 0, j] = grid[-2, j]\n",
" grid[n_points-1, j] = grid[ 1, j] # grid[-1, j] = grid[ 1, j]\n",
" for i in range(n_points + 2):\n",
- " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
- " grid[ i, 0] = grid[ i, n_points-2] # grid[ i, 0] = grid[ i,-2]\n",
+ " grid[ i, n_points-1] = grid[ i, 1] # grid[ i,-1] = grid[ i, 1]\n",
+ " grid[ i, 0] = grid[ i, n_points] # grid[ i, 0] = grid[ i,-2]\n",
"\n",
"@cython.boundscheck(False) # turn off bounds-checking\n",
"@cython.wraparound(False) # turn off negative index wrapping\n",
@@ -5517,19 +5515,12 @@
" https://i10git.cs.fau.de/pycodegen/pystencils\n",
"* optional exercise: implement the diffusion computation using pystencils"
]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -5543,7 +5534,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/2e--Interfacing_with_C_and_F.ipynb b/notebooks/2e--Interfacing_with_C_and_F.ipynb
index 33de63179c2c1a25900bc095615b19dad3a71c94..daaba1ad5109353931472b2773b2297e31e2b26a 100644
--- a/notebooks/2e--Interfacing_with_C_and_F.ipynb
+++ b/notebooks/2e--Interfacing_with_C_and_F.ipynb
@@ -10,9 +10,7 @@
"source": [
"# Interfacing Python/NumPy with C/C++ and Fortran Code\n",
"\n",
- "**Python for HPC**\n",
- "\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
+ "**Python for HPC course**\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -444,7 +442,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -458,7 +456,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/3a--Profiling.ipynb b/notebooks/3a--Profiling.ipynb
index 96eca77b29f2320d252d96dba21fe61dbd66e471..912b33addba1c0f11b63f6260840d6ed81e14da6 100644
--- a/notebooks/3a--Profiling.ipynb
+++ b/notebooks/3a--Profiling.ipynb
@@ -11,8 +11,6 @@
"# Profiling\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -23,6 +21,31 @@
"slide_type": "subslide"
}
},
+ "source": [
+ "Argh! My code is very slow. I need to optimize it.\n",
+ "\n",
+ "\n",
+ "But where do I even start? And what does \"slow\" mean? How fast could the code be?"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "I need to analyze my code before I start optimizing. Let's call it \"profiling\"."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "slide"
+ }
+ },
"source": [
"## What is profiling?\n",
"* Profiling: *measure specified performance metrics for different parts of a code*\n",
@@ -47,7 +70,7 @@
"* Profile timing: get list of code parts sorted by the time needed\n",
"* Start optimization\n",
" * Focus on code part taking most time $\\to$ largest benefit\n",
- " * Go through list from top down"
+ "* Profile again and tackle next item on the list"
]
},
{
@@ -557,7 +580,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -571,7 +594,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/3b--Software_Engineering.ipynb b/notebooks/3b--Software_Engineering.ipynb
index 203fbb401c437aad4238d4c3cad7ac37683a02d7..6a452981a5f1efb6343ac1b3acca3c7472587420 100644
--- a/notebooks/3b--Software_Engineering.ipynb
+++ b/notebooks/3b--Software_Engineering.ipynb
@@ -11,7 +11,6 @@
"# Software Engineering\n",
"**Python for HPC course**\n",
"\n",
- "2018-2021 Sebastian Ohlmann, Klaus Reuter\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -55,56 +54,76 @@
},
"source": [
"## Software Packaging\n",
- "* Python provides a standard way of software packaging\n",
+ "* Python provides a standard (but **evolving**) way of software packaging\n",
" * great for \"professional\" software distribution\n",
" * create zipfiles, tarballs, wheel, or egg packages easily\n",
- " * https://packaging.python.org/\n",
- "* `setup.py` using the `distutils` or `setuptools` packages\n",
- " * Information on version, status, authorship, licensing, dependencies\n",
- " * Compilation of Cython, C, Fortran extensions (Makefile replacement)\n",
+ " * metadata specification (version, authorship, license, dependencies, ...)\n",
+ " * Compilation of Cython, C/C++, Fortran extensions (Makefile replacement) (with `setup.py`)\n",
" * Installation to system, per-user, or arbitrary locations\n",
- " * See examples in the folder `setuptools`"
+ " * See examples in the folder `setuptools`\n",
+ " * https://packaging.python.org/"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
- "slide_type": "subslide"
+ "slide_type": "slide"
}
},
"source": [
- "### Example: `setup.py` (see folder `setuptools`)"
+ "### Package configuration: setup.py/pyproject.toml\n",
+ "\n",
+ "* `distutils`/`setuptools` using `setup.py`\n",
+ "* `distutils` is deprecated with removal in python 3.12\n",
+ "* _build-backend_ specification in `pyproject.toml` (PEP517)<br>\n",
+ " $\\to$ enables uses of different backends: `flit`, `hatch`, `pdm`, `poetry`, `setuptools`\n",
+ "* build system isolation (PEP518)\n",
+ "* core metadata specification in `pyproject.toml` (PEP621)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
- "slide_type": "-"
+ "slide_type": "slide"
}
},
"source": [
- "```python\n",
- "from setuptools import setup\n",
- "setup(\n",
- " # name of the software package (as it would appear on PyPI)\n",
- " name=\"helloworld\",\n",
- " version=\"0.1\",\n",
- " # list of the Python modules provided by the package\n",
- " packages=[\"helloworld\"],\n",
- " # list of executable(s) that come with the package (if applicable)\n",
- " scripts=['say_hello.py'],\n",
- " # list of package dependencies (if necessary)\n",
- " #install_requires=['numpy'],\n",
- " # more information, necessary for an upload to PyPI\n",
- " author=\"John Doe\",\n",
- " author_email=\"john.doe@example.mpg.de\",\n",
- " description=\"example package that prints hello world\",\n",
- " license=\"PSF\",\n",
- " keywords=\"hello world example\",\n",
- " url=\"https://example.mpg.de/helloworld/\", # project home page, if any\n",
- ")\n",
+ "### Example: `pyproject.toml` with setuptools (see folder `setuptools`)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "fragment"
+ }
+ },
+ "source": [
+ "```toml\n",
+ "[build-system]\n",
+ "requires = [\"setuptools\"]\n",
+ "build-backend = \"setuptools.build_meta\"\n",
+ "\n",
+ "[project]\n",
+ "name = \"helloworld\"\n",
+ "version = \"0.1\"\n",
+ "# name of the software package (as it would appear on PyPI)\n",
+ "description = \"example package that prints hello world\"\n",
+ "# dependencies = [\"numpy\"]\n",
+ "authors = [\n",
+ " {name = \"John Doe\", email = \"john.doe@example.mpg.de\"}\n",
+ "]\n",
+ "license = {text = \"PSF\"}\n",
+ "keywords = [\"hello\", \"world\", \"example\"]\n",
+ "\n",
+ "[project.urls]\n",
+ "homepage = \"https://example.mpg.de/helloworld/\"\n",
+ "\n",
+ "# list of executable(s) that come with the package (if applicable)\n",
+ "[project.scripts]\n",
+ "hello-world = \"helloworld.cli:hello_world\"\n",
"```"
]
},
@@ -116,14 +135,14 @@
}
},
"source": [
- "### Usage of setup.py\n",
- "* Install package with `python setup.py install --user`<br>\n",
- " $\\to$ installation path under `~/.local/lib/...`\n",
- "* This will make the package available for your local user\n",
- "* Build package including extensions with `python setup.py build`\n",
+ "### Installing and distributing packages\n",
+ "* Install package with `pip install .`<br>\n",
+ " add `--user` $\\to$ installation path under `~/.local/lib/...`;<br>\n",
+ " this will make the package available for your local user\n",
+ "* Build package including extensions with `python -m build`\n",
"* Create distribution packages for sharing\n",
- " * Source package with `python setup.py sdist`\n",
- " * Binary package with `python setup.py bdist`"
+ " * Source package with `python -m build --sdist`\n",
+ " * Binary package with `python -m build --wheel`"
]
},
{
@@ -134,17 +153,40 @@
}
},
"source": [
- "### Advantages of using `setup.py`\n",
+ "### Advantages of using python-packaging\n",
"\n",
"* Easy package installation to arbitrary locations\n",
"* Better handling of different versions\n",
"* Easy integration of extensions (Cython, C, C++, Fortran)\n",
- "* For development: use `pip install -e ./ --user` (development install, always uses the modules from the current folder)\n",
+ "* For development: use `pip install -e .` (development install, always uses the modules from the current folder)<br>\n",
+ " depending on the pip-version (`<v21.1`), a dummy `setup.py` is necessary\n",
"* Facilitates sharing of the code with others, potentially via PyPI\n",
"\n",
"$\\to$ recommended for all projects!"
]
},
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "### Folder structure of a python package\n",
+ "\n",
+ "```\n",
+ "project_root_directory\n",
+ " pyproject.toml\n",
+ " package_name/ # folder of the package\n",
+ " __init__.py # initialize the package\n",
+ " module_a.py # some python module\n",
+ " module_b.py # some other module\n",
+ "```\n",
+ "* can be autodetected with `setuptools`\n",
+ "* can be imported with `import package_name` or `from package_name import module_a`"
+ ]
+ },
{
"cell_type": "markdown",
"metadata": {
@@ -156,7 +198,7 @@
"### Components of a full-fledged software package\n",
"\n",
"* source code\n",
- "* installation routines (`setup.py`)\n",
+ "* package metadata and specification of extensions (`pyproject.toml` and `setup.py` in case)\n",
"* user documentation - how to use the package\n",
"* developer documentation - how to develop code for the package\n",
"* software tests\n",
@@ -167,6 +209,19 @@
" * `CHANGELOG`"
]
},
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "slideshow": {
+ "slide_type": "subslide"
+ }
+ },
+ "source": [
+ "### Further reading:\n",
+ "* https://packaging.python.org/\n",
+ "* https://setuptools.pypa.io/"
+ ]
+ },
{
"cell_type": "markdown",
"metadata": {
@@ -298,15 +353,15 @@
"Steps\n",
"\n",
"* Use `sphinx-quickstart` to create default files for the documentation\n",
- "* Adapt `conf.py` to your needs, enable useful Sphinx addons such as\n",
+ "* Adapt `doc/conf.py` to your needs, enable useful Sphinx addons such as\n",
" * `sphinx.ext.autodoc`: include docstrings into documentation\n",
" * `sphinx.ext.napoleon`: support for NumPy-style docstrings\n",
- "* Edit `index.rst`, potentially create other rst files\n",
- "* Run `make html` to generate the HTML documentation\n",
+ "* Edit `doc/index.rst`, potentially create other rst files\n",
+ "* Run `cd doc && make html` to generate the HTML documentation<br>\n",
+ " or run `sphinx-build -b html <source-dir> <out-dir>`\n",
"\n",
"Example\n",
"\n",
- "* Can be integrated into `setup.py` (run ` python setup.py build_sphinx`)\n",
"* See the directory `setuptools/sphinx-doc` for an example"
]
},
@@ -410,7 +465,7 @@
"```yaml\n",
"test-python:\n",
" script:\n",
- " - python setup.py pytest\n",
+ " - pytest -v\n",
"```\n",
"* This will run the tests on every push event\n",
"* Uses shared runners to execute the tests $\\to$ for special needs, separate runners can be used\n",
@@ -430,7 +485,7 @@
"* https://pypi.python.org/pypi\n",
"* Contains nearly 330.000 packages (Oct 2021)\n",
"* Zip files, tar balls, wheel archives are accepted \n",
- " (typically generated locally by `setup.py` first)\n",
+ " (typically generated locally by `setup.py`/`python -m build` first)\n",
"* Anybody may upload packages after registration"
]
},
@@ -468,7 +523,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -482,7 +537,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.3"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/4a--Parallel_Programming.ipynb b/notebooks/4a--Parallel_Programming.ipynb
index 8690043d2c1f59bc0e5e0f8672228a627d1da6ca..c205077074757cd2f8b3973f37c72dcf30ec3657 100644
--- a/notebooks/4a--Parallel_Programming.ipynb
+++ b/notebooks/4a--Parallel_Programming.ipynb
@@ -11,8 +11,6 @@
"# Parallel programming\n",
"**Python for HPC course**\n",
"\n",
- "Sebastian Ohlmann, Klaus Reuter\n",
- "\n",
"Max Planck Computing and Data Facility, Garching"
]
},
@@ -239,9 +237,6 @@
"* Shared memory: all processes/threads can access the same memory $\\to$ only on one node\n",
" * Threads: **OpenMP** for C and Fortran\n",
" * Processes: `multiprocessing` for Python\n",
- " * Shared-memory programming models\n",
- " * Fork-join\n",
- " * Task based\n",
"* Distributed memory: each process has its own memory $\\to$ may cover several nodes\n",
" * **MPI**: message passing interface\n",
" * Communication handled by programmer\n",
@@ -322,9 +317,7 @@
"* Idea: Start several processes on one node to distribute the workload over CPUs\n",
"* Use processes instead of threads $\\to$ sidestep the global interpreter lock\n",
"* `multiprocessing` module, part of the Python standard library\n",
- "* 2 important use cases:\n",
- " * Data parallelism with the `Pool` class (*fork-join model*)\n",
- " * Task parallelism with `Process` class and task queues (*task-based model*)"
+ "* Most important use case: Data parallelism with the `Pool` class"
]
},
{
@@ -409,58 +402,6 @@
"print(result)"
]
},
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### `multiprocessing.Pool` $-$ processes"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "process 32110 squares -1\n",
- "process 6507 squares 1process 6506 squares 0process 6508 squares 2\n",
- "process 6508 squares 3\n",
- "process 6506 squares 4\n",
- "process 6506 squares 5\n",
- "\n",
- "\n",
- "[0, 1, 4, 9, 16, 25]\n"
- ]
- }
- ],
- "source": [
- "from multiprocessing import Pool\n",
- "import os\n",
- "\n",
- "def f(x):\n",
- " sq = x*x\n",
- " print(\"process {} squares {}\".format(os.getpid(), x))\n",
- " return sq\n",
- "\n",
- "f(-1)\n",
- "with Pool(3) as p:\n",
- " result = p.map(f, range(6))\n",
- "\n",
- "# There are really different processes (process IDs)!\n",
- "print(result)"
- ]
- },
{
"cell_type": "markdown",
"metadata": {
@@ -508,217 +449,6 @@
"print(\"pool time: {:f}\".format(time.time() - start))"
]
},
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### `multiprocessing.Process`\n",
- "* Process objects can be created individually to implement more complex parallel patterns\n",
- "* Subprocess is forked with the `start()` function $\\to$ generates child process\n",
- "* Entry point (function to be executed) given via the target parameter"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 21,
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "Hello Alice from pid 3478\n",
- "Hello Bob from pid 11837\n",
- "False\n"
- ]
- }
- ],
- "source": [
- "from multiprocessing import Process\n",
- "import os\n",
- "\n",
- "def info(s):\n",
- " print('Hello {} from pid {}'.format(s, os.getpid()))\n",
- "\n",
- "info('Alice')\n",
- "\n",
- "p = Process(target=info, args=('Bob',))\n",
- "\n",
- "p.start()\n",
- "p.join()\n",
- "\n",
- "#p.terminate()\n",
- "\n",
- "print(p.is_alive())"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### `multiprocessing.Queue`\n",
- "* Enables communication between processes\n",
- "* Handled transparently in the background\n",
- "* Any `pickle`'able object can be passed between processes"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "Hello parent process!\n"
- ]
- }
- ],
- "source": [
- "from multiprocessing import Process, Queue\n",
- "\n",
- "def f(q):\n",
- " q.put(\"Hello\")\n",
- " q.put(\"parent\")\n",
- " q.put(\"process!\")\n",
- "\n",
- "q = Queue()\n",
- "p = Process(target=f, args=(q,))\n",
- "\n",
- "p.start()\n",
- "print(q.get(), q.get(), q.get())\n",
- "p.join()\n",
- "print(q.get(), q.get(), q.get())"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### More on `multiprocessing.Queue`\n",
- "\n",
- "* Multiple processes may share the same queue\n",
- "* Several queues per process are possible\n",
- "* Results can be retrieved, e.g., at the parent process\n",
- "* Enables to implement, e.g. parallel producer-consumer-pattern easily"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 37,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "[0, 0]\n",
- "[1, 1]\n",
- "[2, 4]\n"
- ]
- }
- ],
- "source": [
- "from multiprocessing import Process, Queue\n",
- "\n",
- "def f(i, q):\n",
- " q.put([i, i**2])\n",
- "\n",
- "q = Queue()\n",
- "ps = []\n",
- "num_proc = 3\n",
- "for i in range(num_proc):\n",
- " ps.append(Process(target=f, args=(i, q)))\n",
- "# start processes\n",
- "for p in ps:\n",
- " p.start()\n",
- "# get results\n",
- "for i in range(num_proc):\n",
- " print(q.get())\n",
- "# join processes\n",
- "for p in ps:\n",
- " p.join()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### More on `multiprocessing.Queue`\n",
- "\n",
- "* using `iter()`, it is possible to iterate over the elements in a queue\n",
- "* `iter()` supports a sentinel that can be used to implement a stop signal\n",
- "* useful if number of processes not the same as number of elements in the queue\n",
- "* in practice, set timeouts and number of max items in queue explicitly for your setup"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 22,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "Process 0 does 0Process 1 does 1\n",
- "\n",
- "Process 0 does 3\n",
- "Process 1 does 2\n",
- "Process 0 does 4\n"
- ]
- }
- ],
- "source": [
- "from multiprocessing import Process, Queue\n",
- "\n",
- "def f(i, q):\n",
- " for j in iter(q.get, 'STOP'):\n",
- " print(\"Process {:d} does {}\".format(i, j))\n",
- "\n",
- "q = Queue()\n",
- "num_proc = 2\n",
- "ps = [Process(target=f, args=(i, q)) for i in range(num_proc)]\n",
- "# start processes\n",
- "for p in ps:\n",
- " p.start()\n",
- "# put work into queue\n",
- "num_elements = 5\n",
- "for i in range(num_elements):\n",
- " q.put(i)\n",
- "# send stop signal to all processes\n",
- "for i in range(num_proc):\n",
- " q.put('STOP')\n",
- "# join processes\n",
- "for p in ps:\n",
- " p.join()"
- ]
- },
{
"cell_type": "markdown",
"metadata": {
@@ -732,15 +462,12 @@
"* Python threads are not useful for HPC\n",
"* Processes can be used with `multiprocessing` module\n",
"* Simple cases of data parallelism $\\to$ `Pool` class with fork-join model\n",
- "* More complex cases, functional, or task parallelism \n",
- " $\\to$ `Process` class with communication via `Queue`\n",
"* Creating processes is expensive $\\to$ work packages for each process should be large enough!\n",
"\n",
"### Outlook: multiprocessing exercises\n",
"\n",
"* Parallel image processing\n",
- "* Monte Carlo $\\pi$ computation\n",
- "* Work-queue system"
+ "* Monte Carlo $\\pi$ computation\n"
]
},
{
@@ -762,7 +489,8 @@
" * Peer-to-peer communication\n",
"* Various implementations are available, e.g.\n",
" * OpenMPI (via Linux distributions)\n",
- " * IntelMPI (commercial product, on HPC systems)"
+ " * IntelMPI (commercial product, on HPC systems)\n",
+ " * and many others"
]
},
{
@@ -1145,11 +873,9 @@
"```python\n",
"sendbuf = None\n",
"if rank == 0:\n",
- " sendbuf = np.empty([size, 100], dtype='i')\n",
- " sendbuf.T[:,:] = range(size)\n",
- "recvbuf = np.empty(100, dtype='i')\n",
+ " sendbuf = np.arange(size*4, dtype='i')\n",
+ "recvbuf = np.empty(4, dtype='i')\n",
"comm.Scatter(sendbuf, recvbuf, root=0)\n",
- "assert np.allclose(recvbuf, rank)\n",
"```"
]
},
@@ -1806,8 +1532,7 @@
"## Summary: parallel programming with python\n",
"\n",
"* **Shared-memory programming** with processes: `multiprocessing` module\n",
- " * Use `Pool` class for easier problems\n",
- " * Advanced usage: `Process` class, task queues\n",
+ " * Use `Pool` class for simple parallelization schemes\n",
" * *Use on one node only*\n",
"* **Distributed-memory programming** with MPI: `mpi4py` module\n",
" * Provides wrappers around all MPI-1/2/3 functions\n",
@@ -1912,306 +1637,12 @@
"\n",
"**python for HPC**: fast development of code + high performance is possible!"
]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Additional material"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Application example: Parallel decorators\n",
- "\n",
- "* Open source project started a few years ago\n",
- "* Goal: postprocess hundreds of simulation snapshots (e.g., create a figure) $\\to$ embarassingly parallel\n",
- "* Problem: postprocessing loop over snapshots takes very long\n",
- "* How to parallelize this easily?\n",
- "* One way: use `parallel_decorators`"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Example\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "```python\n",
- "# Original code\n",
- "results = np.zeros(number_snapshots)\n",
- "for index in range(number_snapshots):\n",
- " snapshot = open_snapshot(index)\n",
- " results[index] = compute_something_difficult(snapshot)\n",
- " save_some_figure()\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "fragment"
- }
- },
- "source": [
- "rewrite as:"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "```python\n",
- "# as function\n",
- "def postprocess_snapshot(index):\n",
- " snapshot = open_snapshot(index)\n",
- " result = compute_something_difficult(snapshot)\n",
- " save_some_figure()\n",
- " return result\n",
- "\n",
- "results = [postprocess_snapshot(index) for index in range(number_snapshots)]\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Using parallel decorators\n",
- "Reuse approach with function:"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "```python\n",
- "from parallel_decorators import vectorize_parallel\n",
- "\n",
- "#@vectorize_parallel(method='MPI')\n",
- "@vectorize_parallel(method='processes', num_procs=2)\n",
- "def postprocess_snapshot(index):\n",
- " # function body same as before\n",
- " snapshot = open_snapshot(index)\n",
- " result = compute_something_difficult(snapshot)\n",
- " save_some_figure()\n",
- " return result\n",
- "\n",
- "results = postprocess_snapshot(range(number_snapshots))\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Parallel decorators\n",
- "\n",
- "* Easy approach to parallelize a range of long tasks\n",
- "* Rewrite loops to function, add decorator\n",
- "* Parallelization using multiprocessing or mpi4py\n",
- "* Available at https://github.com/ohlmann/parallel_decorators"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Application example: Sparse Matrix-Vector product\n",
- "* Background: time evolution of quantum state\n",
- "* Goal: compute $y = M x$, where $M$ is a $N\\times N$ matrix and $x$ and $y$ are vectors\n",
- "* $N$ can be huge ($10^9$)\n",
- "* $M$ is very sparse (about 25 elements per row)\n",
- "* Strategy:\n",
- " * distribute rows of matrix and vectors over processors (static distribution)\n",
- " * compute rows of $y$ by local sparse matrix-vector product\n",
- " * rows of $x$ corresponding to columns of $M$ needed $\\to$ communication\n",
- " * use block domain decomposition to ensure good locality\n",
- " * modify existing serial code minimally invasive"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Matrix-Vector product: data decomposition\n",
- "* Distribution of matrix generation and multiplication needed\n",
- "* $M$ is built from Kronecker products $M = A \\otimes B$\n",
- "* Distribute this product over rows of $A$: $M_j = A_j \\otimes B$ on processor $j$\n",
- "* Here, $A_j$ contains rows from $\\lfloor jN_A/p\\rfloor$ to $\\lfloor (j+1)N_A/p\\rfloor -1$\n",
- "* Thus, $M_j$ contains rows from $\\lfloor jN_A/p\\rfloor N_B$ to $\\lfloor (j+1)N_A/p\\rfloor N_B -1$\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "```python\n",
- "import numpy as np\n",
- "from mpi4py import MPI\n",
- "\n",
- "def get_decomposition(NA, NB):\n",
- " comm = MPI.COMM_WORLD\n",
- " rank = comm.Get_rank()\n",
- " nproc = comm.Get_size()\n",
- " # get block domain decomposition\n",
- " edges = np.arange(nproc + 1) * NA // nproc * NB\n",
- " # sizes on all cores\n",
- " sizes = np.diff(edges)\n",
- " # bounds on this core\n",
- " bounds = (edges[rank], edges[rank+1])\n",
- " return edges, sizes, bounds\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Distribution of generation"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "```python\n",
- "def distributed_kron(A, B):\n",
- " comm = MPI.COMM_WORLD\n",
- " rank = comm.Get_rank()\n",
- " size = comm.Get_size()\n",
- " N = A.shape[0]\n",
- " rowmin = rank * N // size\n",
- " rowmax = (rank + 1) * N // size\n",
- " return kron(A, B, rowrange=(rowmin, rowmax))\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Distribution of product\n",
- "1. determine communication pattern once ($M$ is constant) $\\to$ use `Alltoall`\n",
- "2. communicate needed vector rows from neighbours $\\to$ use `Alltoallv` because number of communicated elements is different on each core\n",
- "3. compute sparse product"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "```python\n",
- "def sparse_product(M, vec):\n",
- " large_vec = get_vec_from_neighbours(M, vec)\n",
- " return M.dot(large_vec)\n",
- "\n",
- "def get_vec_from_neighbours(M, vec):\n",
- " comm = MPI.COMM_WORLD\n",
- " large_vec = np.zeros(M.num_cols, dtype=np.float64)\n",
- " # vector_rows_needed: indices of needed rows of vec\n",
- " data_rcv = np.zeros_like(M.vector_rows_needed, dtype=np.float64)\n",
- "\n",
- " data_snd = vec[M.rows_snd]\n",
- " # each argument: buffer, number of elements to send/receive on this rank,\n",
- " # offsets for sending/receiving on all ranks, datatype\n",
- " comm.Alltoallv([data_snd, M.num_snd, M.offset_snd, MPI.DOUBLE],\n",
- " [data_rcv, M.num_rcv, M.offset_rcv, MPI.DOUBLE])\n",
- " large_vec[M.vector_rows_needed] = data_rcv[:]\n",
- "\n",
- " return large_vec\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Lessons from this example\n",
- "* `mpi4py` offers easy-to use MPI wrappers also for complex communication patterns\n",
- "* enables scaling to problem sizes not feasible on a single node\n",
- "* scaling tested up to $N~2\\times 10^9$ on up to 1024 cores\n",
- "* combines power of distributed computing with ease of development in python\n",
- "* usually, the parallel part can be encapsulated in a few functions"
- ]
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -2225,7 +1656,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.8"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/5a--Visualization.ipynb b/notebooks/5a--Visualization.ipynb
index b0e2d7cc1672a540b765cbd06301720695575d7b..5882ee6f4b3349988557eedc7122b3a261501cdb 100644
--- a/notebooks/5a--Visualization.ipynb
+++ b/notebooks/5a--Visualization.ipynb
@@ -11,7 +11,6 @@
"# Visualization\n",
"**Python for HPC course**\n",
"\n",
- "Sebastian Ohlmann, Klaus Reuter\n",
"\n",
"Max Planck Computing and Data Facility, Garching"
]
@@ -31,7 +30,7 @@
"* Here:\n",
" * Matplotlib\n",
" * Some examples\n",
- " * Some words on color scales"
+ " * Some words on colors"
]
},
{
@@ -330,7 +329,7 @@
" * *sequential* colormaps (monotonous change in lightness) for ordered data\n",
" * *diverging* colormaps (two different colors meet in middle) for data deviating from a mean value\n",
" * *qualitative* colormaps for information without ordering/relationships (e.g. different lines in line plots)\n",
- " * **avoid** the jet colorscale\n",
+ " * **avoid** the jet or rainbow colorscale\n",
"* [matplotlib colormaps](https://matplotlib.org/tutorials/colors/colormaps.html)"
]
},
@@ -1279,7 +1278,7 @@
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
- "display_name": "Python 3",
+ "display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
@@ -1293,7 +1292,7 @@
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
- "version": "3.8.3"
+ "version": "3.9.7"
}
},
"nbformat": 4,
diff --git a/notebooks/5b--Visualization_part2.ipynb b/notebooks/5b--Visualization_part2.ipynb
deleted file mode 100644
index 79f3750643feb1d589db4dfb0f6505b30bea6f6c..0000000000000000000000000000000000000000
--- a/notebooks/5b--Visualization_part2.ipynb
+++ /dev/null
@@ -1,1374 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "# Visualization with Python, Part 2\n",
- "## César Allande\n",
- "## Max Planck Computing and Data Facility, Garching"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Outline\n",
- "\n",
- "1. Introdution\n",
- "0. First plots\n",
- " - Different types of plots\n",
- " - How to decorate\n",
- "0. Multi plot\n",
- " - Multiplot arrangement\n",
- "0. Extension - other packages\n",
- " \n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Introduction\n",
- "\n",
- "[**Matplotlib**][1] is a plotting library for the Python programming language.\n",
- "- Object oriented API\n",
- "\n",
- "> Provides a quick way to visualize data from Python and publication-quality figures in many formats.\n",
- "\n",
- "[**Pyplot**][2] is a matplotlib module that provides an interface to the matplotlib object-oriented plotting library.\n",
- "\n",
- "> Easy transition from Matlab. Majority of comands are analog to the Matlab interface\n",
- "\n",
- "[1]: https://matplotlib.org/\n",
- "\n",
- "[2]: https://matplotlib.org/tutorials/introductory/pyplot.html\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "A [**Figure**][1] is the windows in the GUI space. \n",
- "\n",
- "[**Axes**][2] is the container of the figure elements: Axis, Tick, Line2D, Text, etc.\n",
- " \n",
- "[**Axis**][3] corresponds to the axis properties of an Axes (x,y,z)\n",
- "\n",
- "\n",
- "[1]: https://matplotlib.org/api/_as_gen/matplotlib.figure.Figure.html#matplotlib.figure.Figure\n",
- "\n",
- "[2]: https://matplotlib.org/api/axes_api.html\n",
- "\n",
- "[3]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.axis.html\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "source": [
- "> Every Axes corresponds to only one Figure, but a Figure can contain multiple Axes. This allows to create subplots in a Figure\n",
- "\n",
- "\n",
- "<img src=\"./fig/vis_fig_map.png\" style=\"width: 400px;\" />"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Types of plots\n",
- "\n",
- "- Lines : [**plot()**][4]\n",
- "\n",
- "- Scatter: [**scatter()**][5]\n",
- "\n",
- "- Histograms: [**hist()**][6]\n",
- "\n",
- "- Bar charts: **bar()**\n",
- "- Log plots: **semilogx(), semilogy(), loglog()**\n",
- "- Pie charts: **pie()**\n",
- "- ... \n",
- "\n",
- "\n",
- "[4]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html?highlight=plot#matplotlib.pyplot.plot\n",
- "\n",
- "[5]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.scatter.html?highlight=scatter#matplotlib.pyplot.scatter\n",
- "\n",
- "[6]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.hist.html?highlight=hist#matplotlib.pyplot.hist\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "\n",
- "# First plots \n",
- "\n",
- "- Basic plot with lines\n",
- "- Lines, adjustement of properties\n",
- "- Scatter\n",
- "- Histogram\n",
- "- Stacked\n",
- "- Stacked, decoration\n",
- "- Combined plot and decoration\n",
- "- 3D Surface\n",
- "- Heatmap\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Basic Lines: plot()\n",
- "\n",
- "Data can be passed in different ways\n",
- "- Multiple times call\n",
- "- Multiple sets \n",
- "- Passed through 2D arrays"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 217,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD7CAYAAACRxdTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3XdcVvX///HHG/dCRXEP3IrixL1z4DbUyiz3tj6OvqU0LHNrhqMcWbbLTHFvc4DiSLQEJPdMRVBUEGS/f38c/H34kAkocK7r4nW/3brd4LoOnOe5Xfnidb2vc15Haa0RQghhW+zMDiCEECLjSXEXQggbJMVdCCFskBR3IYSwQVLchRDCBklxF0IIGyTFXQghbJAUdyGEsEFS3IUQwgblNGvHxYsX105OTmbtXgghrNKJEyfuaK0dU9vOtOLu5OSEn5+fWbsXQgirpJS6mpbtZFlGCCFskBR3IYSwQVLchRDCBklxF0IIGyTFXQghbFCaz5ZRSuUDjgG7tdZvp3jODpgNPAQqAqu01kczMqgQQoi0S8+pkDOBP/7luZcBe621h1LKATiqlKqltU547oRCCCHSLU3LMkqpgYAvcPlfNukOHAHQWocB0UDtjAj4D5F3YOe7EP0gU369EEJklriERJYduMCp6/czfV+pFnellDNQS2u9/imblQAikn0fnvRYyt81Sinlp5TyCw0NTXdYAC4dgGMrYGlTOLvj2X6HEEJkscAbD3hxqS/zd55lR2Bwpu8vLZ27OxCtlPIAWgFNlFITU2wTAhRK9r190mP/Q2u9UmvtqrV2dXRM9erZJ3PpByN+g3wOsLo/rBtudPNCCGGBouMS+GTXGXov9eV2eAzLX2uIR9eamb7fVNfctdazHn+tlMoLFNRaL1JKFQDya61DgW1AG+CHpDX3vMDpTMoMZRvBqANwaCH4fAIX90HX+UbhVyrTdiuEEOnhdyWMyV7+XAqN5KVG5figuzOF8+fKkn2n52yZvhgFPLdS6lXAAXABxgC/Ag2UUh8BFYBBmf5has7c0G4KOPeCTW/C+hEQsBZ6eELhcpm6ayGEeJqHMfF8svMM3x+9SpnC+fh+WBPaVH/G1YpnpLTWWbrDx1xdXXWGDQ5LTDDW4ffOALuc0Hk6NBwCdnIavxAia3mfC+W99QHcfPCIwc2deMetBgXyZNyMRqXUCa21a2rbmTYVMkPZ5YDmb0CNbrBlPGydBAFe0GsJFKtidjohRDZwPyqWGVv/wuvk31RxLMDa0c1xdXIwLY9ttbYOlWDQZuj1GQQHwPIW4LsEEuLNTiaEsGE7Am7R0dOHTX/e4M32Vdk2vrWphR1spXNPTiloOAiqdoJt/wd7psLp9dDrcyhVx+x0QggbEhIezYebTrPzdDB1ytrz3bDG1C5T2OxYgK117snZl4b+P0G/b+D+dVjZFvbNgvgYs5MJIayc1ppf/a7T0dObfWdDmNKlJhvHtbSYwg622LknpxTU6QOV28FOD/CZD39tNrr48o3NTieEsELXw6J4b0MAB8/foYmTA3P7ulDZsaDZsf7Bdjv35PI7QJ+VMGAtxETAqk7GCIPYSLOTCSGsREKi5hvfy7gt8uHk1XvM6F2bX0Y1s8jCDrbeuadUvTOMOwp7P4ajy+DMNuOMmsrtzE4mhLBgF0IimOIVwImr92hXw5FZ7i6ULZLP7FhPlT069+Ty2kP3T2HIduOc+O97GxdBPcr8QT5CCOsSl5DI5/vO023xIS6GPmThK/X4Zkhjiy/skN069+ScWsJYXzgwFw5/Buf3GEW/Vg+zkwkhLEDA3w94Z90pzgRH0L1uaT7uVZviBfOYHSvNsl/nnlyufNDpYxi5Fwo4wprX4NfB8PAfM8+EENlEdFwCc3ec4cVlvoRFxvLFwEYsHdDQqgo7ZOfOPbkyDWDUfvBdBN7z4bI3dJkLdV+RQWRCZCPHLt3FY30Al+9E8opred7rXovC+bJm0FdGy96de3I5ckGbd2DMIShWDTaMhp9eMs6RF0LYtIjoOKZuDOSVlUeJT0zkpxFNmdevrtUWdpDi/k+ONWDYTmOE8NXDsKwZ/P4lJCaanUwIkQn2nwnBbaEPPx67yvBWldg1sQ0tqxY3O9Zzk2WZJ7HLAU1HQ/UusGUCbH8bAtcbp00Wr2Z2OiFEBgiLjGXG1iA2/HGDaiUK4jW2BQ0rFDU7VoaRzv1pilaEgRug9zIIOQ3LW8JBTxlEJoQV01qz1f8mnTy92XLqJuM7VGPr+FY2VdhBOvfUKQUNXoOqHYxBZHs/hqCNxgiD0nXNTieESIfb4dF8sDGQPUG3qVuuMD+OaEqt0vZmx8oU0rmnVaFSxiCyl7+H8Fuwsh3snQ5x0WYnE0KkQmvNmuPX6Ojpjc+5UN7rVpP1Y1vYbGEH6dzTz7k3OLWGXe/DwU/hry1GF1+hqdnJhBBPcO1uFB7r/Tl88S5NKzkwr29dnIoXMDtWppPO/VnkdwD35fC6F8Q9gq/dYPtkiHlodjIhRJKERM1XBy/ReZE3/n8/YLa7C6tHNssWhR2kc38+VTvCuCPG8szvK+HsDui5yFifF0KY5tztCCav8+fP6/d5oWYJZrnXoXRhy58Hk5Gkc39eeQpBt09g6A7ImQd+7AMbx0FUmNnJhMh2YuMTWfzbebovOci1sCgW96/PqsGu2a6wg3TuGadic+PqVp/5cGhR0iCyBcYavRAi0526fp8pXv6cCY6gd/0yfNjDmWJWNg8mI0nnnpFy5YUOH8KoA8bZNb8OgjUDIeK22cmEsFmPYhOYvf0v3Jf5cj8qjq8GubK4f4NsXdhBOvfMUboujNxnjBI+MBcu+4DbbKg/QAaRCZGBjly8i8d6f67ejWJA0wp4dK2JfV7rnQeTkaRzzyw5ckHrt4yZ8SVqwaZxxnr8vatmJxPC6oVHx/Hu+gBe/fIoAD+PbMpsdxcp7Mmk2rkrpeyALcAxIDdQBRimtX6UbJshwBjg8RU9q7TWP2R4WmtUvJpx1ye/VfDbNFjWHDp+BI1Hgp38bRUivfb+dZv3NwQSEhHNqDaVmdSxOvly5zA7lsVJ67LMEa31TACl1CagD/BTim36a62vZGA222FnB01GQnU32DoJdkyGQC/o9ZkxhVIIkaq7D2P4eEsQm0/dpGapQnwxsBH1yhcxO5bFSrW4a60TgceFPSdQDjj7hE3fVEoFA/mBz7XWci5gSkUqwGvrwH8N7PSAFa2g7RRoOcFYxhFC/IPWms2nbvLxliAiouOY1LE6Y9tVIXdOeef7NEprnbYNlXIDJgHHtNYfpXiuEvBQax2qlOoG/J/W+h9X8iilRgGjACpUqNDo6tVsvP78MAS2v2MMISvlYowwKFPf7FRCWJRbDx7xwYZA9p4JoX75IszvV5fqJQuZHctUSqkTWmvXVLdLa3FP9ou/B45qrZf9y/N5gYdAHq11wr/9HldXV+3n55eufdukv7YY0yYj70DL8UYnnyv7XXAhRHKJiZrVx68xZ/sZ4hMTebtzDYa2rEQOOznbLK3FPdX3NUopZ6VU92QPXQYqK6UclFL2SdvMSVqyAagGXH5aYRfJ1OoJbxyD+q/CoYXGUs3Vw2anEsI0V+5EMuCro7y/IZC65Qqze2JbRrSuLIU9ndLygWoMMFwp1QDIBdQCxgMeQBgwFwgGliulLgMuwMDMiWuj8hWF3kuhTj/YMh6+6QqNR0DHacZ4AyGygfiERL72vcynu8+RO6cd8/q68LJreZRcG/JM0r0sk1FkWeZfxEbCvplwdDnYlzUGkVXrZHYqITLVmeBwpqzz59TfD+jkXJKZL9ahpH1es2NZpAxblhFZLHcB6DIHhu82vv6pH6wfLYPIhE2KiU/Ac885eiw5xN/3HvH5gAasHNhICnsGkPEDlqp8ExhzEHwWwCFPuLjXmD7p/KKMMBA24eS1e0xZ58/5kIe4NyjLhz2cKVogt9mxbIZ07pYsZx544X1jEJl9WVg7BNa8btzmTwgrFRUbz4ytQfRdfpiHMfF8M6QxC1+pL4U9g0nnbg1KucCIvXB0KeyfDUubgttMaDBQunhhVXwv3MFjvT/Xwx4xsFlFJnepQSGZB5MppHO3FjlyGleyjj0MperA5v/A970h7LLZyYRI1YNHcXh4+fPaV8fIaWfHmlHNmPFiHSnsmUiKu7UpVgUGb4XunnDjJCxvAUeWQaJcViAs0+7TwXTy9Gbtib8Z07YKOya0pmnlYmbHsnmyLGON7Oyg8fD/DiLb9S6cXm+MMChR0+x0QgAQGhHDtC2n2eZ/i1ql7Vk1uDEu5QqbHSvbkM7dmhUuBwN+hT5fwt2L8EVr8J4P8bFmJxPZmNaaDX/8TaeF3uw5fZu3O1dn85stpbBnMencrZ1SUPdlqNwedk6B/bMgaJMxTrhsQ7PTiWzmxv1HvL8hgANnQ2lYwRj0VbWEXGVtBuncbUVBR+j3NfRfDVF34asOsHsqxEaZnUxkA4mJmh+OXKGzpzfHLoXxUU9n1o5pIYXdRNK525qa3cCppVHYDy+BM1uNLt6pldnJhI26FPoQD68Afr8SRutqxZnt7kJ5h/xmx8r2pHO3RXkLQ68lMGgz6ET4trvxwWt0uNnJhA2JT0hk+YGLdFl8kDPB4XzSry7fD2sihd1CSOduyyq3hbFHjHX4o8vg3C7osdA4y0aI5xB0M5zJXqcIvBGOW+2SzOhdhxIyD8aiSOdu63LnB7dZMHwP5LGHn18GrxHGzUGESKfouAQW7DpLr88PEfwghuWvNeSLga5S2C2QdO7ZRTlXGO1jDCHzWQAX90HX+VCnr4wwEGly4moYk9f5czE0kr4NyzG1Ry2K5Jd5MJZKOvfsJGduaOdhFPmiTuA1HFa/CuE3zU4mLFhkTDzTNp+m34ojRMcl8t2wJnz6cj0p7BZOint2VNLZWKbpPAsuHTAGkZ34Fky6cYuwXD7nQum80IfvjlxhULOK7JrUhrbVHc2OJdJAint2ZZcDWrwJ4w5D6XqwZQJ81xPCLpmdTFiAB1FxvL32FIO+/p08uez4dXRzPu5dh4J5ZCXXWkhxz+4cKsPgLdBzMdw6BctawOHPZRBZNrYz8BYdF3qz4Y8bjGtXhe3jW9PYycHsWCKd5M+wMD5QbTQEqnWGrW/B7vf/O4ispLPZ6UQWCYmI5qNNp9kRGEztMvZ8M6QxdcrKPBhrJZ27+C/7MvDqamOMwb2r8EUb2D9HBpHZOK016078TSdPH/aeCWFylxpsfKOlFHYrJ527+F9KGadHVmoHOz3Ae64xiKz3UijXyOx0IoNdD4vivQ0BHDx/h8ZORZnbty5VHAuaHUtkAOncxZMVKAZ9vzRGCseEw6qOsOt9GURmIxITNd/6XsZtkQ8nr95jeu/arBnVXAq7DZHOXTxddTcYdxR++wiOfP7fQWSV2pidTDyjCyEP8fDyx+/qPdpUd2S2ex3KFZV5MLZGOneRurz2xkyaIdtA2RmnTG4eD4/um51MpENcQiJL91+g2+KDXAh9yKcv1eO7oY2lsNuoVDt3pZQdsAU4BuQGqgDDtNaPkm2TF1gA3ACqAXO11ucyJbEwj1Mr4wbdB+bA4c/g/G7jXq41u5mdTKQi8MYDJq/zJ+hWON1dSjOtV20cC+UxO5bIRGnt3I9oradrrT8A8gN9Ujw/EbimtZ4DLARWZWBGYUly5YNO02HEXsjnAL+8CmuHwsNQs5OJJ4iOS2DezjP0XupL6MMYVrzeiKWvNZTCng2kWty11ola65kASqmcQDngbIrNugNHkrYPAOoppewzOKuwJGUbwqgD0P4DYx1+aRPw/1VGGFiQ41fC6Lb4IMsPXKRvw7L8NqktXeqUMjuWyCJpXnNXSrkBW4GtWmu/FE+XACKSfR+e9FjK3zFKKeWnlPILDZVOz+rlzA1t34HRB6FYFVg/En5+BR78bXaybO1hTDwfbgrkpRVHiE1I5MfhTZnfrx6F8+cyO5rIQkqns9NSSn0PHNVaL0v22EHgPa31waTvw4FyWut/vfWPq6ur9vNL+TdCWK3EBPh9JeydDioHdPoYGg0FO/nMPisdOBvC+xsCufngEUNbVOL/OlengMyDsSlKqRNaa9fUtkv1X55Sylkp1T3ZQ5eBykoph2RLL9uA5knbuwCnnlbYhQ2yywHNxsK4I8bFTtvegu96wN2LZifLFu5FxvLWr38y5Jvj5Mudg3VjWvBhT2cp7NlYqp27UqoK8AlwEsgF1ALGA28BYVrruUqpfBhny9wCqgKzUztbRjp3G6Y1/PGjcdFTQgy0exeavwk5pNBkNK012wOC+WhzIPej4hjXrgpvvFCVPDlzmB1NZJK0du7pXpbJKFLcs4HwW7D9beMD19L1offnUMrF7FQ2IyQ8mg82BrI76DYuZQszr29dnMvIeQy2LsOWZYR4Zval4ZUf4aVvIfwGrGwH+2ZCfIzZyaya1ppfj1+ng6c33udCebdrTTaMayGFXfwPeZ8sMpdSUNsdKrWFXe+BzycQtNno4ss3MTud1bkeFsW76wM4dOEOTSo5MLePC5VlHox4AuncRdbI7wDuK+C1dRAbCas6ww4P42uRqoREzdeHLtN5oQ9/Xr/PzBfr8MvIZlLYxb+Szl1krWqd4I2j8NvHcGw5nN0GPZdAlfZmJ7NY529HMNnLnz+u3ad9DUdmubtQpkg+s2MJCyedu8h6eQpB9wUwdAfkyA0/vAib3oBH98xOZlFi4xNZsvc83Zcc4sqdSBa9Up+vhzSWwi7SRDp3YZ6KLWCMr3FDEN8lcH4PdP8UavU0O5np/P++z+R1/pwJjqBnvTJ81NOZ4gVlHoxIO+nchbly5YWO02DkPihYAta8Dr8OhochZiczRXRcAnO2/8WLS325FxXLl4Nc+ezVBlLYRbpJ5y4sQ5n6MHI/+C4G73lw6QB0mQv1+htn3GQDRy/dxcPLnyt3o3i1SXk8utaicD6ZByOejXTuwnLkyAVt3jaWahxrwMYx8FM/uH/d7GSZKiI6jvc3BNB/5VESNfw8oilz+tSVwi6eixR3YXkcq8PQndB1Plw9Asuawe9fQmKi2cky3L4zt+m80IfVv19jRKtK7JzYmhZVi5sdS9gAWZYRlsnODpqOhupdYOtEY4xBoJdx/9bi1cxO99zCImOZvuU0G/+8SfWSBVn2WgsaVChqdixhQ6RzF5ataEV4fT28uBxC/oLlLeGgJyTEmZ3smWit2XzqJh09vdkWcIsJHaqx9T+tpbCLDCedu7B8SkH9AVClg9HB7/0YTm8wRhiUrmd2ujQLfmAM+vrtr9vUK1eYef2aUrOUzIMRmUM6d2E9CpWEV36Al7+HiGBY2d64OUhctNnJnkprzerfr9HJ05tDF0J5v1st1o9rKYVdZCrp3IX1ce4NTq1h9wdw8NP/DiKr0MzsZP9w9W4kHl4BHLl0l2aVHZjbpy5OxQuYHUtkA9K5C+uU3wFeXGasx8fHwNddYPtkiHlodjLAGPT11cFLuC3yIfDGA2a7u/DziGZS2EWWkc5dWLeqHYxb++2dbtzD9ex26LkIqnY0LdLZYGPQ16nr9+lQswQz3etQurDMgxFZSzp3Yf3yFIRu82HYTsiVD37sCxvGQlRYlsaIjU9k0W/n6PHZQa6HRbHk1QZ8NdhVCrswhXTuwnZUaAajDxo3BDm0EC78ZkyfdO6d6bv+8/p9pqzz5+ztCHrXL8NHPWvjUCB3pu9XiH8jnbuwLbnyQoepMOoAFCoFvw4yhpFFBGfK7h7FJjBrWxB9lvny4FEcqwa7srh/AynswnTSuQvbVLquMYjsyGewfw5cbgJuc4zz5TNoENnhi3fw8ArgWlgUA5pWwKNrTezzyjwYYRmkcxe2K0dOaDUJxvpCCWfYNA5+cId7V5/r14ZHx/Hu+gAGfHkMpWD1yGbMdneRwi4sihR3YfuKV4Mh26HbAvj7OCxrDkdXQGJCun/Vb0G36eTpzZrj1xjVpjI7J7SheZVimRBaiOcjyzIie7CzgyYjobobbJ0EO6fA6fXGIDLHGqn++N2HMUzbEsSWUzepWaoQKwe6Uq98kSwILsSzkc5dZC9FKsBr68D9C7hzDla0Ms6u+ZdBZFprNv15g46e3uwMvMVbnaqz+c1WUtiFxUu1c1dKVQFmAieBcsBdrfX0FNsMAcYAj4d8rNJa/5CxUYXIIEoZd3iq8gLsmAz7ZsLpTcYIgzL1//9mN+8/4oONgew7E0L98kWY368u1UsWMjG4EGmXlmUZB+AXrfUmAKVUkFJqm9b6RIrt+mutr2R0QCEyTcES8NK3UKcfbHsLvnwBWvyHxDZTWP1nKHO2nyEhUTO1hzNDWjiRwy573O5P2IZUi7vW+niKh+yAyCds+qZSKhjID3yutc7aywOFeFa1eoBTS9g9FXwXEXx0LRujhlOvSkvmuNelQrH8ZicUIt3S9YGqUsod2KW1PpPiKW9gm9Y6VCnVDVgLdHjCz48CRgFUqFDh2RILkQnicxdmVZFJHEmowExWsjbPdHSpEagCzmZHE+KZpPkDVaVUe6A9MCnlc1rry1rr0KRv9wFtlVI5nrDdSq21q9ba1dHR8VkzC5Gh/roVTp/lh5mz4wy5qr1Arv8cg2bjUH6rjNMmz+8xO6IQ6Zam4q6U6g64AROAUkqp5kopB6WUfdLzc5RSj98FVAMua63TfxKxEFkoJj4Bz91n6fnZIW7ce8TnAxqwcmAjShYrBl3mwPDdkLsA/NQP1o/O8kFkQjyPtJwt0whYA/gB+4ECwFLAHQgD5gLBwHKl1GXABRiYWYGFyAgnr91jyjp/zoc8pE+Dskzt4UzRlPNgyjeBMQfBZwEc8jQGkXX7BGq7Z9gIAyEyi9Jam7JjV1dX7efnZ8q+RfYVFRvPgl3n+ObwZUrb52VWHxfa1yiR+g8GB8KmN+DWn1Czh3G1q33pzA8sRApKqRNaa9fUtpMrVEW2cej8Hd7d4M/1sEcMbFaRyV1qUCit82BK1YERe+HoUtg/G5Y2BbeZ0GCgdPHCIskVqsLmPXgUx+R1p3h91TFy2tmxZlQzZrxYJ+2F/bEcOaHlBBh72Cj2m/8D3/eCsMuZE1yI5yDFXdi0XaeD6eTpjdfJG4xpW4UdE1rTtPJzDvoqVgUGb4XunnDjD1jeAo4se6ZBZEJkFlmWETYpNCKGaZtPsy3gFrVK27NqcGNcyhXOuB3Y2UHj4f8dRLbrXQj0MkYYlKiVcfsR4hlJ5y5sitaa9Sf/ptNCb/YE3ebtztXZ/GbLjC3syRUuBwN+hT5fQdglWNEavOdDfGzm7E+INJLOXdiMG/cf8f6GAA6cDaVhBWPQV9USWTDoSymo+xJUaW8MIts/C05vhN6fQdlGmb9/IZ5AOndh9RITNT8cuUJnT29+vxzGtJ7OrB3TImsKe3IFikO/r6H/angUBl91hN0fQGxU1uYQAunchZW7GPoQDy9/jl+5R+tqxZnt7kJ5B5MHfdXs9t9BZIc/gzPboOcSqNTa3FwiW5HOXVil+IRElh24QNfFBzkbHMEn/ery/bAm5hf2x/IWhl5LYNBm0InwXQ/YMhGiH5idTGQT0rkLq3P65gOmePkTeCMct9olmdG7DiXs85od68kqt4WxR4x1+KPL4Nwu6LnIOMtGiEwknbuwGtFxCXyy6wy9Pvcl+EEMy19ryBcDXS23sD+WOz+4zYLhe4yO/ueXwWsERN4xO5mwYdK5C6tw4moYk9f5czE0kr4NyzG1Ry2K5M+d+g9aknKuMNrHGELmswAu7oOu86FOXxlhIDKcdO7CokXGxDNt82n6rThCdFwi3w1rwqcv17O+wv5YztzQzsMo8kWdwGs4rH4VHtwwO5mwMVLchcXyORdK54U+fHfkCoOaVWTXpDa0rW4jN3kp6Wws03SeBZcOwLJm4PcNJCaanUzYCCnuwuLcj4rl7bWnGPT17+TJZcevo5vzce86FMxjY6uIdjmgxZsw7jCUrgdbJxqDyO5eNDuZsAFS3IVF2RFwi46ePmz44wbj2lVh+/jWNHZyMDtW5nKoDIO3QM/FcOsULG9pnB8vg8jEc7CxVkhYq5CIaD7adJodgcE4l7bn26GNqVM2k+bBWCKloNEQqNYZtr5lXNkauB56LzWWcIRIJ+ncham01qz1u04nTx/2ngnhHbcabHqzZfYq7MnZl4FXV0PfVXD/KnzRBvbPkUFkIt2kcxemuR4WxXsbAjh4/g6uFYsyt29dqpYoaHYs8ykFLv2gcnvY6QHecyFokzFOuFyqd1cTApDOXZggMVHzre9l3Bb5cPLqPab3rs2vo5tLYU+pQDHo+6UxUjgm3BhEtvM9iI00O5mwAtK5iyx1ISSCKV4BnLh6jzbVHZntXodyRS1kHoylqu4G447Cbx8Z93A9mzSIrHJbs5MJCyadu8gScQmJLN1/gW6LD3Eh5CGfvlSP74Y2lsKeVnntocdCGLINlJ1xyuTm/8Cj+2YnExZKOneR6QJvPGDyOn+CboXTzaUUH/eqg2OhPGbHsk5OrWCMLxyYA0c+h/N7jHu51uxmdjJhYaRzF5kmOi6BeTvP0HupL6EPY1jxekOWvdZICvvzyp0fOs+AEXshnwP88iqsHQoPQ81OJiyIdO4iU/x+OQwPL38u3YnkpUbl+KC7M4Xz5zI7lm0p2xBGHQDfRcZ9Wy8dgK7zwOUlGUQmUi/uSqkqwEzgJFAOuKu1np5im7zAAuAGUA2Yq7U+l/FxhaV7GBPPvB1n+OHoVcoVzccPw5vQupqNzIOxRDlzQ9vJUKunsQa/fiQErDXW5wuXMzudMFFaOncH4Bet9SYApVSQUmqb1vpEsm0mAte01vOVUi7AKkDuKZbN7D8bwvvrA7gVHs3Qlk683bkGBWxtHoylKlELhu2C31fC3umwtBl0mgaNhoGdrL5mR6n+y9NaH0/xkB2Q8kTb7sB7SdsHKKXqKaXstdbhGRNTWLJ7kbHM2BrE+j9uULVEQdaNaUGjikXNjpX92OWAZmOhehfYMgG2/Z8xwqDXZ1CsitnpRBZL1590pZQ7sEtrfSbFUyWAiGTfhyc9lvLnRyml/JRSfqGh8uGPtdNas83/Fp0WerP51E3ebF+VbeNbSWE3m0NLEtS0AAATjElEQVQlGLTJKOrBgbC8BRxaBAnxZicTWSjNxV0p1R5oD0x6wtMhQKFk39snPfY/tNYrtdauWmtXR0dZh7Vmt8OjGf3DCd74+SSlC+dj85uteNutBnly5jA7mgDjA9WGg+CNY1Clg3EB1FcdIDjA7GQii6SpuCulugNuwASglFKquVLKQSlln7TJNqB50rYuwClZkrFNWmvWHL9GR09vvM+F4tG1JhvGtcC5jH3qPyyynn1p6P8TvPQthN+Ale1g30yIjzE7mchkSmv99A2UagR4A35JDxUAlgLOQJjWeq5SKh/G2TK3gKrA7NTOlnF1ddV+fn5P20RYmGt3o3h3gz++F+7SpJIDc/u4UNlR5sFYjagw2Pku+P8CxWsYg8jKNzE7lUgnpdQJrXWqE+RSLe6ZRYq79UhI1Hx7+AoLdp0lh53Co2tNBjSpgJ2dnEttlc7vgS0TjU6+6Rh44QPII3+krUVai7ucpyae6vztCCZ7+fPHtfu0q+HIbHcXyhTJZ3Ys8TyqdYI3jsJvH8Ox5UmDyBZDlRfMTiYykJwAK54oNj6RJXvP033JIa7ciWTRK/X5ZkhjKey2Ik8h6L4Ahu4Au1zwgztsegMe3TM7mcgg0rmLf/D/+z6T1/lzJjiCHnVLM61XbYoXlHkwNqliCxjrC97zwHdJ0iCyT40rXoVVk85d/H+PYhOYs/0vXlzqS1hkLCsHNuLzAQ2lsNu6XPmg4zQYuQ8KloA1r8OvgyDittnJxHOQzl0AcPTSXTy8/LlyN4pXm5THo2stCueTQV/ZSpn6MHI/+C42OvlL3tBlLtTrL4PIrJB07tlcRHQc728IoP/KoyRq+HlEU+b0qSuFPbvKkQvavG3MjHesARvHwI994f41s5OJdJLino3tO3Obzgt9WP37NUa0qsTOia1pUbW42bGEJXCsDkN3Qtf5cO0oLGsOv38JiYlmJxNpJMU9GwqLjGXiL38w7Fs/CubJidfYFnzQw5n8uWWVTiRjZwdNR8O4I1CuMWx/G77tBnfOm51MpIEU92xEa83mUzfp6OnNVv9bTOhQja3jW9Ggggz6Ek9RtCIM3AAvLoeQv2B5SzjoCQlxZicTTyGtWjYR/CCaDzYG8NtfIdQrV5h5I5tSs5TMgxFppBTUH2AMIdv+Nuz9GE5vMEYYlK5ndjrxBNK52zitNat/v0YnT28OXbjD+91qsX5cSyns4tkUKgmv/AAvfw8RwbCyvXGla1y02clECtK527CrdyPx8ArgyKW7NKvswNw+dXEqXsDsWMIWOPcGp9aw+wM45Al/bTG6+ArNzE4mkkjnboMSEjVfHbyE2yIfAm88YLa7Cz+PaCaFXWSs/A7w4jJ4fb0xQvjrLrD9HYiJSP1nRaaTzt3GnA02Bn2dun6fDjVLMNO9DqULyzwYkYmqdjDOqNk3A459AWd3QM9FULWj2cmyNencbURsfCIL95yjx2cHuR4WxeL+9flqsKsUdpE18hSErvNg2E5jnMGPfWHDWGOGvDCFdO424M/r95m87hTnbj+kd/0yfNjDmWIyD0aYoUIzGH0QfD6BQwvhwh7otgBqv2h2smxHOncr9ig2gZlbg+izzJfwR/GsGuzK4v4NpLALc+XKCx2mwqgDUKg0rB1sDCOLCDY7WbYinbuVOnzxDh5eAVwLi2JA0wp4dK2JfV6ZByMsSOm6xiCyI5/B/jlwuQm4zYb6r8kgsiwgnbuVCY+O4931/gz48hhKweqRzZjt7iKFXVimHDmh1SRjZnyJ2sYNQX5wh3tXzU5m86S4W5Hfgm7TydObNcevM6pNZXZOaEPzKsXMjiVE6opXgyHbjPX3v48bg8iOroDEBLOT2SxZlrECdx7G8PGWILacuknNUoVYOdCVeuWLmB1LiPSxs4MmI6F6F9g6EXZOgUAv4+Inxxpmp7M50rlbMK01G/+4QSdPb3YG3uKtTtXZ/GYrKezCuhUpD6+tA/cv4O55WNHKOLtGBpFlKOncLdTN+4/4YGMg+86EUL98Eeb3q0v1koXMjiVExlDKuMNTlRdgx2TYNxNObzS6+DINzE5nE6RztzCJiZofj16l80Ifjly8y9QezniNbSGFXdimgiXgpW/hlZ8g8g582QH2fARxj8xOZvWkc7cgl+9E4uHlz7HLYbSsWow57nWpUCy/2bGEyHy1eoBTK2MQme8iYxBZr8/AqaXZyaxWqp27UqqUUuorpdTxf3m+nVLqT6XUgaT/3sn4mLYtPiGRL7wv0mWRD0G3wpnX14UfhzeVwi6yl3xFjGWZQZsgMd6469PWtyA63OxkViktnXsrYBNQ/ynbTNRaH8iQRNlM0M1wpnj5E3DjAZ2cSzLzxTqUtM9rdiwhzFO5XdIgsplwdDmc2wU9FkL1zmYnsyqpdu5a63VAajM8Byql3lZKTVdKlc+YaLYtJj6BT3efpdfnh7j14BFLBzRk5cBGUtiFAMhdALrMgeF7jKFkP78E60dB5F2zk1mNjFhzDwJmaK2vKKVqA3uUUs5a63/cJl0pNQoYBVChQoUM2LV1OnH1HlO8/LkQ8pA+DcoytYczRQvkNjuWEJanfGMY7QM+C4ybglzYC90+gdruMsIgFc99tozWOkRrfSXp69NAEeCJ3bvWeqXW2lVr7ero6Pi8u7Y6UbHxfLzlNP1WHCYqJp5vhjbG85X6UtiFeJqceeCF92GUt3GO/Lqh8MtrEH7L7GQW7ZmKu1KqgFLKMelrD6WUQ9LXDkBu4HbGRbQNh87fofNCH77xvcLrTSuya1Ib2tcoYXYsIaxHqTow/DfoNAMu7oWlTeHk96C12cksUqrLMkqptsBAoLRS6gPgU2AI4AKMAa4Ai5VSQYAzMFBrLXfLTfIgKo5Z24P41e9vKhUvwJpRzWhaWebBCPFMcuSEluOhZnfYPB42/wcC1kLPJeBQyex0FkVpk/7qubq6aj8/P1P2nVV2BgYzdVMgYZGxjGpTmQkdqpE3Vw6zYwlhGxIT4eS3sPtD49TJDlOh6Riws+1/Y0qpE1pr19S2k4uYMkFoRAzTNp9mW8AtapW25+vBjXEpV9jsWELYFjs7cB0G1dxg6yTY9R4ErjfOlS9Ry+x0ppPxAxlIa43Xib/p6OnNnqDbvONWg81vtpTCLkRmKlwWBqyBPl9B2CVY0RoOzIP4WLOTmUo69wxy4/4j3lsfgPe5UBpWMAZ9VS0h82CEyBJKQd2XoEp72DEFDsyGoE3Q+zMo28jsdKaQzv05JSZqvj9yhc6e3hy/Esa0ns6sHdNCCrsQZihQHPqtgld/gUf34KuOxrya2Cizk2U56dyfw8XQh3h4+XP8yj1aVyvObHcXyjvIPBghTFejK1RsAXs+hMOfwV9bjUFklVqbnSzLSOf+DOISEll24AJdFx/kbHAEn/Sry/fDmkhhF8KS5C0MPRfD4C3G99/1gC0TIPqBubmyiHTu6RR44wFTvPw5fTOcLrVLMf3F2pQoJPNghLBYldrA2MOwfxYcXQbndhuDyGp0MTtZppLOPY2i4xL4ZNcZei/15XZ4DMtfa8iKgY2ksAthDXLnB7dZxhWu+YrA6ldg3XDjBiE2Sjr3NPC7EsZkL38uhUbSt2E5pvaoRZH8Mg9GCKtTrpExo+bQQuO+rZf2Q9f5UKevzQ0ik879KSJj4pm2+TQvfXGEmLhEvhvWhE9frieFXQhrljM3tJtiTJss6gRew2F1f3hww+xkGUqK+7/wPhdK54U+fHfkCoObO7F7UhvaVs9+kyyFsFklnY158W6z4ZI3LGsGft8YYw1sgCzLpHA/KpYZW//C6+TfVHYswNrRzXF1cjA7lhAiM9jlgOZvGKdObpkAWydCoJdxlk2xKmaney7SuSezI+AWHT192PjnDd5oX4Xt41tLYRciO3CoDIM2G9Mlb52C5S3AdwkkxJud7JlJ5w6EhEfz4abT7DwdTO0y9nw3rDG1y8g8GCGyFaWg0WCo1gm2/R/smQqnNxiDyErWNjtdumXrzl1rzVq/63T09Gbf2RAmd6nBxjdaSmEXIjuzLwP9f4Z+X8P9a/BFG9g/G+JjzE6WLtm2c78eFsV7GwI4eP4OjZ2KMrdvXao4FjQ7lhDCEihlnB5ZqR3sehe850HQZqOLL5fqKHWLkO0694REzTe+l3Fb5MPJq/eY0bs2a0Y1l8IuhPinAsWgz0oYsBZiwo1BZDvfg9hIs5OlKlt17hdCIpjiFcCJq/doW92RWe51KFdU5sEIIVJRvTOMOwq/TYOjS+HMVui1BCq3MznYv8sWnXtcQiKf7ztPt8WHuBj6EM+X6/Ht0MZS2IUQaZfXHnp4wpDtYJcTvu9t3MP10X2zkz2RzXfugTce8M46f/66FU53l9JM61Ubx0J5zI4lhLBWTi1hrC8cmGOMEz632yj6Nbubnex/2GznHh2XwNwdxqCvOw9jWPF6I5a+1lAKuxDi+eXKB52mw4i9xg1CfhkAa4fCw1Czk/1/Ntm5/345DA8vfy7dieQV1/K8160WhfPnMjuWEMLWlG0Iow6A7yLwnm8MIusyD+q+bPogMpvq3COi45i6MZCXvzhCbEIiPw5vyrx+daWwCyEyT45c0OYdGHMIilWDDaPgp5fg/nVTY9lMcd9/NgS3hT78eOwqw1pWYvekNrSqVtzsWEKI7MKxBgzbaXTuV32NQWTHvzJtEJnVL8vci4xlxtYg1v9xg6olCrJuTAsaVSxqdiwhRHZklwOajTHu8rRlgjHGIMDLuH9r8apZGiXV4q6UKgXMBOpprRs/4Xk7YDbwEKgIrNJaH83ooClprdkWcIuPNp3mwaM4xr9QlTdeqEqenDkye9dCCPF0RZ1g4Eb48yfY9R6saAnt3oXmb0KOrOmp07KXVsAmoP6/PP8yYK+19lBKOQBHlVK1tNYJGRUypdvh0UzdGMjuoNu4lC3MjyOaUqu0fWbtTggh0k8paPA6VO1odPC/fQSn10PvpVDKJdN3n+qau9Z6HRDxlE26A0eStg0DooFMG6G2/0wIHT298T4Xyrtda7JhXAsp7EIIy1WoFPT/CV7+HsJvwcp2cGRZpu82I94flOB/i3940mP/oJQaBYwCqFChwjPtrFLxAjSsUJRpvWpTqXiBZ/odQgiR5Zx7g1Nr2PU+OFTK9N1lRHEPAQol+94+6bF/0FqvBFYCuLq66mfZmVPxAnw3rMmz/KgQQpgrvwO4L8+SXT3TqZBKqQJKqcc3FN0GNE963AHIC5zOmHhCCCGeRarFXSnVFhgIlFZKfaCUygcMAWYkbfIrEKGU+gj4BBiUmR+mCiGESF2qyzJaa2/AO8XDS5M9nwhMyeBcQgghnoPNXKEqhBDiv6S4CyGEDZLiLoQQNkiKuxBC2CAp7kIIYYOU1s90LdHz71ipUODqM/54ceBOBsYxkxyLZbKVY7GV4wA5lscqaq0dU9vItOL+PJRSflprV7NzZAQ5FstkK8diK8cBcizpJcsyQghhg6S4CyGEDbLW4r7S7AAZSI7FMtnKsdjKcYAcS7pY5Zq7EEKIp7PWzl0IIcRTWPQNsi31/q3plYbjaAcsAu4nPbRNa/1J1iVMO6VUFYxjOQmUA+5qraen2CYvsAC4AVQD5mqtz2V11qdJ43EMAcZg3F0MjP+/fsjKnGmR9O9gC3AMyA1UAYZprR8l28biXxNI87EMwQpeF4CkKbrHgN1a67dTPJep9cuiizsWeP/WZ5TacQBM1FofyJo4z8UB+EVrvQlAKRWklNqmtT6RbJuJwDWt9XyllAuwCmhtQtanSctxAPTXWl/J8nTpd0RrPRNAKbUJ6AP8lOx5a3hNHkvtWMB6XpeZwB//8lym1i+LLu5a63VJXe2/6Q7sTto2TCn1+P6t/lkQL83ScBwAA5VSrhh3svpSa30985Oln9b6eIqH7IDIFI91B95L2j5AKVVPKWWvtQ7PioxpkcbjAHhTKRUM5Ac+T7pPsEVJGrv9uBjmxHgncjbFZhb/mkCajwWs4HVRSg0EfIG6QMEnbJKp9cva19zTfP9WCxcEzNBaLwDWAHuS3rJZNKWUO7BLa30mxVNW9bo85Ti8gXlJr4sfsDbLw6WDUsoN2Aps1Vr7pXja2l6Tpx2Lxb8uSilnoJbWev1TNsvU18TiC0gq0nz/VkumtQ55/BZTa30aKAKUNzVUKpRS7YH2wKQnPG01r8vTjkNrfVlrHZr07T6grVIqR1bmSw+t9S6tdRegklJqXIqnreY1gacfi5W8Lu5AtFLKA2NZtolSamKKbTL1NbG64m4r929NfhxKqcdrbo+PIzdw28x8T6OU6g64AROAUkqp5kopB6WUfdImyV8XF+CUpb39h9SPQyk1J2lpAIwPIS9b4Oc5KKWck47lsctAZSt9TVI9Fmt4XbTWs7TW07XWc4FDwO9a60VZWb8s+jz3pPu3DgK6AMuBT4FhgIvWekzS0sUcIAqogLFWbYlny6R2HP0x1t+CAGeMD/q2mZX3aZRSjTDeFj9+q1wA47aLzkCY1npu0hkCC4BbQFVgtqWdmZHG45gA1MEoMC7AYgv9/6sKxv2LTwK5gFrAeOAtrOg1gTQfi1W8LgBKqb7AGxgN21KMD/KzpH5ZdHEXQgjxbKxuWUYIIUTqpLgLIYQNkuIuhBA2SIq7EELYICnuQghhg6S4CyGEDZLiLoQQNkiKuxBC2KD/B4Wdv208TYDcAAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Examle 1\n",
- "## Simple lines\n",
- "\n",
- "import matplotlib.pyplot as plt\n",
- "import numpy as np\n",
- "\n",
- "#plt.figure(facecolor='y')\n",
- "#plt.figure(figsize=(6,4))\n",
- "\n",
- "A = np.array([1,2,3,4])\n",
- "B = np.array([4,3,2,1])\n",
- "\n",
- "x = np.arange(1,5)\n",
- "\n",
- "# Multiple sets in a single call\n",
- "plt.plot(x,A,x,B)\n",
- "\n",
- "#for i in range(2):\n",
- "# # random array(4) of integer between 0 and 5\n",
- "# C = np.random.randint(0,5,4)\n",
- "# # Multiple times call\n",
- "# plt.plot(x,C)\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Properties of line ( useful for plot and scatter)\n",
- "- String annotation\n",
- " - '-g' *# solid green*\n",
- " - --c' *# dashed cyan* \n",
- "- Parameters\n",
- " - color, linestyle, marker\n",
- " - [ 'blue', 'b', '#0000FF', (0.0, 0.0, 1.0) ]\n",
- " - [ 'solid' '-' , 'dashed' '--' , 'dashdot' '-.' , 'dotted' ':' ]\n",
- " - point '.' , triangle_up '^', square 's' , ...\n",
- " - linewidth\n",
- " - markersize"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 219,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD7CAYAAACRxdTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3Xec1NX1//HXoUkTdSliA8RKR1hE7C0SxRgQ48+GYlBUMIqxoSAiIqASOxIRS4wFwYaCikTFWEBZmiC2KIoxFop0kLL398eZ/S7ZADssM/uZ+cz7+Xj42J2ZDzPn4+yevXM/955jIQRERCReKkQdgIiIpJ6Su4hIDCm5i4jEkJK7iEgMKbmLiMSQkruISAwpuYuIxJCSu4hIDCm5i4jEUKWoXrhOnTqhUaNGUb28iEhWmjFjxuIQQt3SjossuTdq1IiCgoKoXl5EJCuZ2bfJHKdpGRGRGFJyFxGJISV3EZEYUnIXEYkhJXcRkRhKerWMmVUDPgTeCCFcU+KxCsAQYBXQEHgkhDAtlYGKiEjytmcp5GBg1lYeOxOoFULoa2Z5wDQzaxJC2LTDEYqIyHZLalrGzLoB7wMLtnJIJ2AqQAhhKbAOaJaKALfo3/+G5cvT9vQiImmxYQN88UW5vFSpyd3MmgJNQggvbOOwesDKzW6vSNxX8rl6mlmBmRUsWrRou4P9P927Q9Om8MorZX8OEZHyNGsWHHooHHccrF6d9pdLZuTeBVhnZn2BI4FDzaxPiWN+Bnbe7HatxH3/JYQwKoSQH0LIr1u31N2zWzd0KNSuDaedBmefDTvyh0JEJJ3WrYMbboB27eCHH+D++6FGjbS/bKnJPYRwWwhhUAhhGPAe8FEI4R4zq2FmRRl6ItABIDHnXhX4JF1B064dFBTAoEHw/PPQpAk8/TSEkLaXFBEpk86dYdgwOP98+PRTOP30cnlZC0kmRDPrCvQGqgAjgDygRQjh0sRqmaHAGqAB8HBpq2Xy8/NDSmrLfPIJ9OgBH34InTrByJGwzz47/rwiImW1ciVUrgxVq8KUKT7X/pvfpOSpzWxGCCG/1OOSTe6plrLkDrBpk3/U6dcPKlaEe+6BP/4xNc8tIrI9Jk2Cnj3hvPPgtttS/vTJJvd4bGKqWBH69IG5c/2CxdKlUUckIrlm6VJf7PHb30L16j6TEKHISv6mRePGMHkyFBb67eefhwUL4Kqr/A+AiEg6vPkmnHsuLFniMwj9+/uUTITiMXLfnFlxIn/9dRg7VhdaRSS96tWDffeF6dNh8ODIEzvEMblvbtQoH8lXqgSLF/v816+/Rh2ViGS7EODxx+GKK/x2ixbwwQfQunWkYW0u3sndDHbZxb9/4QX/qNSmDUxT2RsRKaMFC6BjR7jwQpg9G9au9fvNoo2rhHgn98317AmvvupLlA4/3Ofhy2GXmIjExKZNcN990Lw5TJ0KDz7oyxyrVYs6si3KneQOcPLJMG8eXHaZL5ds0cIvhIiIlGbxYhgwAI45xvfXXHYZVMjcFJq5kaVLrVowYgS8847PxZ94Ilx0ESxbFnVkIpJpNmzwufXCQth9d5g5EyZOhAYNoo6sVLmX3IscfTTMmQPXX+9vXvPmPmUjIgIwYwbk5/vc+uTJfl/jxhk3t741uZvcwefKhg3z0gXXXAM7J2qfrVkTbVwiEp21a6FvX2jf3osSvviiX0DNMrmd3Iu0bes7XAHeew8aNvSELyK5p3NnuP12H7HPn++3s5CSe0l16sAJJ0CzRK+Rot2uIhJfK1Z4aV6AG2+Ef/wDHn4Ydt012rh2gJJ7SQcfDGPGQM2a/ma3b+8XYJXkReLp1Vf9mtugQX77mGN8gJfllNy3ZcUK2G03uPxyf8M//zzqiEQkVRYvhm7dvMDXzjt7858YUXLflnr1vHznY4/5+vhWrfwC7MaNUUcmIjti8mRv1TlmjK9dnzkTDjss6qhSSsm9NGZexvPTT/0v/A03+FTN7NlRRyYiZbXHHnDggZ7Ub7kFdtop6ohSTsk9WfXrewnh556D77/39a/9+hVfhBGRzBUCjB4NvXv77ebN4d13fZd6TCm5b6+uXX151HnnwZAhxZsbRCQzff2170S/+GL/3c3QQl+ppuReFnl5vqt1xgw49VS/7803YdWqSMMSkc1s2gR33+2j9OnT4aGH/Pc0Qwt9pZqS+45o08b/+i9Z4lfar7026ohEpMjixT6ffsIJPmLv2TOjC32lWrza7EWldm1fVbPffn574UJfJ5+XF21cIrlm/Xp48klfBLH77r7woWHD2E/BbEnu/BlLtyOP9Cvw4NuWmzb1C7AiUj6mT/dSIj16+A5TgEaNcjKxg5J7evzlL7DnnnDGGX4B9ocfoo5IJL7WrPHCf4cdBr/8Ai+/DCedFHVUkVNyT4fWrb3w2NChXvu5aVO/AKtG3SKp9/vf+4Dqoou8icbvfhd1RBlByT1dKlf2sqFz5vjV+gsv9LKh33wTdWQi2W/58uI9JjfdBG+95athinomS+nJ3cwqmNlEMxtgZoPN7Bkzq1bimO5mNs3MpiT+65a+kLPMQQd516cHHvC+i82bw6hRUUclkr0mTPCqrbfc4rePPhqOOy7amDJQsiP3qSGEQSGE/kB14PQtHHNWCOHYxH9/T12IMVChgu+MmzfPL7yqMbfI9lu0CM45x6dd8vLg9C2lISlS6lLIEEIhMBjAzCoBewNbKo94uZn9iCf/B0IIS1MZaCw0bAivvVY89z52LPzrX3Dddd7PVUS27I034NxzfTrmllt8yrNKlaijymhJz7mbWUdgAjAhhFBQ4uF3gNtDCMOBAmDcVp6jp5kVmFnBokWLyhpzdjMr3kjx9tswfnzOLtUSSdpee0GTJjBrlldxVGIvlYXtXMFhZk8A00IID27l8arAKmCnEMKmrT1Pfn5+KCgo+TciB61c6bWkFy3ypiDXX58z26NFtqqw0At9zZoFI0dGHU1GMbMZIYT80o5L5oJqUzPrtNldC4DGZpZnZrUSxwxNTNkAHAAs2FZil80UNeUeP94/brZu7dXqRHLVv/7lJQMuucQb5BQV+pLtksy0zK9ADzPrb2a3AE2A4UBfoFfimB+BkWZ2I3AjoNUy2+uii7zC5Pr1fvW/d28f1Yvkik2bfL16y5ZeZ/3hh3Oq0Feqbfe0TKpoWmYrVq2C/v3hvvtg77197e7JJ0cdlUj6/fST9zA++mh48EGfZ5f/kbJpGSlnNWvCPffA++/796ecAuef75UnReLm1199hF5YWFzo66WXlNhTQMk9U3Xo4BeTbroJnnnGO8Zomkbi5MMPvdBXz57Fhb5ytIJjOii5Z7KddoJBg7wpyI03Fl98VZKXbLZ6Nfz5zz6AWb7c6y+p0FfKKblng5Yt4fLL/ft//tNHN9OmRRuTSFl17uwdki691At9nXJK1BHFkpJ7ttljD/9lKGrsW1gYbTwiyVi2rHhJ44ABXm/pwQehVq1o44oxJfdsc8AB3mmmRg3/ZcnPh3vv9WVkIpno5Zf/u9DXUUf5ihhJKyX3bLZ6tY/k+/TxgmTz50cdkUixn3+Gs87yeut16njzGik3Su7ZrE4dL3/65JPw5ZdwyCFw662+EUokSq+/7rVgXnzRfyYLCvxTppQbJfdsZ+bV8ubP9xKoAwZAu3b+yyQSlX328etCs2b5przKlaOOKOcoucdFvXq+Hn78eFi8GNq391LCa9ZEHZnkgsJCL/B1ySV+u1kzmDLFW0xKJJTc4+a003wU36MH3Hmntx8TSacvvoBjj4VevWDBguL2dxIpJfc42mUXb+U3Zw6ceqrfN2kSrFgRbVwSLxs3wu23+z6MuXPhscf856xq1agjE5Tc461lS/+6ZInPx193XbTxSLwsWeLJ/ZRT/NNi9+4qHZBB1NstF9Su7dMzDRv67W+/9XXydepEG5dkn19/hccfh4sv9kJfc+b4xVPJOBq554r27aF+ff/+wgv9Qtezzxb3cxUpzdSpvtz20kuLr+UosWcsJfdcdO+90KiRbzDp3Bm+/z7qiCSTrVrlG+WOOMI3zr3+Opx4YtRRSSmU3HNRixY+Chs+3Ls/NW3qNbU1ipct6dzZBwS9e8O8edCxY9QRSRKU3HNVxYpw9dXw8cfQpo3X1D7hBPjqq6gjk0zwyy/Fhb4GDvS+vvffX1x2WjKeknuu239/71M5apTXjW/RAkaMiDoqidILL/inuYED/faRR/p/klWU3AUqVPDVD/Pn+1zqxo1RRyRR+PFHL+7VtatffD/rrKgjkh2gpZBSbK+9vHxB0dz7mDHw2WfQr59qg8Tda695jaI1a2DIELjmGr3nWU4jd/lvZj6SB/jgA99xWEE/JrHXsKEvc5w9G264QYk9BvRbK1t3330+H1+xotfm7tdPhcjiorAQHnjAp+PA59jffBMOPjjauCRllNxl26pX968TJvjH9RYt4O23o41Jdsznn3snpD/9Cb77ToW+YkrJXZLzxz96Uq9QAY4/3ku7Ll8edVSyPTZsgKFDoVUrv3j++OM+165CX7FUanI3swpmNtHMBpjZYDN7xsyqlTimqpk9YGY3mNmjZnZg+kKWyBx7rNcSufZaGD3aP8q/8krUUUmyfvnFy0D/7nee3C+4QIW+YizZkfvUEMKgEEJ/oDpweonH+wALQwhDgbuBR1IYo2SS6tXhjjvgww+9INlpp8HZZ8OiRVFHJluybh08+KDPsder55vWxo0rrjMksVVqcg8hFIYQBgOYWSVgb+DzEod1AqYmjp8LtDKzWimOVTJJfr638hs0CJ5/Hpo3V734TPPeez4F07t3caGvvfeONiYpN0nPuZtZR2ACMCGEULJBZz1g5Wa3VyTuK/kcPc2swMwKFmmkl/2qVIGbbvLlcwMHQq3E33PNxUdr5Uq4/HI46ihvlj55sgp95aCkk3sIYVII4bfAvmbWq8TDPwObF52olbiv5HOMCiHkhxDy69atW6aAJQM1bQqXXebfT5kCDRr4GnmJRufOPhVz5ZXeIUmJPSeVukPVzJoC+4YQJibuWgA0NrM8YGMIYQUwEegAvGtmLYA5ifsl1zRo4NvXW7f225s2+Tp5Sa+lS33VS/XqcOutfqG0Q4eoo5IIJTNy/xXoYWb9zewWoAkwHOgLFI3g7wUamll/4GqgRzqClSzQuDE8+qgnmTVrfNfjnXeqXk06PfccNGlSXOjr8MOV2KX0kXsI4Sv+d3UMwHWbHbMW6J3CuCQO1q71ZH/ddTB2LDzySHFfV9lxP/zgF0tffBHatvXaMCIJ2sQk6VO7tieesWNh4UJPQAMGeB9O2TETJ/q1jtde8ybV06b5yhiRBCV3SS8z+MMffNPMOef4fPAhh3gnKCm7xo2hXTvfVHbddVBJBV7lvym5S/moXRv+9jd49VXvyXnEEd6Xc/XqqCPLDps2eau7HonLWU2awBtvwIHaDC5bpuQu5evkk+GTT6BXL09WU6ZEHVHmmz/f16z36eMNNVToS5Kg5C7lb+edvdzs/PnQqZPfN3EiLFsWbVyZZv16GDzYp7G++AKefNKrc6rQlyRByV2i06SJf126FM48E/r2jTaeTLNsGdx9N3Tp4n8Izz1Xhb4kaboKI9HLy4N33/U2fwALFvg6+d13jzauKKxd60tGe/XyQl9z58Kee0YdlWQhjdwlM7RpU5zMe/TwZX5//3txP9dc8M9/+nLGP/2puCGKEruUkZK7ZJ4RI+Cgg+D8831OfuHCqCNKrxUrfKR+zDG+k/cf/4ATTog6KslySu6SeZo08Wma++7z0WyzZsU1yeOoc2f461/hqqt8GkaJXVJAyV0yU8WKPj0xb57XSend20e2n5dsJZClFi8ubjZ+221eRfOuu6BGjWjjkthQcpfM1qgRTJoEjz3mib5VK18fn61CgDFj/NPJzTf7fR06wGGHRRuXxI6Su2Q+M+jeHT79FE49NXtLCH//vU/BnH027LuvX1MQSRMthZTsUb++l7ctWkHz1FO+/vvmm70rVCabMMHXqW/YAMOH+27TbP0jJVlByV2yT9FGnhkz4KOPsqNo1v77e531++/370XSTNMykr3uusuXDVaoAD/95NURV62KOiq3aZPvLu3e3W8ffLCX51Vil3Ki5C7ZrajOyuuv+3RH8+ZeLTFKn3ziVS///GdfFaNCXxIBJXeJhwsu8LXxVatCx45w4YVes6Y8rV8PgwZ5oa+vvoKnn4ZXXlGhL4mEkrvExxFHwOzZ0K+fly5o2hSef778Xn/ZMt94VdSc5OyzVehLIqPkLvFStaqXyS0o8LosZ5wBXbt6v9F0WLPG191v2lRc6Oupp6Bu3fS8nkiSlNwlnlq39pU0w4Z5rfiWLb2GSyq9/Ta0aOHLGouajuyxR2pfQ6SMlNwlvipVguuv9z6jQ4ZArVp+/y+/7NjzLl8Ol1wCxx/v0y5vv616MJJxlNwl/g46CC6+2L9/6y1o0ADef7/sz9e5M4weDddeCx9/DMcem5IwRVIpC3Z/iKTQ/vvDOed4/XjwHaOVK5f+7xYt8qJe1avD0KG+u7Rdu/TGKrIDNHKX3NKgATz0EFSr5hdDW7f2KZsNG7Z8fAi+pHHzQl+HHabELhmv1ORuZvuZ2TNmdq2Z3WtmA7ZwTHczm2ZmUxL/dUtPuCIptG6db3rq18+T9cyZ//34v/8Np53mNWH23794t6lIFkhm5J4HjAkh3BlCuBI4y8zabuG4s0IIxyb++3tqwxRJg7w8ePZZePFFL19w6KHepHvtWnj5ZV8n/9ZbXkbg/fe9aYhIlig1uYcQpocQxpf4N6u3cOjlZnaNmQ0ws7yURSiSbp07+6aj7t3h9tt9qmbFCjjySF+3rgqOkoW2a87dzLoAk0IIn5V46B3g9hDCcKAAGLeVf9/TzArMrGDRokVlClgkLXbe2Yt7nXiiz7936+Y11+vUiToykTJJOrmb2XHAccBVJR8LISwIIRRl67eAY8zsf4Y6IYRRIYT8EEJ+Xe3gk0zx8cfeDenaa31FzPTpPlofOdLr1YhkoaSSu5l1AjoCVwL1zayDmeWZWa3E40PNrGhZ5QHAghDCprRELJIqv/7qK2DatoWFC2HsWJ9/r13b59k/+ww6dfJjX34ZliyJNl6R7VDqOvfExdNn8emWt4EawAigC7AUGAb8CIw0swVAC0CrZSTzrVgBDz7oBb7uvtuT+uYOPNC/Ll3qa+PPPdeXUYpkgVKTewhhBlCzlGOyuGOx5JTVq2HUKLjiCi/uNW8e7L77tv9NXh588IG3+QMv51utmhcmE8lQ2sQkuePNN73Q15//DO+84/eVltiLtGzpVR/BSxk0bQqPPlrcz1Ukwyi5S/wtWwYXXeQrYSpV8sR+/PFlf76HHoJWraBHD/jNb+Drr1MXq0iKKLlL/HXpAo8/Xlwh8uijd+z5DjjAK0GOHOllhVu0gHvu8ZruIhlCyV3i6aeffH4dvKb7hx/612rVUvP8FSrApZd6v9TjjoOrrvJNT/Pnp+b5RXaQkrvESwjFLfaKCn21b+/LHdNhn328T+pTT8GXX/ru1r/8JT2vJbIdlNwlPhYu9HXp55/vNdx79Cif1zXzpZKffuot/VL16UBkB6ieu8TD+PFw3nk+cr/vPujVq/zrwdStC888U7yC5oknvDbNbbdBlSrlG4vkPCV3yW4h+Mj54IO9I9L990OjRtHGZOZf583zuf5K+jWT8qdpGclOGzd6Bcduic3QBx3kc99RJ/bN3XEHTJ7sF19//NEvuqa6SbfIVii5S/aZM8cvkvbt692U1q2LOqKt22kn//qPf/h0UbNmMHFitDFJTlByl+yxbh307w/5+fD99/Dcc/DCC1C1atSRle6882DqVNh1Vzj1VK9To7LXkkZK7pI9Vq703aHnnuvrybt2jTqi7XPooTBjBgwcCOPG+XLNMWNUwkDSQsldMtuqVTB8uO/+rFvXk/rjj3sxr2xUpYqvv585Exo39oqUv/+992sVSSEld8lcb7zhDayvuw7++U+/Ly5NXpo390qTd93l8/GtWsHy5VFHJTGi5C6ZZ+lSuPBC6NjR59Pffde3+MdNxYq+gmbuXP90sssufv/ixdHGJbGg5C6Zp0sXLyFw440wezYccUTUEaXXfvv5HzPwUXzDhmrvJztMuyskM/z4ozeprlED7rzT56Zbt446qvLXpAl07+4rggDWr9fuVikTjdwlWiH4BdKmTWHAAL/v0ENzM7ED7LUXjBjh9WlWr/YmIQMHepIX2Q5K7hKdb76B3/7WpySaNYOePaOOKLOsX+8j+FtugTZtvJSBSJKU3CUaL75YvGLkgQe8O9JBB0UdVWbZbTd48kmYMMFX0nTo4C0Ci+rUi2yDkruUr6INO82aedu7efOgd2+vvyJb1qmTNwW55BK4+26fqnnrraijkgyn3ygpHxs2wJAhvrsU4MAD4aWXfGWIlK5WLW/rN2WK/yE84QRv1L1sWdSRSYZScpf0mznTL5L26+c7TX/9NeqIstcxx8DHH/vGrsce83o1Ilug5C7ps3Yt3HCDJ/Yff/R59mefLa6UKGVTrZqXO/7iCzj5ZL/vhRfg55+jjUsyipK7pM/q1fDII3DBBV4TpnPnqCOKl8aN/esvv/j/45tuijYeySilbmIys/2AwcBMYG9gSQhhUIljqgLDge+BA4BhIYQvUh+uZLyVK31u+OqroU4dT+p16kQdVbzttpsvk6xXz29/+aWXbdhnn2jjkkglM3LPA8aEEO4MIVwJnGVmJVvJ9wEWhhCGAncDj6Q4TskGr73mq2D69i3ePq/EXj6aNi3+f33JJf4+jBwJhYXRxiWRKTW5hxCmhxDGl/g3JRfadgKmJo6fC7Qys1opi1Iy25IlcP75cMopULMmvP++9zOVaIwe7dc5evXygmtffhl1RBKB7ZpzN7MuwKQQwmclHqoHrNzs9orEfSX/fU8zKzCzgkXqQhMfp58Ozzzjc76zZvlmG4lO48beu3X0aG9J2LKl93PduDHqyKQcWUiyC4yZHQd0AfqEEApLPPYucGMI4d3E7RXA3iGErXYDzs/PDwUFBWUOXCL2ww9e6KtmTSgogMqVvSa5ZJb//Mc3ib30ErRt6xe49T5lNTObEULIL+24pEbuZtYJ6AhcCdQ3sw5mlrfZ1MtEoEPi2BbAnG0ldsliIcCjj3r1wqJCX/n5ShiZas89fZnk2LHw3Xf+Xg0bFnVUUg5KTe6Ji6fPAocBbwPjgYOAvkCvxGH3Ag3NrD9wNdAjLdFKtL7+Gk46CXr08GR+6aVRRyTJMIM//MFXLp1zjq+ukdgrdSlkCGEGULOUY9YCvVMVlGSgF16Abt28e9DIkV7BUfVgskvt2vC3vxXX93n8cb9Gcscd2lgWQ2rWIdsWgo/8WrTw8rz33KP109nOzL9+8YWXMqhcOdp4JC009JItW78eBg/2j/EhwAEHwPPPK7HHyZAh3oS8QgW/QH755b7bVWJByV3+V0EBtGtXvJ1dXYDiq2jU/vbb8Ne/+maoF1+MNiZJCSV3KbZ2rVcbbN8eFi+G8eN9/brmY+PvnHPgo4+gfn3ft3DmmfDTT1FHJTtAyV2KrV7tF9l69PDmEKedFnVEUp7atPEEP2QIvPyyL3d94oniC7CSVZTcc92KFb7uedMmr03y6acwahTsumvUkUkUKlf2Ms2zZ3tyv+ACLyv87bdRRybbSck9l02c6AWm+vUrLvRVu3a0MUlmOPhg/5m4/3547z1o3dr7uErWUHLPRYsWebu7U0+FXXbxJtUq9CUlVajgK2g++QTuu89/VkBz8VlCyT0Xde0K48bBwIHeAq99+6gjkkzWsKFvYANfOtmoEbzzTqQhSem0iSlXfP+9j7xq1oS77/YVMM2bRx2VZJuWLb1efNGAYN06bwwiGUcj97gLAR5+2NcvFxX6attWiV3Kpn5936VctSqsWuU7l/v18yQvGUXJPc6++gpOOMHrwLRt66VfRVJl0yY48khfOtm6tTdpkYyh5B5Xzz3no6oZM3xp45tvwn77RR2VxMkuu8Bjj8GkST5yP+oo+NOfvI+uRE7JPW6KNpy0agWdOvlKh4svLi4WJZJqJ50E8+Z5Yh8xwqf8Jk2KOqqcp+QeF+vXwy23wFlnFRf6GjcO9t476sgkF9SsCffe62vjq1f3CqIXXABLl0YdWc5Sco+Djz7yOfWBA6FSJRX6kugccYTXiO/XD55+2n82JRJK7tlszRq45hpvSP3LL/DKK/DUUyr0JdGqWtXLRX/1lY/gwdv8/fBDtHHlGCX3bLZ2LTz5pK+GmT/fd5yKZIoGDfzrsmVw0UX+yVLKjTYxZZvly+GBB+D6670OzKefqiemZLZdd/UeAUV1iz7/3D9dNmoUaVhxp5F7NnnlleLNSO+95/cpsUs2OPDA4uR+2WW+oua++3ytvKSFkns2WLQIzj7b66vXrg0ffqhCX5K9Hn/c18RfeSUcfbR/+pSUU3LPBl27ev/SQYP8421+ftQRiZRdgwbw6qveCOSzz3x36223wYYNUUcWK0rumerf//baHeC1PGbN8p6mVapEG5dIKph5pcn586FzZ+jf3wctM2ZEHVlsKLlnmsJCeOghn1svalDdpo031RCJm913h2ef9abcP//s1SYHD446qlhQcs8kX34Jxx8Pl14Khx7q27lFckHnzj6K797dE77ssFKTu5nVN7PRZjZ9K48fa2azzWxK4r9rUx9mDhg3zmtlz54NjzwCkydD48ZRRyVSfnbbDUaP9lpI4N/36qVywmWUzDr3I4HxQOttHNMnhDAlJRHlmhB8/vGQQ+D3v4e77oI994w6KpHoLVwIX3yh60xlVOrIPYTwHFBaDc9uZnaNmQ0ys31SE1rM/fqrr1c/80xP8PvvD2PGKLGLFBk0CF5/3Xu5/uc/3gFqyZKoo8oaqZhznw/cGkIYDjwLTDazLT6vmfU0swIzK1i0aFEKXjpLTZvmF0lvvRWqVVOhL5GtqZSYXHj3XXj0UWjSxOvUFJW2lq3a4eQeQvg5hPBN4vtPgF2BLY7eQwijQgj5IYT8unXr7uhLZ5/Vq+Gqq+Dww72hQdFaXxX6Etm2//f/fJlkw4b+fZcuPpprQKkFAAAKJElEQVSXrSpTcjezGmZWN/F9XzPLS3yfB1QBfkpdiDGybp1PvfTq5U00Tj456ohEskfLljB1Ktx5pzcDadrUFx9oFL9FyayWOQboBuxhZv3NrBrQHbg1ccg3wL1mdgNwL9AthKDL20WWLfPpl40biwt9PfAA7Lxz1JGJZJ9KlbzM9dy5vrP1oovgxBPh66+jjizjWIjor15+fn4oKCiI5LXLzUsv+Sj955/hrbe8joaIpEZhITz8MFx7rV90/eYbr0AZc2Y2I4RQag0SbWJKh59+8lUwXbpAvXpe6EuJXSS1KlTwFTTz58ODDxYn9u+/jzauDKHkng5nnAHjx/s26unTvQWeiKTH3nvDOef495Mm+ea/t9+ONqYMoGYdqbJwoe+w23lnr1O9005+wUdEyk+bNl5K+PDD/fbatb7cOAdp5L6jCgthxAgv7DVggN93yCFK7CJRqFsX7rjDB1crV/rv5XXXeb/hHKPkviM+/xyOOQYuv9ybVF95ZdQRiUiREOA3v/Glk61awTvvRB1RuVJyL6uxY/0HZt48eOwxn+tTT0iRzFGrlpfPfustT/THHust/lasiDqycqHkvr2Klo62bQunn+7r1rt39+JfIpJ5jjsOPv4Yrr4aRo3yqZqJE6OOKu2U3JO1bh306+crYUKA/faDp5+G+vWjjkxESlO9Ogwf7jtcd90VTj0VzjsPFi+OOrK0UXJPxgcf+EXSIUN8NYwKfYlkp0MP9Ro1Awf61OrMmVFHlDZK7tuyahVccQUceaRfbX/9de/crkJfItmrShW4+WZYsABOOsnve/pp71scI0ru27J+PTz3HPTu7RdOO3aMOiIRSZW99vKvy5b5hdZbb9328VlGm5hKWrrUNyH17w95eX7BdJddoo5KRNJl111h1qzi8gWffgqVK3sDnSymkfvmnn/eNx8NHuzz7KDELpILGjf2wRz4vpWWLeEvf4FNm6KNawcouQP88AN07eorYfbcEwoKVOhLJFc98YRvfrrmGt+cOG9e1BGViZI7eAXHiRNh2DD46COvEy0iuWmvvbxc95gxXka4TRtfXZNlq+RyN7l/+63XngC4/36YMweuv764Z6OI5C4zb+c3f75/veUWT/IffRR1ZEnLveReWOjJvFkzuOkmv691azjooGjjEpHMU6cO/P3vMGECLF/u0zQDB0YdVVJyK7l/9pnPpV9xBRx1lDerFhEpTadO3vf4kktgn32ijiYpuTMHMWYMXHAB1KzpF0zOO0/1YEQkebVqecenIqNGeTOe+++HqlWji2sr4j9yLyz0r+3awR/+4HNo3bopsYvIjvnpJ/juu4zdsR7f5L52LfTt60sciwp9Pfkk7L571JGJSBzcdJOvsjPz0gUXXgg//xx1VP8nnsn93Xf9Iuntt0Pt2rBhQ9QRiUgcVazoX6dN8/o0TZr4ILKoNHiE4pXcV670OjBHH+0JffJkGD3aCwWJiKTLGWfA7Nm+6q5bNy8p/N13kYYUr+S+YYNvPujTB+bOhRNPjDoiEckVTZr4rMG998KUKb7ceuTI4ut+5Sz7k/uSJd6YeuNGrw3x2Wdw991Qo0bUkYlIrqlY0Zdaz5sH7dtDr17eCerLL8s9lFKTu5nVN7PRZjZ9K49XMLNhZtbfzB42s8NSH+YWhADjxnmhr6FDvcMKeDMNEZEo7bsvvPEGPPqot/jLz/fSwuUomZH7kcB4YGtrB88EaoUQBgPXA0+YWcUUxbdl//mP9y8980zfUFBQ4JuSREQyhZmvoJk/Hx5+uLik8MKF5fLypSb3EMJzwMptHNIJmJo4dimwDmiWkui25swzvSvSHXf4VepWrdL6ciIiZbbHHp6zAF57zWvUrF6d9pdNxQ7Vevx38l+RuO9/mFlPoCdAgwYNyv6KI0ZAtWpw4IFlfw4RkfLWvr33bi2Ha4KpuKD6M7D5RHetxH3/I4QwKoSQH0LIr1u3btlfsVUrJXYRyT55eXD88eXyUmVK7mZWw8yKsvNEoEPi/jygKvBJasITEZGySGa1zDFAN2CPxIqYakB3oKib7FhgpZndDNwJnB9CyN7eVCIiMVDqnHsI4R3gnRJ3j9js8UJ8lYyIiGSI7N/EJCIi/0PJXUQkhpTcRURiSMldRCSGlNxFRGLIQkRF5c1sEfBtGf95HWBxCsOJks4lM8XlXOJyHqBzKdIwhFDqLtDIkvuOMLOCEEJ+1HGkgs4lM8XlXOJyHqBz2V6alhERiSEldxGRGMrW5D4q6gBSSOeSmeJyLnE5D9C5bJesnHMXEZFty9aRu4iIbEMqmnWkjZnVBwYDrUII7bbweAVgCLAKaAg8EkKYVr5Rli6J8zgWuAcoarI4MYRwZ/lFmDwz2w8/l5nA3sCSEMKgEsdUBYYD3wMHAMNCCF+Ud6zbkuR5dAcuxbuLgf98/b0840xG4vfgFeBDoAqwH/DHEMLazY7J+PcEkj6X7mTB+wKQqKL7IfBGCOGaEo+lNX9ldHKnuH9r6608XtS/tW+ilvw0M2uSgSWHSzsPgD4hhCnlE84OyQPGhBDGA5jZfDObGEKYsdkxfYCFIYQ7zKwF8AiQaU1ukzkPgLNCCN+Ue3Tbb2qijzFmNh44HXhqs8ez4T0pUtq5QPa8L4OBWVt5LK35K6OTewjhucSodms6AW8kjl1qZkX9Wz8uh/CSlsR5AHQzs3y8k9XDIYTv0h/Z9gshTC9xVwWgZEPITsCNiePnmlkrM6sVQlhRHjEmI8nzALjczH4EqgMPJPoEZ5RE2e2iZFgJ/yTyeYnDMv49gaTPBbLgfTGzbsD7QEug5hYOSWv+yvY596T7t2a4+cCtIYThwLPA5MRHtoxmZl2ASSGEz0o8lFXvyzbO4x3g9sT7UgCMK/fgtoOZdQQmABNCCAUlHs6292Rb55Lx74uZNQWahBBe2MZhaX1PMj6BlCLp/q2ZLITwc9FHzBDCJ8CuwD6RBlUKMzsOOA64agsPZ837sq3zCCEsCCEsStx8CzjGzCqWZ3zbI4QwKYTwW2BfM+tV4uGseU9g2+eSJe9LF2CdmfXFp2UPNbM+JY5J63uSdck9Lv1bNz8PMyuacys6jyrAT1HGty1m1gnoCFwJ1DezDmaWZ2a1Eods/r60AOZk2sd/KP08zGxoYmoA/CLkggy8noOZNU2cS5EFQOMsfU9KPZdseF9CCLeFEAaFEIYB7wEfhRDuKc/8ldHr3BP9W88HfguMBP4C/BFoEUK4NDF1MRRYAzTA56ozcbVMaedxFj7/Nh9oil/omxhVvNtiZm3xj8VFH5Vr4G0XmwJLQwjDEisEhgM/APsDQzJtZUaS53El0BxPMC2AezP052s/vH/xTKAy0AS4AvgzWfSeQNLnkhXvC4CZdQV64wO2EfiF/HLJXxmd3EVEpGyyblpGRERKp+QuIhJDSu4iIjGk5C4iEkNK7iIiMaTkLiISQ0ruIiIxpOQuIhJD/x/rE1sGWiGx0wAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Examle 2\n",
- "## Simple lines - Change properties of lines\n",
- "import matplotlib.pyplot as plt\n",
- "import numpy as np\n",
- "A = np.array([1,2,3,4])\n",
- "B = np.array([4,3,2,1])\n",
- "x = np.arange(1,5)\n",
- "# Multiple sets in a single call\n",
- "plt.plot(x,A,'r--',x,B,'r-.')\n",
- "lines = []\n",
- "#for i in range(2):\n",
- "# # random array(4) of integer between 0 and 5\n",
- "# C = np.random.randint(0,5,4)\n",
- "# # Multiple times call\n",
- "# handle, = plt.plot(x,C)\n",
- "# lines.append(handle)\n",
- "## Modify properties at convenience\n",
- "## Line2D objects\n",
- "#lines[0].set_color('green')\n",
- "#lines[0].set_linestyle(':')\n",
- "#lines[0].set_marker('^')\n",
- "#lines[1].set_color('cyan')\n",
- "#lines[1].set_linestyle('-')\n",
- "#lines[1].set_marker('o')\n",
- "\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 220,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD7CAYAAABpJS8eAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAFphJREFUeJzt3X/QZXV92PH3B1EX427LxmcT2wxggCQ6IM3wmMkGUXfQamZjKoR2als7HRmXIU4QlRays3GI3dAF10aZpiU7ITNNMrWZrAWj24bClkZCV/DZpMpUaaBas6aV50mkebbVJbB8+sc9z+7dh+f3/Z57zj3n/ZrZ2XvOvc/9fs+9dz7nc76/TmQmkqTuO6vpCkiSxsOAL0k9YcCXpJ4w4EtSTxjwJaknDPiS1BMGfEnqCQO+JPWEAV+SeuLspisw7FWvelVecMEFTVdDkibK0aNH/ywzp1Z7XasC/gUXXMDMzEzT1ZCkiRIR31jL62zSkaSeMOBLUk8UadKJiAuAw8CxatcW4MvAh4B9wNeAi4Hdmfl0iTIlSetTKsM/DlyfmW/JzLcAnwV+DbgdeDAz9wH3AfsLlSdJWqciAT8z/zwzHwSIiJcD05n5B8BO4Ej1skeqbUlSA+pow/97wKeqx9sYZP8A88C5EXFGM1JE7IqImYiYmZubq6E6krpqdv4Eb7rzIWaPn2i6KhOhjoD/t4Hfrh7PApurx1uAZzLz+eEXZ+aBzJzOzOmpqVWHkUrSKXcdfpJjz3yHuw4/1XRVJkLRgB8RO4D/kpnPVbsOAdurx1dU25I0stn5E/zO0W+SCQdnjpnlr0HpDH8XcPfQ9m7gbRGxB7gGuLlweZJ66q7DT/JCdU/uk5lm+WtQdKZtZr570fa3gfeVLEOSFrL7504OAv5zJ5ODM8e48aqL2LZ5U8O1ay8nXkmaOMPZ/QKz/NUZ8CVNnAe++vSp7H7BcyeTB77yrYZqNBlatXiaJK3Fo7vf2nQVJpIZviT1hAFfknrCgC9JPWHAl6SeMOBLUk8Y8CWpJwz4ktQTBnxJ6gkDviT1hAFfknrCgC9JPWHAl6SeMOBLUk8UWS0zIn4YeDfwXeDNwG0M7mf7C8BTwAXAhzPz/5YoT5K0fiMH/Ih4CfDPgXdm5gsR8RvA88BvAh/JzMci4ueAWxicACRJDSjRpPMGIICfi4ifB94J/B9gB/DF6jWPADsLlCVJ2qASTTrnA9uBd2fmX0TEbwHfC3w389Q9yOaBbUv9cUTsYnDzc84777wC1ZEkLaVEhj8PPJGZf1Ft/wFwCXBORES1bwuDNv0XycwDmTmdmdNTU1MFqiNJWkqJgP8o8L1VWz4MMv7/BjzEoLkH4ArgUIGyJEkbNHKTTmZ+OyJuAT4REXPAFPBR4N8AH4mIvwmcB3xo1LIkSRtXZFhmZt4L3Lto9/8E3lvi/SVJo3PilST1hAFf6oDZ+RO86c6HmD1+oumqqMUM+FIH3HX4SY498x3uOvxU01VRixnwpQk3O3+C3zn6TTLh4Mwxs3wty4AvTbi7Dj/JC9Ucx5OZZvlalgFfmmAL2f1zJwcB/7mTaZavZRnwpQk2nN0vMMvXcgz4UiFNjJR54KtPn8ruFzx3MnngK98aWx00OYpMvJJ05kiZve+6ZCxlPrr7rWMpRy82O3+Ca+8+wsEbtrNt86Y1P9ckM3ypAEfK9M9KQ2HbOkzWgC8V4EiZflnpBN/mk78BXxqRI2X6Z6UTfJtP/gZ8aUSOlOmXlU7wbT/5G/ClETlSpl9WOsG3/eTvKB1pRI6U6ZfVTvDLPTeukVsrMeBL0jpM8gneJh1J6oliAT8ivhAR/7n6d7jatzUiDkTErRFxT0R8X6nyJGnSNH3fgpIZ/u9l5luqf1dV+24HHszMfcB9wP6C5UnSRGl6QlbJgH9pRNwSEbdFxM5q307gSPX4kWpbknqnDROySnba3pGZj0XES4DPR8RxYBtwvHp+Hjg3Is7OzOcX/igidgG7AM4777yC1ZGk9lhqQta4R+4Uy/Az87Hq/5PAw8AOYBbYXL1kC/DMcLCvXn8gM6czc3pqaqpUdSSpNdoyIatIwI+IH4mI64Z2XQw8BRwCtlf7rqi2JalX2jIhq1SGPw/8VET8QkR8DDgGfArYDbwtIvYA1wA3FypPkibGapO1xjV6p0gbfmb+L+DqJZ76NvC+EmVI0qRabbLWuO6l4MQrSWrQOEfvGPAlqUHjXE7ZgC9JDRn36B0DviQ1ZNyjdwz4ktSQcd9LweWRJWkFs/MnuPbuIxy8YTvbNm8q+t7jXmrZDF+SVtD0gmclGfAlaRltWPCsJAO+pDVpei33JoxzyOQ4GPAlrUmXmjbWoi0LnpVkwJe0qqabNpq4umjLgmclGfAlrarppo0mri7GPWRyHByWKWlFyzVt3HjVRWzbvKnWYYvD5S9cXSyUW7dxD5kcBzN8SStarWmj7uy76auLLjHgSzWb9NEtKzVt1N2238WO0ybZpCPVbFxrnddlpaaNPfc+Xut9Wle6upjEz7JpxTL8iDgnIr4cEfur7U0R8S8i4ucj4tcj4odKlSVNiqZHt9RpHNl3FztOm1Qyw98L/NHQ9k3An2TmnRFxKXAPcGXB8qTWW6r9uSuZ6Tiy7y52nDap1E3M3wM8Anx9aPdO4AhAZj4OXBYRW0qUJ02Crrc/m31PnpEz/Ih4HfDazNwdEa8femobcHxoe77aNz9qmdIk6Hr7s9n35CmR4V8NnIiIW4E3Aj8WETcBs8DmoddtqfadISJ2RcRMRMzMzc0VqI7UDmbAapuRM/zM/KWFxxGxCXhlZn6ierwdeLhqw/9SZr4ou8/MA8ABgOnp6Vz8vDSpzIDVNsU6bSPiZ4A3AS+LiHcDnwT2R8Qe4CLgulJlSZLWr1jAz8xPA59etPv9pd5fkjQaZ9pKUk8Y8CWpJwz4ktQTBnxJYvIXuVsLA76kXlkusPfhFo4GfEm1aGvGvFRg7/Iid8MM+JJq0caMebnA3pebrBjwJZ2hRGbe1ox5qcDe9UXuhhnwJZ2hRGbexox5ucB+x+89seItHLvEgC/plBKZeVsz5uVWL/33j3+rN4vceYtDSaeUuGHLKMtCz86f4Nq7j3Dwhu1s27xpfZVf5b2WW7106/eczVf/6TtGKmtSGPAlActn5jdeddG6gu9Ky0KvFvBL3v938Xu5eqkBX+q09WTMpW7YstHAurg5ab0nmrreq0tsw5c6bD0dsE3fsKVkR28bO43bwAxf6qj1ZrlNNnmUak4q/V5dY4avTmnr7M4mrJbltumzWqk5qcn36hoDvjqljbM7m7CWoZFt+qxKNic13TTVZiM36UTEWcBngUeBlwEXAu8FzgH2AV8DLgZ2Z+bTo5YnLceOutNW64Bt22dVsjnJ0TjLK5XhH8nMj2bmHuAVwDXA7cCDmbkPuA/YX6gsaUl21J22WpbrZ9VPkYuygJHeLOJsBpn+9cC9wE9k5rGI2Ao8lZlbV/r76enpnJmZKVYf9cfs/AmuvPMhnn3+hVP7Np19Fp+/ZUdvs/zl+Fl1T0Qczczp1V5XrA0/It4OfA74XGbOANuA49XT88C51Qlh8d/tioiZiJiZm5srVR31jB11a+dn1V/FAn5m3p+Z7wBeExE/C8wCm6untwDPZObzS/zdgcyczszpqampUtVRz9hRt3Z+Vv1VotP2dcBrMvNQtevrwA8Ch4DtwDHgimpbKmLxDFI76tbOz6q/Sky8eha4LiJ+FHgp8FrgRuAvgTsi4ocYjNy5uUBZElB2zRWpL0YO+Jn5PxiMylnK+0Z9f3XfeldIbNuQQmlSOPFKjVvvBCCHFEobY8BXo9Z7w406bq7RpiUGpDoZ8CfcOIJVnWWsN1uvY0hhm5YYkOpkwJ9w4whWdZWxkWy99JDCtt5sW6qDyyNPsHF0XtZZxkZuuFF6SGGJW/pJk8IMf4KNo/OyzjKangDU1pttS3Uxw59Q47jJQ91lND0BqNQt/aRJYYY/ocaxHkrX11xp+gpDGjcz/Am1UrAqlZ2Oo4wmNX2FIY1b0eWRR+XyyJK0fmNfHlmS1G4GfI2NM1rXzs9KdTDga2yc0bp2flaqgwFfY+GM1rXzs1JdDPgaiy6tcFl3c0uXPiu1iwFftevajNY6m1u69lmpXUYO+BFxYUR8KiL+cUR8MiI+Uu3fGhEHIuLWiLgnIr5v9OpqEizOgLs0gavu5pYufVZqnxIZ/lbg32bmxzLzA8DfjYjLgduBBzNzH3AfsL9AWZoAizPgLs1orbu5pUufldqn+MSriHgCeBfwAPATmXksIrYCT2Xm1pX+1olXk292/gRX3vkQzz7/ApvOPovP37KjM7cfHD62BV07Rk2mRiZeRcTVwP2Z+QSwDThePTUPnBsRLuXQcaUz4DaNR7e5RZOuWMCPiB3ADuCD1a5ZYHP1eAvwTGY+v8Tf7YqImYiYmZubK1UdNaCODscmx6MvPtnY3KJJVyTjjoidwJXAB4BXR8T5wCFgO3AMuKLafpHMPAAcgEGTTon6qBmllxsexw1eVjJ8stn7rktcbE0Tr8QoncuB3wZ+HHgI+Azww8Bu4G0RsQe4Brh51LLUbqUz4CbHozv5SV00coafmUeBVy7z9PtGfX9NjpIZ8Dhu8LISb32oLnLilVqpdAfpejp/nfxUvzZ1xveJAV+tVEfz0Fo7fx2NUz8Xh2uGwyTVSnU0D62187frd/pqWtOd8X1mwFfnrbc93tE49bJ/pDk26XSUbaQDtse3i99Hswz4HWUb6YDt8e3i99EsA34HOYb8NGfHtovfR7Nsw+8g20hPsz2+Xfw+mmWG3zHjbCO1n0CaLAb8jhlnG6n9BNJkMeA3oM7MeFxtpPYTSJPHNvwGLF6FsaRxtZHaTyBNHjP8MetCZuxY6nLsB9E4GfDHrMklf0txLHU59oNonAz4Y9SVzNix1GV04WpPk8U2/DEqfUeopjiWugz7QTRuZvhjZGasBV252tNkKXVP2+8H9gKXZeYbqn2bgP3AnwIXA/sy849LlDepzIy1oCtXe5ospTL8NzK4l20M7bsJ+JPM/GfALwP3FCpLmnhe7akJRTL8zDwYEW9ZtHsngxuZk5mPR8RlEbElM+dLlNk3s/MnuPbuIxy8Ybs3i+gAr/bUhDrb8LcBx4e256t9Z4iIXRExExEzc3NzNVanPuMYS+3wPYHj9jWaOgP+LLB5aHtLte8MmXkgM6czc3pqaqrG6tSn7mDs8D0t8MSvUdQZ8A8B2wEi4lLgS11szhlHMO7CZC2NzhO/RlUk4EfEm4H3AK+OiD0RcQ7wSeD8iNgDfBi4rkRZbVN3MHb4nhZ44teoigT8zPz9zLwuM/96Zu7NzO9W/95fbf+jLg7JHEcwdhkDgSd+leHEqxGMIxg7fE/giV9luLTCCFYKxqUmzzh8TzCe35q6L3JR1tCk6enpnJmZaboakjRRIuJoZk6v9jqbdCSpJwz4ktQTBnxJ6onOB3ynokvSQOcDvlPRJWmg0wHfqeiSdFqnA75T0SXptM4GfKeiS9KZOhvwnYouSWfqbMB3DRpJOlNn19JxDRpJOlNnM3xJ0pkM+JLUEwZ8SeqJ2tvwI+KtwDUMbmCemfmLdZcpSXqxWjP8iHgFcDfwwcy8DXh9RFxVZ5lt4jo+ktqk7iad7cA3MvPZavsRYGfNZY6kZJB2HR9JbVJ3wN8GHB/anq/2nRIRuyJiJiJm5ubmaq7O6koFadfxkdQ2dQf8WWDz0PaWat8pmXkgM6czc3pqaqrm6qysZJB2HR9JbVN3wD8CnB8RL6+2rwAO1VzmhpUK0m1ex8d+Bam/ag34mfkd4AbgrojYC3w5Mw/XWeZGlQzSbV7Hx34Fqb9qH4efmQ9k5vWZuafNQzJLBum2ruNjv4LUb51dS2e9VgrSe991ybreq63r+CzVZLXeY5M0uQz4lbYG6VKWa7K68aqL2LZ5E7PzJ7j27iMcvGE72zZvari2kurg0go9sVqTlW37UvcZ8HtipSYr2/alfrBJpydWarLac+/jtu1LPWCG33NtnjMgqazOBHwnFG1Mm+cMSCqrMwHfTseNaeucAUnldaINf3Gn48JQw0nTxNDIrg9HlXRaJzL8rixU5lWKpDpNfMDvSqejQyMl1W3iA35XOh27cpUiqb0mPuB3odOxK1cpktpt4jttu9DpuNJVihOgJJUy8Rl+F3ThKkVS+018ht8FXbhKkdR+I2X4EXFWRFwfEbMRccmi5/5BRHw8Iu6MiOtHq6YkaVSjZviXAY8C3xneGRE/ANwM/GhmZkR8MSL+U2Y+OWJ5kqQNGingZ+YfAUTE4qfeDhzNPNUTeQT4ScCAL0kNWbVJJyLuj4j/usS/n17hz7YBx4e256t9S73/roiYiYiZubm59dV+BC62JqlvVg34mfn2zPwbS/z73RX+bBbYPLS9pdq31PsfyMzpzJyemppaX+1H4DIGkvqmrmGZ9wOXx+m2nu3Af6iprHXb6DIGXhVImmSjjtI5NyL2AH8F2BURPw6Qmd8E9gO/HBEfB36tTR22G13GwKsCSZNspICfmc9k5t7MPDczb8zMLww991uZeVNmfjgzf3X0qpax0WUMXNxM0qTr3UzbjS625uJmkiZd7wL+RpYxcHEzSV3Qu6UVNrKMgYubSeqC3mX4G+HiZpK6oHcZ/ka4uJmkLjDDl6SeMOBLUk8Y8CWpJwz4ktQTBnxJ6onIRePLmxQRc8A3RniLVwF/Vqg6k8Tj7hePu1/WctznZ+aqyw23KuCPKiJmMnO66XqMm8fdLx53v5Q8bpt0JKknDPiS1BNdC/gHmq5AQzzufvG4+6XYcXeqDV+StLyuZfiSpGV0YvG0iHgrcA2DG6VnZv5iw1WqTUR8P7AXuCwz31Dt28TglpJ/ClwM7MvMP26ulmVFxIUMjvkPgR8A/jwzPxoRW4F9wNcYHPfuzHy6uZqWFRFnAZ8FHgVeBlwIvBc4hw4f94KIOIfBsf/HzLy567/zBRHxBWDhZhsnM/OqYr/1zJzof8ArgKeAl1fbnwauarpeNR7vtcA7gZmhfbcC/6R6fCnwcNP1LHzMbwD+1tD2V4DLgbuBv1Pteyfwm03XtfBxnwXsGdr+DPD3u37cQ8f7ceBfA/ur7U7/zoeO+7Yl9hX5zrvQpLMd+EZmPlttPwLsbLA+tcrMg8DxRbt3Akeq5x8HLouILeOuW10y84uZ+ZmhXWcB/4+h46aD33tmvpCZewEi4mwGVzf/nY4fN0BEvIfBsX19aHenf+dDLo2IWyLitohY+G6LfOddaNLZxpkBcL7a1yfLfQbzzVSnPhFxNXB/Zj4REcPHPQ+cGxFnZ+bzzdWwvIh4O/BB4HOZOdP1446I1wGvzczdEfH6oaf68ju/IzMfi4iXAJ+PiOOceewb/s67kOHPApuHtrdU+/qkF59BROwAdjAIfnDmcW8BnulK0BuWmfdn5juA10TEz9L9474aOBERtwJvBH4sIm6iJ7/zzHys+v8k8DCD33yR77wLGf4R4PyIeHnVrHMF8C8brtO4HWLQtPVwRFwKfCkzO5X1VJe2VwIfAF4dEedz+riPMfjeDzVXw/KqTPc1mblwXF8HfpCOH3dm/tLC46qj9pWZ+Ynqcdd/5z8CXJGZ91S7Lgb+HYW+806Mw4+ItzHozJwDnstuj9J5M/APgXcA/4pBxxYMRi/8b+Ai4Pbs0OiFiLgc+H1gptr1PcCvAL8L3MFgwb0LgVuzQ6NVqtFJH2MwOumlwGuBG4G/pMPHvSAifgZ4P4MRSr8C3EeHf+cAEfHXGBzrHzLI5F8KfAj4qxT4zjsR8CVJq+tCG74kaQ0M+JLUEwZ8SeoJA74k9YQBX5J6woAvST1hwJeknjDgS1JP/H8c+ggoIilDiwAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "## Example 3\n",
- "## Scatter\n",
- "import matplotlib.pyplot as plt\n",
- "import numpy as np\n",
- "data = {'a': np.arange(50),\n",
- " 'c': np.random.randint(0, 50, 50),\n",
- " 'd': np.random.randn(50)\n",
- " }\n",
- "data['b'] = data['a'] + 10 * np.random.randn(50)\n",
- "data['d'] = np.abs(data['d']) * 100\n",
- "\n",
- "plt.scatter('a', 'b', data=data, marker='^')\n",
- "#plt.scatter('a', 'b', c='c', s='d', data=data)\n",
- "\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 50,
- "metadata": {
- "scrolled": true,
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEUCAYAAADnQnt7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3XucVXW9//HXGxWvcBKCUhD4GYSmgJeBDnkPvHTopqVoZXG0H2kezvGYqKEiXioktNDyGKkn73ahol8UqYipZCIo4KW4JKJSCaYJKqDA5/fH+o5shrlsZtZiZm/ez8eDx+z1Xd+19vc7M8xnf69LEYGZmVme2rV2AczMrPo4uJiZWe4cXMzMLHcOLmZmljsHFzMzy52Di5mZ5c7BxSqSpGMlzZMUkn4vqUtKP0/S85Jel3RPSjtc0r2tW+LWJ+mzkuZLekLSlXXOnS7pz5LWSXqwJL2dpNGSHpX0oKTHJF0sacdtXgGrKPI6F6tUko4GZgI7RcT6kvRxwNCIODwdC+gYEa83cb8RwIiIOLqgIrcqSS8Cw4HHgDMi4od1zo8AroqI7iVpk4HdgX+PiLcl7QzcCrwTEadvs8JbxfGnD6t6kX2CajSwbCe6A3+NiA3AD5vKLOlw4AvAXhHxNkBErJN0NvBXSTdHxINFFtgql7vFrKpJ6iLpj5KiJG1kSpsh6deS9pN0FHARcFDq/rk+5X2fpCmSHkrXfKnkPrtLulPSk5KmSbpG0j8l3SDpk6mb6feSvp3yLE3X3SDpD+l97pbUsaRcz0u6R9IPJD0t6Q5JfST9VNISSV9tpK4dJN0s6ZHUjXWBMu1LurrukfS/ZX77hgOz67b4IuI1YDbwmTLvY9sht1ysGswoDR5AL+AlgIhYKelUoPYP+x7At4C906fw/wL+NSJ+JGk8W3aL3Qk8EhHjJL0XeErS0oh4CLgM6AQcSvZ/6ffAvIj4anqvTsANwFciYrSkiemeC0vyjANGA5dGxGRJewNnAgcCa4AX09dTgIOB30uaXNoNWOK7wA4RcbikXcm6v/4WEbcDR6fv0akR8XyZ39fewPIGzi1P583q5ZaLVYMhEXF07T/gR43k3QAE8EVJuwHfB+6qL6OkbsAQ4BaAiHgF+DUwImU5GbgrIjambqOf1nObhRHx53T9+SltjaSHJf0eOJUsOJWaHRGvp3suBhakrr0FwB5A13rK2g74fElZ1wA/Bv69ke9FS60t8N5W4RxcbLuS/ugelf4tBX4AdGwge+3A9sqStJUl6XsBr5Sce7Wee2zWpZQmIVwDnB4RRwHjgd3qXLO65PX62uOS1kr7et6nC7BzI2VtjueAvRs41w34SwvubVXOwcW2K5J2Al6OiC8AHyTr1rqmgewvpq9dStK6kLrcgL/VOde5jCIMImvNPJ+OdyrjmnKsBNbRcFmbYwrw4doxoVqS3gMMBG5vwb2tyjm42PamG2mmVBqongfskM6tJrUiJE0BVgD3krrBJHUGPg7UDoj/BPh8WgvSHvh0Ge+/BOid7gVwfAvrA0BEbARuKynrrmTjNOUO3td3zwfIAsz3U/1IX28AboyI+S0stlUxBxerSJKOJRvAhmxA/91FlGR/YPulWVddgNrFlA+SfcJ/Nc2oegg4DBiT7vMAsKOkWcBLqRvqdKB/yjsN+HpEPJzyX0HWLfYE8DPgIbLxHCR9lE2zz0oXcP4y5X1M0s+Bt1KeCZI+l8p+gqSzJY0FDgIukjQ45Ydsxlener4t5wEbJT1Ctv7nLuCOemaLbbE+JaVdBHQpyUsqzzPAzDRG9BDwYEScV8/7m73LiyjNminNPHu7dg2IpNFATUQMb92SFSPNZPsxcHJE/L21y2Ntm1suZs13Kmk2Vlq5fjLwu1YtUYEi4q/AV4HvSarKAGr5ccvFrJkkHULWNbeRbIrwvcAlafzDbLtWWHCRNBQ4iWxQNCLi8jrndwEmki3G6gOMj4hFkrqSDUI+Qjafvz0wKiI2SuoFXEo2KNoL+FpEvFFIBczMrNkKCS5pcdoC4IC0CnoKcENEzCjJcxGwMSImSOqXzh+R+nWH1W6qJ2k+8NWImCVpOjA2ImZLGgV0jYhLc6+AmZm1SFHbvwwGlkXEunQ8CxgGzCjJM4w0SycinpI0QFLH1K9bG1j2IOtuWJbWJxwDPF5yz5vIWjKbkTQSGAmw++67H7rffvvlXD0zs+o2d+7cVyKiS9M561dUcOnK5quMV7HllhUN5VkFkPaDOhuYEBEvSdoLWBObmlr13ROAiJgMTAaoqamJOXPmtKw2ZmbbGUnLWnJ9UbPFVgAdSo47prSy80TEPWQtldMk/RvZeoJdJamRe5qZWRtQVHB5FOiZpmdCtlBtmqROJVtJTCPrPiONucyPiFWSjpI0CN5ddbwM2Dci3iFbGDaw9J4Fld/MzFqgkG6xiHhL2QOFrpO0kmxX1xmSJpBt7jcemARMlHQJ2dbdZ6bL1wKjJT1J1rIRm7awOAsYK+k4oAfZimQzM2tjqn6di8dczMy2nqS5EVHT3Ou9Qt/MzHLn4GJmZrlzcDEzs9w5uJiZWe4cXMzMLHcOLmZmljsHFzMzy52Di5mZ5c7BxczMcufgYmZmuXNwMTOz3Dm4mJlZ7op6WJjZduuYY+pPnzlz25bDrDW55WJmZrlzcDEzs9w5uJiZWe4cXMzMLHcOLmZmljvPFjNrwzzzzCqVg4vZNuJAYdsTd4uZmVnuHFzMzCx3Di5mZpY7BxczM8udg4uZmeXOwcXMzHLn4GJmZrnzOhezCuQ1M9bWFRZcJA0FTgJWABERl9c5vwswEVgO9AHGR8QiSQOBc4Engb7A7Ij4YbrmRmC/ktuMioiniqqDmZk1TyHBRdJuwI3AARGxTtIUSUMiYkZJtnOBFyJigqR+wM3AEcBewKSImC1pJ2CFpF9ExCvA3yPirCLKbNZaGmqFmFWyoloug4FlEbEuHc8ChgGlwWUYMAYgIp6SNEBSx4j4VZ17rQfeSa87SLo4pb0J3BgR6wuqg5mZNVNRA/pdgdUlx6tS2tbm+Q/gmxHxejq+E7g6Iq4GegBfr+/NJY2UNEfSnJUrVzazCmZm1lxFBZcVQIeS444prew8kj4H7B4R36lNi4gnSloqDwAfre/NI2JyRNRERE2XLl2aXwszM2uWooLLo0BPSTun48OAaZI6SeqY0qaRdZ+RxlzmR8SqdPxloGtEXCWpn6QPpvRvl7xHH2BJQeU3M7MWKGTMJSLeknQ2cJ2klcCCiJghaQLwKjAemARMlHQJ0Bs4E0DSp4BrgCclfRroDIwCFgFdJI0H3iKbSXZeEeU3M7OWUUS0dhkKVVNTE3PmzGntYlgVaouzvLzOxfIiaW5E1DT3eq/QNzOz3Dm4mJlZ7hxczMwsdw4uZmaWOwcXMzPLnYOLmZnlzsHFzMxy5+BiZma5c3AxM7PcObiYmVnuHFzMzCx3Di5mZpY7BxczM8udg4uZmeXOwcXMzHJXyMPCzKpJW3xuS0MaKquf82LbmoOLGZUVQMwqgbvFzMwsdw4uZmaWOwcXMzPLnYOLmZnlzsHFzMxy5+BiZma5c3AxM7PcObhsI2eccQZdu3blwAMP3OLc9OnT6du3L71792b8+PFNpm9LjZW7V69e9OvXj4MOOoiamppWKJ2ZtVUOLtvIiBEjmD59+hbpGzZs4JxzzuG3v/0tzz77LHfffTfPPvtsg+ltpdy1Zs6cybx585gzZ842LJWZtXUOLk04+uijWbhwIQD/+Mc/6v0EX44jjzySTp06bZE+e/Zsevfuzb777kv79u059dRTmTp1aoPp5Zo/fz5HHnkkH/rQh2jXrh2SuOyyy3Irt5lZY7z9SxOWLFlCnz59AFiwYAH9+vXb7PwRRxzB6tWrt7hu4sSJDB06tMn7L1++nH322efd4+7du/PYY481mF6OtWvXMnz4cG677TYGDRrEpZdeytq1axk3blxu5QaQxHHHHYckvvKVrzBy5MiyrjOz6ldYcJE0FDgJWAFERFxe5/wuwERgOdAHGB8RiyQNBM4FngT6ArMj4ofpml7ApcASoBfwtYh4o6g6LFu2jG7dutGuXdbAW7BgAf37998sz8MPP9yi94iILdIkNZhejvvvv59DDjmEQYMGAdC/f3+mT5++2fUtLTfArFmz2HvvvVmxYgXHHnss++23H0ceeWSL72tmla+Q4CJpN+BG4ICIWCdpiqQhETGjJNu5wAsRMUFSP+Bm4AhgL2BSRMyWtBOwQtIvIuKVdM+x6dwo4EKyYFOIefPmbRZM5s6dy/DhwzfL09IWQPfu3XnxxRffPX7ppZfYe++9G0wvx9NPP71ZC+uJJ57gkEMOybXcwLvl6dq1KyeeeCKzZ892cDEzoLiWy2BgWUSsS8ezgGFAaXAZBowBiIinJA2Q1DEiflXnXuuBd1KgOQZ4vOSeN1FgcJk/fz5r164FYPHixUydOpWrrrpqszwtbQEMHDiQxYsXs3TpUrp168Y999zDXXfdRd++fetNBxgyZAi33XYb3bp1q/eenTt35oEHHgBg0aJF/PznP+cPf/hDruV+88032bhxIx06dODNN9/k3nvvZezYsS26pxWnsV2fvR2/FaGoAf2uQOnH4lUpbWvz/AfwzYh4HXgvsCY29RfVlx8ASSMlzZE0Z+XKlc2sQtZy2bhxIwMGDOCKK65g//3359Zbb23WvU477TQGDx7MwoUL6d69OzfffDMAO+64I9/73vc4/vjj2X///TnllFM44IADGkzfuHEjS5YsaXSQ/bTTTuONN97gwAMPZOTIkdx999107tw513K//PLLHH744QwYMIBBgwYxbNgwTjjhhGa9h5lVH9XXt9/im0pDgDERMSQdnwd0j4jzSvI8nPI8nI5XpTyr0vHngH0j4qp0vBPwBrBLRISkQ4CbImLz/p46ampqornTZHv37s2TTz5Jhw4dmnV9EZ5++mluueUWrr322tYuSlXZnp/n4paL1UfS3Iho9gK2orrFHgV6Sto5dY0dBtwgqROwPgWQaWTdZw+nMZf5JYHly8AeEXFVOrcuDfbPBAYCs9M9pxVUflavXk27du3aVGABOPDAAx1YWmB7DiJm21IhwSUi3pJ0NnCdpJXAgoiYIWkC8CowHpgETJR0CdAbOBNA0qeAa4AnJX0a6AyMAhYBZwFjJR0H9ADOoyAdOnRg0aJFRd3ezKyqFTYVOSLuA+6rk3ZByes1wDn1XDcV+JcG7vk8cEauBTUzs9x5hb6ZmeXOK/StKnlsxax1ueViZma5c3AxM7PcObiYmVnuHFzMzCx3ZQ3oS/pkPXt+mVkVaGjyg1fuW0uU23K5RNIESc17UpaZmW1Xyg0uXwLGAUdK+r6kTxRXJDMzq3TlrnPZAdgArAM+QrZv2HHAwxHxk6IKZ2ZmlanclssdwLNAf+CUiPh4RIwC3E1mZmZbKLflshD4ckS8+/wVSe2BPQsplZmZVbRyWy6/qg0skg6SdG1EvJ1aL2ZmZpspN7h8oPZFRMwDNhZTHDMzqwaNBhdJ/yVpKfDfkp6TtFTSYrzhpZmZNaLRIBERk4BJkk6OiJ9uozKZmVmFK6tbrG5gkTS8mOKYmVk1aLTlIumuiPhc6hqL2mSgI/DjogtnZmaVqamxk3Hp67URcX1toqSzCyuRmZlVvEa7xSJiUfp6fZ1TTxZWIjMzq3hNdYvdUl8y0A+oKaREZmZW8ZrqFtsI3F5P+ukFlMXMzKpEU8Hl3Ih4o26ipFcLKo+ZmVWBpoLL0cCvJY2tk34kMLSQEpmZWcVrap3LwPT1YGBZyb9/FlkoMzOrbE2t0L8svfzPiHixNl3SjEJLZWZmFa3cjSvbSfqJpKcl/QTYqchCmZlZZSt3A8pJwF3AEqAvcD3w8aIKZWZmla3c4DKv5HHGT0jq19QFkoYCJwErgIiIy+uc3wWYCCwH+gDjaxdtSuqdzq2PiM+WXDOObJJBrW9ExH1l1sHMzLaRcoPLS5L2jYjnJO0LvNZYZkm7ATcCB0TEOklTJA2JiNKxmnOBFyJiQgpWNwNHpHMfBn4DHFf33hFxdJllNjOzVtLUCv1XyWaGCbhYUrBp48pvN3LpYGBZRKxLx7OAYUBpcBkGjAGIiKckDZDUMSJWRcSdkkY0UKaLgXXADsD1EfFWE3U0M7NtrKmWy39ExF11EyV9ronrugKrS45XpbRy8qxq5L4/BZ6PiDclfZVs7OfMeso3EhgJ0KNHjyaKamZmeWtq48otAkuypon7rgA6lBx3TGlbm6dueZ6JiDfT4QPARxvINzkiaiKipkuXLk0U1czM8lbWVGRJQyTNrn3UMXBTE5c8CvSUtHM6PgyYJqmTpI4pbRpZ9xlpzGV+RDTWakFSaVdcH7LZa2Zm1saUO6B/GnA8WVfTNcD5jWWOiLfSM1+uk7QSWBARMyRNAF4FxpNNb54o6RKgNyXdW5I+BXwC6CvpgoiYkE6tlzSJrIXTDzinzPKbmdk2VG5wWRgRr0naMSLWS9qzqQvSFOH76qRdUPJ6DQ0Eh4iYCkytJ/3rZZbXzApyzDH1p8+cuW3LYW1bucHlKElzgV0k3UTWJWVmZlavcoPLcLJnu/wR+DKNT0M2syrQUAvFrBxlBZc09fdjwAHAsxGxsNhimZXHfwDN2qaygksaRK+dnTVU0sciYlShJTNLHEDMKk+53WI7RsS/1R5I+mFB5TEzsypQ7pb7z9U5frHeXGZmZjS9t9gt6eU+ae3Jc8AHUtoVRRbMzMwqV1PdYhuB2+ukCfhCMcUxM7Nq0FRwOTci3qg9kNQ5Iv4haU7B5TIzswrW1MaVbwBI+oikF4GlkpaRbb1iZmZWr3IH9L8EHBoRHcke5LXFNvdmZma1yg0uiyNiBUBE/B3vRmxmZo0od51LX0knsWm2mPcWMzOzBpUbXMaSbbXfH5gHjC6sRGZmVvHKDS6jgasjYn6RhTEzs+pQ7phLH2BBkQUxM7PqUW5w+SMlz7uXdG4xxTEzs2pQbrfYSOBiSS+n447Ad4spkplVosZ2r/ZTKrc/TQaX9ByXJRHRsyTN61zMzKxBjXaLSboOuBB4n6ThtekRcXPRBTMzs8rV1JhLu4g4GjgI+EjxxTEzs2rQVHCpXZW/HvhHbaKkE4sslJmZVbamxlyOl7RHev2Rktf/CvyiuGKZmVklayq4vA28mV7fV5L+TjHFMTOzatBUcLkgIh6vmyjp0ILKY2ZmVaCp57lsEVhS+txiimNmZtWg3BX6ZmZmZXNwMTOz3Dm4mJlZ7srdW2yrSRoKnES2ViYi4vI653cBJgLLyXZdHh8Ri9K53unc+oj4bMk1nYDxZA8t6wOMiYiXMTOzNqWQlouk3YAbgf+OiHFAf0lD6mQ7F3ghIr4FfAco3VLmw8Bv6rn1N4H7I2I88EuyAGRmZm1MUS2XwcCyiFiXjmcBw4AZJXmGAWMAIuIpSQMkdYyIVRFxp6QR9dx3GPCNknveWt+bSxpJtpMzPXr0aGldbBtpbFddM6ssRY25dAVWlxyvSmlbm6ex+64C9pS0RYCMiMkRURMRNV26dNmqgpuZWcsVFVxWUPJwMbLnv6xoRp7G7tsReC3te2ZmZm1IUcHlUaCnpJ3T8WHANEmdJHVMadPIus+Q1A+YHxGrmrjvu9fU3jPfYpuZWR4KGXOJiLcknQ1cJ2klsCAiZkiaALxKNuNrEjBR0iVAb+DdB5BJ+hTwCaCvpAsiYkI6NQa4WtIHgQ8A5xdRfjMza5nCpiJHxH1svtklEXFByes1wDkNXDsVmFpP+qvA/823pGZmljcvojQzs9w5uJiZWe4cXMzMLHcOLmZmljsHFzMzy11hs8XMzGo1tLXPzJnbthy27bjlYmZmuXNwMTOz3Dm4mJlZ7hxczMwsdw4uZmaWOwcXMzPLnaci2zbnJ05aLU9Rrl5uuZiZWe4cXMzMLHcOLmZmljsHFzMzy52Di5mZ5c7BxczMcufgYmZmuXNwMTOz3Dm4mJlZ7hxczMwsd97+xQrjbV7Mtl9uuZiZWe4cXMzMLHcOLmZmljsHFzMzy11hA/qShgInASuAiIjL65zfBZgILAf6AOMjYlE69wXgYGAD8JeI+EFKvxHYr+Q2oyLiqaLqYGZmzVNIcJG0G3AjcEBErJM0RdKQiJhRku1c4IWImCCpH3AzcISk7sD5wMEREZIel/RARCwG/h4RZxVRZjMzy09RLZfBwLKIWJeOZwHDgNLgMgwYAxART0kaIKkjcDwwNyIi5XsU+BiwGOgg6WJgPfAmcGNErC+oDmbWSvyEyspX1JhLV2B1yfGqlFZOnsauvRO4OiKuBnoAX6/vzSWNlDRH0pyVK1c2uxJmZtY8RbVcVgAdSo47prRy8qwAetdJXwIQEU+UpD8AXAhcWffNI2IyMBmgpqYm6p63/HihpJnVp6iWy6NAT0k7p+PDgGmSOqWuL4BpZN1npDGX+RGxCvgdcKgkpXyDgd+mfN8ueY8+pKBjZmZtSyEtl4h4S9LZwHWSVgILImKGpAnAq8B4YBIwUdIlZC2VM9O1L0maCHxH0gbgpjSYD9BF0njgLaAvcF4R5Tczs5bRpnHz6lRTUxNz5sxp7WJULXeLWVvhwf58SZobETXNvd4bV1pZHETMbGt4hb6ZmeXOwcXMzHLn4GJmZrlzcDEzs9w5uJiZWe48W8zMqoL3I2tb3HIxM7PcObiYmVnu3C1mm/FiSTPLg4OLmVU1j8W0DneLmZlZ7hxczMwsdw4uZmaWOwcXMzPLnYOLmZnlzsHFzMxy56nI2ymvZzGzIrnlYmZmuXPLxcy2S15cWSy3XMzMLHduuZiZlWhsPNKtmvI5uFQBN+/NrK1xcKlinhFmZq3FYy5mZpY7BxczM8udg4uZmeXOYy5tkMdKzCrL1v6f3R4m2xQWXCQNBU4CVgAREZfXOb8LMBFYDvQBxkfEonTuC8DBwAbgLxHxg5TeC7gUWAL0Ar4WEW8UVQczs1Lb4oNftcz+LCS4SNoNuBE4ICLWSZoiaUhEzCjJdi7wQkRMkNQPuBk4QlJ34Hzg4IgISY9LeiAiFqd7jo2I2ZJGAReSBZuK49aJmVWzoloug4FlEbEuHc8ChgGlwWUYMAYgIp6SNEBSR+B4YG5ERMr3KPAxSc8DxwCPl9zzJloQXPwH3sxaQ3P+9lRa11tRwaUrsLrkeFVKKydPQ+nvBdaUBJ367gmApJHAyHS4TtLTzahDpXgv8EprF6JA1Vy/aq4buH6tSmrxLfq25OKigssKoEPJcceUVk6eFUDvOulLyH6Iu0pSCjD13ROAiJgMTAaQNCciappflbbN9atc1Vw3cP0qnaQ5Lbm+qKnIjwI9Je2cjg8DpknqlLq+AKaRdZ+RxlzmR8Qq4HfAodK7cXcw8NuIeAeYCQwsvWdB5TczsxYopOUSEW9JOhu4TtJKYEFEzJA0AXgVGA9MAiZKuoSspXJmuvYlSROB70jaANyUBvMBzgLGSjoO6AGcV0T5zcysZQqbihwR9wH31Um7oOT1GuCcBq69A7ijnvTngTO2siiTtzJ/pXH9Klc11w1cv0rXovpp0/i4mZlZPrz9i5mZ5c7BxczMcld1e4tJ2hV4DLg3Is5vbJuZSiOpL3AasAY4ChhHNh27KrbEkTSarA6vkP2szgR2JZsA8lxKGxMRL7dWGbeGpPcDVwEDImJgStvqbY/aqgbqdyHwfuDvwKFkO2r8OZ2r+PqVnPs82bhwh9r/b01tedWWNPCzEzAqZekFvCcizkjnRpMt/9iT7G/rr5p8k4ioqn/ANcCtwMR0fBFwQXrdD3i4tcvYzHrtQDb1ul063gvoAkwHBqW0UcCVrV3WZtbv/WQzCWvrNxX4PNmWP6ektE8At7d2WbeiTp9NZZ5Tklbv7yPQHZjHpnHQx4E+rV2HZtTvypI6DAf+XzXVL6XvD3wDCGCPlLYb2Qe8ndPxFGBIa9dhK392pwNfLDnun75+GPhNer0TsJgs8DT6HlXVLSbpdLJtYZaWJA8jW3dDRDwFDChZa1NJBgICRkn6Otkvxj/ZckucYa1TvBZ7C3ib7NMRwB7AM5T8/Kiw+kXEz9h8twlo+Pex3m2PtlVZm6O++kXEpSV1aAfUtqKron5p38QLgLqtkoa2vGqTGvjd/DzQSdJ/Svomm352H2fT7+w7wJ+AI5t6j6rpFpP0IWD/iBgjqX/JqYa2k1m1LcuXg55kv8CnRcTrku4AOlPmljhtXUSsSk3vH0v6G/AS2SfB0p/fKmBPSTtGxPpWKmpLbe22RxVJUnvgS2xablAt9fsGWe/A29p8f5VqqF9PoGNEXCHpg8B0SfuT1eNPJfnKqlvVBBfgRGCtpIuAw4H2ks6lvK1oKsEq4M8R8Xo6fgQ4gjK3xGnrJB0EjAYOiYj1kq4BxrLp5/dPsvq9VsGBBbZ+26OKkwLL/wAXR8RfUnLF10/SPmRjDqeUBJbzJP2G6vg7s4psvJqIWJRa1PvQzLpVTXCJiG/Uvk6DpntExHfT68HAw3W2mak0jwGdJe0QERvIPmU8Q9Z6GQjMprK3xOkGvFoSOP5GtgtD7TZBL1LZ9atVW5/Nfh8l/Y6sy7P2g8Jg4PrWLGhzpAk1N5CNeT4j6TMRMYVsW6eKrl9EvAiMqD2W9C3g2oh4I3WX9ZS0c+oaO4zs+1BJZgD7AqTAsgPZxIxfA5el9B2BDwEPNXWzqltEKekzZE3x9sD3gV+Szc75G9knp29G5c4WOxH4KLCS7A/vKOB9ZJ/wn0tp50UFzhaTtANwHbCWrJVyINkzf9YBVwPLgA8AF0XlzBY7CvgicALZJ/lr0ql6fx/TbKoastlUi6Ltz6aqr353kv3s/pqy7R6bZiNVfP0iYo2kLsBXyCYvXAn8ICKWSzqWbKB8JfBOtO3ZYvX97NoDE9j0f21KRPwm5R9N1mrbk2yvxyZni1VdcDEzs9ZXVbPFzMysbXBwMTOz3Dm4mJlZ7hxczMwsdw4uZmaWu6pZ52K2rUk6CxgAvEy2PuCvEXFRAe/zaWBeZA/LM6sIDi5mzZAWmV0JdI2ISIvLvlfQ232abO3P8wXd3yx3Xudi1gySdibbNv9bwK0R8UpKH022mvmhUZD2AAABl0lEQVRrwFCyxyM8SLbBaCfgkxGxQdKVZIvW3gZ2iYjRkvoA/0u2wHIpcDLZzsKTyXYU/jMwiSyILSXb3+mhtAmhWZviMRezZkhbfBwFHAT8SdIjkk6IiG+TPY/m/og4GehPtlvu6cD6lB+yrc4vjIhLgb6SDoiIxcBN2e3jArLgtIgssPwoIsYDfdM9bgDOx60Za6PcLWbWTBHxDHB62rrmJGCKpB7pXO2Gjf8Eal+/xqYNANtLmkD2DJtuZM/mqfWn0nuU7r4bEfMk/Q/wM7JWz5j8a2bWcm65mDWDpF6SbgZIG4n+gmwftHKufQ9wO3BJao0srJOlbl/1huwy9U6bXf4xIj5KtvHjuObXwqw4brmYNc/rZLtUfye9/j/AhWQbi/6LpBFkGwD2BEZI+hVZF9npZA9e+glwm6Q5ZLvMni7pT2QPgdtT0pCImJHe637gy2QfBscDX5f0JNlGpW1680fbfnlA38zMcuduMTMzy52Di5mZ5c7BxczMcufgYmZmuXNwMTOz3Dm4mJlZ7hxczMwsd/8fgMZUXTs0SD8AAAAASUVORK5CYII=\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "## Example 4\n",
- "## Histogram\n",
- "import matplotlib.pyplot as plt\n",
- "\n",
- "mu, sigma = 100, 15\n",
- "x = mu + sigma * np.random.randn(10000)\n",
- "\n",
- "# the histogram of the data\n",
- "n, bins, patches = plt.hist(x, 50, density=1, facecolor='b', alpha=0.75)\n",
- "#n, bins, patches = plt.hist(x, 50, density=1, alpha=0.75,histtype='step')\n",
- "\n",
- "plt.xlabel('Smarts')\n",
- "plt.ylabel('Probability')\n",
- "plt.title('Histogram of IQ')\n",
- "plt.text(45, 0.020, r'$\\mu=100,\\ \\sigma=15$')\n",
- "plt.axis([40, 160, 0, 0.03])\n",
- "plt.grid=True\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 5,
- "metadata": {
- "slideshow": {
- "slide_type": "skip"
- }
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "Data has been generated!\n"
- ]
- }
- ],
- "source": [
- "### Parse files and get data\n",
- "### Backend -- Not a plot!\n",
- "\n",
- "import pickle\n",
- "import random\n",
- "import csv\n",
- "import glob\n",
- "import numpy as np\n",
- "from matplotlib import pyplot as PLT\n",
- "\n",
- "## Folder containing raw data\n",
- "folder=glob.glob(\"data/download/*\")\n",
- "\n",
- "### Read data from files and create a dictionary holding the information\n",
- "### output is dictionary containing lists\n",
- "dictYear = dict()\n",
- "for file in folder[:] :\n",
- " filename=file.split(\"/\")[-1]\n",
- "\n",
- " with open(file, 'rt') as f:\n",
- " lineData = list()\n",
- " reader = csv.reader(f, delimiter='\\t', skipinitialspace=True)\n",
- " cols = next(reader)\n",
- " for col in cols:\n",
- " # Create a list in lineData for each column of data.\n",
- " lineData.append(list())\n",
- "\n",
- " for line in reader:\n",
- " # column 1 and 2\n",
- " for i in range(0, len(lineData)):\n",
- " # Copy the data from the line into the correct columns.\n",
- " lineData[i].append(line[i])\n",
- "\n",
- " data = dict()\n",
- " for i in range(0, len(cols)):\n",
- " # Create each key in the dict with the data in its column.\n",
- " data[cols[i]] = lineData[i]\n",
- " # add the list to the dictionary\n",
- " dictYear[filename]=data\n",
- "\n",
- "\n",
- "### Get information of the loaded structure\n",
- "\n",
- "#### Get categories. X axis\n",
- "season_samples=len(dictYear)\n",
- "\n",
- "## Different classes. Number of cores\n",
- "seasons = []\n",
- "ucores = []\n",
- "for key, value in dictYear.items() :\n",
- " seasons.append(key)\n",
- " new = dictYear[key][\"Cores_per_Socket\"]\n",
- " ucores = list(set().union(new, ucores))\n",
- "ucores=[int(x) for x in ucores]\n",
- "\n",
- "ucores.sort()\n",
- "seasons.sort()\n",
- "\n",
- "\n",
- "## Create a Matrix of = Seasons * unique_cores\n",
- "hpc_core = np.zeros((season_samples,len(ucores)))\n",
- "## iterate over the structure and get cores per year.\n",
- "x=0\n",
- "for season, content in sorted(dictYear.items()) :\n",
- " ### iterate over unique core list\n",
- " y=0\n",
- " for core in ucores[:]:\n",
- " list_values=dictYear[season]['Count']\n",
- " list_cores=dictYear[season]['Cores_per_Socket']\n",
- "\n",
- " if str(core) in list_cores:\n",
- " # get index\n",
- " index=list_cores.index(str(core))\n",
- " hpc_core[x][y]=list_values[index]\n",
- " y+=1\n",
- " x+=1\n",
- "\n",
- "hpc_core_acum=np.cumsum(hpc_core,axis=1)\n",
- "\n",
- "file = open('data/top500.pickle','wb')\n",
- "pickle.dump(hpc_core, file)\n",
- "pickle.dump(hpc_core_acum, file)\n",
- "pickle.dump(ucores,file)\n",
- "pickle.dump(seasons,file)\n",
- "file.close()\n",
- "\n",
- "print(\"Data has been generated!\")\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 51,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": [
- "## Example 5a\n",
- "## Stacked area plot A\n",
- "import pickle; import numpy as np; import matplotlib.pyplot as plt; import random\n",
- "## Read filie to obtain data and labels\n",
- "file = open('data/top500.pickle','rb')\n",
- "hpc_core_data = pickle.load(file).T ## samples\n",
- "hpc_core = pickle.load(file) ## stacked data\n",
- "ucores = pickle.load(file) ## labels\n",
- "seasons = pickle.load(file) ## time \n",
- "file.close()\n",
- "\n",
- "## ...continues"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 221,
- "metadata": {
- "scrolled": true,
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeoAAAGsCAYAAAASbORLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsvXecJFd59/t9qqrzdPfkvLuzebXS7kpCWkUUAQkkwBhsMpIj5vq9fv3ahut0ba4/GNuAbXDAIJIwwRgMBiFMFAhJCEkIpN2VtKvNeXfyTOfuCuf+0TVSazQzO6Fnumf2fOfTn6k6Veecp+KvTnqOKKXQaDQajUZTnxi1NkCj0Wg0Gs30aKHWaDQajaaO0UKt0Wg0Gk0do4Vao9FoNJo6Rgu1RqPRaDR1jBZqjUaj0WjqGC3UGk2VEJE1IvINEXlARO4TkftF5HcXIZ+viUhBRG5YYDp/JiJnReS91bFMo9EsBlqoNZrqcTfwXaXUdUqpm4H3Ar8zsVFE7q6GKCqlfhk4W4V0/hr4zkLT0Wg0i4sWao2meuwE7p9YUUrdD3yhVsZoNJqVgRZqjaZ6HAPeIyKxiQCl1N8CiMj/Bm4F7vSrxH/DD/+oiDzsh/2HiCQm4orIehH5toj8WER+OlVpXERMEXlCRM6IyMcr4n3Pj/egiFw9Kc0H/fQ+A0SmOxgRaRCRz4nIQ36cfxMRy9/2F361+T+LyBdF5KiI3O1ve4eIPOLn/8WJY5opPY1GMz1aqDWa6vF/A68GTonIZ0Tk+okNSqmPUK5mvlspdYNS6lP+pmeVUlcrpW4AngXeDWUBBr4JfEkpdT1lkf/NKfKMA4eAK5VS7/Tj3VsR73eBe0Qk7u//ReB/lFJXAX8OvHyG4wlSrsq/Vin1Usqifod/PH/lH88Nvl07gIMicg3wD8Cr/fxP+eszpqfRaKZHf81qNFVCKXWfiKwG3gy8FfiRiHxCKfXOGaLlReRBwAM6gMN++JXABvyqc6XUuIi8cVLcBGVRvkMpdawi3nrgc3683SJyCrhdRB6mXD3/Bn/bKRF5aAbbRoE1/j4O0AfkgE9V7PMDpVTOX36fiHwC+KZSatAP+yLwsIj81izT02g0k9BCrdFUEaVUFvgk8Em/RP1DEfmAUurQ5H39Xtt/D2xTSh0VkTuBO/3NvcCoUsqpSPsnk5L4S8ql0lcDH66Ip4Dvi8jEfiEgCXT560MVaYzMcDh3AO8ELlZKjfhV732T9hmftN4LbBWR+/11C+gHWoDbZ5GeRqOZhBZqjaZKiMi/KaXeNbGulPqxiAxTLvlOxU7KVd9H/fVAxbYTQKOIWBNiLSIXAEeVUnl/n/8XGADuE5Fv+h8DJwDbr0qfsCtGucTe7ge1Acf95RZgIv+p7HtMKTUh5oFp9qvkBHBYKfXcsDQRaVVKDYnIfNLTaM57dBu1RlM9XuaLEQB+iVoB+/ygNBAVkZiIfAE4CGwQkRZ/+y0VaT1Kue35LX5azcCXKVcZT5BTSj0O/BvlErz48Y6LyC/78Szg68Amv3r8MeDt/rYe4Hqm5yCwQ0RCfjo3z+Ic3A3cJiJNfh6bKbe1zzc9jea8R/R81BpNdfDbYd9GufRq+v//WCn1iL/9KuAzQIpyVfWXgLsod8jaDWSA1wB3KaXeIyLrgX8BopQ/qv/cL6X/O/CrlD8A3kK5s9YtwM+A1wFh4F8pV4sbwGeUUp/2bVgPfJZybdoRytXilwLvV0rdNel4YsDngS3AU36cq4AP+Lu8BygAX1ZKvaci3tuA/0W5/bkE/J5Sav9M6SmlJjqcaTSaSWih1mg0Go2mjtFV3xqNRqPR1DFaqDUajUajqWO0UGs0Go1GU8doodZoNBqNpo7RQq3RaDQaTR2jhVqj0Wg0mjpGC7VGo9FoNHWMFmqNRqPRaOoYLdQajUaj0dQxWqg1Go1Go6ljtFBrNBqNRlPHaKHWaDQajaaO0UKt0Wg0Gk0do4Vao9FoNJo6Rgu1RqPRaDR1jBZqjUaj0WjqGC3U5yEicr2IfF9E7heRB/3lO0QkWGvbFhsRucE/5vtF5AERuUdEXr7AND8qImMicmeVzFxUROQvROSsiLx3AWm8RUQ+WUWzqo6IvF1E9olIUUTuqwj/gH/8/SLyYT/sPhEpiMiz/r2xR0T+U0RaKuK1isjHReQnIvJjEXlERN4nImtqcXya8wdRStXaBs0SIiK3Ah8HblZKHfTDXgncA1yulHqylvYtJiKSAI4ANyil9vhhfwm0KaX+1wLTvh+4Wyl19xzjvRfoU0rduZD854qI3A0cVUq9dxb79gFHlFJSEWYCEaVUZpFMrAr+x9P7lFK9k8LvBiyl1Nsqwo76+35SRALA94FTSqm3ikgD8BjwL0qpj/r7twPfAR5QSv3+EhzHnUqpGxYzH019okvU5xEiYgAfBf56QqQBlFLfBv6rZoYtHZsBd0KkfT4G/LxG9ixblFJuvYv0QlBK2cBXgVv9oD8CxiZE2t9nAPiTGpinOc/QQn1+cSmwFvjeFNt+HZgoZXaIyFf9quFHROQOP3y1v65E5E4R+aGIOCLSJyLtIvI1P87DIvJLEwmLyG/78e4TkXtFZMvkzEXkNX415UMi8jG/evFxEbm0Yp/1IvI9v9rxQRG5elLcH4vIB0XkCRE5MsUxngRaRORd/kcLSql+pdRnKvK43E/nAf//5RXb2kXkK/62n4rIP4pIZIpjuUdERkXkGxXxXnRuROSNwJ3ArX51659NddFE5CUV9twnIltEJCgiu0UkLyKf8ff7AxEZqqjOvdXP7wER+a6IbJgm/X/3q31v8Ne/4V/jPhFJAl/yw+/3fztE5Em/BDqRxmzumTtE5AdSrl6+eipb/DgbReQ7FefrVj9850S+IvJu/3zsFpFN06W1QAKA7S+/gamfm+8D01231/r3yX1Sbl66yr/30iKyV0SuFZE2EfmFiBwRkW1TPSsicj3wx8DF/vn/Zz/96e6ryefpJyLymH89P+afs89W2LlFys/yD6X8XN1ZvVOoqQpKKf07T37AGwEFBM6x3w+A9/rLrcAZ4Dp/vc9P4x3++h8CXZRfYn/lh3UBw/6+Df5yyN/2vylX4U2V752AA2zz198CHKX8wjSBvcCv+9u2A0NAvCJuDtjir39omjzeTfnlexT4ALCxYlvST/MGf/1af73RX/8e8Jf+chD4BeVqa4D7fRuCwOeASyrSnfLc+OvvpVxlPt21SAKDwE3++m3As5Q/sluAPNDrb7OAr/nL64AMsMlffxuwj3J1L8DdE9fYXz86cdz+uqqwsQ9Qk+y6gXLV+VzumV/1198DfHea47V8O+/019cDKWB9Rb4l4Fp//aPAx2c4f3cCRf/6VP7OAp+ftO9R4DcrzvuTwL/663ngt+b4vA0AHf7yayvOzz8Bd1Xs94fAjczwrPjHcf+k9Ge6rybO05X++teBx/3jCvm2TWz7MvBGf7kT+PZivYP0b36/mhugf0t4sWch1ECPv8/qirBPAJ/2lydeuskp4qypCPsG5WrBCGWx+y0g6r+Ig9PkfSewq2Ld9F821wHX+MuBiu27gDdXxH1iluehF/hTysLvAG/zw98KHJ607wHgHdOcl4uBmL98v3+M9+AL1LnOjb/8XmYW6rdSbh+uDBsHrvKXv16R1u3AO/3lPwN+OOlc5nlePO+mSkI9h3sm4a/fCuyf5ngnrrNVEfZ94C8q8h2p2PY7wPdmOH93AienCL+bqYX6Wf9aPgZ8kHI7PMxPqPcBfw40Uv6wCvvhlwGjFev3+tunfVaYJNSzuK9uAIYrtr0P+GrF+kPAW/zljwFfqbje0bkcp/4t/k9XfZ9fTLRL98ywz0Snm8GKsMGKcACUUuNTxPn3iepRyiWhmFIqD1zv/45Q7siWmCH/0Yo8XGCMcmmhl/KL6fsVeYQolxAmqLRpWpRSJ5VS71dKXQD8f8D7K45jcNLuE8f+ovOilHpSKZWt2PfdQAfwyxVh056b2djqx2+uqHa+37dhojfyv1P+kAD4VeA/pzoW/1yOMuk6VonZ3jMpf7FAueZhurRGlVLODGmlKpZnSms+fFApdYNSaqdS6t3+/QvlZ2em52YqXu7H2Uf5unQBKKUeB04DrxGR7cBTSilvjs/KbO6rdMWyM8X6xHn7P5Q/en8oIg8BV87xODWLjBbq84snKJcQXzF5g4h8SsrtwSf8oLaKzW2U23enYyLOG/yX3A2USw1/K+Xes/2q3Lt2E9AM/P0MaTVX2GRRLo2c8fOwJ9L383gJ8NkpU5kCEemZoh34qzwv9id44XHD88f+ovMiIutEpKli3w8DvwLcWdEGO+25maXZJyiXCCuP+1Keby+9F2gXf4iZUmpsqmORci/tJqa/jiXKHz6ISOMsbau0EeZ2z8yUVpN/7ReaVjX5T6Z+bl4vIn8+TRxHKfUuyv1CBiiX4if4HOUPrHf4y8zxWVnofVVJo1LqfZSF/uPAN0Vkth+SmiVAC/V5hFLKA34b+JPKjkUi8mvANuBJpdRpyiJwp7+thXKV6mdmSHciztsrgj9Gud2th3I16EQp/EnK1bDTsUlEtvnLb6Jc8vgp8ChwXER+2bfLolztO5eORAHg16VibCzlTkIP+Mv3AnERuc7P42rK4nbPFOclRLltr7I0l1NKHafc8efTIhI+x7mBciknKmX+ewqb76XcAe5yP98Y8CP8jwulVImyiNxNufpygv8ALqu4zm8EjgEPT3NujgAX+cuvmrQt7ecdFZE/FpEXlLjmc8/MwKOUS69v8dNaB1wBfGEeaVWTf6B8nd41ESDlYWvvB747TZx7RcT0S8qP8cL7/vOUS9zblFJP+2EzPStpytXhiMhXKQv/TPfVXPiMiHQopRTlZyFAufZKUy/Uuu5d/5b+B7wU+CHlh/Ih4FNAa8X2dsrDtR4AHuH5Di3N/rqi3I63dYo4D/q/P/XDY376D/npfY+KtsxJdt0J/JhyyfQhysOmXlKxfT3lcas/9vOY6Fh2E+XqxTFmbq+MAn9NWfh/5P//T6CrYp+X+Mf2gJ/PzknH+BV/28OUSzNQ7pQ25ttwE3AX4AG7/fSmPDd+3A3A074t757G7gmbfuznffuk7VdQfnFbk8JfAfzEj/Nd/I5zwF9Q7kx1FPgNP+xayu2zPwDu8K/xI0CPv/0L/vX4Pv5HHeVq56/M4Z75BrC6Iu6/T3O864FvV5znV/rhWyvifhzYWXHdPzBFOm/3txeB+yrCP+Affz/wYT/sPj/dZ4G/mcauZspCOnH/3EdFu/4U+/+Db//9/nXfMWn7D4D/U7E+7bNC+YPxF/71/Mg5nrnJ5+k1/rU+C7zLv/6V9+sdfro/pNzh7I21fkfp3wt/2uGJpm4Q7dRBcx4hIl8E/kApdbbWtmjqG131rdFoNEuEiDSLyG1+80BQi7RmNmih1tQFIvIannfq8M+1tkejWSRCwL9RbsL5uxrbolkm6KpvjUaj0WjqGF2i1mg0Go2mjtFCrdFoNBpNHWOde5fFp7W1VfX19dXaDI1Go9Foloyf//znQ0qpyU6WXkRdCHVfXx+PP/54rc3QaDQajWbJEJFjs9lPV31rNBqNRlPHaKHWaDQajaaO0UKt0Wg0Gk0do4Vao9FoNJo6Rgu1RqPRaDR1jBZqjUaj0WjqGC3UGo1Go9HUMVqoNRqNRqOpY7RQazQajUZTx2ih1mg0Go2mjpmVC1EReQQo+KuuUupmEWkG/hY4DGwE/lQp1e/v/24gATQB31NK3VN1yzUajUajOQ+Yra/v7yil3jsp7P3AD5RSXxaRVwMfAt4uIlcANyqlXiUiAeAZEXlAKTVWPbM1Go1Gozk/mG3V9zYR+X9E5L0icpsfdhvwU3/5J/46wO0T4UopG9gLXFclezUajUajOa+YbYn675RSj4mICTwgImmgHUj721NAk4hYfvjeirgpP+wFiMhvA78NsHr16nmaPzUnCyW+3j9a1TSh/FVjoLAAUyksFKZSGEphKs//rzCUh+F5mMrDVArxXMTzMFz/v/KXXReUwgmFsIMhnECIghWgYFoUTJOCGLiq6oeh0dQNBtCcz9GeyxPPZIiU8ljKwzAsDDExDRPh+f+GGJiYiBgYGAiCYCBKMDBAlUMA1MSfKBSe/1/h4aKUh6vccri/7OHieS6ucvA8pxzmOjjKeS5cghYqGETCFgQsvICBF7BQloFnGniWgWsInmFiY+IqCwfT/xm4mDjKxMbAUYKDiVL6IV8OXJyIcm1TvCZ5z0qolVKP+f9dEXkQuBEYAOLAGOX26FGllCMiE+ETJPx9J6d5F3AXwGWXXVbVOzVw5gRtn/tUNZMEwAwEsRrimNEYRjCMCgbxxMRRUHJdcrZdtYdOgDCgIlG8cBQnHMYJhbEDIUqBIAXTIm+Y5AyTLEJGgT2HrIXyxTcFAoAJWFL+CLEA0/8IMZXyl6FgGBxTJk5VjlCjqUCC0NBEk9tER75ISy5NIjtOKDNOuJjGzKfwMmMox661pbPCCBgEIgaBiEU0LFghAyskmEGFGQAjoDACHoblQtAGI4XnjQNatOuVduOV0PS2muR9TqEWkS3ANUqpCeXbCHwN+BZwFXACuMZfB7gX+Es/rgVsBR6ortnnRhbhK9UrFSmNFGFk6EXbDCCMEIjFsGINGJEoEgjjWRaeGNieoug42M7sZU4Ayecw8rlZfVEpK4AXieJFoihA/BK8uA64LuI6iOeC4yCeN2s7KtlqBSh09TKYbOGoFWZMv1c01UKEUQtG42GIh4E2RClaXKEh72HmHELZDOFcimaVI+5mCZfSGPkUXmYc5dbPJ6RnexRtj2JqdjaZ0U4iHRcTarawYg6BcI5gMItppoAxPC+1uAZrzo3U7mU3m/d/CrhdRLopl45PAP8BfBv4OxHZBKwH/ghAKfWoiPxIRN5Pudf3Hyx1R7KQ67Em3oxjgAs4KBzPK/9cB8excfxq52oiKJxsBiebmXJ7AAiYFsF4AjMaRUJRCIVIOYqSvfCSgjg2ZnocMz2+4LRmyiNy4girTxxhNWA3tZJq7+JkJM4JZTA/+ddopkaJMGTBUNyAeBBoxlRNNDtCQ8FDsja5VInxVJFmq0SnUaBF8oS8UtVtMVDEyBPxigTdPJZbwLVdbMfFtl1s28F13Hml7eZyZI4cJnOkvB5INBJs7cIJrSdrO3iqRCLhEo87hMMFgsEshjkOahRPZat4lJp65JxCrZQ6Dbxuik0jwG9NE+eDC7RrQQguzWdPERjLIoWpH1gFeOEgXjiMFwrhBYO4QQsvEMAxTVzDwDXL7U0O4KIoKUW+VKJUzM9f5F2H0tgIjI08F2SJQWJVH3YswXguP790a0RgdIiW0SFagO2hELnOVQwkmzliBMno0rZmEXBFGAzAYMCAeAg6Q1heHNtRjBQ8RrIObtGteiWyY3sMj1U8nwa0NxRZE87QE8jQbmRokjQxVSDs5Qm4eQzHxiGITQBbBbA9A9szy/9dKDkwmipQmvSeslNj2Kly+cYCgi2tmNLGeCHOyWIJ120EegAIBhWJhEuswSYSLhAIZjCMPOD4P8//74JyUDj+//l9VGiWntl2JltWnG5SfPDmclVRgxumqxSlvRiiNW/RmIN4VhFJlwilCljjGWRs9tVKyjCwW7qxmzsoxuMUwyGKpknRc3DtLE4xQymfwrXn8EWvPHLHDwPQmGzC6uxl3PHmVE1eD0ixSOzYQdYCfYDT1sloaycnQlFOK0O3vmkWDceAgaBA0ISEuWj5tDoNJIdL9J/OUHJcBuwQA3aIn9Ey5f5BUawK5+gNZOgJpGkz0jQzTqc3RoMzSrg0ghEuMB7ooV910Z8NMTSSw7Ff+OyXhocoDZeb3EJiEG7vxEw2UzQtMvkCQ0PC0JAFRChXZM4GhWmCaSpMU/z/PBdmGB6GUV4Ww8M0FKblYpkuhmljGg5i2IiUECkBJaCIUkWUKqDb26vHihTqSjKmzYHIOAciQOOLt4sS2p04naUIbfkATXmTZE7RkHEJp4oEUjmMzPNf0eJ5BAdPEhw8SawiHS8Yxmnro9CyikLyIgpWhKKh8MRGpAAqh+fkcJ0MdiFNKZ9BTdFOXBofpTQ+StC0SK5aSzEcJZ0vvGi/ekeAwOBZ2gfP0g5cEomS6exlINHEYQlQ0M+wZhkyZMFQR5BAWxO9WUXhTJbh8emfz5ISDuVjHMrHgI4XbRcFOxPD3Bg5wKbCU2wO9+N1G4wE1tDvttOfNhkeyb7wXaE8Cv2nof80ABErQLijC4knKWCQmfX7QnBdcF15bv2FLOSDRxEIlEv7wSAEAh6BgIdleViWi2k5mIaDYToYYiPGC8Ue5Qu+LvUDIPUwNOCyyy5Tjz/+eNXS2zu8lw8+Xr3a95Bn0l2KsX20gYt2jWMNz74E7kWTFDvWUWrsJh9uJUuMnB3AdhSBgE0gnAP3OKmhgyh36psy2NKK2d7DWNHGnWaf5YQSodTRzUhzO0dCUYa8yS8IjWb50F5SxIZL9J/J4LgL66WxPTbGzbFDbC09TTx3AgCHAEOBtfTbLfSnYGwsO2PTmxEKEWpuQ4IhJBBEmSbKMHERXKWwPQ/bcZfFu8Q0FaFQWfDLYq+wLAfLUmWxN33BN+znSvdQRHBQVS7RtzRfx+rVb6hqmiLyc6XUZefcTwv13BAFLxvu4iV78oROD887Hae5k1JbH5nGtZy22zFMh3D0NLmx/RQzU48Bl0CQyKq1FAJhMoXlV8qeCmUYDG7ZzmOBBt0RTbOsCXuKrrRH9kyWsXRxweltiGR5RcMhtjlP05g9/Fx5tyQxBqw++ktJ+kddMuncvNIXK4AZiWJFIhjBEARCSCCAZ5h4Uu4Y6ngK23Wwbee8r8jeunUrO3furGqaWqgXSagruXK8jWv3KmKH+heUjt2xlhPrX8V4zkKhiMbHUc5hUkNHYJphVKG2DozWTkYLJbx5DrWqJ0rtXfysZz3Dy/9QNBq6iorwUJGzZzO43sLfsb2hPK+IH+EStZfWzH5EPf+g5MxmBmQV/cUG+kdKFHLV/4hXCFYkjBgWYpmIaSGmiRgmYhqIYYIYYJggghgGyjAQMVACGAblcTGACMpfVpQ/BvJ2/dcWaqFepkI9wdZcEy97NkTTvtMwz4dSiZDa8UqOmRuZuF+tYIlQ5BTZkWcp5dJTxjNCIcKr1pEzA+QKC/+KryXKCnD8govZZYRqbYpGUxViLnSkXFKnM6Ry1Rky1hIocUviGJfLXjoy+zC8Fw7tTFmdjEgHWRUl6wTIOwb5kkKVXOxiiZJdwqtDUTSjUQLxRoxoAwRDuIZJyfPIl+y6KIxooV7mQj3B6mKcVx6K07HnDDLPHttOYwenL3wtw9nIc2EKRSw+gmsfIj10fNr2qXBXD6qxjbF8YVm7JcytWssjLT16eJdm5aAUvUUwBwuc7c9W7flsMF1uSZ5gp7GP3uzTmO70pemxcJyU1YStGig4YQoqTMGzKDkGZglMW8D2cICS52J7LsVSCduxq+5zYi4ohGCsASuRxIjEUMEQjhiUPI9CsYS3RLZpoV4hQj1Bqx3htuPNrNnVj+TnV8rNXHAdxxouoTTJD0ogXCQYPEFm+FnswtRtU2Y0SqRrNU4oRqqQLzt3WWZ4kSj7N+9gv1q8oTYaTS2Iu9A+7jByKkO2UD2XqEFR3Nx4mmusZ1mbfRLTmZ1PBoViONpEfzTJYCCK7YRQRROVF8ycRzSvCDkmliNYJQ+j5KFE8EwDJYIyTTxDUIaBJ/j/BU/AQ1BSHsmtAA+FB3hK+T+PQqlEqTS/96RCCCaSWPEEEo6igkFcDBxPIQIiZc/vz/9U+b8C8MofIEqVPVl6XrkDmuc991Oei/JccD36tl7I9utvnped06GFuoZCPUGDG+C20x1senIIIzV370FeNM7ZHa+nP5988UbxiMaHcAoHyQyfmjaNQChKvKsPryFOyrHJ5JeXF6PU+i08HG+lVPvbVKOpKoZS9OYhdXCMXLG6PhMaLZtfa97NSzIPYjnzf+ZdEYaizfRHEwyEIgwZBqOisG2QAgRKQrJoEi8KDSUhmlOECw6hrIOVLWJmC0jx3FX+bjiI3dREKdFAIRyiYBrkPZdsMY9dqr6Xufmw8cpruOSW26uaphbqOhDqCSzP4NbBTrbvShMYnLs31cL6Sznadi35wtTDmEKRPKZ1jPTQftwZvkwtK0hL10Yk2UgWxVB2FLcO2n7OhZtoZPe6rZxQs52VVaNZPjR4iuSRLIMj1fdKmDRt7mzew2XZBwgsQLCnwxGD0UiSkXCc4WCI4UCQEUMYFo8Rz2bEzSG2oskN0WKHaCwFSJZMGopCrADRvEvTwcFpPUgCuNEIpeZGSg0NFMJBCoaQcx1yhRzOEjqF0kK9woV6AlFww2gHO/eUCJ988cQeM6ECIYYufR2nSh3TNheJ4RFtGKCUO0B29OzMthgWPZ2bMJvayFvCQH6MXLF+3ZcqEYa2bOfRYFwP49KsOEyl6Bu0OXFscfz0x02HO5ufYmfuxwTsqeciWCxyVpjhaIKRcIzhQIgR02JYYASHYa+IW7C5/UQb65/sR3JzqwJ3GqLYTU0UG6IUQkHyBuRdh6JdKtdqS/U+7tdfdgU7XnZL1dIDLdR1KdSVXJ5u46V7hfiBM3OKV+zZxInVryCdn7ntNhAqEQwP4ZbOkBk+jjfDzEIiQlf7JhqaeiiGLIacNEPZ0brskGa3dfKz3vXaSYpmRdKX9Rh4dnTBjlOmo8F0uaP5Ka7M/ZiAPfVIkqXmybZ1fCki5AoFXnOinQ1PzF2wZ0IZBsoKghVCBYIoq/zzrADKtMAM+csBlGH5/02UYZXHlBsWSixaL+hmzc2XVM0u0EJd90I9wWvP9nDxfcfnFEcZBmOX3M5xtXa6YdYvQMQj0pACzpJPnaCYmbn6vaN1He1N6yhGQoySoz83TMGun6FfyrQ4ufVinjDCtTZFo6k6bbZCHUiRyi5e22zUdLmj+Rmuyt9PsFT7KTQdMfh+7wV80xvDsuHVJ9vZ8MQARrZ+HDvFb3kFzW99a1XT1EK9TITaVMKffCeKOTL3h8Vp6eXk5lczmgvOKV4gnCcYGsIpnCYzcnJKn+MTtDQmuSxjAAAgAElEQVT10tO8GQk3kDJLDHtphvNj5SEbNSbfs4ZH2laRrv0trNFUlbCn6DiR58zA4nb+jJoub2/ayzWF+wmWFm963NkyFo7zX51r+GlxgIhr8epTHWx6YvAF8y3UCi3U57FQA7zmTDeX/PDEvOOnt72MY+ELmc+U1mJ4RBpGwTtLbuw4pfz07VcNsWa6WzbSGOrAMwOMB4qMSobhwjjZ4vzcGC4ULxzh4OYd7Fv588tozjeUYv2oy8lDY1X3Wz2ZsOHy9uZnubZwP6HS1C6Ml5LDjd18IRnnSGmUiGtx++kOtvyitoKthfo8F2rLM/jjb4cwx+bfycONN3N22+sYyDUsyJZQNIsVGKKUO0l29MyMjg6ak910Nq+n0WpDeRapcJFRK8tQKcV4LrXoL5dKUus280iiTc/KpVlxrMorxp4dpWgvvj+EsOHx1uZnua54P6HiyKLnNxMKxcNdW/gvs8C4myfiWtx2pp0LnhiZ13DXhaKF+jwXaoDXnelh+w/n1lY9FbnNV3K0cSfF4sI7WxmWSyQ2jGefJTt2HGfGXuFCR0sf7cm1JMxmjKJFKlZiLJBjxEsxnBvHmaFDWzVw40me2nAhxzw9jEuzsmhyIXQwzUhqadpsg6J4a8t+ri/+iHBx/pMPVYO8FeKb3Rv5vj2Ei0fIM7n9TCcX/GIYcwkFWwu1FmqCnsF7vhWsyo3nhSKM7Hg1p5yuWXU2mw0KRTiax7IywDhOaYxidnhaH+RiWHS3baAtvpo4jZh5k0zMZiyUZ4QMQ4UxCqXFmDwARrZs54lwglztb22NpmoElKL3dJFTp5eut3ZQFG9u3s+NpfsJF+c2pLTanG1o4T9bO9lVHCzb5hnc1t/Fhb8YWVBt5GzRQq2FGoDXn+rhovsXXqqewE22MXDhbZzNTeHZrEoYlkswlMW0MihvHKc4SiE9jDNJhIPBCN2tG2mJ9RJzExh5oRBxGY7l2Zc/RrHKvcqVCMXOHgZbOjhkRUjV/jbXaKrC2nGXMwdGl8zHNYAlHq9vOsqVxlNTTgSylOxp6+M/IhZn7XIHXMszuK2/k22/GF1UwdZCrYUagJBn8p57LYx5zi87HaXuDZxZ+zJGsks3K5UVLBEI5TCNFJ4zTqkwQiE98tx47mgkQXfrZlrDPVilEM8mBzg2fnpRbFGA3d7FUGsnR0IxPZWmZtnTVVLknx0jV1g6z1wTxE2HW5In2Wnso+ccE4EsFo4Y3NezhXtUirxXHsZmeQav6u9k+5Pj8xpFcy60UGuhfo5fOdHD1geqV6quJLdxJ6daryCTr00brkIRjBQIWFlE0njOKPn0AB2JVawL72AsUmC3e3TRe5A7zW2MdPRwJBSjX52fjlNMICzlXwhFSCmCyiOoPAKeS9BzsRwHy3UwHQfTKWEZHlaTSTHskpYooyrKmBti1LUonKfnsZYspuvR2RI2PG5OnuZq61lWZ/csipvSmUiFGvhqZx8PlQae67pqKuGasXbWD1m0nckRPjOKOAvviKeFWgv1c0Rciz+611i0YQhKhPS2l3EyvJVZ+MpffMQjFj9KbmgfO9bcRDgX41DzCAfHjy9Jr3E32cRYZy/HowlOerKE/dTnj4UiLEJYFCEgpDyCShFULgHXJeB5WK79nNAadgnTtpFSEcMuIcUisoCOfSLQ0WHT0jKCFTiK541TMpvIGF1kzA7S0kKKRsZpYMyLMOoGGXNN7fp1EVhs16NzsgXF9cl+Xhrcz/r8HoKluc9rMF+ONnbxhWSSQ6UX91QPegYXZZvYNBqmq98mfnJkXp7PtFBroX4Bbzrew+YHF6dUPYEXDDO6/VWcUquoh1kwQ9EsTuEx2mKdrAtuIxO02W0eYyy3dF6TvFgDqe7VnIg1ckwZiyYsBhAVaBBFzC/FBr1ySTbwgpKsjWmXMGwbo1RE7BJSLCB1NpFKa6tDW/sYweAxPG/qHsIKg5zVRcbsIiNtpKSJFElGVZzDdoy8dgm7IPoyHgP7F8/16FwRBVckhrghfIDNxaeIFAaWJN9HOjfxZavEmDt9rZwoWF9McuFYA6sGPJKnxrFGzt1BTwu1FuoXEHUt/vAewcgtftuPG29m8KLbOVtoquXc8GXEI5Y4Sm5wHztW30Qk28Dx1jH2pY8u+SxfXjhCpns1p+JNHMHiXOXPkEAMRQxFVHlEPIeQ6xCybQKlIlapgFnIY+RzSCHPSpWlxkaXjs4U4fAJPG/miWEm8LAYDL2Ew+Y29jldnLYDi2zlyqTVVrDIrkfny47YGDdFD3GhvYeG3PTT8laDohngoc6N7ArAvtIojjp3SaTdjrAtlWTtkEHrmRyhM6NMHjKjhVoL9Yt4y9EeNv5kcUvVldgdfZxZ/wqGc5Ely3M6JpeuC4bDU5FTDGRqM55TBYNku1aTakgQdB2CpSJWqUigWMDI58riu8hjxJcj8bhHZ2eaaOwUnncKZtmwkLV6ORa4kgNqLftLDZR0+/esWSrXowthYyTDKxoOsc15hmT28KJ+tJYMi2daV7MrEmWPl2Vklm3oEc9ie6aRDSMhus6WiJ4cIXHDDVqotVC/kAY3wB98QyH5pZ0Mo7D2Ek52XUM6N/PsXIuOeMTiR8gNPcuO1TcTy8Q43Zrh6dwRSnXgZ1wzN6JRRVd3lobYaZQ6gWJ27S2uhDkT3MlhYyt7nQ6GnBrfl8sBpVg/7nL60BiuV/v3+0ysDWd5n/FxTGdpOsSdTLSzO9nKbkNxsDSKN8sGLsMTfrn3Vl617Veqas9shVo7SK5TMqbNkUt6WPfw0pWqAcJHnmD90SfJbL2Bkw3bKFTBw9m8UAbZ1HpCTZ3s6X+Y9oYu1qYuooUL2Zc4y8nU7KpVNfVBLiccOtgAbCIU2kh3d554oh84ilLTf3iZqkBv8QF6eYDrgPHAeo5bl7NPreFQMYq7SOUxARKmR5NZokkKJI0MnjJ4uNiFU+8lfBEONVq0bW9BDqUZS9fPzHeTOVKI8Xjb9Vwx/p0lya83NUBvaoBXAblAhKdbetkVDrHHSZGeYZiZZyjGA7WrNdNCXcd8c9UQvxcKIkvcPVuUIv70j9hiPcTYjldxUvpwanSPFrMxkOtJyWEe6f8mO1bdxI6hbnqam9ldOkx+EbybaRaXYlE4ciQKrCUQ6KNvbZpodC+ed+6ey0n7ENvsQ2wDbCPOqeAVHJIt7LNbGXNnP+wwbCiaDIcms0ijZEmSIqFGafAGafDOEnNOI47N5M4JF1vr+b71evYWF+ZTfykYDAjWpgSrh2xOHRtfUt/7c+GTIzu4NPyTJZ8fO2rnufzsAS6nPHT0SFMPuxua2GM4HC2N1tXZ0lXfdc4dh7rpe2T+M2tVAy+aZGj77Zwutta0w1k4lsHOPUZ7vIc+60I81+NA8zCHx2t7fjQLxzCgry9HIvEsrjc4rzRGAhdy1LqUZ71VjLmBcmnYyJMgTZJx4mqIBrefBvcMAW9hQ4cOh2/h285Vc/o4qCXdRUX+wDjZfH02G72rbQ/Xj99TazOeIxVqYE9zD7tDAZ6yx8h7JV6+5uW8ecubq5qPbqNeIULd6IT4va/bSLH2D1ipZwuHV72CfKF2VX8iHtH4YfLDB9mx+iai6ShjiRJ75CipGabo1CwXFKtW2TS3HMTzTtbamBmxjTiPht7Mg4XeZTFGPOwpus4sra/w2RI2XO6KfmxJx17PFleEg029uBtuZuvWN1Q17dkK9fL4HDyPGbOKnLi4q9ZmABA8tY9NT3yCjujSjW2ejFIG2dQGgo3XsuvsgxyRp0kWglyd3siW5FoM0bf08kY4cSLIrie3MtB/IyLroU4HswW8NNfm7+J3rC+xLlj/TTAFQzjSE6ZrawuhQH11yit4JveHb661GVNiKsXmkRNszdRunm79VlsG3LNmGBWoj+4ERjFP98OfYaOzB7OGz3oh24DiRsbE4JGBeylG86wfbOI66yJaYo21M0xTNfr7A+zetZ6TJ24CtRWhvsRlgib7Gd5c+BteH/4FMaP+y9bHYgZsa6ajNVprU17A54c3Uwi11tqMukQL9TJgOFDg1MXdtTbjBTQ89UO2Hv0q8Wjt3JopZZBLbSSY9EvXxjNEbYsrRtZyfXA7OxIbWZXoIhqq/dhwzfwZHTXZs6eXw4dvwnMvRiRYa5NejCi25L/Ou9Q/c2V4oE7rAJ4nbcKJvii9m5oxjfqQgZISvhesz1J1ramPK6Q5J99cO4Ky6qNUPYE1fJL1j32M3lB/Te0oZBtQxo2MIzwycC/5eJ5Y1qJ3KM72oS5uTF/Ay2QHlzVsYX1yFY3RJFL3r1LNZDIZ4emn29n/7PXYpcsxpL5KhAAhb5ib8//Cbwa/QW+g/jyEvQARDidNYjtaaE6Ea20NAP8xtIFspL4KJfVAfb35NdMyEMhz5uIeuh9f2nHV50Ich7ZHv0TDhss53HQ1pRr1eVOeQTa1kUiyk11nH6CYTdPS2E1TrJN4qJmwxGjPRukoRoE2HNMjFS8xGsgz4qYYyY3heHXg9FxzTgoFYd++JkzzGtatyxCN7cVbYC/uatNe/DlvZxdPR97A94oX1PXsYkMWmJvi9A2FOXm0tsO4lMC95k28kc/XzIZ6RAv1MuKedaO880mzKlO2VZvIwZ+xJX6Ik9t/hZFs7b7O89k4YtxEoiONa2YYdMY4nT1BIT2Ma5cIBiO0NPbSGOog5iRZbcdZV2xCuWvIxmzGInmGVZrhwjiFBY7RDpgBQoEgISuAJQYGCssIICqIcoO4xQDKtmhvhoKXZcxLM5pPac9rs8R1hQMH4ohczpo1BZKN+/G8atbuGBgSBgkBQaCE582+Q5GBw7b8l9hgdvGj4Jt5oli/fSdcgUNtAboSLRQPjpPJ1e4e/O+RNdzatIZk9ljNbKg3tFAvI/oDOfq3ddP5RH2OGzbTI6x++C4Sl7yaY2ptzcZcK88gn0kCSaCnbFsYwskigWCWgqQ5XRigNLqPQnoE5XnEYk20qB4SbhubzCZCXhclSzEWKTBqZBgupcgUsgQDQcJWkJAZJGwECUoAC8FUIMoF2wGniHIUjicU81ByLFyvgUIhgnJf3CHq2Kjigu4u1qebEQW5iEs6UmDcLDDmlsXb0b7Ep0Up4ejRCLCDnp4SrW2HUd4pxAgDQYQwiiBKBVFeAM//ua6J61o4jonjGNi2Qakk2LZBsQiO88JSsGEoLth6FsPYMyf7Iu4ZXuX+AztC1/Et7wYGnfp97Z4JCaGtjfSeKXLyVO1Gd/y3uok7+UzN8q839DjqZUZ3KcZvfi2D1Ml0dtNRD2OuZ4V4BMMFrEAGIYVrj1PMDVPMpkBBU7KTpngX8XALQQlT8vLk7TS5Uop0boRcMU0wmiAQbkbMJJ4bp1SI4jpznwGqJRlkU8jAyL1QlJVS5GMuqUiRMSPHmJNhLJ/C1VX1NWFNX55k8jGUmrtrTlfCPBF+E/cV19a9K9LVOcXYgVEKpdrcZx9t/jLNmQM1yXtKtr4Wdv5WVZPUvr5XKKeDWQYv6qZ9V307gwie2semoWOcfcmb6M8lam3O9CiDUj5KKR8F2sthAqGERyiSAzPNiDfOwOg+XCdPMNyEYTWijG6c0EZQQWxHsKvga2V4vMSjBmzrihEbLz7X3U1EiOYsojmLTmJAGwpFNuaSChcYN/KMOWnG8im8OpureiVy7GiEZPKlrF27G9eb2zzLpipwWf5uNltr+YH1KzxTx65Ij0eFhm1NdB7Pc3Zw6Wfj+pJ7I/8XdSTUNUQL9TLk3o1pfn2P8aL5UuuNiTHXiYtu4nBoG+4yKgAqz6CQbQAagOcdzuQnzUdf7TKR58GuU1m6W8L0oZDi1CdNEBqyFg3ZBrppANrwRJFtcEiFioxLllE7QyqfxlP1fZ8sR8bHDfbs2cHWrWdAnppz/LhzhNc5H2BH+Fa+WrqqbqfyzBhCZk2Edc0hzh4cw1nCmrwHxtt4fcuFdKSfXrI86xU9PGsZciKUYfCi5TOEYWLMdSKq21lny+nhAj9P2RSSoVnHMZQQTwfoGWpg62AH14yt5xX2Dl4auojtiY2sSXaTjMT10LQq4brCnj3dZDPXIjL3pg6AdYXv8I7AtwgbtW+CnBYRDidMAtubWbU6iWUunWx8rnRdXU2OUSu0UC9Tvr0xC8byeeFawydZ92jtx1wvJ4q2x89PZTkTC6Cs+T2qpick0kFWDcW5aLCTa8c3cot7MdeEL2J7YgOrk13EI/Vb/bocOHw4yonj12MY8/Oq1VF8jDvM/657r2bjlnCoIwgXt7BqXeOSuCF9PN3MqcTFi55PvaOFeplyJJxi+ILlU6oGENel7dEvsSXzMME6dC5Vrxzuz7Or6OHEq3PSTFdoTAVZNZRg22AX141v4hb3Yq6OXMhFyfX0JjppCNefM5F6ZnTU4OmnLgEumFf81tKT3GF8hXidizVAzoBDLQGK25vp3dRMLDK/2oTZcnfuped9qVoL9TLmO1vyIMunVD1B5ODP2LL3czTH6n8ig3ohm3d49EyW4UQItQg1KZZr0DQeYs1gkh1D3Vyf2sIr1MVcFbmQC5Pr6El0ELT019VMOI6wZ/cqctlr5lUV3mQ/zR3GF2k061+sAUoGHE6apC5M0r2lhcb47Jtp5sJTuQRHkzsXJe3lghbqZczB8DijF9THzFpzZWLMta4KnwvCvtNZ9iF40cXvBxqwDZrHQ/QNNnLxUA/XuRfQFEsuer7LnUOHYpw6eR2G0TLnuEl7P+/gszSby6fnpSvC0bjBwOY4HRe10tZcfd/6n8pcjSf1OSnLUqCFepnznS3FZVmqBhClaP35fxEJn+8VW3NjJFXikcEC6WRoSasEQ0WTK1Lr6E10LGGuy5PhYZNnnr4UYfOc48adI7yDT9JmLbPOlyKciAin1jfQsqOVzvZY1ZI+mI+xP3FV1dJbbmihXubsj4wxvnl5lqqh7Ct81fgTtTZj2aEU7D6V5XDQRIWWrqRhusL2wW42N/YtWZ7LFdsWdu9eQz531Zyn6Iw5p3i7dxdd1vJ0J3smKBxfEyVxSRu9PQmMKhQmPpnaiWcsbnt4vaKFegXwvQvqfJaecxDb+yCN0eX5Qqo1Z0eK/GzcJj+HYVwLRUTYMNDMpfHNGKJfIefi4ME4p09fj2E0zSlexD3LW91/Y1W9z8I1A0MWHO4OEbyklVVrFja062QxwtOJa6to3fJBP2UrgGeio6Q2L68e4JPpOfbDWpuwbLEdj1+cynIqOv9hXPOhazjG1eGthAK6k9m5GBqy2Lf3MkQ2zileyBviTe6/0hecu7vSeiJlwqH2IOqSZnrXNxIOzq+PxSfGXoJr1seUnEuJFuoVwvcvWN4l0uCpfXRE0rU2Y1lzdCDProKLXaVhXLMhOR7kGu8CEnos9jkpFoXdu9ZSyF8xp6rwoDvKr9r/xIZgfhGtWxryIhxuDpDf3kjv5mYaonOryh4ohXii4fpFsq5+0UK9QngqNkJ6Q2etzVgQ7Xu/haHvyAWRLbg8diaL07B0Yh3Jm1yV2UBnfH4OP843DhxIcvbs9RjG7HvQB7w0ry99mAtCVXAqXwfYvrez9NYk0fDcStefGNmBY1Wvo9pyQL8WVxD3Xbg8xl9OhzXWT491ptZmrACE/VmbpXQfbbkGlw6vYn3jqqXLdBkzMGDx7L6dGLJ+1nEsleeXCh9hW6h2009WG1uE5tVzm7Rn3A3wSOyGxTGoTtFCvYLY1TBMdv3yHjrT/OQ92mtZFRhN26QTS9fBDMoThWwZaGN7YoP2Jz4LCgVh9+51GMbsP24Miry68BEuDY8uomVLy4mEMedS9adHtlEK1vGsfFVGC/UK4/4La23BwjBKBVbln6m1GSuCvWdzSzp0a4JVQwmuiG7FMvXkfOdCKeHA/i0YRnzWcQSbW/MfYWd4eBEtWzrmU6rOuSYPRm5eJIvqDy3UK4zH40Pk+tprbcaCiD/1A+KR5eOZqV5xXMXJGjX6t4yFuNbYSiykfYafi1xOOHvm8jl1MBM8Xp77J64OrwzPficSBtHQ3D7sPjt0AYXQ3L2/LUdm/RSLSEREdovIh/z1sIj8i4j8iYh8WkQ2Vez7NhH5exH5gIi8czEM10zPTy5a3q72RCl6+n9SazNWBMcH85QStWlLiGUtri5sorVhbuOHz0f6+y3y+cvnFkkUN+b/lRsiJxfHqCXEFqF5zdxK1SUl3Bc6P0rVc/ncfh9Q6ULq94HjSqm/Af4R+BSAiPQCfwT8kVLqPcBvylwHD2oWxKOJQVRoeTf0Rg4/QWs0V2szVgR7R0soszZtxkHb4LKxPlYnl6/3vKXiwIEEsGXO8a7J3cXLIkerbs9ScyJhEJljqfqLQxvIRZZ3v5zZMCuhFpG3Az8BjlQE3wb8FEAptQfYISIJ4Bbg50qpCTfEPwVeWTWLNefEFUV6dXOtzVgwnQe+u1zdmNcVmbzDaKx2H26mJ2wb7GJrcl3NbFgu7H1mFYYx96arK3Kf5pWR/Ytg0dJhi9Ayx7ZqF+F/zJctkkX1wzmFWkS2Ahcopb42aVM7UOmhIuWHTRc+Od3fFpHHReTxwcHBORuumZmT3cu7RA0QGDxOd2io1masCPadyeJFatu5a+1gI5c3bME0lnfTzGLiOMLRI9sRmXuP/Utzn+e14acWwaql40Ry7qXqrw73kY6u7GGBsylRvw4oiMgfA9cCO0Xk94EBoLKrYsIPmy78BSil7lJKXaaUuqytrW2+9mumYXdLttYmVIXW3fcQOD/98FcVpeCIq5Z0tq2paB+JcnXgAsLBpR06tpwYHzcYHb0S5jHE7aL8l3l9+IllOzjOFqF1jqVqJfB1uWmRLKoPzinUSqm/Vkr9lVLqb4GHgMeUUh8GvgVcBSAi24BdSqkU8F3gJSLPVVpeBXx7UazXTMv+8BheQ/XnhV1qjFyaXvdwrc1YEZwdKVJYwsk7piORDnKNs4XG6PkzDnaunDgewnEumVfcLfn/5o2hn2LW/LNsfhyfR6n6W6O9jDWs3KaVufT6fj1wHXCliLwZ+AiwRkT+HPhD4DcAlFIngQ8B/ygifw98Uil1oOqWa2ZECYyvgHZqgOSu/yGq56yuCs8MFZZ04o7pCBdMrkivpzuxvIcSLib79rZiSN+84q4vfJu3hn5EUJbfczOfUjXAV7wbF8Ga+mDWny1Kqa8CX50U/LvT7Pt54PMLsEtTBY51mTStAN8h4rr0jv2c/eHLam3KsqdQdBlsCtGeqf3UiZYrbB/pIZvIM57TE7JMRinYv38jmzaP4nnjc46/qnA/7wjl+LxzGwVveVWGH0+Wx1Xni86s49w31skvNW+hLbNvES2rDbX/tNYsGk82zv3hrldi+35CY7T24rISOHA2i9NQHw3/pidcYq/F1LOxTEk+L5w+ddmcnKFU0lF8jF8zv0LcWF7zAMy3VP15+4bqG1MH6KdjBXMsnMFtXDnTD3Yfu6/WJqwQhIM5d0kn7ZiJWNbiwvjKbV9cKIODJtnsFfOO31x6ijuNz9FsLi9vf/Npq3403cKZxLZFsqh2aKFe4Yysaay1CVUjdGo/ndGVU0tQS4ZTJbJLPGnHTKwaTNCV0KM/puPQoQZQ83fkn7AP8Q4+Sac1+6rkWlMuVc/eB/oEny1ct0y70U2PFuoVzuEV5rSn/al7MfUw3KrwdH++JpN2TMdF4z162NYMPPNMN6Yxfw9vMecUb3M/yupAsYpWLS7HE+acS9VPZho5mLx6kSyqDVqoVzhPrKB2agAzNUSPsfx9G9cDjuNxyqyfV0DQNrjY2lBrM+oW1xUOHboQQ+Y/0UnIG+JNzj+xIZivomWLh20ILfMoVX9o5FqKwZXjY75+nlLNotAfyGG3r5zqb4CmXd8iFFpplVu14dhA7SbtmIqWsRAbkqtrbUbdkk4bDA3tZD7OUCYIeGle//+zd99Rkl33Yee/973KsXMOk/NgZoBBGJIAI8QkUxJtaaVdWVbknt09Z732ynu8Xtm7XuvIXouyJCrYokUFiqYYJOYAEARBAuIgzAyAyal7emZ6OlZ3VXXl8Kru/jEzFDCY1JXuq3r3cw4OTld3vfr1dNX7vXvfvb9f6ffY422PlfazEROfZ32j6rWKm8+5f6JJEbWeTtQOsDK2/itSOzNKBcZzp1WH0THOr5XBsMnKMmDLaq8uhnIXc3MeyqWH6jqGS+b5B4Xf5aAv3qComqds1LYC/NuJUS5Fa1+EZyc6UTvA1GB7bc24H6FT3yMcaK9VrHaVypZJhu0zqjargv2lDbom+F2cO9eNITbXdQwDi/fnfp93+BYbFFXzzEaNdY+qAT6eeCclT7QJEbWWTtQO8GokQae1oRJSMjb/guowOsaZefVNO94omHOxJ1RfIupsgnPnNmEYdd6HFZJ35v+Y9/lm7v2zCpUNQX8No+q45eaLnvafAteJ2gGSriLF4c4oJ/pGvsvH6dc9qxtCSrhis4mXsZWQLjF6F8Wi4NrsgwhRf/GaR/N/zkd8Z2zdzGM2auLzrH+W5evxcS5HH25CRK2jE7VDLI0HVYfQFEPnv43Q7+KGmF8t2KJpxxvtWRvB5/GpDsO2VldN0qnHGnKsvfnP8Y98R22bFEoGNY2qAX47+S7K7vZd92DXv4nWYOf7y6pDaArX6jVG3G/poqrV6LRNmnbc5C4bHHDpKfC7mZnxI6uNqca1Lf81fs77PC6bNvOYjbpqGlWvlj18yfuRJkTUGvb5RGpN9VoojrTRntlG6jvxdd2zukEKxQorfnv9Y/YkvWztmlQdhq2dOTOMaYw25FgbCt/lF9xP47Nhsi4Z0D9e28j4y/FJrkbrWy2vSmeeubW3yJsW+bE+1WE0hZHPMG7pTqqNcmEhQyVor2S9JdZDV6D9V+82S7UKFy/uxBCNucU1XDzMP3F9maANm3nMdtU2qgb4+Nq7Kbvbb7uqTtQOMj/Wuff6IsefIuiz30mlPQmmCkDHNT4AACAASURBVPba+mZIwYHSpN6ydRfZrMHS8iM06rTeV3qdXzL+mi7TXp+reu5VL5e8fLUNp8B1onaQM30F1SE0jahWGYu/ojqMjrGyViJjs4VlgZyLvXrL1l0tLrgpFhu3wjlaPs8/4c/pt1kzj1rvVQP8TXwD1yL7GxxRc+lE7SAnAwmk115Tmo0UuPAyPcH2aThgd2eW8sgaT4bNMroSYjTSYZ1mGuzC+SiGaFzN9JB1hX9c/RNG3fZZkFrPqBrgt9feR9nVPjthdKJ2EMuokpnozPvUNw1PP1NPGWTtDcpWlQW3/U4Ru9eG8estW3d14cLGht2vBvBXlvgp+XlMGzWQvFbHveqlspdv+NpnCtx+n0Ktqa4Nd+6IGsCzOM2wL6k6jI4xs5SnbKPyoqC3bN2PfF4Qjze2yEe0fIF3+mcbesx6FEV9o+rPxzexEGnMtrZm04naYU71dn4lr/7T3+i0iqlKnU+XkTZq2gHQnfSyvWuD6jBsbXbW07D91Tc9kv8s3aZ9Fhpe63Lhddd+e+Z30k9itcEUuE7UDnPWn6Aa6OxpQzO1Sq8/qzqMjrGWKZOy2agaYFOsm+6g3rJ1N+fODWEYvQ07nilzfND1YsOOV6+igIE6RtXXin6+5f/xBkbUHDpRO4wUkJrsvLrft+pbOak6hI5yZsFeTTvg+pat/cUNuEx7xWUnliWYn9uPoHGLAjcWvsNOb6Zhx6tXvaPqz65uYSm8u4ERNZ5O1A50ZcheK3mbwXfxFbxe+yx8aXfVKlyqSBstJboukDN5ILhJdRi2FouZlEoPNvSYT1p/a5uFZUUD+ifqK2Ly8ez7qbj8DYqo8XSidqDjPfa5Gm4WISUD0v59dtvJUrxou73VAMMrIcYiQ6rDsLXz57sxGlRiFCBsTfNu39WGHa9e813uukbVswU/TwfsOwWuE7UDzfhSVKIh1WE0Xdf0YdUhdJxTC1mqAfvtHNiVHCbgte+ISDUpYebSToRo3IXWQ4XP0uuyx8KyQh01wG/69Mo2lsO7GhRRY+lE7VCJiS7VITSda/UaXYGS6jA6SrUKF4oVpL0WgeO2BAeE3rJ1N6mUQSbduC1bLpnnA+bfNex49Zrvru9eNcDvZN9PxbTfYludqB1qZthmZ9om6U+dVx1Cx1ldK5EM228KvCvlYXt0g+owbO3SpQBCbG3Y8TYUnmW3TRaWFYz6VoADXCkEeDb44QZF1Dg6UTvUsS5nFAUJnv8hLr0ouOHOzGexQvabAt+00kNvsPNni+px4fwGDKNxHaTea33BNv2r57pMPK76RtV/HtvBSnhHgyJqDJ2oHWrJncPq6/w9qKJcpN8dVx1GRzqXtpCmvWZmDAn7CpN43fYb8dtFoSBYiTWuL3PYusx7vDMNO149CoZgcLK+UbUU8J9yH6Bi2uc9pBO1g8XqnCZqFz1XdVetZljLllnx229U7c+bPFHayUhkQHUotjU356FafaBhxztQ+Dx9NllY1ohR9aV8kOeCH2pQRPXTidrBpgft1We2WTxz5wn77XES6TQXFnO2qwUO4CkbHFgZ40Bkmy6Icgfnzg5iGI1p0uOSeT5oPt+QY9WrYAgG69xXDfCp2C5WQ9saEFH9dKJ2sGORBE4pit1fsMfUXCc6nSgiXfY8lYyshHic3fSGulWHYjuVimDu2r6GVS2bKDzHHm+qIceq13yPC3edo2op4PfyH6RqqJ81suenS2uJpKtIcbjzy4kChM8/j6Hf7U2RLVRYsFnf6jcK5E0ejW9gV3QTwiEXpvdrZcWkWGzc/er3Wl/EY4OFZXkhGBqvf1R9MR/iB2H1q8D1qcvhlsfs3zmmEYxcmj6fPbaRdKKZ5TxFG1Ytu0kg2Bjr4nHPHsL+zi/2sx7nz0cxjPGGHCtkXeE93ksNOVa9FnrcuMz6U9wnl3eTCKndo68TtcOd7y+rDqFlepZeVx1CRzsZKyBtPLIGCKfdvD2zlc1djUlMnUFwaXpHw6qWHch/jgGX1ZBj1SNnwHCd1crg+hT47xc+TFmoW+ugE7XDvRqJIxtw1dkOfJdexacbdTRNsVRh1mbbtW7HrAh2LPfzWHAXPo/9qlCpkE4L0qnGVC0zKPIh4/sNOVa9lnobM6o+lwvzHflYAyKqjTPO0Nod5Q2Lwljj+tXamZCSgeq86jA62mysQM7GU+Bv1Jvw8URxB6ORQdWh2MLMTADB9oYca7T4PA941xpyrHpkDBgea0xxl9WKulryOlFrLIw6p5lBdMo+tYk71cmlHNLXHlui3GWD/SujPBjerrdxAefPT2AYjamv8B7rc7ZYWLbU68Zs85Wk7R291hBn+4qqQ2gZV2KRnmBBdRgdzbIk0xVs0q34/gyvBnmC3fSFnLEL4k6KRUFs+SGg/lsYQWuO9/ou1h9UnTKmaNioWhWdqDVeD8aRbueMJnrjZ1WH0PGWEgVb9q6+G3/e5JHVSXZHN2MI554a5+fdVCuNqVp2IPd5Bm2wsCzW58E07L9+4k6c+27UfsQyqmQnG1OhqB0ELx7Grb6GQcc7OW/P3tV3I4RgQyzK4+49RPztPQqrx7lzAxhG/SVYBWU+ZD7bgIjqkzZheLR9/546UWsAXBu2XxnIZhGWxYC5ojqMjielPXtX349QxsXb0lvY0jWhOhQlKhXBtdm9DalaNlL4IQe86rv1rfZ5MNq04I1O1BoAp/pyqkNoqa7LL6kOwRGu965uz4tAsyrYvtzHocBu/A7cxrW6alIoHmzIsd5lfR6f4oVlay7RtqNqnag1AM74E8hAe91TrIdncZpIQP29Myc4M5+zZe/q+9WT9PJ4cQeDYefcHrrpwvkIhlH/rELAmuO93vMNiKg+yX5vW5aR1YlaA65X30lNOGM/9U19WXuUOnQCO/auXg932WB3bhSjzbf5rJ9gemo7hqh/RmFf/osMu9RWQky4YHSk/UbVTnvXaXdxZdg5K78BQheex7B3xcuOYdfe1evhz5tsDo+pDqPlMhlBcq3+KXBBmQ8a321ARPVJDngQDdh+1ko6UWs/cqLHWU0rzHyWfpu05XMCu/auXo+NyR7crva+4KjFlcsBBDvqPs5w8UUe8sUbEFHt4i7B8HB7NWbRiVr7kWnfGtWIM7pp3dSz8JrqEBzFzr2r74e7bLA96MyV4NPT4whR/0XKO0ufw2eoXViWHvS11ai6fT8xWlMkJrtVh9BSvpnXCfjaqYZWe7N77+r7MbYaIeB1Ttndm7JZQam4r+7j+CuL/JhHbdGhVTcMD7XPoEQnau1NZgbb5yqzUfrLs6pDcBS7966+F7Mq2OFx5qj64sXuhtQC353/G0bdaheWZYfaZ8udTtTam7zWrb7jTatFL75AG+7YaGvt0Lv6boZWAnQFGtO8op1UKoLU2t66j2Ng8UHxdAMiql3MLRgeao971TpRa28y78li9TrrBGSmVujx60YdrdQuvavvRAjBDsZVh6HEzEwA0xiu+ziDxVd42LfagIhql2+TUbVO1NpbrE5EVYfQcr3xU6pDcJx26l19O71JL4NhZ9UeuE6wuFj/CnCAx0ufx62wYtmyWzA0YP971TpRa28xPeC8xVWBiy/hcd6uG+WOL2SxQu27ZWt7aUR1CEosLroRYmvdx/FXFnnEu9SAiGpXHA4off37cc9ELYQwhBDfFEL8GyHEbwoh/loI4RdC9AghPimE+JdCiE8JIQbf8Jx/IYT4d0KIPxRCfKS5v4LWaMe64jjtpq2oVBgwllWH4TjVKrweL1L1t2exnXDazUS0/mngdnR5ZrIhTTsOlr+pdMS45IHBfnuPqu/33+dFKeX/K6X8DSAAfBT4LeC7Usr/AHwF+DiAEOJR4N1Syn8N/DPgd4QQXY0PXWuWuKtIadBZ27QAumZ+qDoERyqWKpzKWm27uGxresCBpUUhlTKoNKBvdci6woOKi6BYI/bebnfPd5eUsiql/E0AIYQLGAPOAx8GXrzxYz+88TXAj998XEpZBs4CTzQ2bK3ZlsfbYzVkI7mXrxINqN0y4lTpnMWFimzLeuC+gjNLiwJMTfVhiPqnjh+x1K4AX/AIBnrtOwV+35eBQoj3A98AviGlPAoMAOkb304B3TcS+Rsfv/m9t3QgF0J8TAhxVAhxNBaL1Rq/1iQX+p3ZWaovc1F1CI61slbiqttsy/7VG5M9eBxYWrRYFORy9RdB6S6fZbdXbQnj6kgHJGop5dNSyg8AG4UQ/zOwDNxsQxIBElJK65bHb37vLTf/pJSflFIelFIe7O/vr/kX0JrjtUgcHDidFzr3AmZ7zsB2hGsrBZaD7be4zF022ObQ0qJTUyFMo/4WoIfk9xoQTe3mffYdVd/PYrJdQogPv+GhGWAT8E3g0I3H3n7ja7g+6j5047kuYBfwfKMC1lojY5YpjDpv64lRKtDvSaoOw9GmFnOsRdpv25ZTS4tKKVhZ2V33cQaLR9nsyTcgotpJm46q72fIVAR+RQjxG0KIfwvs5PrCsX8FPCmE+A2uLy77dQAp5cvAc0KI3wL+APjnUkp95mtDC2P2fNM2W/fcUdUhON6p+Sz5Nttj7eTSoteueTHEhrqP83bx4r1/qInmfIK+bvtdbN1zT4SUcprrifh2fu0Oz/nteoLS7OFsX4GNqoNQwHf1NMGR95AtOG/q305em8/y8FAAd7qkOpT7NrQSoKs7QjLnvPaps7ObGR27AtReh2G88H3GPO/gWlnd7Q9jNAgJtSP7W+kzkXZHx0NxpLs997fWq798RXUIjiclvBYrUAm0zyKt66VFnbkCPB43kbL+KfB3GMcaEE3trvkFvV32Ki2qE7V2RyWjSm7cefepASLndaMOOyhbVU6mSkhv+6zw6036GAzXv7iqHV2aHkaI+m5ZbCo8TZ+r0qCIauMas9f2VJ2otbuaG22v+4SNYmYS9PqzqsPQuN7D+mypinS1z+lqR9GZpUVzOUGxWF8RFEGVx12nGxRRbWZ90BO1z6i6fd75mhKne+11r6aV+lZOqg5BuyGRLnPJEEijPaY5QhmXY0uLTl3swjDqa+yzvfANIma1QRHVQAjcY/YpK6oTtXZXp/wJpN+Zo2rfxVfwep3XoMSuFuNF5n2uOpYqtZZTS4tWKoK1ZH2jalMWeIdbbfGhWb+g2ybbBJ33LtLWpWpI0hPOvE8tpGRALqoOQ3uDy8t5EpH2KIhyvbSoM3tWX77swzDqm/7fU/wafkPhZZkQ+GxSSlknau2erg47c+U3QNf0YdUhaLc4O58j0yZ7rDcmux1ZWhQEiwv19ax2V9O8zXO1QfHU5opf0BVS/17TiVq7p+M96Xv/UIdyrV6jK9A++3id4vhchqJNpiXvxsmlRZeWXMC2uo6xv/Q13ELtqDpgg1G1TtTaPU35U1TDzqxSBtCfOq86BO0tBK8t5bBC9h+tOrW0KMDlmQmuV5Kuja8S41HvUgMjWr8rQUE0pPZ2i07U2n1JTjqvP/VNwfM/xOXc2X/bqlQkr8dLVP32/uM4ubRoOm1gletbWPZQ+ZtKE5UUguBY+N4/2EQ6UWv3ZWbIuW8VUS4y4Fbb2F67vWKpwulcBem29/tzaCVAVyCiOgwlpqZ6MUTtW51C1hUe9Kn9/F0NCbw+dReE9n53a7ZxvMt5tYvfqPvqEdUhaHeQypa5KEGa9t1jLYRgp0NLi5ZKgky2vp7Vj1pPofKvWxWCYq+6NRE6UWv3Zdabweqrr4hBO/PMnSPkV1vWULuzWLLErM3r0vc4urRoCNPor/n5XeVz7PGqXdRqKcyWOlFr921qp3MTNUBPeV51CNpdzK7kWQ7be4+1U0uLSgmxWH0NOw5Vv9egaNqPTtTafXtqJIb02H+VbbNErr2uOgTtHi4u5EjZeNuWk0uLzs15MMSmmp/fXzrGFo8zSxrrRK3dtzVXicU9Q6rDUMa9eAm/r10KWDrXyfksyajXtqVGnVpaFODq1Y3Uk3bejjMLEDnz3aLV7NmNWZzc/7FXxlSHoN2H03NZZv0uW3bc8hVMNkecWVo0kTCR1dqnwMeKP2DM7bwCRPZ7F2u2Nu1bI7N5UHUYyoQXdEetdjEbK3CqLKkE7He7ZmPCqaVFYXp6qK6e1Y8bRxsYTXvQiVpbt5e2O3dE7Z09jcfe65W0N0hlyxxdLZC3WW1wJ5cWzecFhULt27U2Fr5Dv8tqYET2pxO1tm6Ho8uU+7tUh6GEkJJeM6E6DG0drIrk1bkssbAHaaNrTCeXFp26GMUwaqt2KKjyhOtUgyOyN52otXWTAs7udWaVJYDIyjnVIWg1uLCQY9plIj2m6lCA66VFdzq0tGi1Kkgm9tb8/G35bxI1qw2MyN50otZq8tTgEjJgr+nEVvHPvKprf7eppUSR13MWluImCzcNrQYdWwTlyhUfhlFbtTaDIu9wX2hwRPalE7VWk7xhMbvXmYvKhGXR48moDkOrUa5Q4ZUl+/S03pMdxWU688pvfq72Npi7i18nYNh1E15j6USt1ezpiSQYNrrp10JdiYuqQ9DqICUcn8uyEHQrfw/7CiZ7ghuVxqBKLOZCsL2m57qrad7mudrgiOxJJ2qtZvOeLMntzqyy5L90BIfWrOgol5bynENQVdgZCWAkFmIg1Ks0BlVmZsYR1LZuYH/xq3hE54+q9alGq8sLW521TeImo5in21dQHYbWAKupEsfWSpQi6u5bCyHYkx/DZdhjoVsrpdMGllXbwjJvdYVHvAsNjsh+dKLW6vJqeJXiiDNHAl3ZGdUhaA1SKlc5orj0qD9vsivkzCnw6el+DBGo6bkHy9/AtG3B2MbQiVqr24k9tX3A2l1w+ghKm+RqDSY4PZflqk9d6dGxWJj+UI+S11apWBTk8g/U9NygdY0HffEGR2QvOlFrdftO7yLVsPOStZlJ0OUvqw5Da7BrK+pKj16fAh/HdOAU+PRUBMOo7SLlUeupjr5m1olaq5tlVLn0gDP3gnbnZ1WHoDWBytKjgbzJrrDzpsCrVUjEa2vYES2fZ4831eCI7EMnaq0hnhpdRbqcNwoIXXVegwCn+PvSo96Wlx4dXw7TF6qtxGY7u3rVX3MRlEPV5xocjX3oRK01xKq7wMou523Vcq0uEPZXVIehNdGFhWzLS48KIdhbmHDkFPjCfG1FUPpLx9jqyTc4GnvQiVprmO9vduZ2pW5rUXUIWpMtJYpcavFrBnImO8MbWvyq6i0vu4DakvXb+LvGBmMTOlFrDXMmkCA3OaA6jJYLX3tddQhaCyzGixRafM96YjlCb9B5nequXJ6oqQjKWPEFJtzFJkSklk7UWkMd29X6lbKqeRam8Ps6ex+ndt2ZlUJLt24JIdhbnMBwWBm8VMrAqtRWBOXtRuetG3HWX19ruue6F6n0OK8FZo+MqQ5Ba4F8scKqv7XlRoM5lyOnwKenaiuCsin/HQZdnVUxUSdqraGkgPN7nTdVF110ViN7Jzu/kKMaaG2ynoxF6Q5GW/qaqhWLglyuhlG1kLzPPNz4gBTSiVpruKeGY0ivs6bAPVdP4XHWr+xol8q0tGilQPBAaRJDOOuUPT0dxTDWv01tQ+G7HbUC3Fl/da0l0maJxd1DqsNoKSElva6k6jC0FllKFFq+sCyUdbEjsqGlr6latQrJxJ6anvs++fWOqVamE7XWFM9szIDolI/J/YmsnFUdgtZCrV5YBjC50kVXwFlT4Feu+DGN0XU/r6d0iod9K02IqPV0otaaYsaXIr1lUHUYLeWfeRWX2rbGWgsVihVW/K2932FIeKA84bgp8IWF7TU97x2lL3REv2pn/bW1lnppu7NG1MKy6PFkVIehtdCFhUzLm3eEs262RSZb+pqqLS25EGL9RVD8lUXe5W11qZrG04laa5rD0WXKA85aAR5NTqsOQWspwaVSteXdkDeudBENhFv8qmrVWgTlQOELdJnVJkTUOjpRa011eo+zTiaBS6/gsNoUjrecLLa8y5YhBfsqGxAOWgeytmZQqax/YZlL5vkx17EmRNQ6+pSiNdV3BpaRgda3ClTFKOTo8jmz5rmTnYm1fmFZOO1mW9RZU+DT0wMYwrfu523Nf4NJT6kJEbWGTtRaU+VNi6t7nbWorDt7WXUIWosVSxViLa5YBrAp1k3E75xZq0JBkC/sW/8TheRJnml8QC2iE7XWdE9PJHDSfHDw0hE6ZgOndt8uLmSpBFu9ClywrzqJcNAbbupiBMNY/9qXweLL7POtNSGi5nPO2VNTZsGTI7HDOb2qzXScqL+sOgyt5QTTxUrLF5ZF0h62dk20+FXVqVYFyWRtDTveWf4SZsv/QvXTiVpriee3OitxdReuqQ5BUyCWLLV8YRnAppUewv5Qy19XlSuXfRjGyLqfF7ZmeNw/14SImksnaq0lXg+tUhjrUx1Gy4SvtPcqU612Z2IFpLu1p1azKtgnN7T0NdUSLC3uqOmZjxS+QMhor+1aOlFrLfP6zvWv1mxXrtU5Qv6K6jA0BYqlCsve1i8si6Y8bI06Zwp8cdGFYMu6n+euJnmv50wTImoenai1lnm2b4lqJKg6jJbpsRZVh6ApMrWYxQq1vp3a5ngvIZ9zPmNXrmyoqQjKrvyXGGqjntU6UWstYxlVLu110PT33OuqQ9CUEUznWj+jYlYE+8XGlr+uKmtrBpXq7nU/z8DiSfOFJkTUHDpRay311OgK0iGdKzzzU/i87bfCVGuMlVSJrIKFZdE1D1u7nFMIZXpqECHW/+88UXiO7d5sEyJqvHsmaiHEZiHEXwsh/oUQ4veFEP/mxuM9QohPCiH+pRDiU0KIwTc8518IIf6dEOIPhRAfaeYvoLWXVXeBFQf1qu4VndFmT6vNmeV8yxeWAWyJ9TimHWahICjUUgQFeG/la22xA/1+3kE9wOeklL8tpfynwM8KIR4Cfgv4rpTyPwBfAT4OIIR4FHi3lPJfA/8M+B0hhLM6M2h39ezmvOoQWiayeFp1CJpCpXKVJQULywwpOFCaxDTWf/+2HU1PRTGM9V+YdJfP8qhvuQkRNdY9E7WU8oiU8qu3PCcLfBh48cZjP7zxNcCP33xcSlkGzgJPNCpgrf2d9yfJbXRGWVHvlRN4Wr+mSLOR6cUcVsjT8tcN5FzsDW1u+euqUKkI1pIP1PTct5W+iM/mPavXNScjhPgp4Gkp5TlgAEjf+FYK6BZCuG55/Ob3Bm5zrI8JIY4KIY7GYrGagtfa1ys7nHGlL6Skx5VUHYam2FTOQiqYYx1dCTEaccZF8eXLPgxj/RUQ/ZUl3u2dakJEjXPfiVoI8W7g3VyfzgZYBm5Wg48ACSmldcvjN7/3lrkFKeUnpZQHpZQH+/v7a4lda2PPdy9R6YmoDqMlovHzqkPQFFtNlchG1HSR2702jN/jhBoGgqWl2oqg7Ct8kR7TvnUP7itRCyE+DLwf+KfAkBDiEPBN4NCNH3n7ja8BvnHz8Rsj7F3A8w2MWesAUsC5B5yxdME/fRTTGRMI2l2cWcojPa1/I7jLBgdczpgCX1xwI8T6i6CYssCTrleaEFFj3M+q74eAzwOPAc8BXwW2A/8KeFII8RvAR4FfB5BSvgw8J4T4LeAPgH8updRzf9pbPDW0jPS2/t5dqwnLoqdNtoFozVO2qiwqWAEO0J30sr1rg5LXbrWrV2orgrIl/xQbPMXGB9QA91yOKKU8Btyp2vuv3eE5v11PUJozZMwy83tHGT16VXUoTde1NkXMXdsWEq1zXFrK0z8cwJUutfy1N8W6We5KkMi2Z6vH+5VMGoyN7UIYJ9f3RCH5MfkUn+QnmhNYHXTBE02pr29KOKIAiv/SEYT+tGnAhUxZycIyQwr2FzfgMjv/83bp0hBCrH+7RX/pGA/6Ek2IqD761KEpteTOMb9//e3q2o2Zz9LtL6gOQ7OBRLpMRtHCskDO5IHgJiWv3Uq5nKBcqq1n9ePlL+Gy2XYtnag15b6yKY50wGbjrswV1SFoNnFmKY/0qllhOLwSYizS+dUBp6Z6MURg3c8LWVd4wjvbhIhqpxO1ptyKO8/sgfXvf2w3oUv2XVWqtZZlVZk31Z1+dyWHCXj9yl6/FcplQS5fWxGUg8XPE7ZRz2qdqDVb+PKGlY5fAW6m40QD7dNaT2uuy8t5ymE173m3JTggOn/L1vRUuKbSou5qmic961yM1kQ6UWu2kHQVufxQ50/HdRftNaWmqXU+VUaaatpCdKU8bI9uUPLarVKtClJrtd2r3pH/MiPucoMjqo1O1JptfHkihgyoWWTTKuHLr6oOQbORtWyZOQVNO27atNJDb7CzCw/NzPgxjPWXURVUeVJ8v/EB1UAnas020maJqQc7e1TtWr1G0G+fe1+aeleW86QV9K0GMCTsK0x2+JYtwepKbaVFx4ovsNObaXA866cTtWYrXxlbpBrs7LrEPZUl1SFoNnNiLoul6H61P2/yQKCz71dfu+bFMCZqeu57K19VnihVv76mvUnOtLjwUGd3+wnPva46BM2GjseL6rZsrQYZj3b2zouF+fXXAAeIls9zyLfY4GjWRydqzXa+NrJINbz+/Y/twjt3AZ/XXgUVNPUKxQpTFZRULQPYlRgi6O3cz93ysgshttb03EPFL+AT6rpr6USt2U7etDjzUJ/qMJqqV6yqDkGzoeVkkZWgmilwlyXYLzYhUHSl0AJXr0xQS9rzVld4GHV1EHSi1mzp68MLVLru1Aum/UWWzqgOQbOpC4s58ooWl3WlPOzo4C5byaSJlLtqeq5PqmtmohO1Zkslo8rJB7tVh9E03suv4+78qqlajU4s5qgE1LxBNi530Rvq3M/eTI0NO1TSiVqzrW8OLlLpiagOoymElPS4OrvdoFY7qyI5k7WQrtafogWCffmJjt2ylc0aWOXaiqCoohO1ZluWUeW1B9df/q9ddK2eVx2CZmOpbJlZt4GKZYf+vMl+f22rpNvB9HRtDTtU0Ylas7Vv9y9g9XVmsvZfOoqpEBOFUwAAIABJREFUZjeO1iZmYwVSilpiDsYDTHTolq1iUZAvtM+oWidqzdaqhuTog2HVYTSFsMr0eHOqw9Bs7tR8hlJEzUrwnfHBjt2yNT0Vqalhhwo6UWu2952+BUqDnbm4pW/hKEJ/CrW7EpxYKVL1tX76xVUxOCA2IUTnbdmqVASp1B7VYdwXfYrQbE8KePnBzryq9828xrbsETrwPKg1ULFU4WJZIo3Wv1GiKQ87Ihta/rqtcHkmiGn0qw7jnnSi1trCc92LFEd6VYfRFIHzh9laOKaTtXZXK2sllhVu2eoL9Sh57WaSElZXd6oO4550otbaghTww/1q7tO1QvDs37Gl+LpO1tpdTS3myCkohiKE4EB6gpAv2PLXbrbZWR+GMaY6jLvSiVprGy90L1MYt/80Va1CZ37A5vIJOriCo9YAr89nqQRbP7L2lA0eKW/B5+m87nZLi9tUh3BXOlFrbeWFfZ1ZhOGm8Knn2GKdVh2GZmNSwqlUGelu/enbnzd5RG7F7Wqvyl73srjowhD23TeuE7XWVg5Hl8lNDqgOo6nCJ7/L5qquBa7dWSZvcdlQc/oOZ9084t6Goej1m+Xq1UnsOp3VWf/SmiM8t8+eH6ZGipx4hs1SVy7T7mx+tUBC0f7qrjUvDwW2K3ntZkkkTKixYUez6USttZ2j4RWymwZVh9F0keNPsYmLqsPQbOzMfJaiomQ9EPezL1Jbf2e7mpkZQQj73V7TiVprS888oKICcutFX/8WG8W06jA02xIcXy5Q9atJLmMrYXZENyp57WbIZAQVy36lRXWi1trS8eAq6a2dWYf4Vl2vfYMNxozqMDSbKltVzherSFPNLaHNsW42RkeVvHYzTE/3YQh7rWzXiVprW0/tKeOUjcfdr36NDa4rqsPQbCqeKrHgUzdluzM2wEikM25HFQqCQuEB1WG8iU7UWts6E0iwtt0Zo2qA7qNfYcI9qzoMzaZmlvJkFBRDges9rB+Ij3RM9bKpqSiGEVEdxo/oRK21tW/tKjpmVA3Qe+RLTLjnVIeh2dSJ+SxWSM3iMrMqeDA1SdTf/t3uKhVBJm2fhh06UWtt7YI/SXzXiOowWqr3yN8w7llQHYZmQ1LCqWQR6VHT6NxtCR4ubCLg9St5/Ua6dCmIYdijv4BO1Frb+8aOHCjoKqRS3ytfYMy7pDoMzYayhQpXDIGqfRHeosmjla14XO1dm19KQSK+W3UYgE7UWgeY8aWI7emcVaf3q//lzzHmi6kOQ7OhuZUCaUX3qwECORePurZjGmpG9o1y9aoPw1A/Y6cTtdYRvr4tjTSd93buf+mzjPpWVYeh2dApRc07boqk3Dzs345o8zUkS0vqK7A578ymdaRZb4blvc4bVQMMvPQZRvxx1WFoNiMlnE6XkS51p/nehI8DIXt3prqXxQU3htikNAadqLWO8bWta0hXe0+11Wrgpc8w7E+qDkOzmXTOYl7RwrKbhleD7IluVhpDvWZn1VZf04la6xjzniwL+505qhZSMvjSpxkKrKkORbOZy8t5cgrvVwNMxqJsjU4ojaEe8bhJNqsufp2otY7y1U1xpNt+RfVbQUjJ0It/yWAgrToUzWZOLuaU1QO/aetyL+PR9i1QlFpTt+VMJ2qtoyy781zbr36VpipCSoZf/HN6g3nVoWg2YlXk9XrgCrcxCiHYszLEYLhPWQztSidqreN8adMK1VD7F1yolZCSsSOfJuyvqA5Fs5F4qsRKQN0qcABDCg4kx+kORpXG0W50otY6TtJV5Nl3dTmqtOitjFKBjWc+j9frjHag2v25sJijGFF7v9qsCA5mNhLyBZXG0U50otY60uHoMlcfGVcdhlLmWowts9/CdOZCeO0OTq4UkF61bwpP2eCR8hZ8HrUXDe1CJ2qtY/3VpgUKY86+H+aZn2JL6kUnTy5otyiWKkxX1b8h/HmTR+Q2vO72LjXaCjpRax3LMqp89rEy0uvsE0Hg4itsrF5QHYZmI0uJAknFU+AA4aybt7EDv8enOhRb04la62iz3gwvvqtfdRjKRY9/m1HvsuowNBs5PZ/BCqu/iA1kXbzN2q7vWd+FTtRax3umb5HlfWOqw1Cu/5XP0R/MqQ5Dsw3BqUQR6VafBnwFk0P5rXQFIqpDsSX1fyFNa4G/2BmjPNClOgylhJSMHPkrwgG9bUu7LluoMGuaylpivpGnbPBoZjN9oR7VodiOTtSaI+RNi799h4l0ObNq2U1GqcDGU3+NT2/b0m6YXcmTVVxi9CaXJTi4NslQWN+ueiOdqDXHOO9PcvLx9i1h2ChmapUtV76Bw69ZtDc4MZ+lorgYyk1mRXAgPsZ4RH9Wb+rIRN1fBY/QZyHtrb48Ms/aDueWGL3JvXiJLYkf6m1bGnC9JebZnIU07fGGMKRgb2yITVG9tgQ6NFH3WSV+RugSddrt/cW+JJWukOowlPNPH2VT9ZzqMDSbWMuUWfLbY1QN12uD74wNsL1rg+pQlOvIRA3wnrmz7PXq+xzaWyVdRb79RBAUNiiwi8jxpxnzLqkOQ7OJ6cUceZvcr75py3JP2/ezrtc9E7UQYkgI8adCiCNveMwnhPhDIcT/KYT4MyHEtjd87+eFEL8jhPiPQoj/sVmB349fXrhM2NQb6bW3OhZeYeqQs0uM3tT3yufpD+htW9p1J5byylti3moyFuVAZNu9f7BD3c+I+h3AV4E3Dj/+N+CqlPLfA78LfApACDEG/Drw61LK/wP4VSHE1saGfP+ixSy/WLLPVI5mL5+dnCO3cVB1GMoJKRk98mmiAUt1KJoNWFaVi6Uq0mYTTiMrIR4O7cQQHTsRfEf3/I2llH8D3NqJ/sPAize+fxLYJ4SIAO8Hjkkpb+79eBH4YOPCXb8Dy9M87hlQGYJmU1LApx/OUQ3oWRdRLjJ5Um/b0q5bWSuxGrLXFDjAQNzPo/4duAxndZqp9dJkgDcn79SNx+70+FsIIT4mhDgqhDgai8VqDOP+/PfXzjPgDjf1NbT2tOTO8fy7elWHYQtmOs6Wy1/X27Y0AM4vZClF1JcYvVVP0sdjnp14XM6ZLa01US8Db8x8kRuP3enxt5BSflJKeVBKebC/v7mLvryVMr+WLmBgs7kczRZ+0L3I3EF9vxrAvTTD1sQLetuWBsDJ1SLSY7/RazTl4ZCx0zFtMmtN1N8EDgEIIfYCx6WUKeBp4CEhfvQxPwR8u+4oG2BzYo4Pu/UqcO32/mLrIsURPbIG8E2/yqbKGdVhaDZQKFa4jLBFidFbhTIuDlV2EPQGVIfSdPez6vudwD8GhoUQvyGE8AO/D0wKIX4D+N+BXwGQUl4DPg78rhDid4A/lVJebFr06/SR2dNs9HSrDkOzIcuo8vlDVaTXOdNpdxM58QzjngXVYWg2MB8vkLLZlq2bAnmTQ6WtRPydfWvznnejpJQ/AH5wm2/9L3f4+c8An6kzrqYwpeTXVlf4fyJeSlKvcNXebMaX4ugTIzz8zKzqUGyh75UvUHzbr7Cc08VhnO7UXJZHhwK4MiXVobyFt2jyWHUzR0OXiWeTqsNpCsetcx/KrPJz6FZq2u19a2Ce1b26bOFNI6/obVvadcdieXI2HVm7ywaPpDYyEO7M21eOS9QA75w/x35dtUy7gz/bHcPq1RdzAMIqM3n8v+H32fEupdZKVkXy2lyWawE30mW/1GFWBA8mJhiNdF5tBPv9a7fILy5cIaKrlmm3kTMtvvKEB2k69uPxJmY2yeZLX8Ht4Nv3HjdMumaJBsqqQ1HuynKeE8UqVsh+W7fMqmDfyghbujprF4djz0SRYoZfKtlv24FmD6cDCc6+Q0+B3+Revsqu03/BBmOGgMNG1z3BIjvOf4aeo19i0+E/Zs+1LzHuWcDr4OIwmbzFy4s51qJe260IFwi2L/fzcGgnLrMzigI4NlED7Fue4V2ezpsm0Rrjb0bnSG/VPXFvMnJrdL/6Nba/9Al2pP+O/kCuo/dbCwEbzMtMHP4TzNTqjx53r8zS98oX2PnKH7Ajc5iBQAbDoWfSU3NZZjwm0mu/Qc9A3M8T7KIr0P6dFB369vp7Pzt7lkFXZy/t12ojBfzlgRTVSFB1KLbjnz7G2OH/yt7pzzDhnu240qN+n2TnyjN0H/sqQt7+dxNS4p86wujhT7H37KfYJC8QceDCu4V4kWNpi6INq5j58y4eS21iY5v3tXZ8ovZULX4tk8fQ/xTabay6Czz9zjAdPXSsg5lapffIl9jxyh+wPfcyvYGC6pDqNhhIs+31P8U7e/9FX4x8hujxb7P58B+xZ/HrjHqX8dgvbzVNsVTh6HyOWNiLtFn7WLMq2BUb4GBoR9tOhevsBGxKzPMRV2cu69fq90okxuVH2/uKvNmElAQuvMTE4T9h79XPM+5ZwNNmi89ME7ZYpxk5/GcYhdrbfroXLzHw8l+z6+gfsD3/Mn2BrGOu8y4sZDmPsF2bTIDBeIDHxS6igfabQdWJ+oYfv3aazZ4e1WFoNvWZTQskdo2qDqMtuOKL1+/hvvqHbC2+RlfAfkUybhX2V9h59cuET323YccU1SqB8y8xfvhP2XvhL9loXCLsrzTs+Ha1mipxJF605Z7rQM7FofQWJqMjqkNZF/td9ihiSPhYbIn/uztAoaq3YGhvVhGSTxxY5OCWQd77agXftRXVIdmeUakQOvs8IZ6nPDBBYtM7WLL6sWx2G3fUu0z/kS8imhiYmU3S9erX6QJKI1tITjzGcqWXcoeeam7uuZ4c8DNaqiCsquqQfsSsCPbEhujpDXMiO0Wlav+LJ52o36A/l+DnogP8OQnVoWg2dTS8wrEn4MmVUR45ksJM3NqqXbsd9/JVBpY/S7/bS2b748Qi21nLqT39eNywMfkigddfae3rzk8xMD9Fv8tFbushlrv3kMx15g3tK8t5Vv0udkc9tis/OrIaJBLczaveS6TzGdXh3JWe+r7F4wvnedB72xbamgZcXw3+nf5F/uMHCpx9YgLpt98Un12JcpHwqe+y6fAfsXv5m4z440oWXd3cGx242Nok/UbCsgiefYGNh/8zu5e/yaB/rSO3edl5z3Uo6+Ltma2MR+29DVOPqG/jF+cvcWlggGSl9gUlWucrGVW+MD5H17CXfzg9zuhrc4iKfab47M4zP8Xg/BSDQGlsO+mh3ax5hps60hYCJo3LdB3+2h23XangmZ9iZH6KwVA3azvfw4IYo2SvAWjdTs1lGe7xslGAKNpnutmsCB6IDdPbF+JkZppK1X6fYZ2obyNUyvHLBfhdN7a7AtTsJ+kq8qnt84xvCPNTZ0J0n5lTHVLb8Vw7T++18/QClWAX+Y0PshbZSKIcath9XL9PsnHuu+vadtVqZiZBz5G/pdvlIrPjCZYiu0jn7FdMpFYL8SJxj8nePi/elL2uREZXwkRDezhmTJMpZFWH8yY6Ud/BnpXLvGdyL8+WllSHorWJWW+GTxzIsG/rAO9/TeK/GlMdUlsys0lCp75HCBgRgtLEHtKDu0ia/aTztSWtwUCaoVc/V9e2q1YSlkX41PcI8z2Kk3uJjT5GLB/oiJHDzT3X24aD9GVLiKp9fqlQxsXbza2c7l7gWso+536dqO/ip2fPcmZsAwvllOpQtDZyPLTK8cfhPfFRDh3J4FpZUx1S2xJS4r1yEu+Vk/QBlWg/2Q0PshaaIFEIULnHDKppwsbiacKHG7ftqtW8V04yduUkQz1DxLe+m6XKgO1WztfiwkKW1YiHrUEXZtY+y99dFYN9K6P09IU5lb5EVaqfCteJ+i48VYuPrWX4zYBBBfV/LK29fK9nkeefNPiJhQl2HVnGyLZ/1S7VzLUYkeNPEwHGXC4Kk/tI928nQS+5wptXYoX9FSanvoY7dlVNsA3mii8y8PJf0+fxkdr1HpZ8m9/yO7eb1VSJ1RTsHAnQkymDjUbX4ysRouFdvMolskW1MzE6Ud/D5NoiPxnZzd9aehpTWz/LqPK3o3N8Z8jDP5qZYPzYfFP36zqJsCz808fwTx9jALB6x8hM7GfNP0qgmqbvyBc68t/aKBXoev1bRIWgsPURlvsOEM+1986Ds/M5IkE3OyIe3Gn73LuOpD283b2NU9F5pXEIaYOVjwcPHpRHjx5t3AEXjsPT/1fDDieR/H+Tu7hQWr33D2vaXYyUgnz0bITe03Ngg8+e1hnKQ5tY3fg4S8UubLhoeV02D/kZLNirSApA9cEIgwc3NPSYQohjUsqD9/q59p43aRGB4FdjC7rLlla3eU+WP9y3wBd/spfcRt1iVWsM9+Ilhl78S/ae+wsmzau426zO+htNL+Z5NV+hYLMSpMGyuqI0eur7PvXlkvz7XJLFYA8nuwY54RacLyWwpH32A2rt40wgwZm3wbt2jPLE91cQ+aLqkLQOYOTW6Dn2ZaLhHub2/jSrOZ/qkGpSKFY4NpdlvN/HeFXaat+1CjpRr9NQNs5QNs6TQNF0c7Z3nOP+ACeqGRJWe2z90Ozj+z2LXPlQhJ973o87llQdjtYhzHScicN/QnTfB7ns2kYblLO+rdlYgQWXwe5BP8G1Ig5pQvYWOlHXwVsps3/5EvtvfD0bGeBEtJ8TRoXpUoJqJ2x61JpuxpfiE+9187Fjw4QvLqgOR+sg0ePfZlffKa5u+wgpxbXVa2VZVY7PZRno9rLZJTDynbdA8F7a8y9nU+OpZcZTy3wYyLr9nO4d44TPy0krRbqit+Zod5Yxy/zuw8v8Qu8EG17qjO1Emj24V2bZFP/PxB/6KLPWaNuuYVxOFIkJ2DUSJJq2V6GUZtOJukmC5TyPLF7kEa6vGp/pGuV4pIcTosTVUlKPtbW3kAL+cvMcT0ZHOfS9JUTZeSMHrTlEtUrvkb8hNLGLmZH3kS+05ySylHB6LktX2M32kP06cjWLTtQtIBBsSs6zKTnPTwFrvhAnukc46XFz2lojX3XGm027P8/0LTL349189LkCZtLe7fe09uK9eoZti5dYfuhnWMh3qw6nZsl0mZfTJbYNBenLlxGVzh766EStQLSQ4fGFCzwOWMJgqmeME8EIxynocqUacH1V+NKP+fjllwcIXFlWHY7WQYxSgaEXP01026Nc6nqsjbt0CS4s5pjzm+zq9uFJde7OCZ2oFXPJKjtWr7JjFX4GWAl0c6J7iOMuwflykpLU059Oteou8LtvK/GrPeMMvjarOhytw/gvvMyO4Hnm9/80K9mA6nBqls1XOJLPsmHAz4hVRZTadIn7XehEbTN9uQTvySV4D1A2XJztHedEIMiJao4VS0+DOo1lVPkvu+b5qe4J9v7gmu53rTWUmU0y/sP/SvSBJ7ns3nXPJid2dnk5z4LbYNeAn8BaZ42udaK2MXfV4oHYDA/c+Ho+3MeJ6AAnXJKLxYRuFOIgXx6e49qHB/jAs0nd3ENruMiJZ9jVe4ar23+StTbdxgVQLFd5bS5Ld9jNaMRDpFhBFNp/VrJ9/yIONJJeYSS9wgeAvMvL6d5xTvj9nLRSrFXyqsPTmuxIOMb8h0L8wgsBPItx1eFoHca1OsfGF/+YxEM/xdXKeNtu4wJIpMsk0tdbZ/Z3eRkJugjmrbadFteJuk35rSIHl6Y4yPXtX1ejwxyP9HLCqDBTiuvtXx1qzpPh997l4tdOjNJ9Zk51OFqHEVLSc/RLhMa2c3nsx8i2eRtNgFiySCxZBCQjvX4GfSb+bNl2TT/uRifqDiAQTK4tMrm2yEeAjCfAYrCbtNtLyuUhZZqkDIOUkKRkhZQsk66WyFYKOqG3obxp8YkDi/wP3ZNsOXxVd+HSGs5z7Txbly6z/NBPM1/oVR1OgwjmVwvMA0LAeJ+ffo/Al7ZXH+zb0Ym6A4VKObaU7l13vCog7QmS8gZJefzXk7rLTcowSBuCFFVSVYuULJGuFCjrBiS28t82XOOd0RHe+WwMUWzbPTaaTYlykcGXPkNky8PM9LyNTnqLSQlXY3muAi6XYKLXR69p4E4XETbM2TpRO5ghIVrMEi1m7+vnM54Ay4EuFn1BljxelgxYkmWWrAyFarnJ0Wq384PuReZ+PMp/930L16reg681nn/qCDsCF1jc/1GW85GOm8CxLMmlpTyXAK/HZKLXS48EM1OyTRMQnai1+xYq5QiVcmy6zffWvEGWgj0seQMsuz0sGlWWqiWWrazeC95kU741/uh9Xn716BDB6UXV4WgdyMitMXL4zxnoHiKx7V0sVgaxOvBjXSxVuLhwfTYy6DMZ7/HRValiZtUORHSi1hri5sh82y2PSyRJf5TFQBfL3gBLbheLQrJULRKzsrqfd4MkXUX+0yMr/FL3OGNHdXEUrTlciUX6X/4cvR4f6Z3vZsm/pSMWnN1OtlDh3Pz12cZo0M02QxBSFItO1FpTCQTd+RTd+RQ7b/meRLIYHuAHPUO8YCV0zfM6VQ3Jp7bP86HucR56cQUjo7fsac1hlApEj3+bKJDb+gixgQPEsz7VYTXNWrZMPF9hVNHr60StKSMQDKdj/Gw6xk+aHv5uaDPfNUssl9OqQ2tr3xqY59sfgYcyg+yf9zA0ldDNPbSmCVx8hcmLrzAyuIHVTY+zVOqhqifKGkonas0WfJUS75s7y3uRHO/fxDMBH2dLq6rDaltSwNHwCke3A9thT7aPhxYDjE2v4YqtqQ5P60DupcsMLV1mIBBmbdd7WTQnKBTtshyrvelErdmKQLA/NsN+4FpkgO/2DPJiaUVvDavTqWCCU5sTsBm2FHp4ZDHExEwW77y+GNIay8il6T76FboMg+z2d7DcvYe1nFt1WG1NJ2rNtsZSy/xiapl/6Any/cENPCezJCv33h+u3d2Ub42pDWuwAcaLUR6NRdk4kycwu6KLp2gNI6pVQmefJ8TzFMd2sjJxiFg+rN9iNdCJWrO9cCnLP5g9zQeFwdHBLTzjFcyUEqrD6giz3gyzYxkYg75ykLevdLPlSong5Zju1KU1jPfaWUavnWUo2k9i+7tZlMOUdemF+6YTtdY2XLLKY4sXeAyY6h7jmWgXx4orVHUXsYZYcef56nAehiF60Mvb4r1sn60QmY4hyh24aVZrOXMtRt8rX6DX7SW9650sBraTzXfm9q5G0olaa0tbEtfYkrjGaiDKs33jvFBZI1vtrB60Kq25Snx7YIFvD4B/v4tDyUG2LhkEchaebBl3roSRySFKOoFr6yfKRSLHv0OE71Ae3Ehm7AGS3hHW8h49NX4bOlFrba03t8bPXF3jJw0XPxzawnddFgtlXUqzkfKmxfd6F/nebXoz+Cte+iwf3WUPXWU30ZJJqCAIFiT+QhVvtow7V8aVLVzvo63Pwtot3EszdC/N0A1U/EEKGx4k1bWZeCVKSZdWAHSi1jqEp2rx7vlzvAvJ6b6NvBoMc1HmmS+ndIewJsqbFrNmhlnvvX9WSIMey0dP2Uu35aGraBIumUSzEMpW8KeKuFM5zHRefUIXgmrQR6krSCHsIRNyUXJDf6xE6FoCkdezN81g5rMEz75AkBcYEoLyyHbSI3tIugZJ5Z2brpz7m2sdSSDYs3KZPSvXv866/Ux3DXHRH+KisJgpJ/VWL0WkgFV3gVV34a4/56q6GC4HGCz56Cu46c4ZRDKSYNbCmyrgTmbr7hYmvW6saJBi2Ec27CYdFCQCkpi3xKKvwJI7R8koAbe8zkYQD8OWfA+71oKML0u65lOYcT2L02hCSjxz5+idO0cvUAl2kdv0EKnwBuKlUEfWGr8Tnai1jhYs53kgNsMDN762hMGVrmEuBqNcdBlMWSnSlbsnDq21LKN6fTW6NwPh2/9MyPIxUg4wUPTRmzfpygnCmQr+dBlPKo+QklLETz7iIRMwSQYlq/4Ky94ii548SVcRSN/4b32kgIuBNS4G1mAY2AeD5TAPrEWZXBX0zWXxLiVs3+O43ZjZJOGTzxIGRgyD4vge0kO7SBp9ZPKm6vCaSidqzVFcssrmxBybE3N84MZji6FeLob7uOj1cLGSY8nSJUztLuMqc8G1xgX/GnTd6adaV+t8yZ3jmb4c9AHbIVDx8ECmmy0JD0MLRQJzcURR70dqFFGt4rtyAt+VE/QDVtcg2ckDpILjJIoBKh02aaYTteZ4Q5lVhjKrPH7j65Q3xFTXIBd9fi5icaWUpKK3gGnrkDMtXorGeCkKbACjKthR6GNnIsDoskXk2hpm6v76wGv35kouEU0+RRQYc7koje6gFBmi6O+h4IpQkD5yJbNtE7hO1Jp2i0gxw4NLGR688XXJcDHTPcxlf5gV0yAhYFWWiFcKetpcuy9VQ3ImkOBMIAGjwIHrVeF2pcIES42vh+2pCCI5STBTwbdWwJ3KInLOWAAnLAvvlVN4OfWWOyeVSC/l3glKkX6Kvh4KZpi89JEvGlRtfC2uE7Wm3YOnarF9dZbtt/le2XCxGogS9wZZ9fiIu9ysGoKEqLJaKRKv5ClJB6160e7brDfDbH/rupr5q15GS0EGCl768i668oJwtkogXcazlsdMZRFWmw4575OZWsVMrXJrQ04pBJWuQco9o5RCAxT93RSMMIWqh1zRUL4JQSdqTauDu2r9aOr8TtKeAHF/hLg3wKrbS9w0WTUgLi1WKwXWKjm9hUxrurxhXa/z7uO29/WFhF4rxHDJT3/BQ0/eJJqVhLIVfOkSnmS2Y3ucCylxJRZxJRbx3/I9aRhUukcIbnkXMKYguiYmaiHE+4CPAsuAlFL+22a9lqbZWbiUI1zKMXmH71eEIOGPsuoPE/f4WHV5iBuCVarEZYnVSp5CVS9E0ppLiutlZFfceQje/mdCFR8TxRCjOS8DGZPuVJVgsohnJYXRoXvLRbWKa/UanvSyshiakqiFEAHgvwC7pZRFIcTfCiHeK6V8thmvd6spOcpnXP9rw49rCImPCl6zgocKXqOK17DwUMEjKniwcIsKHmHhpnL9P2HhkhYubvwnLVxUcMkyprQwsdQXd1BICBCyglm1MKQ1nF/2AAASsUlEQVSFKcsY1ev/CWlhVDt/2tiUkr5ckr5c8o4/k3d5/36K3e0l7nITNySr0iJeLZKw8nrBm9Z0GbN8414711e4v0GXFWCyGGIk56U/I4iuVQgmCnhW03Xve3e6Zo2oDwFXpJQ3L7F+CHwYaEmiLkg353J32ICptRUhwWtW8QoLnyHxmRX8RgWvuHGhJCy8oopHWHiN6xdQHqOCSYfeayte/y/I9f/GbzxcxSBuuoibJnHToCQqIKoI48b/sUBUkKKCoEJVWEAFSQWJRZUKVWkhsajIm19XqMgyFWlhST2i1+4u6SqSdBU5HgT63/y93nKQDYUQwzkPvRlB15pFIJ7HHU/rhi/3oVmJeoA3VxJI3XjsR4QQHwM+duPLjBDifINj6ANWHHrMZh3X6bHq31///vr3b7z2iPWvPg0///ONPu6d7oi9SbMS9TJvrikUufHYj0gpPwl8skmvjxDiqJTyoBOP2azjOj1W/fvr31///s79/Zt53HtpViPQF4FJIcTNUv1vB77ZpNfSNE3TtI7VlBG1lDInhPifgE8IIWLAiVYtJNM0TdO0TtK07VlSymeAZ5p1/PvQjGn1djlms47r9Fj1798c7RKr/v2bw+mx3pOQDt4apGmapml216x71JqmaZqm/f/tnXm0XVV9xz/fvLyXMGQEgoQxBlqUsmSKZQYpIGUQqUALEQmgC4JiwoIYKEMghkGFtg6ggCjCoktYXTigEhQUlDRQhoYWFsUCMtQoarEUSMGQ/PrHb9/kvOu9991z7tnv3fPu/q111r1nuJ/7G/beZ59z9vntEiSdqJMkSZIkSZIulnSiTpIkSZIkSbpY0okakNQXgVn63HWSNimbGbgxdJ0ZgxtDYvg1xT/Fv2xm4Ka2qnxm18e/50/Ukq4ATpVU2gh4SVPNzCSV5l9Ji4EPS5pYFjNwpwVdS2sAJF0AHEsmG12nBVfSduGz1DIbw6+RfJriT+/GP3BTW1WBehVDz54+UUs6Cfg5sBTYqAzHSroM+ImkmWa2towKIGkOruetwIaSJpao6zOSdjKzNSUxTwaeAb4AbCBpa0kDoeAWaqwlXQI8J2nvsnwauHMo2a+RfFq6noGb4l+B+AduaqsqUK9ixb9n56OWtCkw3sxuCAHbFZgg6X7gVjPLnSk+9HR/A9wF3CjpNDN7VtIYMys0tZE8u9tYM7spNIK74rPJPi/pcjPrZFqax4FrgB9IOtzMnpTUZ2adzGjRZ2a3Sfow8B7CVZWkM8ys6GS2P8E7lfdKOsTMHujEp0GfWH4t1acp/kAPxz/omtqq6tSrGHWqp6+o+4DDJM0HXgDOx3tXBwIz88LC1YKAF/EpPh8Bvi5ph9BbLXrrbyPgGEkLgV8A5+KVaxs8NWtukctYfOKUC4CbgaWSdg69wIGC3InAkZIW4bOnLQC+BKwFjivAGxN6+WvN7OKg672S9gs+rZ/jPY+U6tdYPi1bz5i6pvhHiT+ktqrr61Xk+IOZ9dwCDITPM4C7gYMy+24CDuuAPTZ8bglcBfwQOBTYIydnHLBB+P4h4FHguMz+z2TXC+ran/n+aeBZ4Ci8oPbl4EwDJobvBwDPA2dm9s8HTulAz3GZ7+eGyjAbeD9+pdE1fi3Rpyn+PRz/DCO1VeWW1UrFv7b01BW1pHnywQPfkbQ9fkvtv4G5knaT1A+sBF7KwTxS0paZTWsBzOyXwKXAy8DXgLZTwEk6G7gEWC5pX2BF0HWBpP3DlcT/4c8C2xZJJ0maldm07naMmV0U/uObwFvW5q0aSfPwxnOZpOPx3uk/ABdLOkLSNGBj4Ikcep4l6ejMptXhygozuwq4AbgFeMXM3szBLd2vkXya4t/D8Q/c1FZVoF7Fiv8fSSe9nCotwGnAKcAAsBjv9e8FbA+ch/cmrwR2y8GcjT/nOQeYntleS806GbgQ2D8H80TgtPB9PvAz4HhgO+B04L6gZ95e7+HAU8ASYPcGum6Mzw++Xw7mB4C54ftHgNtqvsBvdS4FrgBm5WDuDTwAXAscmdUzLOOBvwL2zWl/6X6N5NMU/x6Of/hdaqsqUK9ixb/hf3UKqMqCPzfIVvxP4b3RbcL6FsC0nMydgbOAe0IFml63f0Ngs5zMc4CzMuunAg8Cu4b1KcDGBez/U+Bs/Grkc9mCFfaPBybXF7YhmHOBqzLrRwF3AO/P2N+fU88ZwLzQaNwIHFW3fyywYR49Y/k1kk9T/Hs4/uG41FZVoF7Fin/D/yr6w6osrO/dzAcuB6Zk9i0Bri7qQGDr8Lk33iM7D5iA96TyNlA1PT8AfB7YObNvIXA7HTzjYP1zmXcB3wA+C/xJ0HegIPPPgK8Ch2e2nY4PyijEDIz+0BgtxhvrA4GJZJ5VdoNfy/Rpin9vx79O19RWleTXKsW/1TLqn1Fb8CTwHeBg4Ozw3AzgTuBXmWPyyn+F//hn/NnHgXiF+gQwqaCe/4I3Uh+RtHvY9o/ACuvgGYeFV2PM7Cm8wE7Er1ouAYpm5nkJf252hKQPhm3fxG0onODCzFab2a/wkZP/ifeGrwE2L8CK5tcyfZriP0jXnot/na6praL761WkOtVQemKaS4V3AyW9G/gy8BD+msNk4F4ze7Ck/5mDXwWcYGbLCvxeZmaSZgCLgFV4Q7ga+JGZLS9Dz/BfRwddP2FmP+uAswV+FfVO4A3gFeB7Zekq6YCg58Vmdn9BxrD4tVOfpvg35PdM/AOja9uqmh+z38vwaZbbZH8l6lVZdaohezSeqBsFPlMBtgJ2wwe8PGhmK4oy6/dJOghY1W5lGkLPTYBt8dsqK8zsyXaYQ+maOWYvfCTiY+1ym/1PGC05CdgdeNrMco3wHOI/dgHeNrM8o4ZL92tMn9Y1gB3Hvx2d8+raxKcdxb9Nn+aOfxNOaX5t8R8d16nA6aitGoJdqK0aQs9oPg3/0zX1qsw6let/R9uJWp6u8A+Z9T/qBZbJ7EDP8cAaM1sd1tdlBOqE34rbob6lcIaBOR5Y3eh2Vgfxb8osKuFKdI2Z/abBvk7i35RbVCRNMrNXy4xXDGbg7gI8WSv/dfuKxr8psxORdGzgPtVgX1FdmzKLiqTrgUfN7LoG+zopq025RUXSO/AEOaXVq1bM4ZJRlUJUngpuP0krgYfN7M7Qe5QFCce1HbChmJnj8jDnAHsCqyQ9bmbfCL29MWa2tr4XmMP+ltyCup5qZl9rxKk7bkSZ4fi5wH7ALyTdbmaPZ/cX8etQzCK6SjoTeB/wlqSvmNkDWUYH8W/JLajrYjwr1gfNbGUznUaaGY6/Br9KXNCIUzD+LZkd6HoqfmW3om57fRuQq161YhbRVZ67egtgU3nmrbVZVgdltSW3oK6nA4cAb0q6xsIt7Q7j35JZRM8iMmoGk0n6OP4C/03AW8CFko6DQQMKsrd++iVtO0LMDfARgsuAhZIWBOagwhNOZP2S3tWm/UNy63RtyZV0DPBVSd/N6NOwzATmgKQ9pOYpCNtlZvQckhmOPwF/7nQdsCk++rKhtOvXdpk5fToXeBUfdPI7PGY1vQZNXJEz/m1x8+gaZA3wv8AtkqYEncbXH5QnVu0wC8T/auBNM1sgaZakgyTtU9OtTtd2498WM69PQ7l6zcwWATtKOkZ+JVzTrVGshmpXYjA/C0wFTsbL0/RmJ7icZbUtbs56dQ6eqGUhng1sskLazqL1ql1mgTqVW0bFiVrSJGAnM7slXEXcgWfZmSPpPZnj1lV+PCFD00kCYjCDrAGWm9lzwLfw1IAnSvpQlhk+B/DpAn/fhhva4mZ0bYf7BJ5LeIak78PgSt9A12MYemRqW8yMnkMy5QOOjjez280HHP0IOCLs2zxzXNt+zcNs16eh3OxtZrea2dP4oJbjJX1Z0ieDLyyPnnm5OXSttQ3P4a9g3Y9nyfoMnnt6nf0ZXVvGKg8zZ/zfi79jfE44Oe2Pv9O9WNLsJroOZX/bzJx1inDMQ5L+Er8C3gpYIs/l3ShW7bQrpTJDu3Gwmc01s1fwbF0fldTXov63U1bb5uYoqwN4GtRlZvYs3gn8GPAtSedn7W9X1zzMAvHPL1biu14juQDfBu7IrH8czzRzYFivPY8fhxfSrUaIeRHwSGa9H5gDzC/KLJubOTb7zuGTwF3h+wCDk06MCLOOPxvYDBD+Gs/lYfsCBudHzhOrGMy/DsxpeCKLPfGcw99lcHKEvPbH4u6Dvyq0HfBTYDk+wGnHLmOeCPwd8DdhfTKe3asWsyJ1tVRm5vgz8cxYJ2f2vQ/vvIzNw43BrIvTOLwTtRmwoMlxReJfKhef/OUhPGf5F4Edg/13Mvh99BFlFl2iQIdrCZX70PD9nfhV7z3AZcAOeIq3bMEdi6eN23qYmRPq1u8CHsisH4rnR65Vpr4Q+KbMWNx6Zmb7GOAx4GE8c9SUzPZhZw7BnYSntNwCz7X75yXYXyoTP/nXJlyYhc+JO6GT+JfBzRxbKzN74Y9TPgkchufYfpGQhSlP/MtkNin/h5BpLPEr4BtYP/lE7liVwWzCvRX4JWFSEWCPwB0X1ou0K6Uz6/Z9CfhY3bbCZbVTbgP79wU+SkhZi0+zejPrJ4wZEWYZSzRw7AVPX3ghnhf4Rvx2Cvg0ZVvhVxYLGNxLnwpMHWbmpfjJcsvMtgHg++F/TsATD+yS2b8RMGkI+0vn1jNZ37DWGqWZwP8Af5H5zVhapN6LwRyCqxCnn+IdrMMyv9m4oP2lM8P3d+P5m+eRyYddJP5lcJuUqXH4XaS9wvrfEu4oFYl/Gcxm3My+9wb7z2VwDubc9nfKbOGDfvxxyoN41qxLCOksw/4i7UqpzEz5HxM+d8Jv//Z3Yn8Z3GaxCuXq5/j80heSyYc+Esyylko+o5YP6HiHmS3BR+T+DjhJ0j5m9iLe+N8E/NjM/qP2OzN7xfy5yHAxN8Fv7xlwhqTp4Td/MLMj8LlgXwW+bZl3JM3sDTN7tYX9pXMbMc3WPYN5Wz7R+gR8MoR7a897zOxtM3t9uJhtcA2/Tb07sMjMlmbsf72g/aUzwyH7An8P3GdmD2eYuePfKbdZmcI7Kdeb2fLwHO46M7svw8wV/06Zrbh19l8J3GNmj3ZifyfMVlzz7GuHAF/HOybfM7N/zXCLtCulMjPlvzbQ6zXgfsu8ptZJWS3KbVGuMLPz8BSpx+EJYh7L7BtWZplSyfeo5SPrrgY+ZWZPhAb/Sry3eHI4ZnvLkXgjEnM8PhhmDT537q+Ba82nlSssMbjtMCX1Wb6p+kpn5uDuYWaPVIC5rZm90C4zFrcJ8ytm1vY0isPBbMGtt3/LPPUhBrNdbl6pCnMkdZU0zszeGklmmVK5E7WkfjNbLelzwG+BfzIf6YykpcA885Gv3cLsM7M18teSDsfn6/0x/ipFkWxTpXOrwmyTu8rM/i1zfDvZr0acGcv+kpiVjf9IMdvkvm45M66NELNKbdUbZvbvI80sWypzopa/JzwNH8yzBH+vdQE+cvgH4fNq4FIz+20XMKfjUwA+ndl3MD7V3BTgzDwVKga3Kswq6Zrs7237q6Rrsj+O/TGkEs+o5ckcVuGj7VYCj+PvtV2GP+9aFJabc5xQYzNfAh6WtGvmkBX4s+OLchb80rlVYVZJ12R/b9tfJV2T/XHsjyYWebRaGQs+0i47evEC/BlCbY7VzambCL1LmOfjt9JnhvUJhMnfR5pbFWaVdE3297b9VdI12R/H/lhLV19RS9pOUh+eaODY2nYzuwy4Hh+Fh5m9bGYru5B5BXAtcHRYf818BHlbEoNbFWaVdE3297b9VdI12R/H/tjStZNySDoDzwLze/z2xG2SxprZwnDIo/grU93OfCwvMxa3Kswq6Zrs7237q6Rrsj+O/cMhXXmilnQK7szZwN14hp1ZwDJJq/FBXjPwl/tHFbNKuib7k/1lM5Ou1WFWSddY9g+XdN2tb0k7AAfgE0y8jWes2cbMfo3n3n0Zn3Hlh5ZJ5jAamFXSNdmf7C+bmXStDrNKusayfzilG6+on8cz69Qy6KzG07SBz2byjJndNUqZVdI1BrNKusZgVknXGMyka3WYVdI1BnN4xbpgRFv9AvRlvk/FZ4HaAR8yv+doZlZJ12R/sr+X7a+Srsn+OPYP19L1CU8kTcBn1xkLfNHM7u4VZixuVZixuFVhxuJWhRmL2+u6Jvvj2B9VRrqn0EZPaAb+ftuhvcaskq7J/mR/L9tfJV2T/XHsj7lU4Yp6DJ6E5AVp6BzLo4kZi1sVZixuVZixuFVhxuL2uq7J/jj2x5SuP1EnSZIkSZIkvSxd93pWkiRJkiRJkmS9pBN1kiRJkiRJ0sWSTtRJkiRJkiRJF0s6USdJkiRJkiRdLOlEnSRJkiRJknSxpBN1kiRJkiRJ0sWSTtRJkiRJkiRJF8v/A9Om1A1qeD9XAAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 576x432 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "### Example 5b\n",
- "\n",
- "fig = plt.figure(figsize=(8,6))\n",
- "plt.suptitle('Stacked area')\n",
- "ax1=fig.gca()\n",
- "ax1.set_title('Cores per Socket evolution on HPC systems')\n",
- "plt.xticks(rotation=45)\n",
- "# random colors\n",
- "#colors=[]\n",
- "#for x in range(1,len(seasons)):\n",
- "# color = \"#%06x\" % random.randint(0, 0xFFFFFF)\n",
- "# colors.append(color)\n",
- "\n",
- "plt.stackplot(seasons,hpc_core_data,labels=ucores,\n",
- "# colors=colors,\n",
- " alpha=0.75)\n",
- "\n",
- "#ax1.legend(loc='right', shadow=True, fontsize='medium', bbox_to_anchor=(1.3,0.5), ncol=2)\n",
- "\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Decorations"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 56,
- "metadata": {},
- "outputs": [],
- "source": [
- "## Example 6a\n",
- "\n",
- "## Stacked area plot B\n",
- "import pickle\n",
- "import numpy as np\n",
- "import matplotlib.pyplot as plt\n",
- "import random\n",
- "\n",
- "## Read filie to obtain data and labels\n",
- "file = open('data/top500.pickle','rb')\n",
- "hpc_core_data = pickle.load(file).T\n",
- "hpc_core = pickle.load(file)\n",
- "ucores = pickle.load(file) \n",
- "seasons = pickle.load(file)\n",
- "file.close()\n",
- "\n",
- "\n",
- "### ... continues\n",
- "\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 65,
- "metadata": {
- "scrolled": true,
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAgUAAAExCAYAAADsn9ErAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsvXmUJVWV6P3bEXfOec6szJoHioJiqIGxEHBAFAQFFdtWLIf2Lft9732I0I02X7ftA0RBhSet4oy2jXaLCFLLBmSUsaCgKIqah6zKrMysnMc7RsT5/riRkJWVw83MO+TNOr+1Yt0bJ86wY95xzj57i1IKjUaj0Wg0GiPXAmg0Go1Go5kdaKVAo9FoNBoNoJUCjUaj0Wg0Llop0Gg0Go1GA2ilQKPRaDQajYtWCjQajUaj0QBaKUgbInKhiDwuIk+LyF/d/58REV+uZcs0InKRu89Pi8izIvKwiLxvhnX+QER6RWRjmsTMKCLyzyLSJiJfn0EdnxSRn6ZRrLQjIp8WkV0iEhORJ0akf9vd/6Micpeb9oSIREVkt3ttvCkivxORihHlKkXkXhF5XkSeEZGXROQWEVmYi/3TaE50RPspmDkicilwL/AepdQ+N+0DwMPAeqXU1lzKl0lEpBg4CFyklHrTTfsXoEop9f/MsO6ngV8qpX45xXJfBxYppTbOpP2pIiK/BBqVUl9PIe8i4KBSSkakmUBQKTWYIRHTgquo3aKUahiV/kvAo5T61Ii0RjfvT0XECzwOHFFK/a2IFAKbgXuUUj9w81cD/w08q5S6Lgv7sVEpdVEm29Fo8gndUzBDRMQAfgDcOqwQACil/gz8PmeCZY+TAHtYIXD5EbAlR/LkLUope7YrBDNBKZUAHgAudZNuAHqHFQI3Tzvw1RyIp9Fo0EpBOlgDLAYeG2Pb54Dhr+caEXnA7V5/SUQ+46YvcNeViGwUkSdFxBKRRSJSLSJ/cMu8ICIfHq5YRL7olntCRB4RkZWjGxeRK9yu3udE5EduF+2rIrJmRJ6lIvKY23X7VxE5b1TZZ0TkDhF5XUQOjrGPzUCFiHzJVZBQSh1VSv1iRBvr3XqedX/Xj9hWLSL/5W57UUS+JyLBMfblYRHpEZGHRpQ77tiIyDXARuBSt8v6n8Y6aSKydoQ8T4jIShHxicg2EYmIyC/cfNeLSOeILvFL3faeFZFHRWTZOPX/yu06v8hdf8g9x4tEpAT4rZv+tLucLiJb3S/r4TpSuWY+IyJ/kWQX/XljyeKWWS4i/z3ieF3qpp813K6I3Ogej20ismK8umaIF0i4/z/K2PfN48B45+1K9zp5QpJDdOe6196AiOwUkQ0iUiUir4nIQRFZPda9IiIXAjcBZ7jH//tu/eNdV6OP0/Mistk9nz9yj9l9I+RcKcl7+UlJ3lcb03cINZoMopTSywwW4BpAAd5J8v0F+Lr7vxJoBd7lri9y67jWXf8KUEfygfkNN60O6HLzFrr//e62/5dkN+hY7W4ELGC1u/5JoJHkw9kEdgKfc7edBnQCRSPKhoGV7vqd47RxI8kHfSPwbWD5iG0lbp0Xuesb3PVSd/0x4F/c/z7gNZJd/wBPuzL4gF8DZ46od8xj465/neSww3jnogToAN7trl8G7CapJFcAEaDB3eYB/uD+XwIMAivc9U8Bu0h2mQP8cvgcu+uNw/vtrqsRMi4C1Ci5LiI5/DCVa+bj7vo/AI+Os78eV86N7vpSoB9YOqLdOLDBXf8BcO8Ex28jEHPPz8ilDfj3UXkbgS+MOO5bgX9z1yPA303xfmsHatz/V444Pv8X+PGIfF8BLmaCe8Xdj6dH1T/RdTV8nM5x1/8IvOrul9+VbXjbfwLXuP9rgT9n6hmkF72kc9E9BVlAROqB9wA/B1BKdQKPkHwojeQhd/t3SL6g3gf8zE1rBZ4D/gawcZUIEQkB/wb8xwQivKXe6d7/HTAPOBc4h+QL4tduG9uAI8DlI8ruVkrtcrffMFblSqk7SPaW/Bj4ELBTRIbHlS8H+pVST7t5nwN6gCvc4/I+4BfutjjJ3pWOEdV7SQ7D/EQp9Tq8fTzHOzapcDkwqJR60i2/ieSD+2ylVBfwKPBpN++l7jpu/ZuVUnvc9fuBhcC4X+jTZQrXzH+7v9tInoOxOJukQvPvbl37gZeBvx2RZ9A9N5PVNUyHUuqikcsIWUZzoyTtQx53lzGvoxTpBv5OREqBPwG3u+m/Aj4mIgF3/WLgGaZwr6R4XQ0opV5y/28HDiml+pRSMWAPyeM8LOdHRWSRUqoNuHoG+6zRZA2tFMycYTuC+gnyDBtkjXzZdYxIB0Ap1TdGmV8NdzGTfIEXKKUiwIXucpCkkWPxBO33jGjDBnpJfgU1kHxgPj6iDT/JL59hRso0LkqpZqXUbUqpk4F/BW4bsR8do7IP7/txx0UptVUpNTQi741ADXDViLRxj00qsrrly0d03T/tyjBsFf8r4Fr3/8dJKlLH7Yt7LHsYdR7TRKrXTL/7N0qyR2W8unqUUtYEdfWP+D9RXdPhDldxOEspdaN7/ULy3pnovhmL97lldpE8L3UASqlXgRaSyuZpwHallDPFeyWV62pgxH9rjPXh4/Zl4A3gSRF5jqQCrtHMerRSMHNeB/YCl4zeICI/k+T4fZObVDVicxXJ8fjxGC7z0RFfYuuA2yVpxX1UJa28VwDlwHcmqKt8hEweoJRkV3QTkBj1tbcWuG/MWsZAROrHGLd/gHcUiyaO3W94Z9+POy4iskREykbkvQv4GLBxxJj5uMcmRbGbgOZR+72Gd8a3HwGqxZ1WqZTqHWtfJDlboIzxz2OcpJKF+2U7FaZzzUxUV5l77mdaVzr5HWPfN1eLyM3jlLGUUl8i2ZPRTnLIZphfk1TmrnX/M8V7ZabX1UhKlVK3kFQq7gX+JCKpKq0aTc7QSsEMUUo5wBeBr440OhORzwKrga1KqRaSL5yN7rYKkl3YvziuwnfqHS7z6RHJPyLZLVoP/MTN10dynNacQMwVIrLa/f8Jkl9UL5LsQj4sIle5cnlIjpNOxcjMC3xORsw9J2lA9qz7/xGgSETe5bZxHskX6cNjHBc/ybHYkV+pYaXUYZJGYT8XkcAkxwaSX28hSfLgGDI/QtI4cr3bbgHwFK4i4w5j/I7kC+e/RpS7H1g34jxfAxwCXhjn2BwETnX/f3DUtgG37ZCI3CQix3xJTueamYCXSX6Vf9KtawnJIYXfTKOudPJdkufpS8MJkpyqeRvvDNmM5hERMd0egM0ce93/O8mehNVKqbfctInulQEg5Lb7AEklY6Lrair8QkRqlFKK5L3gJdkrp9HMbnJt1DBXFuAC4EmSD4DnSI5LVo7YXk1ybPxZ4CXeMXYqd9cVSWOtVWOU+au7fM1NL3Drf86t7zFgwThybSQ5tnqXm38LsHbE9qUkx4KfcdsYNjp8N8ku2l7gsQn2OwTcSlLJeMr9/R1QNyLPWnffnnXbOWvUPv6Xu+0Fkl9pkDRY7HVleDdJewWH5Hj32vGOjVt2GfCWK8uN48g9LNMzbtuXj9p+NsmXhGdU+iXA826ZR3GNKoF/Jmlo1wh83k3bQNKA8S/AZ9xz/BJQ727/jXs+HsdVIEl23f/XFK6Zh4AFI8r+apz9XQr8ecRx/oCbvmpE2XuBs0ac92+PUc+n3e0x4IkR6d929/8ocJeb9oRb727gm+PIVU7ypT18/TzBCOPMMfJ/15X/afe8nz5q+1+AL49YH/deIamcvuaez7snuedGH6cr3HPdBnzJPf8jr9fPuPU+SdIY8ZpcP6P0opdUFu28aI4j2kGL5gRCRP4DuF4ljfs0Gs0U0cMHGo0mrxGRchG5zB1i8WmFQKOZPlopmMOIyBW846Dl+7mWR6PJEH7ghySHwb6VY1k0mrxGDx9oNBqNRqMBdE+BRqPRaDQaF60UaDQajUajAZI+0fOSyspKtWjRolyLodFoNHnFli1bOpVSox2KaTRAHisFixYt4tVXX821GBqNRpNXiMihXMugmb3o4QONRqPRaDSAVgo0Go1Go9G4aKVAo9FoNBoNoJUCjUaj0Wg0Llop0Gg0Go1GA2Rw9oGIvEQyohiArZR6j4iUk4xNfgBYTjIC2VE3/41AMcnIZY8ppR7OlGwajUaj0WiOJ5NTEv9bKfX1UWm3AX9RSv2niHwIuBP4tIicDVyslPqgiHiBHSLyrFKqN4PyaTQajUajGUEmlYLVIvKPQBB4RSm1CbgMuNXd/jxwn/v/cpLx1FFKJURkJ/AuICO9BZajiDpOJqqeGKUwlcJQDgnDBJHsy6CZE3jjcUzDRDCydhkpwHFsFA7KAMc0sJW+jnNBocfMtQiaOUomlYJvKaU2i4gJPCsiA0A1MOBu7wfKRMTjpu8cUbbfTTsGEfki8EWABQsWTFuwA4cP89TWrdMuL4Dp9WJ6PIhhYCA4joNt2TiJBOLYYNvv/No22BYjH50KUP4Ajj+AEwhi+fzYPj8Jj5eYx0vc9BA1TCJiEEEII4RVstyksqHwiGCSPMGmuGmACRgo2pVBVMfCylv8jk19LEpNZJDySJjCSATf0BD+RBQzFsWwEhiGB4/hwTA9mIYHQ0xM04MhHpRSOMrCUTa2bWE7No5KYNs2jmNh2Ra2ncBWFrYVx7YTjA6eJgZ4Aibi92EEvIjPi/Inf/GaKJ8XvB6UaeB4TZTHRBkGtmmAV4EZBezcHMA85+qT/gbT9OZaDM0cJGNKgVJqs/tri8hfgYuBdqAI6CVpP9CjlLJEZDh9mGI37+g6fwz8GGDdunXTfqUFh/ooe+Ol6RafEMPrw1NQiBEMYfiDiNeH4zNxxIulFAnbIZZIgFJILIoRi0J/L74U6h5WJFQgmEwYrXg4NpJiD4gSwaqsoa+8iqPBQg5jktBKQt4QM0wOBAs4ECw4Jr3YVpTEIRSNUxweJBQeIBgdIGRH8McHMQYGcML9qER8xjIoBxJhG8IRIDLl8p6iEgpqSgmUe/CELAxfFK83gukZBPpQTh9KKw1jIvKJXIugmaNkRCkQkZXA+Uqpn7lJy4E/AJuAc4Em4Hx3HeAR4F/csh5gFfBsJmQDKIrHWds9CJaD4/Ph+LzJxePF8ZrYpoltGtiGgSOChcIWwUZhOQ62cogmEiTiMRj19eQk4sR7u6G3e8y2DSAoQrB+AU5RGX3RGE6KL3IBJBaFWHTSvJPWpRTejjYqO9qoBFYZBonqOnrLqmj1h2hWhn4c5yH9ptAfBIJ+KPMDFXiVoiwBBTGFRCzigwniiemfXQFUJEKlGaHCjFNqxigxYhQSJUQcvxPDa0fxOHFsBxK2geVAwgbLViQsxeBgFGugj76BPvrceg2/n0BVLRQsIG54CMeiBII2hUU2wWAcvz+G1xvGMAZIKiF2clE2CguwUcpm8v40jUYzHpnqKegHLheReSS/+puA+4E/A98SkRXAUuAGAKXUyyLylIjcRnL2wfWZNDLcW6f44QeH8DgG1ZZBVdykMq4ojdgUR2wKhhxCAwm8A1E8AxEkNvZXlVVSSby8Equ4hGggSMLrJWpAwrawE2Gs+BCJ6CD26K8ypYg0HwIOEfL5CcxbQCJYQF946l9b6UIcB1/bEarbjlANnObxEqupo6ekghZfkBZl6EdtnpIQod0H+ASKfFCdSr/UxAScIgqGFAc7InR0RVBjXB2ioNYfpT4YptYTpsocpEIGKaWf6kQndgI6VTWdkQCdvXEi4Sjh5nfc8vsME19lFXa8nF5PMYPxBAnLmlQ2wwDDUJgmmOY7/4/9VXi8Nh7TwTRtTNPGMG0MI4EhFmJYiCQQ4kAcRRxUDEfF0EqHZi4jo8cJ84V169ap6QZEeqXtFX74xg9Tzl9ge6hOBKmKByiPeSgLGyzaN4CvrWfM/I4/iFW5kFhpHbGCKmLeIHHDIIEDEgeJEA83MdTdekw5b0ERvnnzCRtehqIz7w1IJ8rvJ1I9j+6Scpq9AdodbVymSVJiKyr7bAaOhukdjKVcrsEf4eKiZk5jL3Xh3cRUgE6jgc54IZ39Dn194eN64nwlZXgrqlBeP8owcBBsBZZySFg2lmVl/JXt8Sh8PvB6FR6Pwut18HoVhmnjOUbBsJKLJBBJgCTAVTJmaktx+mnfxzCmZ1MgIluUUutmJIBmzqKVghlw5mAF5+/zUr6rFbEnHwJQItjltcQrFtFWeSZhx8HnbyHSt5/owLEKhr+iCrOyln5bEU8kZixruhlctIxXSmsZyM/LR5MhquOKot4EnW1DRGKTf9UP4xGH84q7ONd/kKXx3RSFD2NJkE7PAjqtMjoHDbp7w9jWxC9ThWD6fXgCISQQxPD5EI8P8XhQhonjKhKOUigRlFLuQjJNKRx3UY6DM0ufj5/61KfweKbX0auVAs1EaKUgDVQkAlzSUsHS7d2YvYMplxtcdSFNRacTjQmBgkEMo4nBrv1YsXeGERRCaF4DqqScvlgcOwXlI1sov5+mFat5wwjoDlXNMRhKMS8K3u4YR48OYU3xup3ni3JxcROny37mDe3CYw3hYNDjnU+nU0V/3E/ENojEIZ6wsWNxEvH4cTMk0rMzJoZpgmlgmB7E9GD4/ZihQsQXwPF4sBDitkMsHs+KIqGVAk2m0EpBGhEFF/TWsG6PQ9H+o8d1fY6F8njpOeNDNKv52DYgDqHCXpR9iP7ORpT9zteWeLyEGhaSCBbSPwUDxUwTr65ja/0S2vSQgmYMfA7MG3KwOyO0d45tfzARJopzijs513+I5dYuiocOHTO91xKDvkAJcYqJUkREBYgqPzHHS8wSHEswE2AkHGzbIaEUlm2jUDiOwlF28tdxcJSTvK+m+VxUCL6CQsyiYoxgCHx+HMPEUkLMtojFU+/1MwwDQwQRwRDBMJL/BbjqYx/HNKfnq0ArBZqJ0EpBhpgfK+S9TSU0vNmOEZ7cPsAurqD91A/RFi55O83w2AQL2klEDjLY3XLMg8rw+AjVNmAUlxJRQn9kKDNfSSmiROhZfgqbQ6XE8/OS0mSBIhuqByw6Dw9MaXhhJDXeGFeV7uHs6PMEYl2T5o+aPjoLSukMFDIoAVTcj2MZOHFBxYC4gz/qEIwqfFELb9TCE44jcQscBaaBY5oo04MyTZRpYAcCxEMBYq5xcdSxCMdiyRlJE2GY+IqKEZ8PZSenEzuOg7Itd0n+n0wpufqfvoHp0TYFmvSjlYIM43dM3tNVw+odEQLNnZPmj9WvoGXhe+gNH2sh7vXH8QVaifTvI9p//HTHwpIaglW12MECBq0EveH+tO3DVLALi9m77BT2KO1xTTM+hQ5UNIVpbR+adh0miivLD/E+XqJscP+061Eo+v2F9AaK6PGF6PX66PF46DOEQUdBAogqvHGhOG5SmDBY0GpRurs1qTSMwA74sEpLiBcWEg/6iXo8xEQRsSwisQh2CrMnUkErBZpMoZWCLLIqXMaFBwJU7WhDEhM/HIZWnk9T6Voi0eO75P2hITyeDhLRNoZ6W48ZYgDweHxU1SzDLCkj6jXpiQ0xEEnd1iEdhBcs4dWKefTOjhEOzSxlSb9N277eKdscjObsoi6uCrzK/P7XMVRmPGxYYtAbLKbXX8hrRaXsDsd498FC6re1jTtt+bg6CkMkSoqx/YFkz4NhguFFeTwoMVCG6aZ5UIaBkuH0Ef9FWP/Zj2BO09WxVgo0E6GVghxQHy/k8w8OIZN8NSiPh97TL6NZFjFeVhGHQMEAhtFBPNLGUO9RGGVrUFpSS3nlIpxQAYPi0BXtZSgWTtPejI/j9dK6YjWve0Jo3UAzHmWWItg4RGfPzP10zA9E+GTRNlYPvYjHmn4vRCr0Bop4pGYhr0X7eU9rOSdv68Pszk4P3YKf/gTxTc/fhFYKNBOhlYIc8Zn99Sx66XBKee2icjpOvZzWaNmkflPEcAgW9oLqIDbUSqS/85jxSdP0Ul99EoVF1Vh+PxHDps8O0xPtI5YG17djkaio5s0Fy2nWhoiacTCUYnGPTfOB3rTYxoRMm0+U7WFD4gVCkbY0SDg+naFSHq5q4MVYBxd0V7N+l0Wo8Tgv7WlFKwWaTKGVghxRaHv58iOCMZj611G8bhkti99HTzj1h4HhsQgEk0pCdPDIcf4QxPBQW7mYyqIGTF8BMY/BgBGlxxqkJ9KHZadnDFQBfctXsbmgXAdi0oxLTRyc/X30DaZHQRUFl5Y380FjM1UDOycvMAPaCit4qLKOzbF2Tg6X8e59Acp3tKTkw2SqaKVAkym0UpBDrjoyj9VPN025XHjFubRUrGUgMvUxRY8vjj/QC/RhJ/qJR3qIDvUdM+RQXjKP6rJFFHsrsD1ehkyLPiNMjzVAb6R/RlMhnVABB5afyi68ekhBMyZepZh/NE5zU3q74lcX9PHx0GssHXgFw8mcQ7Dm4mr+WF7Na7F2ahIh3t9UxsJt7RhD6fNSqpUCTabQSkEOMZVw02MFeDr7Js88BuEV59JSuZaB8Awt/cXBH4hhesMIAyh7gESsl+hQD3Y8RihYTG3lMsoCtQRUARHD4aC/gyP9R6fdpOPzEa2bT0dxOY2mn778vAw1GWR+RNG/t3faUxfHo9oX47LiRlazl5qh3Zh2ZlyKN5bW8YfSMrbHOvE7Jpe013Dq9kF8R8d2jz4VtFKgyRRaKcgxF3fX8K4/t8yojvCys2irXk9fOP3xrTxeC69vCMMcAgax4n048SFWVK1BeQvYQTO94ekpNSOxyqvoq6qlJVjE4TyO0GgCfnEXFD4UPqXwOg5enOSvY4MPYj6HfuWlz/HRaxtYSttcjCbkQNWRCK1tmZk94xPFBSVHOcvXyNLYLgojR9Lexp7y+TxYVMjueNKnwrm9VZze4qX0aBjf0Z5pDS9opUCTKbRSMAv4h+fKCR7qmHE9kaVraas56zgfB5kgVNyON9HE8pIz6fLH2Rk7TDSeni8u5fMRqW2gs6ScRjNAb4YvUa9AgOSLfPgl7sN9kSsbj/siN20Lj21jWhaGlcC0EhiJBJKIJ5d4DJnC0IqIoqbGpqy8F7+vhTAJwmY1Q0YVQ0YZyXiCBQyoEH2Onz7HS799YkarXDzg0L63h0SG3Xwv9Ee4qOgwp7GP2qFdae1FeKtyIQ8WBDkQf8fPiN8xWRkpZWlfgHmdDsVHB/F29E3qvEgrBZpMoZWCWcBpQ+V85KHOabtWHU108Zm01p2TceVADIdQ4X5KRaj3reBwUS97+5uwnfR+51tllfRX1XIkVDxhL4JfICQQQhFQDkHHxm9b+GwLbyKB14rjiccwYzGMeAxJxCAeR2bJPRAKKWpqwxQVdoIcRqnjjVAdPEQ9NXSYJ3HYWME+u4qWxPSc2OQbpTYUNA7S0Z2dEOM+UZxb1M65gUaWxndRFG5OS71bqxbzbEGI3Yk+Is7xBpWFtpeTh0pY0hegptOiuG3guKmOWinQZAqtFMwS/vfrtZTtSG/XZWzhatrqz6M7HEhrvaPxBaJ4jLdYWLiEoCpnb8FRmvozMw1MebxEa+txTA9mPIonFkOiEYxoeEpf6bMdEUV1tU15RR9+Xwu208Z481GjZhUt3rU0yjL2WuV0WukfRpotiFIs6bVpOdCL7WT32fVOqOd9NPS/xkwHexyBxpI6dhWVs9NU7I33Eldj20+UW35OHiphUY+X6k6LU/7hGxhe7dFQk360UjBLmB8r5LMPDmRk+lJswSqONlxAV4aVg1BxF2b8ICeVnknUEHaYzXQP9Wa0zROFUEhRUxOhqKgTkcM4anznU0OeBpq9azjEYvYmyui1jRm3b6IoMR2KzQQlRozGRBF9aah3ulRYEDw8RHtX5p1wjcX/qXqK5X0vpLVOSwz2l9ezM1TMLsNhf7wHe5w5Ove+9168plYKNOln7n5S5BlN/kGOrGmg4ZXUHBpNBf/hHSw4vIPa+pUcXXQBnUOhtLcBEO6vQIwydkYaKVYWZ/lOpqMozI7YISJpsjc4UQmHhYMHQ8ACRBbQ0BCnrPwQSjUyugehwGrmJKuZk4BLgH7vUpo9Z3JQLWBfophB552XuQAFhkOpaVFixCmWMEUMUkgfhaqXAqeDkH2UgOUOb7kfsraE2Br4GE/HlhDNgYFklwdYHGJRVZDuA71E49k1Tb2n9zy+492Kx0qfUuJRDid1NXGSG+MpbnjYU17PjlARu0hwKNFzQtqTaLKL7imYRZRafv73n2wkPEmktRkSn7eM5kXvz8hshWG8gRgeYwcLCxdQalVzqKSXPQOH025vcKJTXOzQ0NCF17t7wt6Dt1FCj+9kLAkSdNopsNoQpj9nP2ZU8rL/Y7wQrcWecYf69Ag5itqjcZqbsxsE7H9Ubufi/oey1l7YG2R3WR07giGuedf/waN7CjQZQCsFs4yPNdWz6tn09xaMRonQd8ZlHDaWYmfwPR0q6sFI7GdF6RkYlo+9Re0c6pvZFEzN8ZimYsGCMMUlB3Gc7B/fAc9invN+mNeiZVlve5h5MYV1YIDewcwq1cN4xOHe4vsoiOTgev7UH8CjDQ016Sd3g4KaMXmwvhW7vDjj7YhSlL7+CKsO/o7ygsw9RMMDZQzF1rA70kxT9C1OHqzhXf7VrCxZTG1RFb5pPtg0x2LbwsGDBbyx9VRaW94N6lREsjcrocg6yAci3+N/eP/Acl92ZgeMpsUvdK0sYv6yMjxm5h9tljK4nw9kvB2NJptom4JZhmU4vLy+iPMezU5XqKe7jYXP/4jyU9/LoeApJDLg/VUpg6G+RcT9cfqd12gI1THfqWKxVYrE5hMN2gwEY/R6IvRaA/RE+tMWc+FEpLPTQ2fnPPz+OhYsHCAU2ovjdGWl7cr4Vj7OVpoCF/GEcwFHsjxd0hZhf5mHsuIKKpvCtHVkNlLiX/pqubTyDBr6t2a0HY0mW2ilYBbyeGUbaxoqCTR3Zq3Nou1/4eSi12hdfRUd4YKMtJGI+UhwOs1GHy2yDyuR9I4YiocoTlRS6StlvlGDV+YT9SsG/LFkzIXE9GIu+Dw+/B4vpmlgGgYmPgQf4ngJ+BRha5C+6EDGokPmmlhM2LunGFjDvHkWlZVNKA7ANKNOiHgQ8QM+HKeXiUJ2zo8+zUb1DHtCH+IviTPpsWfoinuK9JjQsyjEwqoAffsIFJ7IAAAgAElEQVT7CKfZVfJI/m3wIm413spoPAWNJltopWCW8sQak8vS4yslZcyBbhpe+CllK8/nUPE6Yhl6V0YGS4CSt9f7Eg7RWIwuJ4xIC47VhxXrx6uEomAZS4IVBDyLSPhNwqbNADGUUnjEwEBhKoWybbAtDCWI8uLYBnHLIBI2ScQDWHHfMU6PYgIn182jLBIn5rEYDFkMeqP0E6YvPshAdAhHzRW/B0JLi5eWliUUFi6mYX4PXu8QyvHguIvteLAsA8c2sSyDREKwLJNEQkgkIB6XkTGzqK21qKl9HceZwI+/KFZEHmaJPM72wFU8GV9BJMvhsw8VGAROLaOhI86Rw/2oDNjvH4wWsKXq3azvezTtdc8WtmzZ0mAYxmOO46yEHFmUatKBMgxjl+M4l6xdu3bMN4xWCmYprxZ1smHlPEp2Zd+IqWDX85wU3ErHGR+lNVKa+QaVQSwShEgQqHg7OQHE4nH6iWKY/aihAex4H8qKoMTA4yvC8BSjKMS2ColHgygntbFkpWBHyxDFBV5WFgSp6I1TgZ9hZcURxVDIYjAQZ8CI0u8M0RsdIJbIjhFbphgcFHbtLAfKZ1RPW5uHzs51nLTyKIbxJhP1GnhUhDMiv2GVWcYrwY/xXLQ+q3EeogYcqPFRU1aJHByguz/902N/2H0mp4VewR/rnjxzHmIYxmO1tbXLa2pqxDC0KVq+4jiOtLa2nnTo0KHNV1xxxcUPP/zw7tF5tFIwi3nolAjX7jGOCWucLczIELUv3kfJkjM5VH0BkWhuPg7suI9I3Accb3yZSEOPcP9Qgs1DCRZVB5lnOYg7391QQtGQl6IhL3UUMKysxHwOQ6E4A94YA0ToTQwwEJlLvQqpY1nCW9trqa2roKbmdXdIYXx8dg/nh3/MGZ4FPGR+ioPxzDrTGs1RHxgrClncF6LjUF9afRuEbZOHvR/gY7HfpK3O2YTjOCu1QpD/GIZBXV2d0draWgfcdMUVV3zz4Ycf3jMyj1YKZjEHA/20nllP3ZamnMkQPPA6JzXtoGPNVRyJV0/0QZjXNLZHOOIxOKUmSKgvNm7/qD9u4I8HKCdAslehFkcU4QKbQX+MATNKv53sVYjmea9CqrS1eunqXM9JJ7UhxpuT5i+wDnON/V0eC3wp61MYHRH2l5p4S8qoH1TEj4bp7EnPbIkHuhdxcflJVA4e9/E1F9AKwRzBMAxEBCAOrAe0UpBPPLC0m/+53YdkaoA/BSQRo/rl+ymtX8mhBe9lMJJdo7FskbActh4ZoqrUz1KfgRlOzXDMUELhoIfCQQ+1I3oV4l6HoVCCAV8saauQGKI/OjBlg8l8IJEQtm+vY968SqqqX8NxJg6nbaooHwjfRXnoc/wlujBLUr5DQoTGIoGiQqrjBRR0xTnaOog1QzfjP469l6+yB5mr2rPLJ378Ylrr++0Xz500T1tbGzfffDNvvPEGr7zySlrbT4XZss8HDx7khhtuYP369WzdupVPfvKTXHHFFdMRwQKCoxO16jfL6fJG2bu+NtdiAOA7sotlm3/IfF9rrkXJKB29MV5qj9BV7EeZ0x828SUMyvr8LOgo5tSOWs7vXcr7Y2dwofc0aouq0ijx7KGlxcvOHWeBOnXyzKI4O/IzPhZ4FTOHL9F2n3Cwzo9zRjkNK8opKZy+74xtQ6XsLL0gjdJphnnuuee48soryVeHe9NhrH3+9re/zYYNG7jpppv4x3/8R77yla+ktU2tFOQBf2w4il1SmGsxABDbpnLzf1IRmvuxDHa1DPFGXBEr9qetTkNB4ZCHNZ0NnFKydLgbb04RjwtvvjmP7q6LMIzJHXGtiDzMRt+fKTBy24MSNYQDJSYdK4upXF3JvNrCaZ2fe7rPIeGdHffrXOKjH/0oRUVFuRYjq4y1zzU1NXR0dADQ0dHB2rVr09qmVgrygIhp8dpZuXMfOxbzdj6EOTdHEY5hKGLxassQTUEvyp++HRYRFnWUcJ7/FIK+7BrcZYsjR3zs2nk2qFWT5q2NvcTn5ddUe2aB0yoRWgJC4/wgvjMrmb+klJA/9ZHWbsvLk8FLMyig5kTm+uuv5+WXX+b666/nG9/4Bp/97GfTWr9WCvKEP1e1EK+b2TSydOLpaWOBOpBrMbLG4Y4Im/viDJT4SedsutJ+HxfEVs7Z4YRYTHjzzQZ6ey7CMCb+yiuy9nOtfQ/LcuQmeSwGTNhf4WVgdSm1qyqorkgtwugvO06iP7Qgw9JpTkQ2btzIF77wBb773e/y4IMPcs0119Ddnb6psFopyBOUwJPrZlecgJLXH6E4NAu+7LKEZSm2HRlij2HMyNZgNN6EwZrOBk6do8MJAE1NPnbtPAc4ecJ8fqebj8fuZH0gO26ZU8UW4XCBQfOSAorOqKIgMLH7ZiVwn6N7CzTpp6mpibq6OgDKysowDCOtxstaKcgjXi7uYGB5Xa7FeBtRivmNjzJH32Pj0tkXpz2YXp/+IsLCjhLOn8PDCbGY8Oa2+fT1XjhhsCYhwSWRu7k0sD+L0qVOlxdKFk1uK/F8fxWNJeuzINGJwTPPPMOvf/1rWltbueWWW4hEZk+PUqYYa5+/973vcc8993DbbbfxpS99idtuu43Kysq0tZnRKYkiEgReBh5TSt0gIgHgTuAIsBy4XSm1x837KeBMwAb2K6XuzaRs+cqfVsf45H4BZ3ZY4Ppa9lE//yjNsZpci5JV9rWFKZtXgK8/vb4ISvp9XOBdybbiI7QNdKS17tnC4cN+HOc8ysr/ykRxGNZG7qM08AF+Hz8nqx4QU6GxUKgrCdDVN7HB7T39F/AtcxumPbd8VqQynS7dXHjhhVx44YVZb3eY2bLPGzZsYMOGDRlrM9M9BbcAr49Yvw44rJT6JvA94GcAItIA3ADcoJT6B+ALIrI8w7LlJXuDfbSf1pBrMY6h8rUHCQZmh5KSTd7siqK86b+FToThhOZmP+HwOZPmWxr9M5/1PkyROct8O4ggCyafYdAcC/JS4XuzIJBGkx4yphSIyKeB54GDI5IvA14EUEq9CZwuIsXA+4Et6p3JmC+CDlQ+Ho8tzWw42KkiiRgLO17ItRhZJxqzOeLNzBSME2E4Yf++QixrzaT5qmNb+By/oNY7u+xXWgJCXe3kisG9nacTCVRnQSKNZuZkRCkQkVXAyUqpP4zaVA0MjFjvd9PGSx9d7xdF5FUReXV4nuaJyP5AH3b55GOa2SS4/1VqQv25FiPrHGqPEClJnx+D0ZS4sxPqiufm7ISdOyqYzPgQoNA6xLXW/+UkfzjzQk2B/roAxiS9OXEl/N7U3zia/CBTPQUfAaIichOwAThLRK4D2oGR85KK3bTx0o9BKfVjpdQ6pdS6qqq5+ZBMlaNLshC9cIrUvPEg3vTa3+UFbx6NpNWHwWi8CYMzO+bqcILw1vb5GMaiSXN6nV6ujn6HcwKz54OgxyPUL5hcQd/U08DRolOyIJFGMzMyohQopW5VSn1DKXU78BywWSl1F7AJOBdARFYDbyil+oFHgbXyzhPvXODPmZBtrrCjZnZ1pQKYQ70sjG7PtRhZJ2E5HFSZjRU1l4cTHAd27liOYUzexS4keE/k+1we2Dlu0Kps01rpxZ/CMNIPI+/BkRPA45cmr8mooaGIXA28CzhHRP4GuBtYKCI3A18BPg+glGomOSvheyLyHeCnSqm9mZQt33mluAPlm32f5UVvPkF5wdyytE6F1u4YgxkcRhimpN/HhvhKCgMFGW8rm8Tjwv59p6fkFhng9Mj9XOt7goCRewPXsCFULyqZNN+ucBFvllyUeYE0mhmQ0SmJSqkHgAdGJf/PcfL+O/DvmZRnLhE3HAYW11C8uyXXohxH/a5H6F14NXMwGOCEbG8d4uyKAEYks704vrjBOs9SnjN3YNmzr8dougwOCk2H19Mw/zmUmlyxbIg9wxe8rfzO+AQdVm4DvjaWmJQV+Ogfmjia6Q+61vL94Kv44hNHkZz1/PLy9Na38ZFJs+zfv5+bb76ZNWvW0NzcTEVFBf/8z/+cXjkmYhbtc3d3NzfddBNLlixh79693HbbbdTUpGdauHZelMccaJidka89Xc3Ml0O5FiPrOA7sjTlpdYM8HgVhD2sCc2/Wbne3SWfHeQipdbOXJPaw0fl+zg0QbYFQCg6N+mwv/+3Xng6nQ3d3N5/4xCe48cYbufvuu/ntb3/Lli1bci1WRhlvn7/2ta/x3ve+l5tuuokPf/jD3HDDDWlrUysFeczm8p5cizAuZa8/TFHQzrUYWaezP05vUeaHEQCqeoKcXLI4K21lk5YWL4ODqTuK8dk9XBW9k/MDbRmUanIOh4Sq8uPC0x/H/Z3LaC+aPEiU5ljWr1/PlVde+fa64zgUFMytYbTRjLfPmzZt4txzk/fI+eefz6ZNm9LWplYK8phWX5h47ewJkjQScRzmNz3BrLEGyyI7WoawCrNj77G4vZR5xXNvDvyBAyES8dRdBBtYXBT5AR8ObMPMqMnnxFjzC5BJLnolcGv/B4n7JrdD0IzNgw8+yPvf/35WrlyZa1Gyxsh9bm9vfzukcnFxMT09PVhWeoYStVKQ57Qsmr1x2/3NO6n3d+ZajJywa8BKa9Ck8RARVvfMozg4e6+D6bJrVxmoU6dU5pTI7/mM71EKjNwYtBz1CfPmTX4ujib8/Nz8GOpE1JpnyFNPPcVTTz3F9773vVyLkjVG73N1dTUDA0nXPv39/ZSVleHxpGc4WSsFec4bNRP7Xs81la//gYA/9xbi2aZvKEFnKDu9BR7bYG1iKV7P7JuNMlO2b6/DkCVTKlMXe4HPy30584DYVRvAY07+aH26r4bNpe/PgkRzh02bNvHoo49y991309bWxosvvphrkTLOWPt82WWXvb3vzz//PJdddlna2tNKQZ7zRkEXTmj2zls3YhEW9m7OtRg5YU9rmHhxdsJdh8Ima/1zz/BQKWHHjqUYRu2UyhVZB7nWuotV/sEMSTY+/SbUpeDQCOCuo2vpLDwpwxLNDbZs2cI111zDSy+9xMUXX8yVV17J7t27cy1WRhlvn2+77TYef/xxbrnlFv7whz9w5513pq3N2Wm+rkkZJdCzpIKK7UdyLcq4hHa/RPV5p9Aenntd3JOxozvG6UETSWS+O7uiJ8CqqiXs6DuQ8baySSIh7N2zmuUrIjhO6lP5vE4/H47eSXXoCzwdyW4QsaZyL8EWD5HYxL0VSuC2wcv5lrcVbyKP3ISnMJ0u3axdu5bBwewreW8zy/b5Jz/5SUba1D0Fc4C982b/uGTtmw+SpiGvvGIoatOSoaBJY7G4o5SG4ql9VecD4bBwqHEdyWjsqSM4nB/+MR8LvJpVA8S4AeUpTFEEaIkH+JX3ozk0j9Ro3kErBXOAl8u6wZjdioE50M3CxM5ci5ETGtsjRIuzM00R4NSeOkpCRZNnzDN6e03a289J2YfBSFZEHuZzvocpyqIBYmORQWmK01Mf763j9VIdYlmTe7RSMAfo9cSIzK/MtRiTUvzGY5SGJvb4NlfZ3pHZoEkjMW1hbWwJPk927BmySVurl77+85jOXNfq2BY+Lz+lwZuda1CJ4FuUunL2nfaz6C6ce3YhmvxCKwVzhKYFU+tWzRUN+zZhnIBXXSzhcAjJWhdxMGKyzrt80jnz+cihxiCWtWZaZQusZj6V+C7zvIk0SzU2zQGhtio1Bzs2wjfDHyLhPfFsbzSzhxPw8Tw3ea1qKNcipIS3/TDzzeZci5ETjnRFGcpC0KRhyvr8nFqyNGvtZZOdO8oxZHreHE0V5gr+mDUbg3BDKGXlrCka5D982r5Akzu0UjBH2B3sxS7Njy+M0jc2nZBGhwBvtYVxgtnb+QUdxSwsmZe19rKHsGvXMgyjbFqlK+Jv8p7AwTTLNDadHqifn/owwp976tlW+u4MSqTRjM8J+miem3QsLqP29RxO2UkRIx6l1jxKs5WeqF75hGUr9iUclgtIlj4HT+6qob9kiJ6hPI/MN4pYTGhuWkN9w7MoNfXhgHWR37DL9w8cTmS+96a92o+31SRhpRYP5I6Os7mntJHSodk5vfRzj34urfX9/P0/TylfJBLh7LPP5pJLLknr3PxUyMU+jxcl8ctf/jKhUIjCwkLeeOMN7rrrLmpr0zPrSPcUzCF21uVPAKKyPU8jc2+4OyU6euN0FWbPCNB0hLXhRfi92Ru6yBZdXSYD/edMq6yQ4EPqgawMIwwaUJviFEUASxl8K3IFlmduB/yZKjfffDNnnnlmrsXIGuNFSSwoKODWW2/lq1/9KmeeeSa33npr2tqcVCkQkRIRCYqIX0Q+LCKlaWtdk1ZeKe5C5Um/vKenjcpgbsPd5pLdrWGiWbQv8MdM1pnLMWTufQccPBjEcU6bVtnSxC7eH9iTZonG5nCpSWEwdVfUB6MF/D5wVQYlyi9+/etfc/7557N48dyLDDoe40VJvOWWW45JKyxM39BxKk+IHwFLgW8DnwC+m7bWNWklYloMLq7KtRgpU3XkpVyLkFPeOJpd+4LSfh+ri+aq4WEthjF/WmXPiNzPYl/mY4gkRChenHpvAcAfuxewo/RdGZIof9ixYwc7d+7kqqtOXCVprMiQvb29PPbYY9x4441paycVpWAL8BZwrlLqE0B21GrNtDjYkD9BcfyH3qQolD9DHunGshQ7I3ZWoikO09BZxKLS7Lr8zQaOA3v3rMQwpvbShaTXww/Zv8OXBSOPxpBQUTq1WCW3d2ygP7QgQxLlBw8++CCBQIDbb7+d5557js2bN3PXXXflWqysMVZkyL6+Pv7+7/+en//855SXl6etrVQ+U1YCXwOed9fnXvD2OcSrFX1MryM1N9QM7GTAnFp43LlE72CCluog9eHszJsHOLmjimCll90Dh3Cc3IQYzgThsNDWuo6ammdQTE3ZLLL284HgWzwUzfC1KAILC6E39Z6JuBLuiH2Er5v3YtqzOypqpvinf/qnt/9Ho1EGBwe57rrrcihR9ti0aRN//etfufvuu2ltbeXQoUMsX76c6667jjvuuIP6+noeeOABrr766rS0l0pPwc+BSuBWEbkcmJ3msBoAmvyDJKrzx+yjcOcz+Oae470p0dgeYTCL9gWGEpZ0lHGhsZrqooqstZsNjh71EA6fNa2yp4b/ixW+zNu5tPqEutqpjQHvjRTyYDA9D/185oEHHuDZZ5/lpZde4v7778+1OBlnvCiJl1xyCdu2beNv//Zvueiii/jlL3+ZtjYn7SlQSr0AvOCuPiIi70lb65qM0Lq4mAXtvbkWIyXEsqhVRzhMfa5FySnbWoY4qyaEZzB7bqBDYZP14YW0VVSyPdpILBHLWtuZZN++IlavXgWyY2oFRfFB+z84LJ8nqjI7pNNfF8Q4OoSjUh+y+H33IlZXbeCkvucyKFlqpDqFMN1cffXVafsiniq52OfxoiRu3LgxY22mMvvgAyLykIg8KSJPAT/OmDSatLC9Jr/iC5TuepI5aBQ/JZSC7b0xlDf7B6K2q4AL4yezuGTuKGY7dtRjGnVTLldgHeYy/9YMSHQsPR6onz91+4dvdm1gIDT3bEI0s4dUnkBfBf4F+Ky7/CqjEmlmzGuFnahg/sxJNwe6qQnkUSz5DDEUtTmYI+cN3oTBqo4aNgROnRMRFm1b2L//VAwJTbnsysiDrPJn3glYa5UPn2dqQbKijsl34lehTlQnH5qMk4pS8KpSaqtS6pBSqhF4KMMyaWaILYrexbM/auJIyg89P3mmE4DW7hjdWQyzPJqSfh/n9S3n1JKlmEZ2ojpmioEBoaPjbKYTUfHSxK8JGZmdjRA2oGZRyZTL7QoXkVD5fW40s5dUlIIXReQZEfm5iPwC+GmmhdLMnH0N+dUf7z+yh9JQ9izwZzM7W4aI5VAxMBQs7CjhQjmVuuL88XsxFi0tXuKx9VMuF7Rb+ZB3cwYkOpbDpcaUHBppNJkmlTfHl0k6LLoP+CWQ+QE3zYx5ubSbfPMjXNWzLdcizBreaI9k1bHRWAQjJms657O+8GSCvqnNrZ9N7N5dgsiKKZdbFt3E6YHMxotIiFAyBffHGk2mSUUpeEUp9ZBS6hml1DPA7ZkWSjNzurxRovX5Nd2sYNfzBPw6aCxAwnLYE3PAyL1iV90d5F2RlSwrWZByCODZhbBzx0JMY+pDau+L3UeRmVlfDgcLhIqS/FW6NHOLVD5FykTkPmC/u/4u4L2ZE0mTLpoXhljWnGspUkeUotZqpJETx7f5RHT1x2mrDVGbxWmK4+GxDU7qqGReUQlveg7nXcTFREJobDydBQufQ6nUp176nU6u8D3Pb+wLMiecCLKwELblj2OiQ9d+Jq31LfzVfSnl2717N/fffz/BYJBnnnmGr3/965x11vT8UkyVXOzzeFESh7nlllu466676OzsTJtcqSgFiznWjiA/JsBreL06zLJcCzFFSnY8ibnq89gnrvfjY9jfFqa4voBQ3+zwIVA04OVclvBC6QF6w/mlGPT2mhQVn01p6bNTKrco+jjrgqfwajR9rmRH0+IXFlQX0NY+lLE28h3btrn++uv505/+hGEYXHvttXjyJADcdBmOkjgcFGnVqlVcdtllrF27lqeffpqenp60t5nK8MFnlVL3DS/A36ddCk1G2BnswSnOr9CrRmSQam93rsWYVbzROoRdMHuM0QRhtT294EO5pulwAMtaM+VyF8fvozTDwwhD80JIntkBZZNXXnkFpRTf//73+eY3v8mf/vQnKivza5bVVBkvSuLRo0f57W9/y//6X/8r7W2mohR0i8h3ROTbIvJBoCztUmgyghLoXJx/p6viwDO5FmFW4TiwfSCRE8dG41E84GNJSX460dm1sxLDmDelMj67hys8T2dGIJcuL9TX57+PiExx6NAhXnzxRTZu3MhXv/pVnn32We67L7Vhh7nAcJTEFStW8LWvfY1vfvObGWknlafM7cA2wAFeAq7PiCSajLB7Xv4Z7nnbD1NekD/jq9lgMGxx2DCYTWdzWU8VAW/+OMkaRiloOrwKYWpz/edHn+acQHuGpErSXuPDa84e5W82UVxczMqVKykpSfp22LBhA08//XRuhcoSI6Mkvvbaa3i9Xu69915++MMfEolEuP3229m7d29a2krl6tvtDhv0KKW6gaa0tKzJCi+VdKLy8CFT1f56rkWYdTR3RenLof+C0Xgt4ZTAolyLMS26uw0S1ulTLveu2H1UeDJn8DJoCLXTcGh0InD22WfT1dWF7RocHTp0iBUrpj7VNN/YtGkTjz76KHfffTdtbW0kEgl+9KMfcdNNN/GlL32JYDDITTfdxPLly9PSXipvi1NEpA5QIlIC5Odg4glK2LQIL8o/BzShvZspCMydsL7p4q2WQeLFsyesZG1XAdWF+TX1dZg9uyswjKkZD3qdAa40HoMM9tkcLjUJBea2Ad10KC8v51vf+hbXXXcd3/jGN+jo6ODLX/5yrsXKKONFSQTYt28f99xzD5FIhFtuuYWhofQYqaZy5f0CeAUoJ2lk+InJCoiIAfwJeBnwAUuBzwFBksMRB4DlwNeUUkfdMjcCxSRtFh5TSj081Z3RjE3jfD+n7J8832yjJrqfA6RH+507CNs6Y6wp9WGEZ4cHyFNi9XRKD47KLyXOtoX2o6dTWfXUlMrVxV7kjMC5bI1lJkR5whDKFpUQ3tWVkfrTQapTCNPNRz7yET7ykY/kpO1c7PN4URIBli1bxp133smdd96Z1jZT6Sl4WSnVACwA1gGHUqz7RaXUN5RSNwMh4CrgNuAvSqnbgT8CdwKIyNnAxUqp/4+kB8XviEhm7rgTkC0VA7kWYVoU7XiSOT7jaFrE4jav98VxQrPj4ISGPCwvWZBrMaZFa6sX1Kopl9tgP5zSw3O6NBYKpUWzZ6hIc+KQynV9E4BSqpPkV/8dkxVQSjlKqVsARMQDNAC7gcuAF91sz7vrAJcPpyulEsBOkk6SNGngYKAfqzL/ximNeJQaM7OGXflKNGbzel8i566Qh1ncVUaBf+oRCWcDe/fWY8jUpu6WJPZxVgaNDpUIvoV6JoIm+4yrFIjIaSJyLXCGiFzr/r8ESPnuEZH3A48AjyilXgWqgeHP1n6S3hI9o9KHt1WPUd8XReRVEXm1o6MjVTE0wNE8NV4q3/tUvoVwyBrRmM3r/bNDMTBtYbVnUa7FmBbRqNDXN3XfBeckHsQrmbMtaA4KNZX5qWhp8peJegrKSHozHP5dTPKL/3upVq6UelQpdSmwWET+HmgHhtXfYpIzGqxR6cPbjlPDlVI/VkqtU0qtq6rKP+O5XLK9dnaMP08VT3cblcFwrsWYtURjNltniWJQ0ROgvrgm12JMi8bGIIZMzb12gXWE8wNHMiRRkmhDQZ7Gm9DkK+MqBW4ApH8FvqiU+ld3uUUpNamPUBFZJSKXjUg6CCwBNgHnumnnu+uQ7E041y3rAVYBU/NFqpmQV4s6Uf7Z4xVvKlS2ZD6EbT4Tidm8MTA7FIOTB2rxmLmXYzocOLAUkandI+uiDxAwMtdb0OGFefWFGatfoxlNKjYFl4jIOSLybhHZKiIbUygTAz4vIjeLyL8CJ5M0Kvwa8D4RuZmk4eENAEqpl4GnROQ24PvA9UopHWMhjViGQ//i/OxdCTS+QVFQB0OYiHDUZtssUAz8MZOVhQtzKsN0GRgwiEamNozgd7q4yHcgQxIl6awJ4MlDXyOa/CSVJ0i9UurfRORJ4JPAZycroJTaT/KlPxZ/N06ZSQ0YNTNjf4PJml25lmJ61AzuYsA8JddizGqGojbbgNOKvBgRK2dyzO8soamkiL5w/s162bu3hNNPr8N2WlMuc3rs9zxv3MiAk5kX94AJSxcU03Rw9nwn/fG7r6W1vg9fn5oydscdd9DY2EhlZSV79+7lZz/7GcFgMK2yjEcu9nm8KIlbtmzh9ttvZ926dbz88svceOONnHvuuZPWlxtbBkAAACAASURBVAqpKAUR13lRVCm1Q/5/9s47TpKqWvzf0zlMTjuzszknNi+wgKyACrIEeSoqIPIePlF5PyUK+HAFXCQnn5EHCBIUnoCAiwQRSS6wu2xkc96d2dnJsXP3/f1RPUvvMKFnpuPM/X4+9enu6jp1zq2uqj5177nniCSuRqMmpXxY1Mx8ESPPa5aRs+Wf2ObNJJCdoREpo8MXZoPAbLcVky89joFJwTGRsbzLprToHwxKwcGDM6gYeRgjs3vfWCIdnOrczAu+WUmz60CRFWe1Ba8/fc5euqmpqeG2226jvr4ek8nEueeey3PPPceFF16YbtOSRk9VEm+88Ua+853vcN555/H888+zbNkyXn/99YTojMe1LcOYLvg7ETkRI1eBJgs5bPXgr0he+ddkIqEQ5SQ3qGuo0OENs6EjhEpjVrz8VhvjCrKzYFJ9vZlIuH8pkGd6n09q+uOACYrH5SVt/9mAy+XCZrPR2toKQHt7OzNnDu3ew56qJI4YMYLOGXh1dXUsWLAgYTrjcQr+F5irlHoB2ARcljDtmpRTPS67SinHUrD1H4geWo2LDm+IDR0hIo7+Ff1JJFOaSrBbMyclc3/Ytq0Ekyn+/GlCkFPNie1e7sq+XBP5OcM3oVFeXh533XUXX/va17jkkksYNWoUkyZNSrdZKaOzSuK0adNYvnw5f/jDH7jmmmt47LHH+OpXv5owPfHcYh8CzhQRi1KqJVoUSZOlrC/L3uqD5rZGyhyt6TYja2j3htjYEU6bY2ANmpjpHJcW3YMlFBLq6+b2S2aK96+MtCZvfCssgmMYJzRat24dd911FytWrODRRx+lpKSEW265Jd1mpYTYKokA55xzDnfddRd33303v/3tbznzzDNRCRoWjscp+ClGauN7ReR6EcnOEHYNABtcDURyUhOYkwxK9v8r3SZkFe3eEBs9YZQ9PY5BeZ2bkpzsHLKqqrIB0+IXEMWppuSenwdcQmnR8ExoVFVVRVFREZZo7vOKigp8vux9yImXrlUSV65cyYEDB6ioqACM4+D3+xOmL55Bx3eUUu0ichi4A7hcRJ4GfqeUSkwBZ03KUAJN44sp3ngw3aYMCNvBbeSPOY0WT3bmXEgH7Z4QG4FjnGbEn9qpnSLCLP8o3pbmrCuYBLBzx2imTNlPRMWXQGus7w3G249jT8CRNJtCo13DMsvnGWecwcsvv8zVV19NQUEBmzZt4v7770+3WUmls0riwoULOeWUU+jo6ODyyy/nwQcf5IYbbmD27Nls3ryZ3//+90iCTop4nILHxcjoUYmRQ6Az1PN24IqEWKFJKVsr4cSN6bZi4Ixo2kiLvf9paYczbZ4Qm0SY5Ui9Y+DusDCpbDTbm+OtpZY5eL1Ca9s8cnLei1vmVP7Bw5yZNJsO2wSVZqcg3imEicRsNvOrX/0q5Xo7SUebe6uSmKxqkfEMH4wE7lFKzVNKPaKU8mHM1ZmSFIs0SeefhYcJF2RvljTXjpVYdUdBv2ntCLLJF0nLUML4hiJc9uwcttqz243JNC7u7cv97zPd3v2NXKPJdOJxCi5QSr0JICJzowGHAaVU8lxhTVIJmSJsmleYbjMGjIRClFia0m1GVtLpGERcqfWqLGFhVpYWTALYu2dSv1IgL4n8TVcs0GQl8TgFt0bTHN8E/Ar4ZXJN0qSCl8trCOdl8fTEQ+vTbULW0toR5IN6L235dlKZxqq0ycnIvE8VP80KWlpM+P3z4t6+OLCReQ7tuGqyj3icgtVKqfeBM4ElwP7kmqRJBQFThC3zi9NtxoCx79uAw559mRkzhUgENlR1sNduSelwwvT2Csym9OVOGAw7thdgNsXv1JwUfBFzSt0ujWbwxOMUjBeRbwLromWOs3NgUPMpXi4/TCQ3O6c3iVKUfLq6tqafVDf4WN0axJeXmqQ4Dp+ZabnjUqIr0UQiUF09C+IcGMgN7eJYR11yjdJoEkw8TsHfMYob3SYiZ8Upo8kCvOYQ2+aVpNuMAZO/b1W6TRgSBIIR1lR3UOWyoizJv7zH1OdR5I4/W2AmUVtrIRI5Ju7tFweexSq6t0CTPfQ5JVEp9TzwfPTjHuCvSbVIk1JeqjzMVLcDU0f2JQGx1ewiZ3yEdq/2UxPB3lovdU4zMwvsWNsCSdNjUsJc31jesXQQDGVfhavt20YwY2YekUjf2TWd4UOc5DzIm77RKbAsdTxz8w0J3d/5P70tru3uu+8+qqqqcLvd+P1+brvttoTNz++LdLQ5Eolw9tlnc9xxxxEIBNi1axePPPIIP/7xj3G5XOTk5LB+/Xruv/9+ysvLE2KXvpsOc7ymEDvnZWfwF0BxIDuTMGUqHd4wHx7qoD7XhjIl72br9JqZ68jOvPXBoNDYGH8K5IWBP+M06d6CwbJu3Toee+wx7r77bm6++WZ27NjBX/7yl3SblXQWL17MsmXLWL58OR6Ph+eeew63282tt97KDTfcwLx587j11lsTpk87BRpeGlWLcmVnoZW83SvTbcIQRNh2yMMWBeEkTl0sa3QyMT87n6AP7HcgEp9TYws3scS2K8kWDX127NjB6NGfnC8TJkzgjTfeSKNFycdkMnHjjTcCEAqFOHjwIFOnTmX58uVHtolEIuTkJC7vjHYKNLSbg+yaNyLdZgwIS1MNBa7kdXUPZ5ragnxQ56U1iVMXJzeUUODKT9Lek8vuXeMRia8K5Fzfn8k1ZV+a50xi0aJFbNmyBZ/Ph1KK1atXHymjPNR59dVXOeusszjrrLNYuHDhkfXNzc289tprXHvttQnT1aNTICL/JSJviUhxzLq/iEhFwrRrMoa/jqpDObKzzG1Rx950mzBkUQo2VnWwy2YmkoSpi+aIMN8/Fos5nozrmUV7u+Dzxpf61qw8nGr7OMkWDW3GjRvHgw8+yM9+9jMeeOABZs6cyZgxY9JtVko4/fTTeeWVV9izZw+//vWvAWhpaeH73/8+jzzyCEVFiSs61ltPwSnAV5VSDTHrrgNuTph2TcbQYgmwd152+nu5O/41LAvEpJLDjX5WtwTx5id+mMnptTDXlZ3xBTt25GIyxRfgNdP7F0osqa07MdQoKiri1ltv5YorrqC5uZkLL7ywb6EsZvPmzaxYseLI5/Hjx7N7927q6+u5/PLLueuuuxg/fjzPPvtswnT25p5/rJQ6aiK4UmpbtFqiZgjy4pg6fvCRFfFnV0S4ydNCsctLfYdOoZFMgqEIH1V1MLbMSaU3SCJn2o1ocDG+tJI9LVWJ22kKUEqorppJecVh6GOQRQhymnkNT4eOTY1xQ5Af/OAHfOYzn8Fut/OlL32J6dOnp9ukpGK323n44YdZu3YtwWCQLVu28Itf/IIvfOELhEKhI05Rbm4uX/7ylxOiszenoKc5aokr3KzJKJotfg7MqWTMh9mXtLKwaRv1tvgjwjUDZ1+tl5xKNwUtib0VTG0sozG3lRZPW0L3m2zq6syUjTgGk2lDn9tO8q6g0j6PqmB2V/SKdwphonn77bfTohfS0+aJEyfy3HPPfWr9Rx99lDSdvQ0fFIvIyNgV0XiC7IwK0sTFi+MaUNbsG99173gfc3Zmz81KPq7qIOxO7B+bOSzMD47HkoVpkLdvG4HJlNf3hqI4zfRu8g3SaAZIb07BXcBfRORpEXlARJ4BXgbuSY1pmnTQYPVRNXdk3xtmGBL0U2ofHpHImcJWTyjhuQxcHRZmu7MvviAYFJoa58S17Wjfm0yzdyTZIo1mYPToFCilaoCTgKeBKuAvwAnR9ZohzF/HN6Es2ddbUHB4Y7pNGFY0twVpzEn8jJWKBjdj87PPMd2/34nIxLi2/ULoaWw6/bEmA+ltSmIJcAswAbhXKfWUUsqbMss0aeOw1UPNnOy7KTt2r8GWnbMqs5at1e2EkuAYTGscQZ4zcQlZUoWRu6DvYZXc0F4+b9+eAos0mv7R2/DBbzGCDScD16fGHE2m8NKEJpQ5u3JbiVKUmurTbcYwQ9jSFkSZEzuMYAkL88ITsq7Mcnu7CZ8vvtwFs71PM8qqE29pMove7vo7lFI3KaUuA3JTZZAmMzhk81B7TGW6zeg3+QeTF5Wr6Z7WjiD1zsRH0+e0WzgmJ77u+Exix/Y8TKa+M4SaCLGUv8ZZiFmjSQ29DRzHDhUciYoRkSuUUvcnzyRNprBiUiv/scFkFJLPEuwHt+Aa9Xk8Pn2rTSXbazwUVLgSXl2xsj6HhtIKDrQcSuh+k4lSwqHqmYwor6Wv3AUlgXWc7Dyet3zZNVxX92Df0y/7Q+l3Zve5TU1NDTfeeCPr169n1SqjbLrP5+Oaa66hsrKSHTt2cP311zNlypSE2tZJOtoMsG3bNv74xz/idDp56623uOmmmygrK+NnP/sZkyZNYu/evdxzzz0Jq3/QW0/BZSLyoYh8GPN+FXB1QjRrMp4D9nbqjsmumxVASbg63SYMSz5uDqAsiR9ymtE4ghyHO+H7TSa1tRZUZFZc2x7vf5wis8502Bfvvvsu5557Lkp94mjdf//9jBkzhhtuuIErr7ySSy+9NI0WJp5wOMxVV13FsmXLuO6663j44YcZP3483/3ud7nsssu44YYbmDVrFnfccUfCdPZ2Bb8GXBtdLoi+XgO8mjDtmozn5cntkMQSuskgb88H6TZhWNLhDXE4CfURLGET89UETKbsinHZvr0ck6nvkVdLpIOzLOlLypMtfOUrXyE39+jjuWLFChYvXgzAMcccw/r164dUkaRVq1ahlOJ//ud/uO2223jppZcoKCjgzTffZNGiRQCceOKJR6VCHiy9DR/8SClV13WliOiqHsOIvfY2GmZWUrzxYLpNiRtr/QHypoRo9WTftMpsZ9dhL0Uj3dhaE5vtMLfNyqySCWxo3ZnQ/SaTQEBobppHXn7ff/ijfW8y3zmXj3yFKbBs6FBbW3uUo5CXl0dtbS15eXEkksoC9u3bx8qVK/njH/9Ifn4+F110EQ0NDTidTiRa8KWzzYmiN9f79B7Wfz5h2jVZwd+meMi2ikPFvuxL1TxU2NTgQ1kT/1Q/uj6PyrzsKvG9b58Dk0yIa9vPBp7CZdK5C/pDWVkZbW2fpMVubW2lrKwsjRYllry8PKZNm0Z+vpFI+KSTTmLTpk14vd4jwyiJbnNvV+4dnTEFMcsq4M6EaddkBbscLTRNz64Kirk73ss2P2bI4PWHqbYmZyrhrOaRuO2upOw7WezePSGu3AXO8GG+aFubAouGDkuXLmXlypUAbNy4kTlz5gyZXgKA4447joaGBsJhI+Zk3759zJw5k1NOOeVIsOV7773H0qVLE6azt/7V14BHAQEuB34ZfX9RXzsVI63XcuAjYBTQoJS6RUSKgNuB3Rj5D36slDoclbkWyAMKgdeUUi8OsE2aJPDKND/f2CKgsuNJxtzWSKHLT2NH4kv9avpmb62XkpFu7AkeRrCEhPlM4D3ZTERlx6yYtjYTPt887PYP+9x2mucFJjmmszOgK3525a233uLxxx/n0KFDLF++nKuvvpof/vCHXHPNNSxfvpydO3fy8MMPp9vMhFJUVMQdd9zBFVdcQWlpKXV1dSxbtowLLriAW265hddee439+/dz7733Jkxnb07BNUqpBgAROVcp9Vb0fTzzMoqAPymlXojKbBaRFcB/An9XSj0jImcDdwPfFJHjgFOUUmeK4VJvFpG3lVLNg2ibJoFsdzbTMrWC/K3ZE9lf1LqTRvPMdJsxbNlY72NBjgUJJDayPq/NxuySSaxrzZ6MgDu25zNnThnhSB9jv6L4YuQZfiMXE1KZ29UV73S6RLJkyRKWLFnyqfW/+tWvUqI/HW0GOO+88zjvvPOOWjdu3DgeeeSRpOjrrfZBQw/rG/vaqVJqVadDEKOnA1gKrIyuey/6GeCszvVKqSCwBTi5Lz2a1PLa9OzKvube8S+yLGB9SOEPhDmYpKyYlfU5TMgflZR9JwOlhOrqWRBHqqK84C4+Z9+dfKM0mm7orfbBMhFxiogLsHS+F5Ef90eBiJwHvKqU2gqUAZ1RIa1AoYhYuqzv/O5TkRMi8h0RWS0iq+vqPjUxQpNkNruaaJ2SPbEFJp+HEqeuRpdO9td58eYnZwhnan0pJTlFSdl3MuhP7oL53qeosASTbJFG82l6c+NvAtqjy+Ux738W785F5BTgFODK6KpaPkmZnAc0KaVCXdZ3fvepfjal1INKqYVKqYWlpaXxmqFJIG/MCKXbhH5RWL853SYMezbVelFJyF9gUsLc9jE4bY6E7ztZ7NhRjsnUd+Y5IchZppd1CmRNyunNKbhOKWVWSpmii1kpZcJIYNQnIrIUY1rjD4FyEVkMrAAWRzc5MfoZ4K+d66M9BzMAnc0jA9ngbqR9YvZMC3Pu+hBr4tPya/pBIBhhn0gfCX8Hhj1gYpFMxpwl40R+v9DcPC+ubcv8azjBoSvVa1JLbzEFd/Ww/r6+dioiC4CngeOBN4EXgKnAj4HPi8iNwL8RdTCUUh8Ab4rIz4H/Aa7SQYaZy99nZccMBAAJhSixNKXbjGFPVb0PT5KGEXLbrMxxT07KvpPBvr1OTKbxcW17ov8JCszZMctCMzRISso3pdQaoKc+sv/sQaZbJ0STeazPaeDkmZUUfVyVblPiouDQeg4VfDbdZgx7Nh32sKjAhsmX+Dz/FQ1uJpWOZmfLgYTvOxns3TORsWP3o+j9WFgjrSy1vcuTYR13rUkNOg+sZkA8O6ONb2+3IMHMjzGw79uAY8QSfH49QptOQiHFnghMIJ4Y/P4zub6U1kIPte3dTpzKKFpaTARDc7FY1vS57Tjf35njmMt6f+Yk5Xn00UcTur9LLrmkz226q5J4xx13UFNTQ3l5OWvWrOGWW25h2rRpCbWtk3S0GbqvknjssccC8O1vf5t169axevXqhNmlnQLNgKi2dbB7USUT/5X56YRFKUqo5SDZEwsxVKlp9DOi0k1OS2KTGgGYFMxtG817Di8dfk/C959otm8rYtYx+UQiLX1ue1rwSbaZvosvMnwd284qievWrTuyrr29nXvvvRcR4emnn+baa6/lpZdeSqOViaWzSuJLL72EyWTi4osvxmIx/rafeOIJ3O7EVw/tMzpHRC6PvtoSrl2T1Tw75jDhgsTU8E42+ftWpdsETZRNNR7C7uREf1qDJhZEJmI2JSfNciIJh4XGxjlxbesMH+IM28YkW5TZdFcl8Wc/+9mRwkCRSIScnOy4H8VLd1USS0pK2LJlC5s3b/5UUqNE0FueghtF5AQ+KYz0p4Rr12Q1XnOID48rSLcZcWGr2UWOUwdsZQLhsGJdc4CIIzkdlbkdVua5siPw8MB+ByaZGNe2Mz3PMsHmS7JF2UkgEOCxxx5j+fLl6TYloXRWSbzkkku44YYbePvtt/nNb37DHXfcwU033ZQUnb31FOwEvgksEZG/AONFZHpSrNBkLa+VHMI7NjtyRhQHsqf881DH5w+z2RtOSjVFgBGNLqbkj03KvhPNnj3jMWZi94Eovhh5DnNSJndmL4FAgO9973vceuutTJwYn4OVLXRXJXHZsmUUFhZy77338tRTT1FTU8Ptt9+esPLJvV2RDRhTBt8CroiuWyYiw7sPS/Mp/jpfZUVp5bzdK/veSJMyWjqC7FQCpuScO5NqiyjPzXyHtbXVRCAwN65tC4JbOcW5L8kWZQ9er5fLLruMq666igULFvDss8+m26SE0l2VxKuuuor77ruP66+/ngsuuIDy8nKuv/76hJVP7s0pOAMjx8AC4AKgCbhQKXVMQjRrhgybXU3Uzq5Mtxl9YmmqocClU8dmErXNfg46LEl59hURZreMIseR+GCsRLNjeyEmU2Fc2y7yPIlZJX5aZ6bTtUqi1+vlwgsv5L333uPyyy/ns5/9LLfffnu6zUwosVUSb7nlFurq6rjySiNB8OrVq48cj0S2u8c+K6XU1QAi8iZGqeMJwFoROaSUOiNhFmiGBP83tZnvb7Uh/swumlTUsZtmmZpuMzQx7Kv14qhwUdKW+HPHGhIWhibyrnkzoXDmTp8Nh4WG+jkUFv2zz21N+BFJ7xBCvNPpEkl3VRKfe+65lOlPR5uh+yqJAAsXLkxKqeh4BvReUUr9CVirlJoD/HvCrdBkPfVWL9uOLU+3GX2Su2NlNox0DDu2HfLQlqSMh26PhXnOzA88PHjQhsikdJuhGeb06RQope6Ivr0h+vlQUi3SZC3PjjpEqDhzEqx0h8nTQrHLm24zNN2woaodf5Icg7JGJ9Py40stnE727B6PiC7WoUkfcYf+RksfazQ9EjJFePe43L43TDNFjfpUzkyEjw51EMpJTkqUCbUFjMxLTDBWsmhrE/z++AomaTTJIDtKi2myhrcKa+iYmNnDCO4tbzPKfjjdZmi6IRKBdY1+Is7E5zAQEY5pGkmeM7MT3OzYXoDJVJxuMzTDFO0UaBLOC3MCkOGlbEs/+BPjTXvSbYamG/yBMBs7Qihb4rMSWsImFgQnYrdmboLWSATqamen2wzNMCWz79yarGSHs4XqeZk/RbHgoxeZHNqoAw8zkHZPiO1hhTIn/sdxecwczzTs1uTELySC6morgp4lo0k9uiCSJin836QGfrDFjngSX/gmkeRs+gdTJrezM28x4eE39TujqW8J4Cx1MNoXItEz8HI6LCx2TeV92zZ8gcw8R3ftGs3ESXtQKvOm+a756IKE7m/B/Kf63Ka7KomdPPnkk1x00UW0tbUlrf5BOtoM3VdJbGpq4rHHHmP27Nm8//773HnnnUyZMiUhdumeAk1SaLb42XRsZgd1deLa8SFTa1/HqoO+M44DdT7q3Mnp6nd7LCyOTMVhcyRl/4Olo8OEz6eDDjvprJKo1NEeYmdxoKFIZ5XEZcuWcd111/Hwww8zfvx4rrjiCq699lquv/56lixZwl133ZUwndop0CSNv1QcIjAivixt6cZ+YDNT9z2Pw67zymcaO2o8tCZpqqLLY+GE8BScGeoY7NyRj9mU+amaU0F3VRI9Hg933nknP/3pT9NkVXLpqUriiBEjqKurA6Curo4FCxYkTKcePtAkjYhJ8Y9j7ZyRJeXNrbX7meJ7it0zv067N/NL7w4nNlZ1ML/SjbMl8V39Tq+Fxc6pvG/fjsefWTksIhGoOTyL0tI3021KRvLf//3f/OQnP8Fmy9zA0cHQWSXxj3/8I/n5+Vx00UXYbDYeeOABLr/8cl599VXWrFnDpZdemjCduqdAk1Q+yKujderIdJsRN+bWeias+z0Frswbxx3urK3uIJibnJu/02vm+NAU3HZXUvY/GGoOWQFdoLYrBw4coKmpiWeeeeZI7v97772X1atXp9myxNFdlcTXXnuNpUuX8qc//Yl77rmHq6++mm984xsJ06mdAk3SefYYD8qcPaea2dvBuA8fotTlSbcpmhiUgrV1PiKu5AR/OL1mjg9OJseReY7Brp2jEMnc2RLpYPTo0Tz66KNcf/31XH/99QBcddVVLFy4MM2WJY7uqiROnTqVxsZGSkuNYaWKigp8Pl/CdGbPnVqTtey3t3Fgwah0m9EvJBSkcuVDjHQ2ptsUTQzBUIQNbYGk5DAAcPjMHB+YknGVFT0eweudn24z0kp3VRLBGFNfvnw5AHfeeSdVVVXpNDOhdFcl8Uc/+hH33Xcfl112Gbfddht33303v/71rxOmU7pGcmYLCxcuVAPtJlpVs4rfrP9Ngi3S9EZO2MqVK0yY2rLv6bth0VfYH8z8vAvDidICO5MjESSSnPuX3x7mA8cu2rztSdn/QBCB2XPWE4kcZt7cRzGZBjaUIiJrlFL9epxes2aNSmQwmya9rFmzhptvvvnXwNoXX3zxodjvdE+BJiW0m4OsPS47U7cWr/ozE9U20EmOMoa6Zj81SUiF3Indb+Y476SMSomsFNQcmok+ETXJRDsFmpSxoqwaf2V2OgZ5619hind1pmdvHlbsPuxN2lRFAHvAxHGeSeS7MqfI1+HDFlAz0m2GZgijb3GalKEEXlmYvVP93FvfY2rT21j0RN6MYWNVO4G85E1HswVNHNcxkQJX5pQE37lzJErp3gJNctBOgSalrMtpoHFW9o7PO/asZWrVCp39MGMQ1tX6klJVsRNr0MSxHRMocOUnTUd/8HpFOwWapKGdAk3KeWZGK5G8zIru7g+2QzuZUrVC9xhkCMFQhI89YZQlebcza9DEse0TKHIXJE2HRpMJaKdAk3IOWz28eKoblcX/qrbqnUw5/Lp2DDKE1o4ge80mkvkAbQ0Ji9rGU6wdA80QRt/SNGlhvbuBkaeO5NjXDqTblAFjP7CZKSYz20pO1RUWM4DqBh85FS5K25KXjdISEha2jmN9wUFq2uqTpifT+be1OxO6v+fmTepzm+6qJHbWBQDYu3cvzc3NPPLIIwm1rZN0tHnXrl3ceOONzJ8/n4MHD1JcXMyyZcsIBALcc889uN1uNm/eTHFxMbfeeiuRSIQf//jH5OTksG/fPi699FKOP/74ftmlnQJN2vhbaTXlx41hzAf7023KgLHv28hks4XtBScTiaTbGs32Qx7clW5cSaiR0IklbGJ+w2i2l7rY2ZK952620Vklcd26dUfWPfHEExQUFHDxxRcDsGHDhnSZlxQaGxv5+te/zrnnngvAjBkzWLp0KS+//DJLlizh5JNPBj5p9zPPPENrayu33347jY2NHH/88WzZsgWzOf4Abz18oEkrj06som1yRbrNGBTO3WuZ3LYS0VdTRrCuuoNQbnIjQQVhal0J8/KmYtI/fErorkrik08+SWNjI7/4xS+OPCEPJRYtWnTEIQCIRCK43W6eeuop9uzZw/33389PfvITysvLAVixYgWLFy8GjGyIDoeDjz/+uF869dmsSStK4MEFTQTLsnuc1rXjQ6Z0rEJ0UHjaUQrWNwaIOJI//XVkvZvF9hnYrbouQTrYt28fra2t/OAHP+CSSy7h+ZURJAAAIABJREFUjDPOOFInYKjx/PPPc/rppzNt2jT27t2LiHDFFVewZMkSzj//fABqa2uPcpzy8vKora3tl55h6RTo+3Zm0W4O8sTJoFzZfWN1bfsXk31r9QmWAfj8YbYHFMqc/B+joNXGiZFpGZXkaLiQl5fHcccdB8CUKVNobW3lwIHsjVPqiTfffJM333yT++67Dzi63SeddBLvvPMO4XCYsrIy2trajsi1trZSVlbWL13D0imY4w8yxpbdT6ZDjf32Nl49rZBsTxno3vI2k4Mb022GBmhoDXDQZiYV1V2cXjOL2yYxMq9/N2DN4DjttNPYvXs3YPwBhsPhI13pQ4UVK1bw6quv8sADD1BTU8PKlSuPave+ffuYOHEiZrOZpUuXsnLlSsCIR/D5fMycObNf+pJyBxaRchF5SERWxaxziMgvReQGEXlERKbEfHeRiNwjIneKyGXJsCkWayTMf9XV4jZl95PpUOODvDo2LsmuaordkbPpH0xUW9JthgbYX+ejJS8117k5LMytq2RqwbiU6BtudFcl8brrrmPdunX8/Oc/58orr+Sxxx7D4XCk29SEsWbNGr72ta/x/vvvc8opp3Duueeybds27rrrLp599lluu+02br31Vp544gkAzj//fHJzc7n55pu59tpr+cMf/tCvIENI3uyDk4AXgLkx664A9iul7hSRY4CHgc+IyCjgGmCeUkqJyCoR+YdSakeSbAOgxNPMd1353GcVIil5ltDEw3MjqyibO5oR67K7CzBv/WtMmGdht5qcblOGPR9Xd7Cw0oW9JXlTFTsRESbVFpFb5GCtZzvhITolJZ7pdIlmyZIlLFmy5Kh1TqeT3/3udynRn442L1iwgPb27it1PvTQQ59aZzKZuOOOOwalMyk9BUqpPwNtXVYvBVZGv98IzBGRPOB0YI36pIbzSuCLybCrKzPr93GeOTsL9AxlHppeg2ds9nfD5q99mXGmPek2QwOsq/ESdqcuN/WIRhcnWGfgsA2dp1bN8CCVA7hlHO0otEbX9bT+U4jId0RktYisrqurS4hRSw9uZr49+/+AhhIhU4SHj28nXJj9gVuFH73IGGt293oMBUJhxcbWAMqWuoJceW02TgpNo9CdGTUTNJp4SKVTUAvE3uXzout6Wv8plFIPKqUWKqUWlpaWJsywSw/uoMKaOVXQNNBo8fN/p9hQ9uyvPFS86jlG2w6l24xhT4c3zM4IKFPqpofYfSaOa53AqPyhFfymGbqk0ilYASwGiMYUrFdKtQKvAgtEjszwXgz8LYV24Qz5+X+NzThM2f8HNJTY5mzm7VPLGAqT/0s+fIZKe//mC2sST22zn8Mua0qjiMxhYU7dSKbnj0+h1oSjIkM0PmK4EYlE+GS0/tMka/bBEuCbQIWI3CgiTuABYKyI3AhcDVwKoJQ6CNwN3Cci9wAPJTvIsDvK2+v5dsihp5hnGP8sqmHnCWPSbUZCKPvgj4x0NqTbjGHPrhoPe+0WlCO1Wd4n1BWyKGc6FlPqhjAShclk2lpTUxPWjkF2E4lEOHToUMTn8/VYuCMpV4VS6i3grW6+uryH7Z8AnkiGLf1h/uFdnDnmGFYED6fbFE0MT447yA+aKincXJVuUwZN2ftPEjn+Ymq82Zsnw+2MYJEwLZ7s7VmrbvBRaxZmlLvITWKdhK6UNTo5wT2Dj2y7afd1pEzvYIlEIl+orq5+s7q6epIMgZ674YpSCp/P1/j4448/DhQDn/qz0wWRuvBv+zewd9xMPvYP3wpomcj/zq7nh83F2Kuz+0lblKJi5WMUjZlB08j51IeLCQbTbVV8iAlGmw5Q9OELSDhMOL+UtgnH0+AYTas3+xyEUFixoaqD0gIbk2xmTJ7U/BC5HVZOMk9hR1E9u1qyIwh1wYIFB88555wpwJeAc4ChmUt4+JAP7ALe7PqF9Da2kMksXLhQrV69emDCe96Bt3qey9lhdXJzeQX1oe7nh2rSQ0XAxbdfCWNq86TblIShzGa8k46jsXgGDT53xlZazHcFGb3rb1gPdz/FMlRYTtv4Y2m0j6bVm33PGiIwY6Sb/LYAEkndPbE538+6yB46/P07py+66CIsloEdZxFZo5RaOBDZc845R4Byjg4O12QfAaD6xRdf/FTyDu0U9MD+/BH83G0moEID06FJCnPaizl3RQMSGnoPKmGnm44pJ9Lgnkizx5ZucwAwm2FsZCd5615G4rxXhIrKaRt/HA22UbRlmYNQkGtlqtuCpT113Tchs2JHUR27Ww7GLZMup0Az9MmuKzaFjGk5zMWuKTxEc7pN0cSwPqeBilMrOPbNGiQ4tBw2s7eDvPWvkYfxx9o64QTqLZV0+NJTD6LI7aNyywtYGmv6JWdprKGw8QUKgVBxJa3jFtFoq8wKB6G5LcgHbQGmVrgp9gSRcPIfmixhYXpdGeUF+awL78bj9yZdp0bTE5l/laaREw5tZ8/YWbwR0FPJMolXSg+x+jwnZ+8rYvTaQ0ggSwbl+4GlsYaixucoAgKV02gevYC6cAmpaKrVCmN9m8h9741B78vSUEVRQxVFQKh4VIyDkMkR+MK2Qx5ynBamF9qwtSY/PTJAYbOdz5insr2ojj0t2R9Uq8lOtFPQB1/bv5n9Y6ayI5DdAW5DjXqrl99PqqJonJ2z91Uwdm0N4k/NzTvV2Kq2Ula1lVKTCe/EhTSVHkNjIIdQEjpKylztlG98HnNbY8L3bWk4SFHDQYqAYPkEmsYtpjZckrGBlu3eEKu8ISaMcFEeCCHB5Ad8WMImZtSNMHoNQrvxBnxJ16nRxKKdgj6wqAjfP3yAm0tKaA4PnQC3oUKjxc9jE6soGGvnnAPljPuoBvENTedAIhFcOz7EteNDRooQGDmVjvJptNlH0Ox3EBlEmIXdBuNaVuFa96/EGdwL1prdlNXsptRiMeIoCqfT2JGZVUt3H/ZQbTczq8SekqJKAEXNDk62TGdbYS17da+BJoVopyAO8n3tfL+jgDscJsJkaHj4MKfZ4ucP46vIHWPjnANjmLj2MOJJ3fzzVCNKYa/air1qK0XAGIsF/6iZdJROptVaSovPhorzVK1wNlO67s+YvamfNy+hEDmb3yKHt6gsKqdl4knUmkbi82fWXHifP8zqKg9jSp2MikQQf/IDXS0hYWbdCMoL81kX3I1P9xpoUoB2CuJkUtNBvl45nScjehghk2kzB3hyXBU5o62cfXAMk9bWYuoY+jdTCYVw7F2PY+96ioGIzYF/9CzaSybRYiqmzWeha25fp0Mx7vA7ONatTYvNXbE01lDc+GeKRPBOXEhj2Rzqfe64nZtUsL/OyyGLiRkjnLhb/UgKJm8VN3X2GhxmX0t18hVqhjXaKegHp1VtYc+4WfzLrwMPM512c5A/jq3COdrCOVVjmfJRLab24RPVbQr4cO5ajXPXakoxpjv6xsyho3A8LVJEQaSOkjXPI8HM600RpXDtXIVr5yoq3AW0TT2ZWvtYOrzpmYXRlWAowvqqDvJzrEzJtWJrS/6QgjUkzKorp7yogPWBXUnXpxm+6DwF/SRosnDr6AnsD+ipitmEM2xh6aEypq9txNSaPellNZ/gHzODxspF1AUKCGdQmoqRxQ7GmiVlGRGD1gjl35yNyTIwJ0nnKdD0hu4p6CfWSIhrDh1kffEotthtbA616wDELMBrDvHnUdXYR5pZWjOGWSuHbkDiUMW+fzMV+zczwuagcc7ZHAyPzIihheoGH9UoJle4KfUlf5aCNWjShds0SUM7BQMgJ+DhxEPbOTH6uSanmC15pWy1WdgSaqU9PPTHsLMVvynMcyOrWHVWDhd8kI/jQF26TdL0E1PAR8mq/yO/bAwHJy3NkOyPwo5DHvZaTEwb4SQ3xemSNZpEoZ2CBFDe3kB5ewOnAArFwbwRbM4rYatZ2BZqxhfJ0InYw5gD9nbu/oxw4e4xjP/gAGTpMNpwxlq7n/G1v6HtmM+xzzEzI/IdBEMRNlZ1kOe2MiXfhj1FiY80mkShnYIEIwijW2sZ3VrL6UBEYG/+SDbnFrLVrNgZaNb1FDKEsCj+MLGKRaVlnP5WO2Yda5CV5G78OzNcqzg850sZU5K6tSPI6o4g5UV2xllMmFMUb6DRDBbtFCQZk4IJzdVMaK7mLCAoZnYVVbLFnccWCbEn0KxzH6SZVXn17PiinX9fN5K8bXrKVzZi8rRQsfIxCsfNYX/FyRkzU6Gm0U8NiknlbsoCYSSQQRGSGk03aKcgxVhVmGkN+5nWAOcBPrON7UUj2erMYTMBDgSbu04n16SAZouf+xYe5rzKMRzzdjWSjBzCmqTj2LueyQc/pmnu2RyIjMmQUtTCzhoj3mD6CCd5bQHQ8QaaDEU7BWnGEQ4wu24vs6OfO6xOthaNZKvDxWbl5VCwNa32DTeer6ji43MK+PK7YWy1etppNiKhEEWrnyevuJKqaWfR2OFIt0kAhKLxBjlOC+OL7OQEwpi82vnUZBbaKcgw3EEvCw7vYkH0c4sjhy0FI9lit7El4qE+1J5W+4YD253N3HuamW9tG03FRwfSbY5mgFgaqhj73u8onn4y+3LnEciQmL92b4iNVYYzkJ9jZWSejbxIBHN7UE811KQd7RRkOPm+do6v2c7x0c91rgK25o+g3mqlXaBdFG0qQrsK0R4J0h7xE1J63HKw+E1hHpxezZIRIzn5rUZMHj3NNFvJ2fI205xrqJ97HtXe4nSbcxQt7UFa2o0gRIfdzKhCO4UmsLYH9ZRGTVrQTkGWUeppptTTe7e2z2yl3e6mzeag3eKgzWql3WSl3WyiTaBdoFEFqQ97adM5FXrlraLDbD3LxcWr8nHtOZxuczQDxOztYMTKJygYNZ0Do0+jzWtOt0mfwucPs7PGSIRmsQiVRQ6KLSYcniASyojgCM0wQDsFQxBHOIjD00xJHIkWfWYb9e4C6h051Nsc1JpN1IuiPhKgLuTBr/RUqsNWD3cv9vCNyrFM/tcBMiR6TTMA7Ae3MLF6G57Ji2konkWD1/GpQlGZQCik2FfrZV/0c0WRnTKnBZc/hMmnewI1yUM7BcMcRzjAqNZaRrV2X+Spzeamzp1Pg91NndVGndlEHWG2B5qG1TCFEnhq7EHmFJdw9ttezE1t6TZJM0AkEsG97T3cvEdlfinNkz9DnWUUXl/mjugfavRzCKN4VXGejRNQZF5fh2YooJ0CTa/kBjrIDXQwocv6DquTlSPG87YpyMFgS1psSwfrcxrYdbqVzzSOZlJ1hILdDTreIIsxt9RRvPo5ikTwjZ9LU/k86ny5Gd0Z1NAaAB2SqEkS2inQDAh30MvnDm7mc8DuwpG8k1/MB8HGYZHSud0c5G+l1VAKMhuO6Shldr2Tyn0eHFUNOmVyFiJK4dy9FufutZQ7c2idejL1zgkZGXug0SQT7RRoBs2EpmomNFXzDZOFVSMm8o7NxPZAQ7rNSglKYENOIxtygHFQFHKyqKmIydVQuLcBU7s33SZq+onJ207BupcpAPyVU2gafSx1oWJ0PivNcEA7BZqEYYuEOPHQNk4EanJKeLuonH9FWmkdRjMcGi1+Xi09xKvRXoSZnlLm1DkZtd+Lo6peZ7LLMuxV2ymv2s4Iq52OqSdSlzc1Q6oyajTJQTsFmqRQ3l7P+e31fFmEDaUTeNvpYGOgnkgmhnonCSWwyd3IJjcwDgpCThY1FzLlkJDT6MPiDWDy+DH5AnrIIcORoJ+cTf8gh38QKh5F27j5tNoraPE7CA+feFvNMEA7BZqkYlaKebW7mAc0O3J5t3QM74qP2uDwi95vtvh5vaSG10uOXm9WZgpCdgrDdgqCVvKCFnIDZlx+cPnB6Ytg84WxeoJYvH7MHX7En8b0fCLD2omxNByksOEghYAymwmMmkF76WRabSNo9dkyOkhRo+kL7RRoUkaBr42zDnzMWUCDK589uaXscTjZIyH2BluHRZBid4RF0WD10WD1QZxp+p1hO6UhJ2UBO0V+K/leE3lecHWEcXQEsbV5Mbd6+13YSdlthPJcBHJs+HJstLtMtDmhyRGmwR6kzuaj1uKlIGxnRnse45otlNQFcVc3YeoYPsNEnUg4jH3fRuz7NlIMKIsV39jZdBRPotVSQqvXMpz9J00Wop0CTVoo9rRQ7GlhYfSzQnE4p5TduUXssdnZS5ADwVYCSkd3dYfXHGK/uY399jbI7Xm7gpCL0oCD0qCdQp+ZfJ+ZHE+EiEloc0KLM0KDLUi9PcBhqwePOQT03YtTb/LydqGXtwuB8ca60f58prXlMqrZRMlhH85Dzent0UgDEgri3LUG5641lAARhwvf2Nm0F0yg1VSkZzNoMh7tFGgyAkEob6+nvL2eE6LrwiJU5ZWxx13IXquVPfg5GGglgu6fjZdmi59mi58dAPnJ1XXA3s4BezuUAJNAFEzwFzG1zU1lo1B02Iv9UNOwKktt8nlwbXsfF+9TBkRc+XjHzsabNxK/OQc/DrxBM4GgzjugyQy0U6DJWMxKMablMGNaDrMkui5osrA/fwS1dhfNVhtNJqFFoFGFaIkEaAp5CGunISNQArscLexytEApMBUsERNTfCUUBqwD3q8gOENCgc9Mrgfc3jCOtiC2dh/mVg8SzFynw+Rpwb3lHdxd1kdsDsJFIwnmjSDgLiZgz8dvduGL2PEFzXo6pCZlZJRTICKfA/4NqAWUUurmNJukyTCskRATm6qY2Ms2bTY3zQ43TXYXzVYHzRYLTSahWUVoIkhz2Edb2DeM5kFkDiFThM2uJnAlT0deyEFZyEWpz0ZhwEq+V8j1KlwdIeztQaytXsztnoyaHmoK+DDV7MZas7vbQxNx5RMqrCCYV0bAXQTMSbWJmmFCxjgFIuICfgvMVEr5ReRZETlNKfVGonV1iIuAu2vi3vgRAVERTCqEWYUwRUKYVAiJvhcVQiIhnYg0TXSmZh7dyzZhEZodubTYc2iyO2m22Gkym2k2KZpUhGYVoCnsHbbBj9lMqyVIq6WFnb0EbVoiFkYG3Yz0ORnhtVLQAXltYVwtfmzNHRmXdMrkacHmacFWtRU3YIosBV39QJMEMsYpABYD+5RS/ujn94ClQMKdgg3hcTzQ9I1E7/ZT2ERhN4WxmyI4TGFspggOiWAzhTFlcUiyCJhFYZMwdlMYq4SxEcYmEawSwiIKGyGshLFIGCshLBLBQhirCmImgilTuvgV5PkgDxjTzdcek4Umq4Mmi4Vmk5lmUbRIhKCEgAgRFQIJowgTUWGUhImoECr6XSS6PqyC0dcwEfTE9nQTMkXYb48GanYTa+GM2Bntz6HC56DEY6awHXLbQjhavFibOoZdAKVm+JBJTkEZR4c9t0bXHUFEvgN8J/qxXUS2DUJfCVCv5bW8ltfyWSf/+B8GIz92wHo1Q55McgpqOXpyVV503RGUUg8CDyZCmYisVkot7HtLLa/ltbyWH1ryGk1PmNJtQAwrgbEiYo9+PhFYkUZ7NBqNRqMZVmRMT4FSyiMi3wN+ISJ1wIZkBBlqNBqNRqPpnoxxCgCUUq8Dr6dI3WCHIbS8ltfyWj5b5TWabhGVxVHwGo1Go9FoEkcmxRRoNBqNRqNJI9op0Gg0Go1GA2inQKPRaDQaTRTtFMSBiAw4n6iIDDrbsYgUp1n/xETsZxD6093+AetPhA3ZfPyj8oNt/6Dy+SZAf7rbn1b9muGFdgr6QERuA/5DRPo9U0NEipRSSkQGfJxF5BbgIhHJG4BsWVT/YJya/wa+Qkx2yXhvMiIyLvqaze0fsP5E2DCY4x/ddlz0dUC/QQa0f8DXX1R+UNdgBrQ/rfo1ww/tFPSCiHwT2A68Arj7c2GJyK3AmyIyUSkVGchNSUQuiep/EnCJSF68NkT17xSRmUqp8EBuCiLyLWAn8AvAKSKjRcQWvcn0+sckIjcBu0XkhCxu/4D1J8KGwRz/qPxNDOI3yID2D/j6i9E/4GswA9qfVv2a4UlG5SnIJESkBHAopf43enHOA3JF5C3gSaVUjxXOo081tcDfgIdF5FKl1C4RMSml4qoEJEZmR4tS6tHon8M8oADYKyI/V0r1VZFlPfAr4GUROVMp9bGImJVS/anGY1ZKPS0iF2HUai2L2vZdpVRfZeTexHA63xCRzyul3s2m9idA/6BtYHDHHwbxG6S7/YO5/qLyg7oGM6D9mXD+aYYhuqegZ8zAGSJyBbAPuAHDa/8sMLEnoegTnAD7MUpBrwZ+LyKTo08r8Xb9uoHzROQ6YA9wDcYNbgxGCuge9UdviG3AfwN/AF4RkWOiTwu2eJSL0V15loj8FKN65bXAL4EI8NVe5EzRJ7KIUmpZ1IY3ROQz0fY749FPmts/UP2JsmGgxz8qm4jfIK3tZ4DXX6d+Bn8Nprv96davGa4opfTSZQFs0dfvAq8Cp8Z89yhwRhz7sERfK4G7gdeALwAL+5CzA87o+y8Da4Cvxnx/R+znXvZjjXn/M2AXcDbGDcXci1wZkBd9vwTYC3w/5vsrgH+PQ7895v01GDeoC4HTMZ4AM7X9CdE/UBsSdfwH+huku/3RbQd9/UW37fc1mO72p1u/XvSiewpiEJEfihHY84KITMLofm0Avici80XEClQDB7qRPUtEKmNWRQCUUlXAzcBh4BGgxxSSInIlcBOwUkROAtZFbbhWRE6OPuF5McaZu8p+U0QWxaw60kWolPpJdD9/Avyqh+5DEfkhxp/HeyJyPsYTyv3AMhFZKiJlQA6wqRvZ/yci58asCkafVlFK3Q38L/A40KiU8mVo+wesPxE2DOb4R+UH9RtkQvsHev1F5Qd1DWZA+9OqX6MBdE9B5wJcCvw7YANuwXhCWwxMAq7HeMq4HZjfjeyFGOOXVwMjY9Z3ppEuAG4ETu5F/wXApdH3VwDvAOcD44DLgH9G9X/qKQc4E9gCLAcWdKM/B/gO8Jle9J8DfC/6/mLg6c72YHRXvwLcBizqRvYE4F3g18BZsfqjiwP4N+CkDG7/gPUnwobBHP9E/AYZ0P4BX3+JuAYzoP1p1a8XvXQuaTcgUxaMsbfYm+mPMJ5IxkQ/VwBlPcgeA/w/4O/RG9jILt+7gNI+9F8N/L+Yz/8BvA/Mi34uBHJ6kJ0KXInxJHhX7E0h+r0DKIj5LN3s43vA3TGfzwaeA06PaYO1B/3jgR9Gb7oPA2d3+d4CuPrQn+72D1h/ImwYzPFPxG+QAe0f8PWXiGswA9qfVv160UvnknYD0r3wiSd9BfBzoDDmu+XAPX1dQMDo6OsJGB799UAuhnfe4428i/5zgAeAY2K+uw54hj7G//hkDHI68BhwJzAlaoMtzuMwC3gIODNm3WUYwU197gOwRm/ct2D8KX0WyCNmXDsT258I/Yn4DQZ7/Af6G6S7/STg+otuO6BrMIPan9bzTy966VyGfUyBUkpF374AfA64Mjp2C/AScChmm544GN3XvzDGBD+LcUP7LyA/Tv0fYtzQLxaRBdF1TwHrVB/jfyo6PU0ptQXjxpKH8cR4ExBvNrQDGOO3S0XkS9F1f4ra1We0tlIqqJQ6hBHpvAPjyedXwIg+5NLa/kToH6wNUQZ1/KO6+/0bpLv9Cbr+YIDXYAa1P93nn0YDfOKlDmskOndZRGYAvwE+wJgGVQC8oZR6v5/7uwTjae0bSqn34thelFJKRMYDPwU8GH8QQeB1pdTKfuo/N6r/v5RS7/RDrgLj6XQC0AE0An8dgP4lUf3LlFJvxbF9WtufaP0DsSEqk5DjH91X3L9Butuf6Osvus9L6OUa7Gxz7Pv+tD9Wvgf9/Wl/Rpx/Gg0MU6eguws65sY0CpiPEeD1vlJqXV+yXb8TkVMBT083sz70FwNjMboB1ymlPo5Xf8w2izEijD/qbbsebHdiPFktALYppbqNdO5jX3OBkFKqpyj5jGh/lz+GuPTHa0tvNvTQ/riPf5zHoNffoJvt+93+PvbXr3Mw3usvjv3EdQ32oj9l7U/X+afR9MawcwrESBMbiPn8qSeGgcj2Q78DCCulgtHPRzKsxaG/R9l+2jAgucHKRuUdQLC7LtE429+tbD/0V2Acw9r+6u9LPk79+UqplkH8doOVnwt83HkOdfkuXmejW/k49X8lKr9lgPp7lI9T/4PAGqXU7waov0f5OPWXYySVGuj516O8RpMIhlWaYzHShX5GRKqBVUqpl6JPFaKiRLfr7kmuV9mY7Xrz3i8Bjgc8IrJeKfVY9OnApJSKdH1q6I9snPr/Qyn1SHdyXbbrrv0Dlo357nvAZ4A9IvKMUmp97Pd9tL9X2Tj1fx84BfCLyG+VUu/GyvSmPx75vmwQYw7+GSLyJaVUdS96kiX/K4yn52u72z6O9vcqH4f+/8B4Cu7a+9b1/B+QfBz6b8UYty8RI+NfJFYujvb3Kh+H/suAzwM+EfmVig4L9OP49yrfl36NJh6GTaChiFyOkczkUcAP3CgiX4Wjgn1iux+tIjJ2sLJd9DsxooLfA64TkWuj+zjqBhD947WKyPT+yHbRP72L/vOAh0TkxRgd3f7+0X3YRGShGMQlG6P/iGzMd9/AGCf9HVCCERndLd20Py7ZPtr/PaAFI/iqHuN4xrZXYj5Huu4jXvnebMBIJtMKPC4ihVE9jm7a3+0xjEe+p99ARO4BfEqpa0VkkYicKiIndurror+79scl31P7o79hm1Lqp8A0ETlPjKf+Tn3dHb+xCZS/EygCvhX97Ub25Nj20P645Htp/9UYSZOuw8gsWCDRdMNxnn9xyfdx/mk0fTIsnAIRyQdmKqUejz7dPYeR3ewSEZkTs92RGypGwhjvYGS7mBEGViqldgPPY6RwvUBEvhy7j+irDaNcblN/ZGP0x8p2sgkjZ/x4EVkBR99Mu9F/Hp9EfsclG6M/VhYxgt7OV0o9o4ygt9eBpdHvRvSg/ytAU39ke2p/9Hc6QSn1pFJqG0Yg1/ki8hsR+UG0Pao7/f2V785jXvXpAAAJnklEQVQG+cSB2o0x7fAtjKx9d2Dk+O/1+PdHvrvfQESOxZjvf3X0j/RkjDwIt4jIhb0d/+jnuOV7OQebgA9E5IsYT/ujgOVi1Dbo7vh1vYYGLB+9Tj6nlPqeUqoRIyPgt0XE3Mv5H9v+uOV7+P1tGKmW31NK7cJw7P4TeF5Eboi1vwf9ccv3cQ/QaPpGZcC8yFQswF+A52I+X46RIeyznf9d0Vc7xg1lVCJkY2R+AqyO+WwFLgGuiEP/YGQ7v4ud//wx8LfoextHJ7U5so/ByHbT/guBUkAwpsj9PLr+Wo7Obd9dGwYsG/Pd16L7KMNIjHM8Rm75Fzk6qUu3+xisfPS7EzGm3Y0D3gZWYgTVTUu2PEbGvHuBr0c/F2BkEOw8lr2ewwOVj1n/fYwsfd+K2ecpGE6OJVnyXY6dHcOJKgWu7eE+kSz5X2LMqrgb+B9gWtT+lzg6N0NS5PWil3iXtBuQ1MYZN8wvRN9PwHjK/ztwKzAZIzXot2K2t2CkFh09GNmYdbld7Pkb8G7M5y9g5LbvvKGZoxf06MHI9qQ/Zr0J+AhYhZEFrzBmfbf6+yMbh/58jFS+FRj52I/rq/39ke1NP4Zj0VlwZxFGrfrc7vaRKPmY32gxxhDQD4AzMOoQ7Ceafa7rMUyUfIztn+doZ+tsjAx4lnjanwD5J4EqosWYgIVReXt311Ci5bvs65fAf3ZZ1+fvPxh54CTg20RTVWOUw/4DnxTASqi8XvQykCXtBiStYUba2Bsx8sE/jNH9B0bp0VEYT3zXcvRTVlF0GbBszOebMf60K2PW2YAV0f1+AyO5ytyY790Yf3oDlu1JP5/8sXTewCcCzcBpMTIWjAxwA5aNQ79Ej9/bGE7WGTEyOd21vz+yfemPvp+BkVP/h8TUEog9homWj66zY/QwLY5+/jHR3qauxzAZ8jHbHRu1/xqOzpPfq/2Dlcfo4XodI33vORiJdeZ1dw0lWj7mHDJFX2didMFb47F/sPIx29yOUQJ6HsY9Zn4y5PWil4EuQzKmQIwAqHKl1HKMiPV64JsicqJSaj/Gn9qjwD+UUls75ZQxXjh9oLJRecSYazwOIzDouyIyMrpNQCm1FKPGewvwFxUzD1sp1YFxYx+QrFKqpSf9Sh0ZcwyJiB0j/elJSqk3OscylVIhjD+eAckqpdrj0K8whgAWAD9VSr0S04b27tofr2w87Y9ufhJwH/BPpdSqrscwGfLRTQR4UCm1Mjru+zul1D9j5ENKqfZkyXex/3bg70qpNfHaP1h5ZWRc/Dzwe4zf+a9KqbUx8o1KqcZkyMecQ53BgW3AWypmamU8v/9A5WO2uR4jDfNXMRIzfZRoeTSaQTAk8xSIEXV7D/AjpdSm6B/Z7RhPEd+KbjNJdZ8YZsCyMftwYAR6hTFq19cAv1ZGCde+bB+wbH/2ISJm1X2ugAHL9nMfC5VSqxMp2899jFVK7Uuh/G+VUt2W/E2RfFf7K3s6p1IhP1j7s11eROxKKX8y5DWawTDknAIRsSqlgiJyF1AH/FkZUfuIyCvAD5URQZ5Q2W72YVZKhcWYzncmsAf4B8a0qm6zlA1GNov0e5RSG2K2j00eNWDZgeofrP2JPoYpkE93+9tVL1kWUyCf7uPfoZTamCx5jWawDBmnQIy5/GUYAWjLMeazX4sRLf9y9PUe4GalVF2iZLvZx0iMErjbYr77/+3dT6hVVRTH8e/KR+HASov+EJgl0iAoQooMSiEH1aAwskkI/YEIJyEiGSGGJkqDCBJBEUkbRIOImoSB0KCahPaETIJExbT8k74QFDJZDdZ58HpqqO/cZ8f7/cCGd6/3d5Y80LvYZ5+951LHuk4GFo7+T20sWeu3cw3z5rucl9pyVawpiNpY5hS1EvcQsJN6lncVdR92eTO2nKchuOzsBa5xAPg+Ih4Y8ZFBah3AsvN8IV521vrtXMO8+S7npVbl/2C141gHtQp35Crkt6j7cMOP9txK7UDWavY/rvEmdfthevN6ErX5S6tZ67dzDfPmu5x3ONocnZ4piIhpETGB2kjlueH3M3MVsIFaoUtmHs7MQ21lL+Iaq4F1wDPN65NZTy60krV+O9cwb77LeakXOnsgUkS8Ru3odYKadvskIgYy843mI9upxwdbzV7CNXaMof4Fs9Zv5xrmzXc5L/VKJ5uCiHiJ+sf0ArCV2tnsQeDbiDhDLQy8i9ropLWs9btf37z5ruelXurc7YOImAHMpg4I+pvaVWxqZv5O7c9+mDrF7KscsbHMWLPW73598+a7npd6rYszBfuoHc2ON6/PUNt7Qp0k9ktmftmDrPW7X9+8+a7npd7K/8Fqx0sdwIQRP0+hTgycQT2683Cvstbvfn3z5ruedzh6OTq/eVFETKJOixsAPsjMreORtX7365s33/W81Lor3ZWMdVALco7SHHM8Xlnrd7++efNdzzscbY+rYabgGmqjof0R5+6F36us9btf37z5rueltnW+KZAkSe3o3COJkiSpN2wKJEkSYFMgSZIaNgWSJAno5o6GUmuiDqa5n9pe9m7gUGYuHcf6c4ChzBwcr5qSdCE2BepbEXE9sBK4JTMzIgaAteP815hDbX1rUyDpivORRPWtiLgOOAisBjZn5rHm/QHgfeAIcAMwmJkfRcQSYDmwGJgLnAa+po7AnQI8nZlnI+JR4GXgJ+AeYGlmHouItdRGNRObuluBDcAQ1RSsoU7L+1cWmEztl/8bsBeYD8xzdkFS22wK1Nci4l7qi/cJ4GfgHeBOYGZmvhoRAewGHsvMIxGxD3g8M/dExCCwODO3RcTnwApgB/Ar8FBmHoyIF6nbEyuAncCs5v1HMvO7iHgb2JeZHza1zslm5qLm56cy8/mImA78kZlD4/JLktQ3vH2gvpaZu4AFETEBeBb4FNgC3B4Rw2sLfgRuo2YOyMw9zftDwPDPJ4BJwM3UrMGC+o5nCnA2M09ExOvAxoiYSDUfo503O+LPd4+qL0mtsilQ34qIacCyzHylmfb/DFhP3eM/nZlrms/Na967GMeoWwTrm0bgJmBWRNwIHM3MJ5vZiY+B+6gv/YiIO4C/zpcdcW2n9ST1lLcP1LciYvhe/V7gT+pwmm+ATcC7wEngWqpBWBkR86k1AIuA/c3nNgNfABuBH4CFwEzqONwDwFTgPWqWYT2wnZoR2JWZmyJidnO9U8AS6tbF6OxxYB21tmBVZm7r0a9EUp+zKZAkSYCbF0mSpIZNgSRJAmwKJElSw6ZAkiQBNgWSJKlhUyBJkgCbAkmS1LApkCRJAPwDs7/BvGoW1ScAAAAASUVORK5CYII=\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Example 6b\n",
- "# This is the basic plot\n",
- "ax1 = plt.figure(frameon=True, linewidth=20).add_subplot(111)\n",
- "plt.stackplot(seasons,hpc_core_data,labels=ucores,alpha=0.75)\n",
- "ax1.legend(loc='right', shadow=True, fontsize='medium', bbox_to_anchor=(1.4,0.5), ncol=2)\n",
- "# This is basic information\n",
- "ax1.set_title('Cores per Socket evolution on HPC systems')\n",
- "ax1.set_ylabel(\"# HPC systems\") \n",
- "ax1.set_xlabel(\"Semester\")\n",
- "plt.xticks(rotation=45)\n",
- "## Annotate the plot\n",
- "#ax1.grid(True); \n",
- "#ax1.set_frame_on(False)\n",
- "#ax1.axvline(x=8 , color='b', linestyle='--')\n",
- "#ax1.axvline(x=4 , color='b', linestyle='--') \n",
- "#ax1.axvline(x=1 , linewidth=2, color='k', linestyle='-') \n",
- "#ax1.axhline(y=100,linewidth=2, color='k', linestyle='-')\n",
- "### Text in de the middle of the plot\n",
- "#plt.text(0.5, 0.5, 'pretty messy plot', \n",
- "# size='x-large', \n",
- "# horizontalalignment='center', \n",
- "# verticalalignment='center', \n",
- "# transform=ax1.transAxes)\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 212,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD7CAYAAAB68m/qAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3Xm81mP+x/HX1aaUrCehkuQ0YxCTws9WjbH3i2xpMllDRLYf+VkalWHsjCxJamwl0TRI6EQSkiVLkWnIcjLKr12dOufz++NT4xR1zrm3617ez8fjPDrn7r7v79tRn65zfa/r+gQzQ0REcl+t2AFERCQ1VNBFRPKECrqISJ5QQRcRyRMq6CIieUIFXUQkT9Sp6gkhhKbAIKCtmbVf+9iVQFNgPtAOuM7MZqczqIiIbFp1RugHAeOAUOmxRsClZnYz8DRwSxqyiYhIDVRZ0M1sDLB0g8eutZ92JNUClqUhm4iI1ECVUy6bEkKoB/QCLtjEc3oDvQHq16/frkWLFslcMqqKigpq1crd2w7KH08uZwflj+WbbxqwfHkd4AvMFoQqX2BmVX4AHYF3NnisHjAMaFed9zAziouLLZeVlJTEjpAU5Y8nl7ObKX8MM2aYwbqPdmbVqLEJ/ZMVQmgAPADcbmYzQggnJPI+IiLycytXwpFH1vx11VnlcihwGrBDCOEa4DbgMWAPYJcQAkBD/OaoiIgkwQzOOw++/77mr62yoJvZq8CrGzzcreaXEhGRqtxzD4wYAQMGwPXX+2MhzJhRndfm3l0CEZE8VVICl14Kxx0H115b89eroIuIZIEvvoCTToI2bWDkSEhkUY4KuohIZCtW+Ki8vByefRa22CKx90lqHbqIiCTHDM48E2bOhOefh912S/y9VNBFRCK65RYYNQpuuimxpYqVacpFRCSSCRPgqqvglFPgf/4n+fdTQRcRiWDOHDj1VNhrLxg2DELVG/urpIIuIpJhS5f6TdDatf0maMOGqXlfzaGLiGRQRQX88Y/w6acwcSK0bJm691ZBFxHJoIEDfVR+553QuXNq31tTLiIiGTJunG/p79ULLroo9e+vgi4ikgGffAI9e0L79nD//am5CbohFXQRkTRbtMhvgjZsCGPHQv366bmO5tBFRNKovBx69PCzWkpKoFmz9F1LBV1EJI2uuQZeeAEeeAAOPDC919KUi4hImowe7Vv6zz0XevdO//VU0EVE0uCDD+CMM3xUfvfdmbmmCrqISIotWOA3QbfeGsaMgXr1MnNdzaGLiKTQmjV+2FZpKUyZAk2bZu7aKugiIil0xRUwaZL3BW3fPrPX1pSLiEiKjBzpW/r79fPzWjJNBV1EJAWmT/eVLJ07e9OKGFTQRUSSNH8+HH887LCDdx+qE2kyW3PoIiJJKCuDE0+EH36AadNgu+3iZVFBFxFJwkUXwdSp8OST0LZt3CyachERSdADD/jHur6gsamgi4gkYOpU6NsXjjoKBg2KncapoIuI1NDXX8MJJ3j7uMcf996g2UBz6CIiNbByJXTrBsuX+wairbaKnegnKugiItVkBued52vOn30Wdt89dqL1acpFRKSa7rnHt/QPGABdu8ZO83Mq6CIi1TBpElx6qZ+ieO21sdP8sioLegihaQjhoRDC9EqP1Q8h/DWE0D+E8HAIoTi9MUVE4vniCzj5ZGjTxs9rqZWlQ+HqxDoIGAdU7lHdD5hnZn8G7gCGpSGbiEh0y5f7qLy8HMaNgy22iJ1o46os6GY2Bli6wcPHANPW/v6HQNsQQuPUxxMRiccMzjoLPvwQnngCWreOnWjTEl3l0oT1i/yStY8t2fCJIYTeQG+AoqIiJk+enOAl41u2bJnyR5TL+XM5OxRu/ieeaM6oUbvSu/c/qV//K7L+W2BmVX4AHYF3Kn09BTi40tdLgMZVvU9xcbHlspKSktgRkqL88eRydrPCzP/CC2YhmHXvblZRkfpMNVG5/m7qI9Gp/eeAAwBCCHsCH5jZz0bnIiK5aM4c6N7dD9saNgxCqPo12aA6q1wOBU4DdgghXBNCaADcBewcQrgGuAw4K70xRUQyY+lSX2Nety488wxsvnnsRNVX5Ry6mb0KvPoLv3VB6uOIiMRTUQGnnQaffQYvveRnteQSbf0XEVlr4EBfmnjXXdCpU+w0NZely+NFRDJr3Djf0t+rlx+Lm4tU0EWk4H3yCfTsCe3bw/33585N0A2poItIQVu0yG+CNmwIY8dC/fqxEyVOc+giUrDKy+HUU+HLL6GkBJo1i50oOSroIlKwrrkGJkzwvqAHHhg7TfI05SIiBWnUKLjpJm9Y0bt37DSpoYIuIgXngw/gjDPgoIN8iWK+UEEXkYKyYIHfBN1mGxgzBurVi50odTSHLiIFY80ab1Qxfz68/jpsv33sRKmlgi4iBePyy301y4gRsO++sdOknqZcRKQgjBjh8+X9+sEf/xg7TXpohC4iea20FM45px3z5kHnznDLLbETpY9G6CKS1/r3h88/b0S9er5UsU4eD2NV0EUkb02fDiNHAgRWr/abovlMBV1E8tLrr8Mhh3ijZ/BfBw6MmyndVNBFJO8MG+bnma9a9dNjZWUwfLgvWcxXKugikjfWrIFLL4Wzz4amTb2NXGXl5fk9SldBF5G8sGgRHHss3HGHL03cdlsflVdWVgZvvBEnXybk8f1eESkUc+ZAly4wdy4MHeoj9MomT55Mx44do2TLJBV0EclpL73k2/nr1IGXX/YboYVKUy4ikpPM4K9/haOOgubNfYliIRdzUEEXkRxUVubnmPftC8ccA1OnQsuWsVPFp4IuIjllwQI4/HB48EHfBfrMM7DFFrFTZQfNoYtIzvjoI/jv/4Zvv4XHHoMePWInyi4aoYtIThg/Hg44AFauhNdeUzH/JSroIpLVzODmm73L0K9+5Tc/O3SInSo7acpFRLLWypVwzjnw6KPQvTs8/DA0aBA7VfbSCF1EslJpKXTs6MV80CB4/HEV86pohC4iWWfGDJ9iWbQIxo6F44+PnSg3aIQuIlll9Gg4+GCoXdvXl6uYV19SI/QQwhVAS2ABsBtwlpn9mIJcIlJgKipgwAA/DfGgg+Dpp6FJk9ipckvCBT2E0BToD2xnZhUhhHFAN+CxVIUTkcKwfLk3bh47Fs44A+67DzbbLHaq3JPMlMsKoAxovPbrRsDHSScSkYIyb56PyJ99Fm6/3ZtTqJgnJti6/kyJvDiE04CeQCkQgAvMbNkGz+kN9AYoKipqN3r06MTTRrZs2TIaNWoUO0bClD+eXM4O6cv/0UeNue66PSgrq8V1131Chw4/pPwakPvf/06dOs0ws32rfKKZJfQB7A3MBOqs/fo24C+bek1xcbHlspKSktgRkqL88eRydrP05B8+3KxePbPWrc1mzUr5268n17//wDtWjbqczJTLTsAPZrauj3YpUD+J9xORAlBeDpdf7nPlBx8Mb73lO0AlecmscpkAHB1CuA1YBOwB9EtJKhHJS4sX+xkszz8PF17oc+Yb9v2UxCVc0M2sHLgghVlEJI99/rmflDhnDtx/P5x7buxE+Uc7RUUk7SZNghNPhBC8ZVwBtPeMQjtFRSSthgzxhhQ77ugnJaqYp48KuoikxerV0KcPXHCB9/184w1o1Sp2qvymgi4iKbdwIRxxhO/4vPJK3zTUuHHVr5PkaA5dRFLqk0+gSxf4+msYORJOOy12osKhgi4iKfPcc3DqqbD55vDqq7D//rETFRZNuYhI0szg1lt9ZN66td/8VDHPPBV0EUnKypVw+ulwxRW+NHHKFGjePHaqwqSCLiIJmz8fOnXyufI//QlGjYKGDWOnKlyaQxeRhLz3nu/8XLgQnnrKR+cSl0boIlJjY8b4GeYheJs4FfPsoIIuItVWUeFTKyedBG3bwttvwz77xE4l66igi8gmlZbCxRfvzdy5cMop3vezVy8oKYGmTWOnk8o0hy4imzRwIHz44ZZ06AA//AC33AKXXebTLZJdVNBFZKNKS73Hp1lg4UL429+gZ8/YqWRjNOUiIhvVsyeUlfnndevCtGlx88imqaCLyM+Ul/spiZMm/fTY6tUwfLivPZfspIIuIutZsgS6dvVzzGttUCHKy31OXbKTCrqI/MfcuXDAATBhAjRr5ssUKysr83PNJTupoIsIAJMnQ/v2fiN04kT46is/dMsMSkom/+fz996LnVQ2RgVdRHjgAfj976FJE98s1Llz7ESSCBV0kQK2ejVceCGcd54X9Dff9ONvJTepoIsUqB9+8F6f994Ll18O48fDllvGTiXJ0MYikQI0a5aflDhvni9FPP302IkkFVTQRQrMCy9A9+5Qv76fx/Jf/xU7kaSKplxECoQZ3H47HHss7LKLt4lTMc8vKugiBWDVKjjrLD9U67jj/AzzFi1ip5JUU0EXyXP//jf87nc+V37ddd5dSG3i8pPm0EXy2Acf+M3P77/3fp8nnxw7kaSTRugieeqZZ3yOvLwcpkxRMS8EKugiecYMBg2Cbt1gjz385me7drFTSSZoykUkj6xY4Tc/n3zSzzIfOtSXJ0phSGqEHkJoE0IYEEK4MoTwfAihQ6qCiVS2rq+lzuLeuG++gUMO8bnym26CkSNVzAtNwiP0EEJt4Hagi5lVhBBGAmtSlkykknV9LQcO9K3qsr633/bliEuXwrhx0KVL7EQSQzIj9PZAAPqGEPoDXYAFKUklUsn06X4aoFng4YfVMWdDjz/uI/PNNvMWcSrmhSuYWWIvDOEU4H6gpZktDiE8CrxsZo9s8LzeQG+AoqKidqNHj04ucUTLli2jUaNGsWMkLBfzr1xZi1NO2Z8lS+ri4wejWbMVXHXVp+y++5Kc6Tyfju99RQUMG7YLjz++M23bLuJPf/qYLbdcndJrrJOLf3Yqy/X8nTp1mmFm+1b5RDNL6AM4CphW6evzgEc29Zri4mLLZSUlJbEjJCXX8ldUmB1//Lq2Cj//2HtvswcfNFu2LHbSqqX6e79kiVnXrv59OOccs1WrUvr2P5Nrf3Y2lOv5gXesGnU5mSmXt4Bt186lA+wMfJbE+4ms57bbfC117drrP16vHhx6qI9Qe/eGHXeEiy7yEwQLwb/+5evL//EPuPtun46qVy92KskGCRd0M/sBuBK4M4RwHVAE3JGqYFLYJk6EK6/087nLy9f/vbIyWLwY3n8fXn/dD5t64AHYfXfvtDNmjDduyEevvQYdOsDXX/upiX37kjPTTpJ+SS1bNLNnzKyvmd1gZmeb2Y+pCiaF65//9ONdf/MbL1wb62sZAhx4IDz2mPe//POfvcnxSSfBzjvDgAG+lC9fPPQQHHYYbLstvPWWdxgSqUw7RSWrLFsGXbt6sX72WajufawmTeCqq/wfg/HjYe+94YYbvLCfcAK88or/Q5CL1qyBfv3gnHP8J5A334Ti4tipJBupoEvWqKiAXr18LnzUKGjVqubvUbu2T8E8/zx8/rkfF/vqqz6y/fWv4a67YNGi1GdPl//7Pzj6aM/dr5/Pm2+1VexUkq1U0CVr3HgjjB0Lt9ziBThZrVrBzTf7tM3IkbD11l4Ud9wRzj4b3n03+Wuk02efwf77w+TJMGwY3HEH1NFhHbIJKuiSFcaPh2uv9fNHLrkkte9dvz6cdppvunn3Xb/GE0/4gVX77+/FfuXK1F4zWRMnwn77eSPnSZPgzDNjJ5JcoIIu0c2eDX/4A/z2t/Dgg+ldtbHPPn6Nb775afqlVy/YaSe44gqfg4/JzJciHnUUNG/uu2QPOihuJskdKugS1eLFfhO0fn1fc96gQWauu9VWP61df+UVv9l4xx3QurUX0/Hjf75cMt3KyuDcc+Hii337/htvQMuWmc0guU0FXaIpL/eR+dy5vnY8Ro/LELyYP/UUfPmlL3WcOdO7/LRq5fP6332X/hzff+/LEIcOhf/9X7+XkMM71SUSFXSJ5vrr4bnnfOrjkENip/Fpl+uvhy++8H9gWrf24tq8OfTo4ZuY0rH08cMPfbPQ22/7mvpBg6CW/mZKAvTHRqIYMwYGD/bVJuefHzvN+urW/Wnt+qxZ0KePL4M8+GBo2xbuv9+PqU2Fv//dt/GvWuW7QHv0SM37SmFSQZeMmznTb0QecAD89a/ZvXX9V7+CO+/0m6hDh/qywfPP99H8BRfARx8l9r5mvrP1uOP8GtOnQ/v2qc0uhUcFXTJq4UIvYltuCU8/7Wd454KGDf2niRkzfKfm8cf72vA99/SDwkaN8pua1fHjj7508uqr4ZRTfGS+007pzS+FQQVdMmbNGj+j5ZtvfEXLDjvETlRzIfj68BEjfMPSX/7i58h07+43da+5BubN2/jrS0uhY0dvSjF4sP+aqZU9kv9U0CVjrrwSXn7Z56D32y92muRtt52vXf/8cz/5sEMHXxWzyy7+U8jEiX6cwbp+qBMm+LTKxx/7P2hXX53d002Se7SRWDLi0Ufh9tvhwgvhjDNip0mtWrXgyCP944svfOPSQw95b8/WraGoCGbO3JJjj4VmzXx9+V57xU4t+UgjdEm7GTP8pMBDD/Wins9atvRR+ldf+RLEbbbxIwcgYOaHa6mYS7qooEtaffedTz80aeKbd+rWjZ0oMzbbzJcgtmv3039znTpw331xc0l+U0GXtCkr82YTCxf62eZFRbETZVZpKQwf/lP3pLIy/3r+/Li5JH+poEvaXHIJTJniy/v22Sd2mswbONBvilZWXu6Pi6SDCrqkxUMPwZAhvgrk1FNjp4lj2rSfr00vK/OboiLpoIIuKffGG75d/vDDfTdkoXrvvY33QxVJBxV0Salvv/VzUFq08CYStWvHTiRSOLQOXVJm5Uro1s0PrnrpJV+yJyKZo4IuKWHmh1W99Zaf0bLHHrETiRQeTblIStx7Lzz8sPcF7dYtdhqRwqSCLkmbPBn69fO2aQMGxE4jUrhU0CUpX37pm4d2283Pa1GnHZF49NdPErZihZ8LXlbmO0EbN46dSKSw6aaoJMTMGz68/z6MHw9t2sROJCIq6JKQ227zdeaDB8Mxx8ROIyKgKRdJwIsverOKE0+E/v1jpxGRdVTQpUY+/9zbrf3mN35yoDruiGSPpAt6CKFBCGFmCOHWVASS7LV0qZ9tXquW3wRt1Ch2IhGpLBVz6IMAHTeU5yoqoFcvmDXLp1xatYqdSEQ2lNQIPYRwGjAV+Fdq4ki2GjzYGxvfeiscdljsNCLyS4KZJfbCEHYHeprZ1SGEAUAjM7v8F57XG+gNUFRU1G706NFJxI1r2bJlNMrheYZE80+dui3XXLMnv//9fPr3nx1t3jyXv/+5nB2UP7ZOnTrNMLN9q3peMgX9f4HaQBlwGFAPGGtmd27sNW3atLFPP/00oetlg8mTJ9OxY8fYMRKWSP7Zs6FDBygu9u5DDRqkJ1t15PL3P5ezg/LHFkKoVkFPeA7dzAZXulh9fIS+0WIuuWfRIuja1Yv4M8/ELeYiUrVUrHI5ATgE2D+EUKDNxvJPeTn84Q8wdy6MGQPNm8dOJCJVSXqVi5k9DTydgiySRa67Dp5/3vuCHnxw7DQiUh3aWCQ/89RTcOONcM45cN55sdOISHWpoMt6Zs6E00+HAw6Ae+7RTlCRXKKCLv+xcKHvBN1qK28jt9lmsROJSE3otEUBYM0aOOUU+OYbeO012GGH2IlEpKZU0AXw0xNfecX7gu63X+w0IpIITbkIf/sb3H479O0LZ5wRO42IJEoFvcC9846vZunY0ZtWiEjuUkEvYN995z1BmzaF0aOhbt3YiUQkGZpDL1BlZd5xaOFCmDoViopiJxKRZKmgF6h+/eD11+Hxx2GffWKnEZFU0JRLARo6FO67D664Ak7V6TsieUMFvcC88QZccAEcfjj8+c+x04hIKmnKpUCUlkKfPvuwYAG0aAFPPgm1a8dOJSKppIJeIK6/HmbNakydOlBSAltvHTuRiKSaplwKwMcf+w5QCNSqBdtuGzuRiKSDCnqeMoO33oJevWCvvbxhxToDB8bLJSLpo4KeZ1asgGHDYN99Yf/9vdtQ5SNwy8pg+HCYPz9eRhFJDxX0PPHpp762fKed4OyzvXAPGeLLEje8+VlerlG6SD7STdEctmYN/P3vXrhfecW37p94IvTpAwce6CPzffbx4l5ZWZkvXxSR/KKCnoO+/dY3Bw0d6ueXN28OgwfDWWfB9tuv/9z33vvp88mTJ9OxY8eMZhWRzFFBzxFmMHmyj8afecanTY480r8+5hitKRcRFfSst3gxjBzphXv2bNhmG7jkEjj3XGjdOnY6EckmKuhZ6v33vYg/9pivXOnQAR55BE4+GRo0iJ1ORLKRCnoWWbnSlxkOGQLTpnnh7tEDzj8f2rWLnU5Esp0KehaYOxceeMDXjy9cCMXFcMcdvilIW/RFpLpU0CMpL4cJE3w0/sILUKsWdO3qSw47d15/M5CISHWooGfY99/7SPz+++HLL73927XXel/PZs1ipxORXKaCngFmPic+ZAg89ZRv7OnUCW691Ufl6uUpIqmggp5Gy5b5KpUhQ2DmTGjc2Jcbnnce7L577HQikm9U0NPgk0+8xduIEbB0KbRt6zc9e/SARo1ipxORfKWCniJlZfDss17IJ0+GevV8zXifPn7qoW5yiki6qaAn6euv4cEH/VyV+fOhZUu46SY480woKoqdTkQKScIFPYSwKzAIeBdoBiw0sxtSFSzblJbCxRfvzYsvQpMmfrrhfff5aYcVFXD00T4aP+IInasiInEkM0LfBnjSzMYBhBA+CSE8Z2YzUhMtuwwcCB9+uCUnngj//jfMmQPbbQeXX+43OnfZJXZCESl0CRd0M5u+wUO1gOXJxclOL77o0ypmgalTvRvQo4/62eObbRY7nYiIC2aW/JuEcDzQ0cwu/oXf6w30BigqKmo3evTopK+XCatW1aKkpAnjxu3I7NmNAQMCtWtXcOyxpfTrNyd2xBpbtmwZjXJ4mU0u58/l7KD8sXXq1GmGme1b5RPNLKkPoBNwN1CrqucWFxdbtpszx+yyy8y23toMzFq3Nqtb1z9f99GggVlpaeykNVdSUhI7QlJyOX8uZzdT/tiAd6wa9TipnqIhhGOAI4CLgaYhhAOSeb9Y1qyBceP8huZuu8Fdd8Fhh0FJif+64ZJD9eQUkWyUcEEPIbQDRgH7AyXAOKBNinJlxPz53rqtVSs47jj4+GO44QaYNw9Gj4aOHeHNN9WTU0RyQzI3RWcAOTcpZQZTpvh2/Kef9tH5YYf5qLxLF6izwXdEPTlFJFcUzMaiJUt8ZcqQIT4S32or6NvXz1UpLo6dTkQkeXlf0D/80Iv4o4/6YVnt2vnxtd27w+abx04nIpI6eVnQV62CsWO9kL/+OtSv7wW8Tx9o3z52OhGR9Mirgv7ll36q4UMPeSOJXXf1M8dPPx223TZ2OhGR9Mr5gl5RARMn+mj8uef8sS5dfDR+2GHe2k1EpBDkbEFfsACGD/dWbnPn+oFZ/ftD797QokXsdCIimZdTBd0M3n7bR+OjRvlc+SGH+Frybt38DHIRkUKVEwV9+XJ44gk/rvbdd73rz1lnwfnnwx57xE4nIpIdsrqgf/qpF/FHHoHFi2HPPX103rMnbLFF7HQiItkl6wr66tXeNGLIEJg0CerW9WNq+/SBAw9UKzcRkY3JmoL+7bfexu3BB/3zFi3gxhu9ldv228dOJyKS/aIWdDM/0XDIEG+wXF4ORx7pK1eOPlqt3EREaiKjBf2rrzZn/nzfuTlypM+Pz54N22wDl17qrdx23TWTiURE8kdGC/qPP9amc2ff0bliBey3H4wYASedBA0aZDKJiEj+yfiUy6xZ0KMHXHYZ/Pa3mb66iEj+SklP0WpfLGxnsLPBDwvgi3kZu3DqbAcsiB0iCcofTy5nB+WPrY2ZVblYO8Mj9IUzzBZU3eg0S4UQ3rHqNGrNUsofTy5nB+WPLYTwTnWep6OrRETyhAq6iEieyHRBfzDD10s15Y8rl/PncnZQ/tiqlT+jN0VFRCR9NOUiIpInMrLKJYTQFBgEtDWznOrqGULYFc/+LtAMWGhmN8RNVX0hhFrAeOAtoB6wK3Cmmf0YNVgNhRAa4P8NE83s8th5aiKE8Cawcu2X5Wb2u5h5aiqE0AY4FfgROBQYYGZvx01VPSGElsArwFdrH2oMzDSz0yNFqpEQwhVAS3zJ5W7AWZv6u5upZYsHAeOAvTN0vVTaBnjSzMYBhBA+CSE8Z2YzIueqiWlmNggghDAO6AY8FjdSjQ0C3osdIkETzGxA7BCJCCHUBm4HuphZRQhhJLAmcqyaWAqca2YvA4QQ/gS8FDdS9awdCPcHtlv7va/y725GCrqZjQkhdMzEtVLNzKZv8FAtYHmMLIkwswq8GBJCqIP/lPFp1FA1FEI4DZgK7AU0ihwnEXuGEK4EGgDTzey52IFqoD0QgL4hhM2BhcDQuJGqz8wWAuuK+WbAvmZ2fdxU1bYCKMN/qliE/9n/eFMvyJrjc3NBCOF44EUzmx07S02FEI4ALgH+YWbV2qSQDUIIuwO/NrOrQwh7xc6ToJvN7O21o93XQghLzey12KGqaWfgAOBUM1scQngULzKPRE2VmB7AE7FDVJeZLVk75TIqhFAKfA18vqnX6KZoNYUQOgGd8KKYc8zsRTM7EtglhNAndp4aOB5YGUK4Cp+66xBC6Bc5U42sm282s3JgCv7nKFcsAWab2eK1X78OdIwXJyknAaNih6iuEMLewBXAMWvn/BcA123qNRqhV0MI4RjgYOBiYIcQws5mNi1yrGpZO8LdpdKP+f8CWkWMVCNmNnjd5yGE+kAjM7szYqQaCSH8CjjQzIatfWg3YGzESDX1FrBtCKH22n+QdgY+i5ypxtYOyN4ws9Wxs9TATsAPZrbunkUp0GJTL8jIOvQQwqHAH4EjgfuA23JllUUIoR3wKrBumqIhcK+ZPRItVA2sXaVzC75Kpy7wa+AiM5sfNVgNhRBOAC7AV+rca2Y58aNzCGFH4F78+98Y/39w6dp7Gzlh7VRjZ+B7vKD0zZW/v+uEEJ7Ac+fMAV1rp+juxldILQL2APqZWelGX6ONRSIi+UFz6CIieUIFXUQkT6igi4jkCRXULxWQAAAAIUlEQVR0EZE8oYIuIpInVNBFRPKECrqISJ5QQRcRyRP/D837+eCfF0QFAAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Example 7\n",
- "## More decorations\n",
- "\n",
- "import matplotlib.pyplot as plt\n",
- "\n",
- "x = [1,2,3,4,5,6,7,8] #fake data\n",
- "y = [1,2,3,6,5,7,9,12]\n",
- "\n",
- "fig = plt.figure()\n",
- "ax = plt.subplot()\n",
- "\n",
- "ax.plot(x, y, 'b', marker='^')\n",
- "ax.grid()\n",
- "ax.margins(0) # remove default margins (matplotlib verision 2+)\n",
- "\n",
- "#ax.axvspan(0, 4, facecolor='green', alpha=0.6)\n",
- "#ax.axhspan(4, 9, facecolor='yellow', alpha=0.4)\n",
- "#ax.axvspan(9, 12, facecolor='red', alpha=0.3)\n",
- "\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 81,
- "metadata": {
- "scrolled": true,
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD7CAYAAACRxdTpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAHnRJREFUeJzt3Xl4VeW59/Hvk4kQMmBIQggEwjwT1FhBRbBYJ+DUqVq1Pe057Wvr6aDt21q1nlZbW4fayZ7W1tq3todqrdUOihNFCaKABJmRhDEQpmyGDBAy7vv9I1ubRiA7Idkre+3f57pyXVkra+/7TrLzy9rPetZazswQERF/ifO6ARER6X4KdxERH1K4i4j4kMJdRMSHFO4iIj6kcBcR8SGFu4iIDyncRUR8SOEuIuJDCV4VzsrKsoKCAq/Ki4hEpVWrVh00s+yOtvMs3AsKCigpKfGqvIhIVHLOlYeznYZlRER8SOEuIuJDCncRER9SuIuI+JDCXUTEhxTuIiI+pHAXEfEhhbuIRD3dLvSDFO4iErVq65v46tNrmHb/IvZVH/e6nV7FszNURUROpuCOBZ1+zPT7X+vU9jsfmNPpGtFEe+4iIj6kcBcR8SGFu4iIDyncRUR8SOEuIuJDCncRER9SuItIr1JT3+R1C76gcBeRXmNV+RGu+OkbXrfhCwp3EfFcS9D4n9e2cN2vlnndim8o3EXEU/ur67np8eU8/GoZl0/K5cVbZ3jdki/o8gMi4pmFmw7w9T+vpaEpyEPXTuFjZw/BOed1W76gcBeRiKtvauH+F9/ld8vKmZiXziM3nMnI7FSv2/IVhbuIRNSWA7V86anVbN5fy2cuGM7tl42lT0K81235jsJdRCLCzHjq7d1854WN9EtK4Lf/cQ4Xjc3xui3fUriLSI+rrmvijufW8dKG/cwYncUPryskJy3Z67Z8TeEuIj1q5c7D3PrUaiprG7jz8nH8nxkjiIvTQdOepnAXkR7R3BLkf17fyiOLtpCfmcKzt5xHYX5/r9uKGQr3Hna0oZmEOEdyog4YSezYU3Wcr/xxDW/vPMzVZw7mO1dOIrVP74qbqrpG+qcked1Gj+ldP22faQka//azpRw82sD15+Tz79MLyM9M8bot6UEb9lTz1raDnDcyiwmD0mNy+OHlDfv4xrPraW4J8uPrC7nqzCFet3RC33/xXR66ttDrNnqMwr2TunJvR4Bfv7GDX7+xI6xt/X5vx2jT1d95Z/jhd368sYXvLtjEkyt2UTgkg59+/EwKsvp53dZJ/amkgqvPGsK0EQO8bqVHKNxFpMvMjJ2H6liz+wi/eH0bWyqP8rmZI/i/HxlLUkLvvrpJfmZf7vrLel66dYYv59kr3EXkhLr6juVXxdv5VfH2sLb18h3Ldz86iU//diWPLt7GbReP8ayPntK7/7XGKDPzugWJsCt++gYPvryZ5dsP0dQS9LqdmDBrbA7zCvP4xevb2Fp51Ot2up323HuhS3+yhE+dV8BVZw4mJUm/oliQlpzAr5ds59HF20jtk8D5owYwc0wOM8dmM7h/3x6vb2bsqTrOmt1VrNlVxerdVT1eszf41twJFJdW8s2/rOePN0/z1UXLlBy9UGJ8HN/8ywYefGmzZtnEiKc/N53a+ibe3HqI4rIAS8oCvLLxAACjclKZNSabmWOzOacgs1um1R5taGZdRRWrd1W1BvruKgK1DQD0SYhj0uCM064RDbLT+nDnFeO587n1PLOqguuK8r1uqdso3HuhF750AavKj/Dbt3by/97cyeNLd3Dx+IH8x3kFTB85wFd7F/JPacmJXDYpl8sm5WJmbAscZXFpgOKyAL9fVs7jS3eQnBjH9BEDmDkmm1ljc8KajdISNLZU1rImFOSrd1WxpbKWYGj0b3hWP2aMymLq0P5Mze/PuNx0khLiIjJLqDe4viif596p4PsvvsvscTkMSO3jdUvdIqxwd85dDFwNVAJmZve2+/pw4GFgJTAVeNLM/t7NvcYM5xxFBZkUFWSyr/o4f1i+iyff3sXCTQcYMzBVQzYxwDnHqJw0RuWk8dkZI6hrbGbF9sMUl7WG/evPb4LnNzFsQAozx2Qzc0w200cOICUpgcra+veHVtbsqmJdRRXHGlsAyOibyNT8/lw2KZczQ2Hu5xN5whEX5/j+VZO54pE3uG/Bu/z4+qlet9QtOkwH51wK8Etgopk1OOeedc7NNrNFbTa7HVhqZj92zp0J/AlQuHeDQRl9+dqlY/nih0fx/Nq9PPHWzveHbD7+oaF8ctowDdnEgJSkBC4al8NF41qvolh+6Fhr0JcGeKakgt8vKycpPo7Mfknsr6kHICHOMX5QOtecPYSp+a1BPjyrn975ncDogWl8fuZIfvbaVq4+azAzRmd73dJpC2fXbzpQbmYNoeU3gTlA23A/ALz308gGVnVbhwJAcmI8HyvK59qzh1BSfoQn3trJb5bu4PE3tjNbQza+1ZmhkcaW4PvBDtAcNNbvqWb9nmp+v6z8pI/zwwlU3eELF43ihXX7uPuvG3jltguj/pIh4UyFzAFq2yzXhNa19SPgXOfcj4BvAb890RM55252zpU450oCgUBX+o15zjnOKcjk5zeexdJvXMQts0ZSsvMwNz6+gkt/soQnV+yirrHZ6zZFok5yYjzfu3IS5Yfq+NlrW7xu57SFE+6VQFqb5fTQuraeAB43s68CVwFPO+cy2z+RmT1mZkVmVpSdHf1ve7w2KKMvX790HMvunM1D104hIS6Ou/6ynun3v8b3X3yX3YfrvG5RJKqcNyqLq88azK+Kt1O6v7bjB/Ri4YT7MmCYc+69Q8jnAwucc5nOufTQunxgX+jzI0AwzOeWbpCcGM91Rfks+PIFPPP56VwwKovfLN3BzB+8zqOLt3ndnkhUuXvOBNKSE7jrL+sJBqP3hMIOx9zNrM45dwvwiHMuAKwzs0XOuYeAw8ADwFeA25xz5wHDgbvM7GBPNh6rOjs97cGXN/Pgy5vD3l7jrxLrMvsl8c05E/jaM2t58u1dfGLaMK9b6pKw5tKZ2UJgYbt1t7f5fCmwtHtbExHxxjVnDea5dyp48OXNXDJhIDnp0XdLQA2diIi045zjvisn0dAc5N4XNnndTpco3EVETmBEdipfvGgUC9bt4/XN7eeQ9H4KdxGRk/j8zJGMyknl7r9uiLopxgp3EZGTSEqI4/6rJ7On6jg/+Ud0zX1XuIuInMI5BZnc8KF8frN0Bxv3VnvdTtgU7iIiHbjjsvGckZLInc+tpyVK5r4r3EVEOpCRksh/z53Auopqfr9sp9fthEXhLiIShn8rzOPCMdk8/Eope6uOe91OhxTuIiJhcM7xvSsn0WLGPX/f6HU7HVK4i4iEKT8zhVtnj+HVTQd4ZeN+r9s5JYW7iEgnfHbGcMblpvHtv22ktr7J63ZOSuEuItIJifGtc98P1Nbzw1fLvG7npBTuIiKddObQM/jktGH8btlO1u6u8rqdE1K4i4h0wdcuHUt2ah/ufG49zS1Br9v5gLAu+Sut1lX0zv/QItJ9OnvPhMraBkZ986VOPSYS903QnnsnzF9+8psMi4j0Jgr3MFXXNfH3tXu9bkNEJCwK9zA9+04F9U29b1xNROREFO5hMDPmryhnan5/r1sREQmLwj0My7YdYnvgWNTeKFdEYo/CPQzzV5ST0TeRuVMGed2KiEhYFO4dqKyp59WNB7iuaAjJifFetyMiEhaFewf+uHI3zUHjxnM1JCMi0UPhfgrNLUGeensXM0ZnMTyrn9ftiIiETeF+Cq9trmRfdT03aa9dRKKMwv0U5q/YRW56MhePz/G6FfHIoaMNXrcg0iUK95MoP3SMJWUBPv6hfBLi9WOKVW9sOeh1CyJdotQ6iT+s2EV8nOPj5wz1uhXxUHFZwOsWRLpE4X4C9U0tPFOym4+MH0huRrLX7YhHgkFjicJdopTC/QReXL+PI3VNfHK6DqTGsg17qzl0rNHrNkS6ROF+AvOXlzMiqx/njRzgdSsRFwya1y30GotLAzjndRciXaNwb2fT3hre2VXFjecOxcXgX/bKnYe9bqHXKC4LMGVwhtdtiHSJwr2d+SvK6ZMQx7VnD/G6FU+8sG6f1y30ClV1jazedYSZYzUNVqKTwr2N2vom/rp6D/MK8+ifkuR1O554cf2+Xnk/yEhbuvUgQYOZY7K9bkWkSxTubfx19R7qGlti+tK+h441sny7hmYWlwbI6Juoa/hL1FK4h5gZ/7u8nEmD0ykcErvjrKl9Eng+xm8nGAwaxWUBZozOIj4u9o67iD8khLORc+5i4GqgEjAzu7fd1x3wpdBiAdDfzP6zG/vscSt3HqHswFEevGZyTB5Ifc8lEwby0oZ9fPfKSSQlxOb//nf31xCobWCWxtslinUY7s65FOCXwEQza3DOPeucm21mi9ps9gmgysx+H3rMlJ5pt+fMX15OWnIC8wrzvG7FU/MK83hu9R6Wbg3w4XEDvW7HE4tLW09cunBMlsediHRdOLtm04FyM3vvCkpvAnPabXMTkOmc+7Jz7vvA0W7ssccdPNrASxv2cc1ZQ0hJCuvNjG+dPyqLjL6JPL82dmfNFJcFmJiXTk6azk6W6BVOuOcAtW2Wa0Lr2hoGpJvZI8ATwMvOuQ/ctsg5d7NzrsQ5VxII9J7Tuv9UspumFuMT03QdmaSEOC6flMvCTQeob2rxup2Iq6lvYlX5Ec2SkagXTrhXAmltltND69qqAVYAmFlZaJv89k9kZo+ZWZGZFWVn944/npag8eSKXUwbkcmonLSOHxAD5k7J42hDM4tL2/+a/e+trQdpCZrG2yXqhRPuy4Bhzrk+oeXzgQXOuUznXHpo3SJgBEBoXTywv7ub7QlLygJUHDke09Mf25s2IpOs1KSYHJpZXBogrU8CZw7VFEiJbh0OMJtZnXPuFuAR51wAWGdmi5xzDwGHgQeAB4GHnHN3ASOBT5lZfU823l3mLy8nK7UPl0zI9bqVXiMhPo7LJw3imVW7OdbQTL8+sXEcwqx1CuQFo7NI1DX8JcqF9VdrZguBhe3W3d7m82rgc93bWs/bfbiO10or+cKsUTE77e9k5hXm8b/Ly/nHuwf46NTBXrcTEWUHjrKvup5bZ/eOIUOR0xHTifbU27twwA3n6kBqe0XDziA3PTmmrjVTXNZ6jGHmWIW7RL+YDffG5iB/KtnNh8cNZHD/vl630+vExTnmTBlEcWmA6uNNXrcTEYtLA4wdmMagDL0eJPrFbLi/vHE/B482avrjKcwrzKOxJcjCTQe8bqXHHWtoZuXOw8zSXrv4RMyG+/zl5QzNTOHC0fpjPpnCIRnkZ/aNiWvNvLXtEE0tpvnt4hsxGe5lB2p5e8dhbjx3KHG6MNRJOeeYOyWPpVsPctjnt5srLqskJSmeooJMr1sR6RYxGe5/WF5OUnwcH4vRG3J0xrwpebQEjZc3RMVpC11iZiwuDXDeyCzNmhLfiLlX8rGGZp57Zw9XTM5lQGqfjh8Q48YPSmNEdj9fD81sP3iMiiPHNd4uvhJz4f63NXupbWjmk9N1Rmo4nHPMm5LH8h2HqKyJivPSOu29q0BqvF38JKbC3cyYv7yccblpnDX0DK/biRrzCgdh1noLPj8qLgswMrsf+ZkpXrci0m1iKtxX765i074aPjFtWEzfkKOzRuWkMS43jed9eELT8cYWlm8/pAuFie/EVLjPX15Ov6R4rjwzNk6n707zCvNYVX6EPVXHvW6lWy3fcYjG5qCGZMR3Yibcjxxr5IV1+7jqrMGkxsiFsLrT3CmDAFiwzl8HVotLAyQnxvGh4ZoCKf4SM+H+51UVNDYHdWnfLho2oB+FQzJ8d62ZxaWVTB8xgOTED9xbRiSqxUS4B4PGH1aUUzTsDMblpnf8ADmhuVPyWFdRzc6Dx7xupVvsPHiMnYfqNN4uvhQT4f7mtoPsPFSn6Y+nac57QzM+mTVTXKYpkOJfMRHu85eXM6BfEpdN0g05Tkde/74UDTvDNyc0FZcFKBiQQkFWP69bEel2UXlkseCOBV163Ni7Xw57250PzOlSDb+bV5jHt/++kS0Hahk9MHrvOVvf1MJb2w5yfdEHbvUr4gsxsecu3efyybnEOaJ+zvvKnYepbwpqvF18S+EunZKTlsy0EQN4Ye1ezMzrdrpscWmApIQ4po0Y4HUrIj1C4S6dNq8wj+0Hj7FpX43XrXRZcVmAc4dn0jdJUyDFnxTu0mmXTcwlIc7x/NroHJqpOFLH1sqjmiUjvqZwl047o18SF4zO4oV10Tk0894USI23i58p3KVL5k7Jo+LIcdbsrvK6lU5bXBpgcP++jMzWFEjxL4W7dMklEweSFB8XdUMzjc1B3tp6kFljs3VlUPE1hbt0SXpyIrPGZrNg/V6CwegZmikpP8yxxhaNt4vvKdyly+YW5nGgpoGVOw973UrYissCJMY7zhuV5XUrIj1K4S5ddvH4HPomxvN8FF0GuLg0QNGwTF32WXxP4S5dlpKUwIfH5/DS+v00twS9bqdD+6vr2by/VjfClpigcJfTMm9KHoeONbJs+yGvW+lQcVklADMV7hIDFO5yWmaNzSa1TwIvRMGsmeKyALnpyYyN4gueiYRL4S6nJTkxnksmDOSlDftobO69QzPNLUHe2KIpkBI7FO5y2uYV5lFT38zSrQGvWzmp1burqK1v1hRIiRkKdzlt54/KIqNvYq8+oWlxaSXxcY7zR2sKpMQGhbuctqSEOC6flMurG/dT39TidTsntLg0wNlDzyA9OdHrVkQiQuEu3WLulDyONbawuLTS61Y+oLK2no17azRLRmKKwl26xbQRmWSlJvXKoZklZQcB3QhbYktY4e6cu9g59wvn3D3OuW+fYrubnHPmnEvtvhYlGiTEx3HF5EEs2nyAYw3NXrfzL4rLAmSn9WFiXrrXrYhETIfh7pxLAX4JfMXM7gGmOOdmn2C78cCEbu9QosbcKXnUNwX5x7sHvG7lfS1B440tAS4crSmQElvC2XOfDpSbWUNo+U1gTtsNQv8Abgfu7d72JJoUDTuD3PTkXjU0s7aiiqq6Jl1yQGJOOOGeA9S2Wa4JrWvre8B3zazxVE/knLvZOVfinCsJBHrvnGjpmrg4x5wpg1hSFqD6eJPX7QCts2TiHMzQFEiJMeGEeyXQ9nzt9NA6AJxz+cAZwHXOuTtCq7/qnCtq/0Rm9piZFZlZUXa29qT8aF5hHo0tQV7duN/rVoDW8fap+f3pn5LkdSsiERVOuC8Dhjnn+oSWzwcWOOcynXPpZrbbzD5tZg+Y2QOhbX5kZiU90rH0aoVDMsjP7MsL67wfmjl0tIF1FVXMHKN7pUrs6TDczawOuAV4xDl3H7DOzBYBdwD/9d52zrls59zdocXbnXODe6Jh6d2cc8ydksfSrQc5fOyUo3Q9bunWg5ih8XaJSWHdscDMFgIL2627vd1yALgv9CExbN6UPB5dvI2XNuzjpnOHedbH4tIAmf2SmDw4w7MeRLyi29FItxs/KI2R2f249++beHrlbibmZTB5cOvHmNxU+iTE93gPwaCxpCzAhaOziIvTFEiJPQp3CVvBHQs6/Zh1FdWsq6jmqTC23fnAnI43CtOGvdUcOtaoSw5IzFK4S6/x9WfWMmlwBpMGZzBhUDp9k7q+h19cGsA5uHC0wl1ik8Jdeo3XNlfyzKoKAOIcjMpJZVJoOOe9wO8X5o2tF5cFmDw4gwGpfTreWMSHFO7Sa5TcfTH7a+pZX1HNhj3VbNhbwxtbDvLcO3sAcA5GZqcyKS/9/T38iXnppLW7jG91XROrdx3hixeN8uLbEOkVFO7SazjnGJTRl0EZfblkYu776w/U1LNhTzXr91SzYU8Ny7cf5q9r9r7/9RFZ/Zg4OIPJg1tDf9ehOoKmG2FLbFO4S683MD2ZgenJzB4/8P11gdoGNuytZkNFa+i/U36E59f+M/Az+iYyNf8ML9oV6RUU7hIVOjtTp/p4EyPvejHs7btzpo5Ib6CbdYiI+JDCXUTEhxTuIiI+pHAXEfEhhbuIiA8p3EVEfEjhLiLiQwp3EREfUriLiPiQwl1ExIcU7iIiPqRwFxHxIYW7iIgPKdxFRHxI4S4i4kMKdxERH1K4i4j4kMJdRMSHFO4iIj6kcBcR8SGFu4iIDyncRUR8SOEuIuJDCncRER9SuIuI+JDCXUTEhxTuIiI+pHAXEfGhhHA2cs5dDFwNVAJmZve2+/o3gFxgP3A28C0z29zNvYqISJg6DHfnXArwS2CimTU45551zs02s0VtNksFvmpm5py7HvgBMK9nWhYRkY6EMywzHSg3s4bQ8pvAnLYbmNl/m5m1ec6j3deiiIh0VjjDMjlAbZvlmtC6D3DOJQGfAr5w+q2JiEhXhbPnXgmktVlOD637F6FgfxT4ppltO9ETOeduds6VOOdKAoFAV/oVEZEwhBPuy4Bhzrk+oeXzgQXOuUznXDqAc64v8CvgR2a2yjl3zYmeyMweM7MiMyvKzs7ujv5FROQEOhyWMbM659wtwCPOuQCwzswWOeceAg4DDwB/ACYBw51zAP2AZ3uubREROZWwpkKa2UJgYbt1t7f5/Opu7ktERE6DTmISEfEhhbuIiA8p3EVEfEjhLiLiQwp3EREfUriLiPiQwl1ExIcU7iIiPqRwFxHxIYW7iIgPKdxFRHxI4S4i4kMKdxERH1K4i4j4kMJdRMSHFO4iIj6kcBcR8SGFu4iIDyncRUR8SOEuIuJDCncRER9SuIuI+JDCXUTEhxTuIiI+pHAXEfEhhbuIiA8p3EVEfEjhLiLiQwp3EREfUriLiPiQwl1ExIcU7iIiPqRwFxHxIYW7iIgPKdxFRHxI4S4i4kMKdxERH0oIZyPn3MXA1UAlYGZ2b7uvJwMPA3uA0cADZlbWzb2KiEiYOgx351wK8Etgopk1OOeedc7NNrNFbTa7DdhlZg855yYDvwFm9EzLIiLSkXCGZaYD5WbWEFp+E5jTbps5wDIAM1sPFDrn0rutSxER6RRnZqfewLkbgOvN7MrQ8meBWWb2iTbblIa2WRNarghts7Xdc90M3BxaHAuUdtc3EoYs4GAE66m2aqu2aveEYWaW3dFG4Yy5VwJpbZbTQ+s6uw1m9hjwWBg1u51zrsTMilRbtVVbtf1S+1TCGZZZBgxzzvUJLZ8PLHDOZbYZellA6/ANoTH3tWZW0+3diohIWDrcczezOufcLcAjzrkAsM7MFjnnHgIOAw8APwUeds7dDYwCPtOTTYuIyKmFNRXSzBYCC9utu73N58eBL3Rva93Ok+Eg1VZt1VZtL3R4QFVERKKPzlAVEfGhsIZlollHZ9f2cO1c4D6g0MzOiWDdkaG67wBDgENm9p0I1o8DngdWAEnASOA/Q8N3kajfN1T7VTP7WiRqtqm9HKgPLbaY2ewI1h4L3AAcB2YC95jZ2xGoWwAsAnaHVqXTemzu0z1dO1T/60ABrdMRRwOfieBr7SvAYOAY0Ae403rLcIiZ+fYDSAG2An1Cy88CsyNY/1pgHlAS4e/7HOCjbZY3AWdHsH4ccHeb5b8BN0Ww/g+B3wEPR/LnHqp9T6RrhurG0zprLS60PAjIjlDtAcDFbZbvBS6IUO1cWid2vPd9R+y1BkwF1rRZfha4yovf/4k+/D4sE87ZtT3GzP4M1EaqXpu6K83sb21WxdG6ZxGp+kEzuw/AOZdA67uHiJyw5pz7JK2/5x2RqHcCk51z33DO3eOci9hrjdZ/6A74knPuTlp3KiJyYo2ZHTKzfwCEpkwXmdnSSNQG6oBGWt8tAKQCGyNUezT/fLcCsB2I2Du1jvh9WCaHfw3XmtC6mOGcuwp4xcw2e1D7UuArwAtmVhKBehOA8WZ2l3NuSk/XO4kHzext51w8sMQ5V2tmSyJQdxitOzM3mFm1c24+raH3RARqt3Uj8FSkiplZTWhY5mnn3D6ggtZ365GwErg/dOHEBqCIfw17T/l9zz2sM2f9yjl3EXARrQEbcWb2ipldBgx3zv1XBEpeBdQ75+4ALgA+5Jy7LQJ132ehMW4zawHeoPXnHwk1wGYzqw4tLwVmRah2Wx8Dno5UMefcVODrwBxrHeM/CHwrErXNbCetl1P5b+BWWt8x7IpE7XD4fc/9/bNrQ0Mz5wO/8LiniAgNCcyg9UU3yDk3zMyWRaj2BGC4mS0IrdoBjOjpumb2vTY9JAOpZvaTnq7bpuY44Hwz+01o1WjguQiVXwEMcM7Fh/6xDAMietnt0M7EW2bWFMGyg4HDZtYcWt4HDI1g/cNm9k2A0Luln0ew9in5fp67c+4jtB7YDABNFtnZMjOBfwcuAx4FfmgROIrvnDsbKAbeGwrpB/zczJ7o6dqh+iOBH9A6WycRGA982cz2R6j+NbSeVJdE6/cdkWEC51werX/c79D6LjER+KqZBSNU/yrgw7S+1ocCX4rE661N/adCNSN2Ea3Q8NcjtM5QqgImAbeZ2b4I1V9C6zu0BmBT6Dhbr+D7cBcRiUV+H3MXEYlJCncRER9SuIuI+JDCXUTEhxTuIiI+pHAXEfEhhbuIiA8p3EVEfOj/A0BCcLBiLJZxAAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "## Example 8\n",
- "## Combined plot\n",
- "import numpy as np\n",
- "import matplotlib.pyplot as plt\n",
- "\n",
- "fig = plt.figure()\n",
- "ax = fig.gca()\n",
- "xs = np.arange(10)\n",
- "ys = np.random.rand(10)\n",
- "ax.set_xticks(np.arange(10))\n",
- "\n",
- "mybar = ax.bar(xs, ys)\n",
- "mylines, = ax.plot(xs, ys)\n",
- "\n",
- "#mylines.set_color('yellow')\n",
- "#mylines.set_marker('^')\n",
- "#mylines.set_markersize(16)\n",
- "#mylines.set_linewidth(4)\n",
- "#\n",
- "#print(len(mybar.get_children()))\n",
- "#\n",
- "#mybar.get_children()[3].set_color('purple')\n",
- "#\n",
- "#ax.set_facecolor('orange')\n",
- "#ax.set_alpha(0.5)\n",
- "\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "skip"
- }
- },
- "source": [
- "#### HELP with colors? \n",
- "\n",
- "[Color ][1]\n",
- "\n",
- "<!-- \n",
- "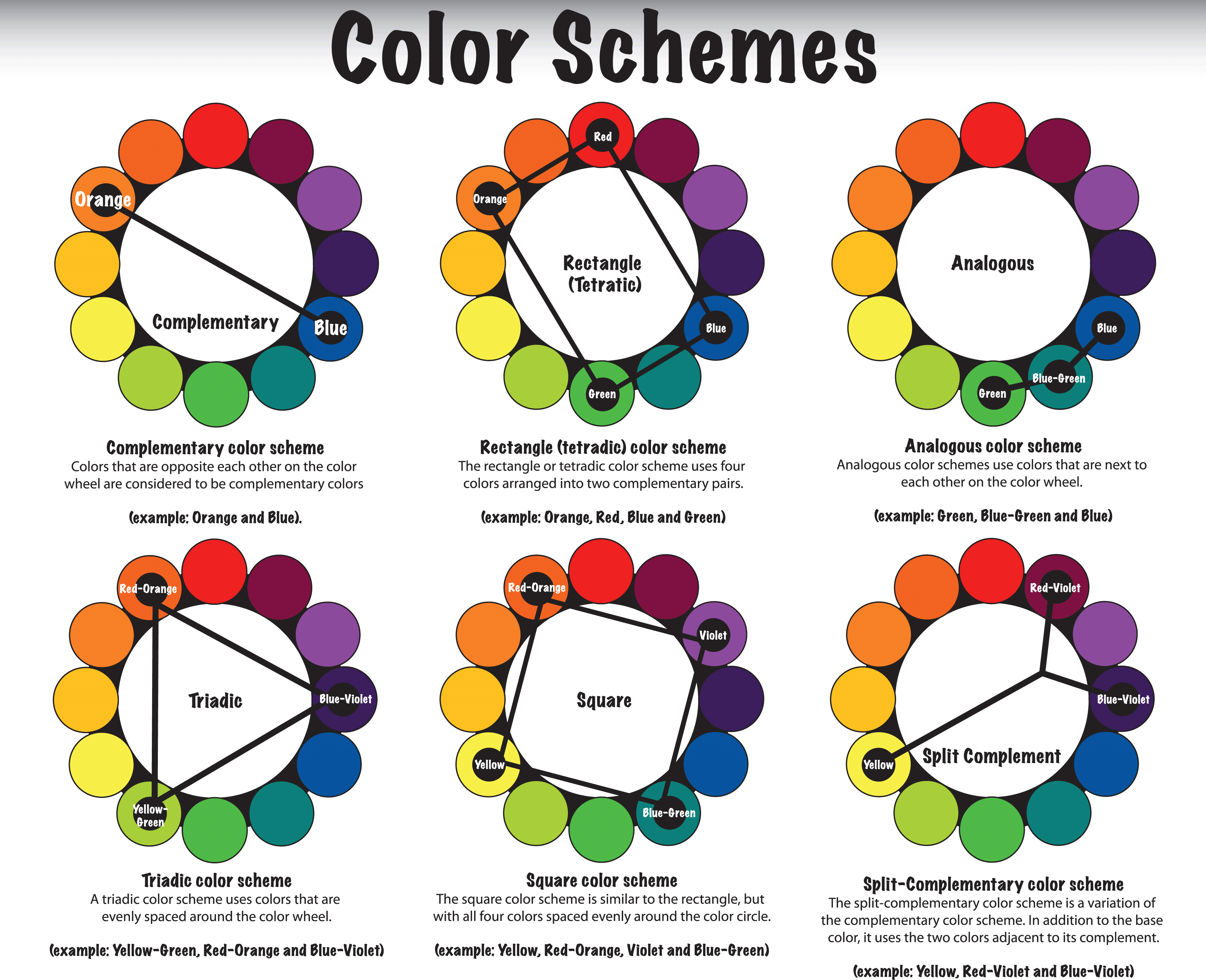\n",
- "-->\n",
- "\n",
- "[Video: Understanding color (harmonies)][2]\n",
- "\n",
- "[1]: https://oss.adm.ntu.edu.sg/limh0131/wp-content/uploads/sites/413/2015/10/059c1fb7c18c3b2314ca5a0b3e56780d.gif\n",
- "[2]: https://www.youtube.com/watch?v=Qj1FK8n7WgY&t=1s\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 98,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAArMAAAHICAYAAABd6mKEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsvWmMI+l55/kP3leelZXZdVcedVd3VXWdKcsaz3gga9Q+BpKMgez5YEPQGoZhQJ/WgN1rew1YtgwLPhbQF8GCAdmwDdjSLixgbUCyZ62j1VK3+nJ3tVzFI++LmckreATJiP1AvVFBMkhGBCMYB58fUOhqFpMRTJIRPz7xvM+fkyQJBEEQBEEQBOFGfHbvAEEQBEEQBEEYhWSWIAiCIAiCcC0kswRBEARBEIRrIZklCIIgCIIgXAvJLEEQBEEQBOFaSGYJgiAIgiAI10IySxAEQRAEQbgWklmCIAiCIAjCtZDMEgRBEARBEK4loPP+FBdGEARBEARBWA2n9Y5UmSUIgiAIgiBcC8ksQRAEQRAE4VpIZgmCIAiCIAjXQjJLEARBEARBuBaSWYIgCIIgCMK1kMwSBEEQBEEQroVkliAIgiAIgnAtJLMEQRAEQRCEayGZJQiCIAiCIFwLySxBEARBEAThWkhmCYIgCIIgCNdCMksQBEEQBEG4FpJZgiAIgiAIwrWQzBIEQRAEQRCuhWSWIAiCIAiCcC0kswRBEARBEIRrIZklCIIgCIIgXAvJLEEQBEEQBOFaSGYJgiAIgiAI10IySxAEQRAEQbgWklmCIAiCIAjCtZDMEgRBEARBEK6FZJYgCIIgCIJwLSSzBEEQBEEQhGshmSUIgiAIgiBcC8ksQRAEQRAE4VpIZgmCIAiCIAjXErB7BwiCGD8kSUK9Xkez2YTf74fP54Pf7wfHcXbvGkEQBOEySGYJghgZkiSh0Wig0Wig2WxCEAT4fM8uEHEcB7/fL//x+Xzw+XzgOI5ElyAIglCFkyRJz/113ZkgCAIARFFEs9lEo9EA0JJWURRRr9dlmWXHIkmS0Hlc4jhOrt4GAgGSXIIgCO+j+eBOlVmCICxDFEW5Cgugr3yy29X+XZIkWYgFQWj7GZJcgiCI8YYqswRBmAqrrNbrdYiiCEBdYnmeB8/zSCQSCASMfa9m25IkCWtra5iensbU1BQAtLUrsJYFklyCIAjXQJVZgiBGi1aJLZVKSKfTKJVKiEajqFQqaDabCIfDiMfjiMViiMfjiMfjAyVX+fhsm36/v62SK0lS2z74fD4EAoG2nlwmugRBEIT7IJklCGIomDhms1lwHIfJyUlVic3n80ilUmg0GlhcXMTMzIzcMytJEgRBkKu1Ozs74HkezWYToVCoS3KDwWDXfnAcJ/fa9qrAMuEWBEFVcnstPiMIgiCcC8ksQRCGkCRJXtQlSRJyuRwCgYB8mZ/d5/j4GKlUCj6fD0tLS5iengbwrJIKtOQzHA4jHA5jdna27efr9bosuXt7e+B5Ho1GA8FgsE1yRVHsWjjWySDJrdfrEASBJJcgCMJFUM8sQRC66JRYJojr6+vgOA7nzp2DJEk4ODhAOp1GJBLB0tISJiYm2h5HFMWu0Vx6EAQB5XJZFt1sNgsAiEQicgWXiW4oFDIkn/0mLJDkEgRBWIrmgynJLEEQmmAzYpV9qEpx29jYgCiKCIVCyGQymJycxOLiImKxmOrjDSuznaTTaSQSCUxPT7dJLs/zEAQBfr+/S3LD4bApkqtsWWCzcpXTFSgQgiAIQje0AIwgCHNQBh0Az8ZhKRFFEblcDtlsFqdOncKdO3cQiURGup+sZzYYDGJqaqqt3QEAGo2GLLnHx8fY3NxErVaDz+eTJZeJbiQS6SufvcaIMcntrFxLktS3kkuiSxAEYRyqzBIEoYpa0EGndDUaDWxsbGB7exuxWAwTExNYWVnR/PhmVmYzmQyi0SgWFhZ0/Vyz2eyq5FarVfh8vrZFZ7FYDNFo1PR2BfbloHPCAkkuQRBjDlVmCYIwhpagA0EQsL6+jr29PZw+fRoPHz7EwcEBKpWKHbsMoH2agR78fj8mJia6enqbzSYqlQp4nkehUMDOzg6q1SoAqEpuPykfVMkVRRG1Wq3rZygQgiAIYjAkswRBaJ4RW61WkclkcHh4iPPnz2N1dVWWODZiSw9mSpnZguf3+5FIJJBIJNpuF0UR5XIZ5XIZpVIJe3t7ssRHo9G2lgWjkgu0p57t7++D53mcOXNG3jcKhCAIgmhBMksQYwwTpkaj0Vdiy+Uy0uk0CoUCLl68iMuXL3dJGsdxbeO2Ro3RyqxefD5fT8mtVCpyy8LBwQHK5TKA9gkLTHL9fn/f7ShfB9a3PCgQQq0nlyYsEAThdUhmCWIM6ZRYJk6d0lMsFpFKpVCtVrG4uIjr16/3FKNRyWQ/7Ny+ciHZyZMn2/ZJKbmHh4col8sQRbFLcmOxmC7JVTIo9YzGiBEE4VVIZglijOg1I7ZTanK5HFKpFERRxNLSEmZmZgaKj5E2g07pGganihnHcYjFYojFYpibm5NvlyQJ1WoVPM+jXC7j+PgYPM9DFEU52pf9aTabA58fBUIQBDGukMwSxBigJrGdbQKSJOHw8BDpdBqBQADLy8td4636obfNwOweTydUhvXAcRyi0Sii0Wjb7ZIkoVaryZK7vb2NXC6HRqOBfD7fVclVi/bt3E4vyQVaEynq9Xrbv5HkEgThJkhmCcLDqAUdqEns/v4+0uk04vE4rl271tUPqgW7ZdLunl2z4DgOkUgEkUgEJ06cAAAcHBygWCzizJkzsuTu7u52Rfsq/2iRXOV/GYMkt9cYMYIgCLsgmSUIDyJJkrzafnJysmfQwc7ODtbW1jA9PY1bt251VQn1YKTNgNAOx3EIh8MIh8OYnZ1t+zdBEOQZuWzyQb1eRyAQUJVcCoQgCMJLkMwShIdQBh0Ui0VsbW3h5s2bbfdpNpvY2trCxsYGTp48ibt37yIcDg+9bSOVUbN7ZsdVpkOhEEKhEGZmZtpur9frsuRms1msra11RfuyP6FQyBTJ7fwZCoQgCMJqSGYJwgOoBR0EAoE2uWw0GlhfX8f29jZOnTqFBw8eDLwUrQcjMjnOPbOjIBgMYnp6GtPT0223NxoNWXIPDw+xsbGBWq0Gv9/fFggRj8cRDoeHklwKhCAIwmpIZgnCpQwKOmByJwgCMpkMDg4OcPbsWayurg4c/2QEn89ne88qyaw2AoEApqamuhb4NRoNeYTY8fExtra2VKN94/E4IpGIIckF2seICYKASqWC4+NjnD59mgIhCILQDcksQbgMrUEHgiAgn8/jtdde60rrsgK7K6Nel51RPL9AIIDJyUlMTk623d5sNmXJzefz2NnZQaVSgc/nU0090ztGTBRF8DwvfyFiVxiAZ60oFAhBEEQvSGYJwiVoDTrgeR6pVArFYhGBQACrq6sjOeE7QWa9Wpm1+3n5/X5MTExgYmKi7XYW7cvzPIrFInZ3d1GtVgHoi/btN/OY/TsFQhAE0QuSWYJwOFqDDgqFAlKpFARBwNLSEi5fvoy33357ZCd1u6cZeFlmncqgaF/lhIVKpQJJkrokNxaLDVwISIEQBEH0g2SWIByKlqADADg6OkI6nQYAOa0LQFsbwihwwpxXkllnoIz2VSKKopx6xiYsVCoVeZ5tMpk0LdoXoEAIghgXSGYJwmFoDTrIZrNIpVIIh8O4dOlSV5/jqCuldldGSUacD1tIFovFcPLkSfn2w8NDHBwcYGpqCjzP4+joCOVyGaIoIhKJtC0+i8ViCAT6n7ooEIIgxguSWYJwCExi2azOXhK7u7uLTCaDiYkJ3Lx5s6v6xRh1pZTaDIhhCAaDmJubw9zcnHybMtqX53lsbW2hXC6j2WwiHA53TVgYVnL7BUIoR4jRhAWCcBYkswRhM8qgA0D90qkoitje3sb6+jpmZ2dx584dRCKRvo876hMttRkQRunVM6sW7cvur0w929nZAc/zaDabCIVCcgXXrGjfXoEQlHpGEM6AZJYgbEIt6KDzJNhoNLC5uYmtrS3Mz8/j3r17CIVCduzuQOyujJJAuBe9SXC9on3ZYjAmuXt7e+B5Ho1GA8FgsEtyB32Whkk9o0AIghgdJLMEMUIGBR0w6vU61tfXsbOzgzNnzuDhw4cDL6Hajd0nartl2mrs/v1aiVmxxhzH9Yz2FQRBHiN2cHCATCaDer2OQCDQ1o87TLQvey7KQAgGm7gwMzNDgRAEYTLOPjsShEfQGnRQq9WQyWSQzWZx7tw5y9K6vIiXZdarz4thlsz2g0luZ7RvvV6XJffw8BDr6+sQBAF+v79LcgdF+wK9JywUCgXs7++r9rh3tiv4/X6SXILQAcksQViIUmIfP36Ms2fPIpFIdJ2kyuUyMpkMcrkcLl68iEuXLlma1uUUzDxZe1lmvc4oZLYXwWBQU7Tv5uYmarVa29gxJrmDon2B1nNkwtp5OwVCEMRwkMwShAWozYhlJyzliahUKiGVSqFSqWBxcRHXrl2jExUxdtgps73QGu27vb2NarUqjx1Tiq4y2pel9nVCgRAEMTwkswRhIv2CDljuPADkcjmkUik0m00sLS1hdnZ2LE9EZkoMVWbdixNlthe9on2VklsoFLCzs4NKpQKO4xCLxQC0nifP832jfRlaJJcCIQiiBcksQZiAlqADn8+H4+NjJJNJBAIBLC8vd13atGrfxuFkRjLrXrzwHu0luaIoolwuY3t7GzzPI51Oo1KpAEBbtC8LkxhGcgFKPSPGE5JZghgCrUEH+/v72NnZQSwWw/Xr17uy7K2CCd64nLS8LLNefg1ZOIEX8fl8SCQSmJiYQDQaxblz5wC0JLdSqbRNWCiXy5AkqU1y4/E4otGopmhf5X8ZnZKrJRDCq68F4V1IZgnCAFqDDlha1/T0NE6dOoXJycmRiSzwrLXBqScnM2Xb67LnZcbhC1fn51C5kEwZ7StJEiqVijwr9/DwsC3aVym5sVhsaMmlQAjCC5DMEoQOtAQdNJtNbG1tYWNjA3Nzc7h79y7C4TDW1tbknxsVyj5dp2H2SZHaDNzLuMisllnRrMc2Fot1SW61WgXP8yiXyzg+PgbP8xBFEeFwuEtyzYr27fwZCoQgnAjJLEEMQGvQQaPRwMbGBra2tnDq1Ck8ePCgLUbTDrF0ssxaAcmsO3Hy1QOzGPY5chyHaDSKaDTadrskSajVarLkst5cZbSvUnKNRvuybakFQgDts3IpEIIYNSSzBNEDrUEHgiBgbW0N+/v7OHPmDB49eqRaFfH5fF0LM6zGDpm1q8pGJ03CyVgl7BzHIRKJIBKJ4MSJE/LtkiRBEAS5XWF3d7cr2lf5Z5Dksm0NktxsNot6vY5Tp04BoEAIYjSQzBJEB50Syw68nQffarWKdDqN4+NjnD9/Hqurq31PVn6/H7Vazerdb4PNtx3l9uyUWarMupNxaTMYZfWZ4ziEw2GEw2HMzs62/ZtScvf398HzfFe0r1Jy9aSesVYqv98/MBCCtSrQhAViWEhmCeJHqM2IVZNYNl6nWCxicXERV69e1XQA9vl8tvTMjlLwRr09JSSz7mVcZNYpz5FF+87MzLTdXq/XZcnNZrPIZDKo1+tt0b7sTygUUn0+zWZTvjI1aFauIAiUekaYAsksMfb0CzpQUigUkEqlIAgCFhcXcePGDV0H2HHomWWV4EErrK3aNuFOxkVm7fhc6CEYDGJ6ehrT09NttzcajbbpChsbG6jVavD7/W2pZ/F4HI1GA+FwuO92KPWMMBuSWWJs0RJ0AADHx8dIpVIAgMXFxa5Ldlrx+/1jIbNaq6PFYhGZTAZ+vx+JRELzqKF+eLky6+WT9rjIrFufYyAQwNTUVFfIS6PRkOfkHh8fY2trC/l8HsFgENlstk1yI5GIrnYFJRQIQQyCZJYYO1ikJJPXXkEH2WwW6XQaoVAIly5d6spo14tdbQajlFktbQaFQgHJZBKNRgPnzp2DKIrgeR5HR0fyPM3OofFak5G8KrNefV6McZBZLwZDBAIBTE5Oth0bnzx5gtnZWYRCIfA8j3w+j+3tbVSrVXnsWGcghBbJVf6X0SsQgt2XAiHGB5JZYmxQBh28++67WFlZ6QowkCQJe3t7SKfTmJiYwI0bNxCPx03Zvh1tBnYsAOu1vXw+j2QyCUmSsLS0hJmZGXnc2dzcnHy/zqHx2WwW5XIZQHv8ZyKRaDsRKmX2mwv38eN737f42RJm4UXR62Qcxo8BrZ7ZYDDYN9qX53kUi0Xs7u6iWq0CgGrqmZYvsMr/MigQYvwgmSU8j1rQQeclf1EUsb29jfX1dczMzOD27dtd8xyHxa6e2VFW9dSqo7lcDslkEhzHYXl5uetSpdpjqA2NZ/GfTHL39vZQqVTk+0ejUZQ+8r/hm5Y8M8JKxqEyO04y26tViEX7dhYROj/b+/v7qFQqqtG+Wq/SKP/LoEAI70IyS3iSQUEHfr8fzWYTzWYTm5ub2NzcxPz8PO7du4dQKGTJPrFtjhK7FoABrV7jp0+fIhAImNamwU5oSkRRxLdPPey6/2uvvYZYLCb348bjcYTDYToxORA395NqZZxkVu/z7PfZZqlnyqs0THKVLQvDRPsC2gIhSHKdC8ks4Sm0Bh0AwObmJvL5PE6fPo2HDx9qipochnGZZpDL5fD48WMEg0FcvXq161KjWXxz4X7ff6+89Ku48vRfUCqVcHx8jM3NTXkFtrLSk0gkNM3SJKyDKrPeoV9lVi8+n29gtG9nv30kEumSXK0xwnolVxAEhMNhRCIRCoSwGZJZwhOw8VrNZrNv0EGtVkMmk8Hu7i4WFhawuro6snE5XpZZSZJweHiIw8ND1Ot1XLt2retSolkMklglan17nWOG1tbWVAfGM8klrIdk1juMYgSZMtq3s9+eRfvyPI+trS2Uy2U0m02Ew+GuxWfDSu76+jpOnjyJyclJCoSwGZJZwtVoDTqoVCpIp9PI5XK4cOECLly4MPQYKL14cQEYm/qQSqUQjUYxOzuLxcVFS0RWj8T2o9eYIeXA+IODA6TT6bboT2W7gtVVfDXoROhuxkHYAXulXWu0787ODnieR7PZRCgUkiu4eqN92c8rjwcUCGEPJLOEK9EadFAqlZBKpVAul7G4uIhr166B4zisra15Po2LbdOK5ylJEg4ODpBKpZBIJPD8888jFovhvffeM12ezZLYQfQaGM9OgqVSqe0kGA6Hu1KRrPpyRKO5vME4PEfAec+zV7QvW1ehXFTK83zbl1il5Haup2g0Gl1fbM0IhDg+Psb8/LzJvwVvQzJLuAqtQQf5fB6pVAqNRgNLS0uYnZ1tO3jYsRjLDnw+X9eQ8WGQJAn7+/tIpVKYnJzECy+8gFgsJv+73lmv/U56o5LYQahFf7LKS6lUki9n8jwv9+x1Su44XF4ehnGR2XHATV+8OI7rGe0rCII8Ruzg4ECO9mXtSLFYDJVKpe1cNGhbWgMhPvzhD+ONN96gz4QOSGYJV8Aklo1T6RV0wNK6fD4flpaWuqpsDLMlz6mY1dqgnL87NTXVc3SZGdVnMyXWqnmzykpP5+XMzoUpPM+3jRhi7Qpa5miOC+MwZ5ZwF0xyO88h9XpdllxBEPDkyRMIgtC2sJRVc7VMT+mcsMCOnySy+iCZJRyNMugAUP92yy55p9NpRCIRXLlyZeAK+nGqzA4js5IkYWdnB5lMBjMzM7hz5w4ikUjP+w/To+uUSuww9FuYwuZolkoleY4mAFXJHbcTGVVmvYGbqrJGCQaDcs/95uYmbt++DaA72pdNT1GOHWOS2y/adxzG1FkBySzhSNSCDjo/4KIoYnd3F2tra5icnJT7NrUwLjJrVC5FUcTOzg7W1tYwOzuLu3fvIhwOa9qe3hPat557oHv/3IaWIAiWiMSCIJRtCqzy41XoBO4NxrnCrhbtC7RGlTHJVUb7KseOxeNxlEolnDt3DqVSydRxho8ePZILEH6/H9/4xjdMe2wnQTJLOIZBQQcMURSxtbWF9fV1zM3NDawWqjEuMqv3sj9LQltbW8Pc3JzuEAk92/vGzC3Nj+tVlFUb5YKPzhMgG3m2t7fXNT4sFAq5XgSpMusNzJwx6xX8fr/qiEDlZ7xYLOJ3fud38N5774HjODQaDfz+7/8+rl+/juvXr2N5ednwBJWPfOQj+N3f/V0TnomzIZklbEdr0EGj0cDGxga2t7exsLCA+/fvG07rsktmWaV0VNULrW0Gyi8I8/Pzhn+3WivBJLL96TwBRqNRiKKIU6dOyf24vYIgWLuCVUl2VuB1mR2Hy+/AeMnssMfxzs/4l7/8ZQDA97//ffzZn/0ZLl++jLfffht/+7d/i2QyCUmS8LWvfQ2nTp3StZ133nkHn/vc51CpVHD//n289NJLhvfZyZDMErbBqrCNRqNtPmznSU0QBKyvr2N3dxdnz541Ja3LqpFVWrbrJJltNpvY2trCxsYGFhYW8ODBg6GCAga1GdghsVYtAhs1HMfB7/erXspUBkF0rrxWzsfVOkNz1HhdZsclMMFIlK1bURvLZQaVSgXnzp3Dz//8z3dtz8jv9jd+4zfw4MEDNJtNfOhDH8LExAQ+9KEPmbW7joFklhg5yhmxm5ubEEUR58+f7zqZVatVZDIZHB4e4vz58/jABz5g2oHS7/ePPMAAGH1wQq/tNZtNbGxsYGtrC88995xpcb69ZJYqscMxqLLXLwiCjQ/rnKHZKbl2BEEwSGa9wSjSv5yCVTKbz+dVp/AY3daDB601CX6/Hz/+4z+Of/3XfyWZJYhhUAs6CAaDKJfLbSeycrmMdDqNQqGAixcv4vLly6afCOxqMxi1RHfKLGvV2NrawunTp02T2F7bI4m1l2AwiJmZma4ZuUrJ7RUEkUgkRp6S51XGRWbHqc3AqudaKBR6jpTUy/vvv49vf/vb+NSnPgUAePLkCT72sY+Z8thOg2SWsJx+M2KVUlksFpFKpVCtVrG4uIjr169bVq2xS2ZH3d7AKqWNRgPr6+vY3t7GmTNn8OjRI0uqCmx7JLHOhQ2Kn52d7UpDUubab2xsoFwutwVBsGpuLBYzXc6oMut+xklmrarM5nK5toknwzA5OYmvfe1r2N7eRqFQwLlz5/DJT37SlMd2GiSzhGWoSWznCcvv94Pnebz++uuQJAlLS0uYmZmx/MQ26sv9dm1XFEUUi0W8+uqrOHPmDFZXVy072ZDAupt+ufYsCKJUKiGbzaJcLkOSpLaoTwqC6M24jB4jmR2eQqGAlZUVUx7r9OnT+OpXv2rKYzkdklnCdLQGHRweHsrpKbdv3+7q97MSu04so5LZer2OTCaDvb09cByHR48ejbXEemURmB30CoIQRRHValVuV1AGQahJ7jjIXC/GZf4qyezw5PP5rmhdYjAks4RpaAk6kCQJ+/v7SKfTiMfjWFlZwdbW1khF1k6sbm8QBAGZTAYHBwc4f/48Hjx4gDfeeMOSE4wbJJawDuXQdyWiKLbNz2RBEOz+ynYFLXGfXmCc2gzG4XkC1vbMjsv50ExIZomh0BN0wBKlpqencevWLUSjUVSr1bEIL2BYVZkVBAHpdBrZbBYXLlzA6uqqvC2zt0cSS/TD5/MhkUggkUi03a4cEp/L5dpm5FarVWxsbMiVXC8EQSgZF5kVRdFV842HodFoaE6c1ANVZo1BMksYQmvQQbPZxObmJjY3N3Hy5MmuWNRAIEAyOwS1Wg3pdBpHR0e4cOECLl261HbSNBIv2wuSWHtxu9z1SkJqNBp47bXX4Pf7cXh4iPX1dQiCgEAg0Naq4LYgCCXjIrPUZjA8vUZzEf0hmSV0wcZrNZtNeVGDmsTW63U5rev06dM9h/HbHSs76vmWZo3mqlarSKfTOD4+xsWLF3HlyhXV52HGc/OKxLq5b9bLc1gDgQD8fj9Onz7ddnu9Xke5XEapVGoLgggGg11pZ3bOyNUCyaz3sEpmi8UitRkYwNlHAMIxqM2I7ZXWxXo2z549O3D1vJmVQ70wsRzlwXfY0VyVSgXpdBr5fB6Li4u4evWqZZLjFYkl3EkwGFQNghAEQR4ftru7KwdBhEKhLsl1iliRzHoPq57rOAVPmAnJLNEXNYlVOyhXKhVkMhkcHx/jwoULWFlZcfzBm4nlqGXWSGW2XC4jlUqhWCxiaWkJ165dI4klxpJQKIRQKNQVBKGU3K2tLZTLZTkIQpl2ZkcQxDjJ7Dg8T8CayqxdhR0vQDJLqNIv6EBJqVRCOp0Gz/O4ePGipZVCs7GjxcHn88m/Uy2Uy2Ukk0nwPI+lpSXcuHGDJJYgOuA4DuFwGOFwuGcQRKlUwtHRkRwEEY1G2/pxrQiCYIyLzI5TVdEqmVW74kkMhmSWaENL0AHQGh+SSqUgCAKWlpZw4sQJ130A7ZBZv98PQRAG3q9UKiGVSqFSqWBpaQlzc3MksQShk35BEJVKRa7ksiAIAG2Sm0gkTJmROy4yO25tBma/pjzPIx6Pm/qY4wLJLAFAW9ABABwdHSGVSoHjODmta1g4jrPlYG9XZbZfm0GpVEIymUStVsPy8jJmZ2dJYk3EzYvACPPgOE6ekauMDhVFsU1y1YIgWMtCJBLR/Nkcl4rlOMksYP6EkVwuR4u/DEIyO+aw8Vrvv/++3OeqFnSQzWaRSqUQiURw5cqVrvE6w8DGc9khs6OOtO0ls8ViEclkEvV6XZZYqxhHiSWci5P6BH0+n1yVVaIMgsjn89je3ka1WpWDIJQ9uWpBEFSZJbSQz+dJZg1CMjuGqAUdHB8fd43/kSQJu7u7yGQymJiYwM2bNy25BOL3+9FoNFRHd1nJsJMFjNBZDS4UCkgmk2g2m1heXrZsWLYkSfiX2duWPLab+OBnP2r3LhjCy6O53PDclEEQCwsL8u0sCKJUKuH4+LgtCELZj9toNBz/HM3ADa+lGVj1BSyXy9GMWYOQzI4R/YIOgsGg3NAuiiK2t7exvr6O2dlZ3LlzB5FIxLL9smvWrJ1tBvl8Hk+fPgUALC8vW3oAq7z0q/gXyx7dHbhVYscBNwtQvyAI1qpweHiIg4MD7O/vY3Nzs01yE4nEyL/EE8NjVQWaAhOMQzI7BmiZEcuel0HFAAAgAElEQVQWJu3u7mJzcxMLCwu4d+/eSBJ37EoBs0NmWR9erVbDysqKpZeUqJ1AXWKlv/gdcJ/6P23YG0INN8tsLwKBQNeM3Lm5OSQSCVlyDw4OkE6n5atSyn5cNwRBjDPNZpPSvxwGfVo8jNagA5a08+abb+LcuXN49OjRSA+krM1g1IxSZo+OjpBMJgEAiUQCL774omXbIomlSqyb8KLMdsJ6ZoPBIKanp7uERTkjd2dnBzzPyzNyOyN9qSfVfqxK/yoUCtQzaxCSWQ/Cxms1m82+QQe1Wg2ZTAbZbBahUAiXLl1qW9k7KuxqM9A781UvkiTJEhsKhXD16lUEAgE8fvzYku2RxJLEupFxktle9AuCKJVKchAEz/MQRRGRSKRLcu1eYDYOryPDKpnN5/O4cOGC6Y87DpDMegitQQflchnpdBqFQgEXLlzApUuXkEqlRr6yn2Fnm4GWma96kSQJh4eHSCaTiEajuH79OhKJBIDWFwizf88ksfollloNnMM4SJCRaQbKIIjOGbnValWu5KoFQbB2hWg0OjLJHbf0L+qZdRYksx5Aa9BBsVhEOp1GpVLB4uIirl+/Lt8vEAjYcqkf8E6bgXKEWSwWU53+YOY4MJJYqsR6AZJZfXAch2g0img0irm5Ofn2ziAI5YxcNck1+3c+LrN0Aet6ZguFAsmsQUhmXYzWoINcLidXXhcXF1UH8dsts/V63ZbtmiGzkiTh4OAAqVQKiUQCzz//PGKxmOp9zRgHRhJrjsS6rTrrVeEjmTUHLUEQxWIRu7u7qFQq4Diuq1VBTxBEJ+M0Y9bKNgOrxjN6HZJZF8LGazEpUpNY1q+ZSqUQCASwvLzct7E8EAigVqtZut/9tl2tVke+3WFlVpIk7O3tIZ1OY3JyErdu3UI0Gu37MxzHGZ5RSBI7vpVYJwULmA3JrLUogyDm5+fb9onNyO0MgugcHxYKhQa+RuMms1ZM+qE2A+OQzLoEtaCDXhK7v7+PdDqNWCyGa9euyf2a/bBrERbbtpvaDJRhElNTU7h9+/ZAiWUYOWmTxI6vxI4D4yKzTnuOyiAIJc1mU25V6BUEwdoVlEI3bjKr9ZivB5pmYBySWYfTL+hAiSiKsmBNT0/jhRde6HmpWw272wzsmmagp39V+TuemZmxPEyCJLaFlSLrtlYDLzIOMitJkmsWR/n9fkxOTmJycrLtdmUQRDabRSaTQb1eRyAQkIW4Xq+jXq97PgjCqp7ZZrPp+d+dVZDMOhStM2KbzSa2trawsbGBubk53L17F+FwWPf27JRZp4cmiKKInZ0drK2t4cSJE4Z/x1ohiW1B1djxgGTWHagFQQAtgeV5Xu7Ffeedd+QgCGUIhJeCIKzomfVyK9Eo8MY7y0NoldhGo4GNjQ1sbW3h1KlTePDgwVDf6MaxMjtouyzWd21tDSdPnrQ8EY0ktgVJ7HgxDjLrZVgQRLVaRTQaxYULF+SWODYjt1cQRCKRQCwWc117gpUyS58FY5DMOgStQQeCIGBtbQ37+/s4c+YMVldXTTkQ2C2zTuqZFUURm5ub2NjYwPz8PO7fv08SOwLsklhqNbAXkllvoBzNxXEcQqEQZmdnMTs7K99HkiTUajW5XWFzc7MrCIJVc2OxmGOr2VbMma1UKrpaA4l2SGZtRjkj9rXXXsP9+/dVP8DVahXpdBrHx8c4f/48VldXTf2g2yWUbNt2VGY7Jws0m01sbm5ic3MTCwsLQ1e7+yFJEv5l9rYlj+02nFCJtXO1+bhDMusNtPSRchyHSCSCSCTSMwiiVCohm82iXC4DeDYjl/0ZZRBEL6zomc3lcrT4awhIZm1CLeig0Wh0HdR5nkc6nUaxWMTi4iKuXr1qyYHfzoODnTILtA5MGxsb2NzcxKlTp/Dw4UNLe7sqL/0q/sWyR3cPP/4HL8l/t7tf7PXXXwcAxGKxturQMHM3zcYp+2E2JLPegLUQGKFXEIQoim2SqwyCYJ9VpeSO6n1kxZdfGss1HCSzI2ZQ0AE7sBcKBaRSKQiCgMXFRdy4ccOzB3y7nlej0UCtVsMrr7yCM2fO4NGjR5ZKLLUTtFBKrFN4FMiifuunUC6XwfN829xNNpKICW4ikRj5imO7Zd9KSGa9gRVxtj6fr2cQBPusKoMg2P2Vn9dwOOyK91ehUOiaIEFoh2R2RGgJOvD7/Tg8PMTa2hoAYGlpidJALKDRaGB9fR07OzsAYFrfcS9IYls4UWKVKOduLiwsyLezkUSlUgkHBwdIp9Py0HSl4LpxIYsTIJn1BqOMs+03I5dJbi6Xw9bWlvyFNBaLtU1X0BIEMUpyuRxVZoeAZNZC9AQdZLNZlEolrK2t4dKlS7Z9Q/PyiaVer2N9fR27u7s4e/YsHj16hFdffdWyAzBJbAstEjtMMtowBF58JP/d/8b/i+ad/9Z9H5WRRJIkQRAEebX2xsYGyuUyRFHsqgyN8vKnG/HyMQdwZmCCFTghNMHv92NiYgITExNttzcaDVlyDw8Psb6+DkEQEAgEuiJ9By32ter1pDaD4SCZtQCtQQfKONSJiQnMzMzg0qVLXR/EUcEmGtg1tNmqk5pyAsS5c+faFs9xHGd6/xNJbAsnV2KVEmsEjuMQDocRDoe7FrJUKhWUSqWuy5+drQpWTshwEySz3sAJMtuLQCCgGgRRr9flSN+DgwM5CCIYDHalnbEWNKsCE0hmh4Nk1gLYwq5eM2LZ/NL19fW2JKnHjx+jXq/btNf2yixL4zLzYCgIAjKZDA4ODnpOgGDbNUNmSWJbeFliB8FxnNzjNz8/L9/OIkJLpZLcSsROmkrBjcfjjhUCq/C6zHohMEELTpbZXgSDQdUgCEEQ5PFhu7u74Hlebi0Kh8NoNBooFAqmfl7z+TzOnDljymONIySzFtBrRixbNb+1tYX5+fmuIfx2znq1e/ssBcyMA0OtVkMmk0E2m8WFCxf6jjFjkxSG+ab99cQL4ILePRlrZViJtbLVQKvE9mo1GJZeEaHspFkqlbC1tdU2c5P1BMbjcU8Ln5efGzA+Y9/cKLO9CIVCCIVCbWtWWGsRawnc2tpCuVyWpzgo+3GN9M9TZXY4SGYtwOfztY2aYr2aOzs7OHPmTM/RT06QWTtGZAHP5twOc+m1Wq0ik8ng6OgIFy9exKVLlwaeRIYZC/b1xAuGfs5rjHMldlh6nTSr1SpKpZI8jiiXy8Hv9yObzXa1KrhdBElmvYEV0wycBGstisfjmJqawuXLlwG0B0GUSiUcHR3J/fOdM3L7BUEUCgWaMzsEJLMWoqwQsl7Nft/WgsGgrW0Gbg1OqFarSKVSyOVyWFxcxJUrVzSfHI1slyS2hVcl1qrqrFaUMzfZOKJMJiMnJPE8j+PjY2xubqJWq8mLWJSVXCtHzJkNyaw3GJfn2Rll2y8IolKpyO0KakEQpVIJAHDt2jXTK7OVSgUPHz7Ehz/8YfzxH/+xaY/rVNxzxHMRgiDg8ePHyOVymiuEQKsyWqvVRrCHvbdvd5uBHiqVClKpFAqFAhYXF3Ht2jXdJ0W/3y8v0hsESewzrBLZYVsNnF6JHQafz6e6Urter8tVod3dXZRKpa5Ln2x0mBNlg2TWO3j5dWR0ymwvlP3znTNymeS+/vrr+Ku/+itsbm6iVCrh5Zdfxv3793Hjxg3cvHkTFy5cMPzeefnll3Hnzh1DP+tGSGYtwO/348SJE7rlyu7KrJ0yq6cqXC6XkUqlUCwWsbS0hOvXrxs+iHa2hKihRWKlujQWfbNOrcaaLbF2V2f1EAwGMT093VbVYZc+2eiww8NDuSrktJQzkllv4OXXUMmwvcFsskk8HscnPvEJfOITnwAA/MRP/AR+8zd/E0+ePMH3vvc9fOlLX8La2hp+7dd+DZ/61Kd0bePLX/4yfuzHfgxvv/22XP31OiSzFhAIBNqGruv5Obt7Zu2SaS2X+3meRyqVAs/zWF5eNiUVrd92qRL7jHGRWK+gvPTZGQ/qtJQzr6/2HxeZHRcajQYikYjpj9tsNvHiiy/i7t27bbfrvVL13nvv4fHjx/jsZz+Lt99+28xddDQksxZgVLCcILMs99qObfeSylKphFQqhUqlguXlZZw4ccK0KoCazJLEPsMOidXaamC1yLqpOqsVJ6acUWXW/Xg5brkTrW0Geuj3+9P72fjqV7+KSCSCP/zDP8S3vvUtCIKAP/3TP8VnPvOZYXfT0ZDMWoSR3j9qM2jfdrFYRDKZhCAIWF5exuzsrOknPaXMksQ+w6mVWICqsVZgZ8rZOMisl58f4P3XUIkVMguoBysZ4bd+67fkv7OpKF4XWYBk1lE4oTJr52gutvitUCggmUyi0WjIEmvldh9f+W94bNkW3AVJbDvF7TQmTi+OfLud2CEL/VLOWKuCGSlnXhchr7dRAN6aMTsIK55rtVo1PRHwH/7hH/Bv//ZvEAQBf/M3f4NPfvKTpj6+0yCZdRA+n8/WyzV2juYKBAI4OjrCD37wA4iiiOXl5bbZm1ZgdiXWzYvAnCaxyisbdlVicwtXbdmu0+E4Tl7AYkbKmddl1uvzV4HxklkrKrP5fN70GbMf//jH8fGPf9zUx3QyJLMWYWWakVXYVRnO5XJyO8GtW7csT0GhdoJnOE1ilThFYp1SnXU6/VLOWKuCMuWMzdosl8vyiDwvSh9VZr2FVTJL6V/DQTJLyIxaZo+Pj5FMJuHz+XD+/HnkcjlLP9Aksc9wssT67zy0Zbv9KrEktMYJhUKYnZ1taxdSppzlcjns7+9jd3cXAFRbFdxcufWqpCsZh+ozwwpxt6IyO26QzFrEsHNP7fiWO0wKlx6Ojo6QTCYRCARw+fJlTE5OypcmrYAk9hkksd1QO8HoUaacFQoFTE9P48SJE2g2myiXyyiVSjg+PsbGxgYEQUAgEOhqVXBLypkoiq7ZV6OMU2XWirYYqws544C3P2EuhFVH7TgwWFn9kCRJlthwOIyrV6+2JRlZIdJ2SKxT+2ZJYrvRK7FUnbUGpRz4/X7PpZyNQ2VWFMWxkVkroDaD4SGZtQijYsjGc4XDYZP3yB4kScLh4SGSySSi0SiuX7+ORCLRdT8zF59RJfYZJLHdOLUSu75XwvmF7s+G19FS6RqUcsau7KilnCUSCYTDYdtaFcZBZsepMmsF1GYwPCSzDsPu8VxmIUkSDg4OkEqlEI/HcfPmTcTj8Z73N2MsGEnsM0hi2zFLYK2qzu7sHwMIYn2vFT2pJrVu7hvth9HLtoNSzkqlkiNSzkhmvYNVvcGFQgErKyumP+44QTLrMOyMlAVaJ4hhDr6SJGF/fx+pVAoTExN44YUXEIvFNG/XKCSyLUhiuzG7Emu20O7sH6MutUtVZ5XWbZNR9GB2D6Iy5UyJ1pSzeDxuqrCMi8x6/TkCredpRf8ztRkMD8msRQzTZmB3cAI7wOtBkiTs7e0hnU5jamoKt2/fRjQa1fzzXqo62dE3SxLbjZXtBBt7RZxbmBh8xwGoiSxjXNoORjVnVk/KmSRJ8uiwYVPOxkFmRVE0fei/E7Eq/YtkdnhIZh2G3ZVZvTIrSRJ2d3eRTqcxMzODO3fuIBKJWLyX3fzX0ttjW511qsh6UWJz/meXs4cV2n4iyxgHobUzNGEUKWfjEGc7Lm0GVi3OJpkdHpJZiximMlupVEzeG+1o7dkVRRG7u7vIZDKYnZ3Fiy++aIvEjjMksd1YJbJKiVViVGhbPbLaWN8rQYhcAKD9Z9yEExPAzEw5o9AE72BlZdbqxEuvQzLrMOxeADZo+6IoYnt7G+vr6zhx4gTu3r1r6uQFJ57YnAZJbDejllgleoWWieygqiyj3Gy162SFGQzeG/fhps+8kZQznudxfNx6zWOxmGueqx7GRWat6plls5YJ45DMOgyntBl0Iooitra2sL6+jpMnT+LevXum90ixWbNeHzBuFKdKLOC9lgItEqtEi9Aqq7FaRbaT97dbEz+unvaOOLhJZnvRK+WsUqng3XffRbVaRTqdRrlchs/nQywW81TK2bjIrFWV2VqtpmuNCdENWYNFuHkBmHJEliiK2NzcxMbGBubn53H//n3LGv2ZSBs9WDipb9bMRWAksd04RWIBoCq2rkw82REAAJdOtX8+0rsVRHxV+f/1iCyrynby/nbTM0LrBZlVg+M4xGIxBAIBXLhwQR4D5sWUs3GZZmBFz6yXJ5WMEnd8UlwKx3G636h2txmw8IJms4nNzU1sbm7iueeew4MHDyyfyTiqOF238MHPftSxJ3mS2BZMZJUwqQWAhJ9HxOA5vpfIAkCtGcRbG62/3zpnfKSdE/CqzDI6pxn0SzljrQo7OzvgeR7NZhORSKRNcJ2acjYulVmrAo28/BkYBSSzDoMlgNmFz+fD3t4e1tbWcPr0aTx8+HBk1QEzghO8wAc/+1G7d6EnJLEt1CRWScLPq95utL1ASa3Z/hhvbbTExq1SO24y24tgMIiZmZm2hUCdKWfZbNaRKWfj0mZgRRucIAgjCe/wOiSzFmKkMuvz+YYKDzBKo9HAxsYG1tbWEI/H8ejRo5Ff4hr3yqyjJfbFR4ANl8NGNWZLK0YlFjCnvaAfb234XCm0XpdZwHjVTWvK2dbWFmq1Gvx+f1erwihEaVxk1oqeWYqyNQeSWYcx6oN6o9HA2toadnd3cebMGdy4cQPZbNaWXi3W4jAMbuyb7Sexdp/o/S8+smW7XpJYwDyR7azKdvJqutWv+3BR6Hs/J2H3e9yNaEk529/fR6lUki+Ns1FjVqScAeNxmdyKnlmaMWsOJLMW4uQPd71ex9raGvb29nD27Fk8evQIfr8fhULBtp7dcavMOr4S2wnHWV6d9ZrE6mUYka02nh3OX02HbBXadza7b3v+rPp9SWbNY5iUs0QigUgkQq9FH6xoMygUCl2j3gj9kMw6EI7jLItAFAQBa2tr2N/fx7lz57C6utq2HTsXoNm9+G1UuE5iR4ST+mIHSSwAlBsRlButoJD58GHP+1nRJ9uJUmQZdlVp1USW3S5Jz0TphXOtL0Yks9bSK+VMFEVUKhVTUs7GBSvaDHK5HFVmTYBk1oHojZTVgiAIyGQyODg4wIULF7okVrltu6qjXq/MGpXYUZzsNUusBdVZt0msKHV/bvZrJ1SF1uo+WS3YXaVlKEUWAN7e4H50O8msHTBpNSPlbFywYgQZpX+ZA8mshRg9QJsps7VaDZlMBoeHh7hw4QJWVlb6fhjN6Fs1it/vhyDYf9I1k9X/47/AH3VuzC9VYlvoldhqs/uz2Sm0o+qTVavKdvK//iOKn7hsfUx2r6psX+Ye4Qfrrb/eu+j9KzNOx0jKWa1Ww/7+vjw6zMtfTsx+brQAzBxIZh2IGeO5WOLM8fExLl68iMuXL2v6ENo1TQEwryrshEVgH/i9nzT18cyuXg0lsUNWZ62Q2Jx/DtPNrG6R1SKxwGCRZfSq0BrFDJGt1FvVs//1Hy1hHoXUdtJZle3Fa5nW8/GK1HppIH6vlLNSqYR3330XPM9jf38flUpFDozwUsqZVeTzeVy8eNHu3XA9JLMWMmxl1gjVahWpVAq5XA6Li4u4evWqrv2wdeW8jVXhYTFbXq3Ci5VY+fEtENnOloJ+IsvYr53ATKigeT+sai8AnomsEquqtL2qsv1EVmiqX6b2itR6vYWC4ziEQiFEo1EsLi7Kt3sx5cyq15KmGZiDO95FY4aRymylUkEqlUKhUMDi4iKuXbvmuoOo23pmtQpss1J1RKuB//Z9QGwCPhP63HRUZ902oQBQ74vVIrKMY2EShWoIFyazfe9nZXuBmsgyzK7SGmovGEBD9OG7qfbf+aMld7UhWbWQ10mo9ZF6MeXMqlm6hUKB2gxMgGTWgeipzJbLZaRSKZRKJSwtLeH69eumSKwdFQWnTzOwu/pq9DXx375vwd4MxisSa4RCtSVha4W5nkJrdZ/sIGoNH/75vTgA4KeumztijGGkKgu0RFYNpdy6QWzHQWb1RNn2SjmrVqvyorPOlDNlJdfOlDMrJhkAVJk1C5JZCxmmzWBQZZbneSSTSVQqFSwtLeHGjRumfchZhdTNCWBm9s1+8A8+AnHIHmY7qrM9Jdbi6qwXJVZPVZaJLKOf0KphZp9sz2002p/vP78XNyy0VlRltfDdVMjxQjsOMjtsxZLjOESjUUSj0bFMOaNpBuZAMutAgsGg/M20k1KphGQyiWq1iuXlZZw4ccL0b6psIZabZdYMPvgHH7F7FwxBldhnDBJZLZXYYUSW0Sm0o+6TVdIpsgyzq7RmV2XVYJVap0otyaxxtKSc7e3tgef5tpQzJrhmp5xZWZklmR0eklkLMXMBWLFYRDKZhCAIWF5exuzsrGWXW9hCrHBY20pvM7frFJm1QmTNqM72azXQJbEmVWfz85chcdadrI1KLKMpPXuOfu7Ze0trO4EZIstgQmtXn6xWWD9tJxPhOu5eaD8u2VWV7cSpVdpxkdlRPkctKWdHR0dtKWfKSq7RlDOrZLZSqSAWi5n+uOMGyazFcBynezyLcgFYoVBAMplEo9GQJdZq7Opd9fl8to+y6SWxvmBw6FYDq7CrEmslw0os3+w+OSjFlsPg95kekdXKuwcLWJxVn3Qwqj7ZfoQD7WP5JsLt7/nX19r3IeRXP06MoiqrpClx+Hay9eX7x5Zrhh7DCkRRdN1CXL1YVZnVg9aUs52dHVSr1baUMya6g+a6NxoN058nO995/T0yCkhmHUggEEClUsEPfvADSJKEpaWlkV6GcPpCLK3o7Zt1S1tB4PnbaLzz5vASO0R1Nn/ykvx3ThJNq84e+efhg/E5x2oS20m+1qo8TofVW3mMMKgqqyR91BpG30tqjWK0vYChFNlOiVWjl8j2o5/ImoWTpFaSJM9XZvUsABs1WlLOstksMplMW8qZslWBPTerWu84jiOZNQGSWYeRy+Xw5MkTlEol3Lt3z5aRHV6RWT2MSmSHbTUIvnAHgH3VWKXEmsmR/9mJRoRPt9BqkVjgmcgCQK4W6ym0ZrYXMEq19hN++mhSFlq72wvCAVGTwAKAj+v/2mgNSOhkmKqsGk6Q2nFpM3DLrFiGkZSzRqOBeDyOcrmMaDRqioA2Gg3Pvz9GhbvegS5Ea5vB8fExkskk/H4/Ll++jHfffde22XNekdlisTjwPnok1s5WAyaxDK5Zh+S3fgUvY5DEDlOdVYosQ6vQapVYoF1k+zEKkWWwKu3pqd7zXq1sL9AjscAzkQ341F8bo+0FRuklsoyG6MP/96T36/6fLlmbhjYuMjvq9RVW0SvlrFKpIJlMol6vI5VKdaWcKVsV9EhuoVDoEmrCGCSzNnN0dIRkMolgMIgrV650DZm2AztlluO4oU8ApVIJT58+HTjezK62Aq3V2U6BtYQBrQZ6KrF6hVZNYtt2rY/Q6pFYoLfIdlZnRymyAFCutX5fT/fjWJk3NkXASHvBXFxftVJZje0lssNgtCo77GN2iu5/ulRRlV9lPUJP0MS4yKxT2wzMgElrOBzGyZMn5ZY/ZcrZ0dER1tfXdaec0YxZ8yCZtRi1b2mSJMkSGw6Hce3ata7xI3YSCAQgCPasDGZjwYycANjYslqthpWVlda36x59s0ZF1urqrB6BtbI6a1U7ATBYYpWIaL0PlFJrlsgymNBaseCrH0xkGU/3W6OxlFI7bHuBmsgWeB8KfBRL84OlbFBLgRKnVWWNMEhkgd7THtQkd1xk1uvPEehupxgm5SybzWJlZQW5XM40mRVFET/zMz+Dhw8fQhAEJJNJfOlLX0I0at0YQCdBMjtCJElCNptFKpVCNBrF9evX+0qsXbnebDSXHbBt6xmCrQyQWFlZaVvN2olTFnkpq7MjqcD2Q1GdHVZi+1Vn9UisGnolFtDeWpCrxRAJaH/Pm1GV7QWT2rOz/aunRvpkC/yz1ya13/rd9JJaNZF1SlVWS3uBGegZrsIkt13qF7ES+6Ep++JUnLwAzEy0juYalHJWLBbxe7/3e0gmkxBFEcFgEJ/73Ofw/PPP4/nnn8fZs2cNn/dXV1fx8ssvAwB+7ud+Dl/5ylfwi7/4i4Yey22QzFoM65k9ODhAKpVCPB7HzZs3EY/H+/6cXSlcgL1tBnpmzZbLZSSTSZTLZU0BEk4RWYYZEmtWdbZ0YhFNnznvtU6hHVZic0Kr8hH266uIaxVZxk4hilOTg6uVZrYX9KJaA57uhLFyyvjipUHTCxip/fYqrZ5qLGPUVdl+WNGyMAxPy1fwtMNn//MV8yZp2I3X2wwYw8yZ7Uw5+7u/+zsAwN///d/je9/7Hs6dO4dvfvOb+MIXvoCtrS0sLi7iK1/5iq5t+Hw+WWQbjQY2Nzdx5coVQ/vrRkhmLSaXy+Gdd97B5OQkXnjhBc3DkdmsWZLZblgzfqlUwvLyMubm5kYqscO2GkTvPQAADZNOrad0csWyxx5WYoFnIgu0VvxrFVq9Intcbn0hGCS0oxBZJU93WgtrOqXWaHtBL1iVdmWhd9+uW6qyZmFk5LXWSQ7/+sNn5wFRAn7yqnvldpxk1uznWS6XcfnyZfzCL/xC2+2VivGFif/8z/+MP/mTP8FP//RP4969e8Puomtw1ldYDxIOh3H79m3cuHFDV8qHnULp1G1Xq1W89957ePPNNzE/P4+HDx/i5MmTAy/JRH79j6zYVV1E7z2Q/zA4k9LOuKY+sS6dXJH/KPGL5rzmR4EFHPtPDvUYOWGiTWQZg0ZYAcZFlrFTiGKn0P0YoxLZqkoxlkktMPw82X68ldHfyjHKquyo2gtGhfgjYf7G+zF84313pkB1yuy7WyLe3TL/i4/dWDEzOJfLqc6QH6bP9ad+6qfwT//0T0in0/jCF74wzO65CqrMWkwsFhu4ql4NZQrYqHFaZbZarSKdTiOXy2FpaQnXrl1zzZBppbxayaB2A60VWL/YMNxucBRYaN8nSJCg/3VSk1gl/Sq0w4qsEpLYH3IAACAASURBVK1tB2aiJrIMJrRn5vR/NvtVZRl8pWVWTGhvXXxWLTQyimsQZounmY9nZVW2H994P+a6Kq1yAZgXJdZKCoUCbty4Ycpjvffee0in03jppZcAAIuLi0ilUqY8thsgmXUoThPKUcGmGQBArVZDOp3G0dERlpaWcPXqVcdI7KBWA60SyzWbkCy6RGe0hUCv0HZKrBK9QjtIZHuhV2KB/iLLYEI7qj7ZQdQECant1jaWTnd/RoepynbyVibWJrR6MTu2dlTtBaNC7CHMbhNaSZLw/i4HKCaO3Djjrgq5XZg5miscDuMv/uIv8MYbb6Ber+Px48f48z//c1Me2w2QzFqMUfmyU2Z9Pp+moAcr8Pv9qFar+OEPf4jDw0NcvHgRV65cGVpiI7/+R6j+X/+7SXvZm1FVYtXgTy5BGlHnUD+BNYJeiVVWZ60SWcZ/7Mbx3PTgqySjEFklqW1/m9D2Elk9VdlO3srEcHeppPpvXm0vsKsqq8RNQhs7fdfuXbAcURQtKaSYKbPLy8u6F415CZJZh2Jnm4FdCIKAg4MDFAoFXL58GZcuXXLN/MJhJNaM6mzpOXNXrfaqzhqR2EHVWaPV2FozaCgdS4/IFsut999uLthXaM1a8NWLTpFlsCrtmXn1fz8u+uAfYvOVqoRvvdc+eeWD142FOzCc3F5gBCMi26sq++wxga8/brV7/NdrzpTaXi0FXqzKWjVZKJ/Pq/bMEvohmXUogUAAtZp9meKjpF6vI5PJYH9/H9PT05iamsKZM2dM347Z1VlfMIjwLXtnxHZKLAfRtOosE1ozqrBqQmtUYhnHlVYPaTSovSXGiMgyBgmtGkYXfCnpJbJKNvfaf7dnF1o/o0Vke1Vle/Gt9+Lw/WhzqyrVw1FXZc3EpgtSfWFSCzhHbMetN3aYsVz9KBQKJLMmQTJrMUYvTTihMmt1aEOj0cDa2hp2d3dx/vx5rK6u4ujoCIeHh5Zt00xC9x4BdXO+cOitzvarxJoltNnQ6aEfQ4lSaIcRWSaxjErdr0lohxFZhprQGglGYJghsmoCtrnHYTIx3Ge3Uh287Vd+tAJfTWrVoKqstqpsL5RiC4xebgdJrBersoA1Y7mAVuDPoJnzhDZIZkcAC07Qg509s8rt60ni0kqj0cD6+jp2dnZw7tw5rK6uyu0Edi4+00ro3iP571IwDM4kodWC2e0EapgtsZ2YKbKMQUJrhsgylEJrdZ/sIHodVuIxbZKltyoLQK7KKnlFMVbq7iXzPg/jVpXVuw9MbtVqDmb33I5bNVaJFZVZSZIsGfc1rpDMOhS7K7NWyGyz2cT6+jq2trZw9uxZPHr0qOvbrnKagRUM22qgFFmzGVSd1SOyRqqzvSTW6IitTg5rkwDUZWgQvSRWSS+hNVNkGbu5IBLR3id3KxZ8ddJPZIfpkwW0VWXVaIrA934YxoMr3U9QbxXVi4u+BlVljdDr4pna3FojgvvOprZUOK9WZQHremYB41dviXZIZkeAmyuzZtBsNrGxsYHNzU2cOXMGq6urPS/ZOLUy209ira7OOqEaO4zQMolliJI+odUisj1/1gKRBYAiL6HIt57Eqbn2z7aVC74Yw1ZkAfOqsoymwne+98PWa6YmtWZgd3uBEYZpLzCLXsEMapL7zqbVe+MerKjMiqJIVVkTIZl1KE6Q2WGlstlsYnNzExsbGzh9+jQePXo08IDg9/ttfd5qWFmN7URZnR1WYrVUZ/W0FOgR2k6B7USL0BqRWGV11kqRVbKT5WShHcWCr0Eia0dVttmjcMek9sVL+q4yOb29wOxRXEZF1qyiXqfkzif0VXC9XJUFrOmZLRQKmJgYbhGs1fzlX/4lvva1r+Hs2bMAgKOjI/z1X/81vvOd7+Dhw4c27107JLMjwMhlBDtnvQLDSaUoirLEPvfcc5okVrldqyuzeloNtIqsmdVZJ1RijTJIYpX0EtphKrEAsH0cRjSsvb9vGJFl7GRbT2RqwLnJapHVitlV2UF8553u3/EHnm9/jb73+Nkx4u7V3scAL1ZljWDF1Wm9EjsuNBqNoSJm1cjlcqbNmLWKK1eu4AMf+AAuX74MAPjZn/1ZvPzyy44TWYBkluiBkcqwKIrY2trC+vo6FhYW8ODBA909t05pMxhlNZZRPHPd9MfsrM4OK7G9qrN6JFZJp9AOK7LHpdYhrVLzaRJaM0SWUa1JqNYkLMypP+awC760iKyTqrKMalX986yU105ef79VBeuUWrNF1q1VWbNFtp/EDuqXDfJPAVw2d4cchhU9s4VCAVNTU6Y+ptmsrq7Kf//85z+PfD6P3/7t37Zxj3pDMutwrB6P1Qs9MiuKIra3t7G2tob5+XlDEssY1XPtV501KrJGq7NWSKwSK0dsGZVYJaIE5KvmSKySyo8u+feSWrNFlrGXbW2vl9T2ol9V1qyKLDD6quww9JJauzB70ZcTJigMU419LnKMXNWaOG4nYUXPbD6fd7zMMl599VV8/vOfx/e//31LRpSZAcnsCDAqaD6fD6Io2vLmCQQCA6cpSJKEnZ0dZDIZzM3N4f79+wiFtGXYO5FRV2OtllgAOAidNf0xszXzDsBH5Yj8d7/P2JldTWSVqFVprRJZJUqpNWOebCedIuumqmwgoG9nX3/fj1qtCUDEg+fNqc46QSSNYNb3fTNaCprNpmPlxkys6Jk1M8rWSnK5HD75yU/ii1/8oiVhRmZBMutgWHXULpmtVCqq/yZJEnZ3d5FOp3HixAncu3fP1RILjFZk3SqxgHUiCwBNkdMltIMkVgkTWj0SC/QX2V4S28n6VgPzc7331UifrJGKLGBuVXZUIgvgRyLb4nvvtG/YLLkdhBOqsmaIrB6J7ddicOOMDzs74yGzVrQZuEVmf/mXfxkf+9jH8NJLLwFoxc5//etfx0c/+lGb96wdktkRMGwKWDg83CVYI6i1GUiShL29PaRSKczMzODu3buW7dso2isiv/5HEF/5iqmP2a/VgCS2RafEKtEitHokVsneEYdY7013YYbI1motGdjPtj5LnVJrlsgOG1vbqyprV3uBHjrlltFPcu2uytolspdn9pCrD7+Cnk0vGKfKrNkym8vlsLAwfFS4lXzxi1/EP/7jP+JXfuVX8JnPfAZAK34+GAySzBLasXM8l3I0lyRJ2N/fRyqVwtTUFF588UVEIjqsQCd2tldYAUlsi34Sq6Sf0BoV2cKPxLRclRCLDLYCM0VWiVJqRymyZmNXVVYrogR89+3WTj56oX2bbg5IMMrlmT3THks5hsvKMAEnYYW0FwoFeUqAU/n0pz+NT3/603bvhia8/y50MVr6Vq3C7/ejXq9jf38fyWQSk5OTuH37tunjSdRgIj0KmfWtfsyy6uwoJBZwvshqlVglnUI7rMQqGSS0w4qsmsR2sp9tQKiLOHlCfaGkma0FgLlV2UEi6zR6Sa2VOKm9wKjIakn98lLRoR9WXCksFAquaDNwCySzI2CYNgM7KrOSJCGfzyObzSIQCIxMYhlsxq1b+3Dzz12FX7T+S4gXJVbJQT6AwBDnSTWRZfQS2lGIrFB/dp+Dw2fvEya2arKzsVnG1cvxrtvtqMoOwglVWTWY1D7U2WNr5iiuUYqsmsQO22LQGY4wLm0GVuCWnlm3QDLrYEZdmZUkCYeHh0gmk4hEIojFYrh58+bIts8Y9axZM6uz+eeuAgCavqBlQut1iVXSaEK30PaTWCWdQjtqke3k4LCOutD9vm80Wj/z/n/wXf9242q34HYyTlXZQZf260IT33q997Hlg3eNjRTUsw96MCKyZrYUKFFL+RoHmbUqvCifz2NmZsaSxx5HSGZHwDCV2V4TBcxGKbE3b95ELBbDK6+8MpJtd2JGlO6oYRKrxGyhtUpiAXNE9pCPmLJI5ajYfnLUI7RaRZbBhNZukQWgKrJ9H09o4o23CwCAOy/on/drZBTXIOyuyvZDy+/3W6+3f15/7EXzrg6NYtFZP5HVU5XtbDHoFVc7DjJrVSsFVWbNhWR2RHAcp/sb3igWgB0fH+Pp06cIBoO4fv06EomEpdvTwjBRuoZ5+N+BV/9vQz+qJrJm4vRKLNASWaB1wh5GaDtFljFIaPVKrPxzRRGFYuvv8Vj3CdtukWVV2a7H67j/G28XVIV2lKO4emFEZI2gtyL6P/9Loe3/i/UY/p9vtp8Sv/0Doe3/B8ltr32wur3Aqmos49///d+RSCTkP+FwGBzHodlswudzYK+LiVg1HrNYLGJycvjQGaIFyayDYaO5rEApsVevXsXExPDjWszCjkhbjuNgRIcGieww1VmnV2KBZxKrxIjQ9pJYJWpCa1RigZbIKuHLrf9nUmuGyA6SWEC/yPail9Cqobcqq0Vke1VljWB1VbZTZAFgIljGL/2k+pfov/zGLIBuuQXMrd4ynCSy104BlelFlEol5PN5bG1toVarIRAIoFqtIpvNYnp6GvF43JNVWqsmNkiS5Mnfl12QzI4Ip1Rm8/k8nj59Cp/P5ziJZdjRZsBxHF6RnsMjblfT/a2sxrpVYpVoFVotEqtEKbTDVGP7wZdF+P2Dd94uke2syipRth2MMrbWzPYCI2ityqpJLAAEuP7H2V/6ySPV2/P1BL76b62/T011S+3iWfXnH/A/2+GAweQ7PRJrtMWAtRfE43HE4/G2uaj1eh1vvPEGJEnC1tYWeJ6HKIqIxWKIx+OYmJhAPB5HJBKxJZLdLKyYMWtVH+44QzLrYMyU2UKhgCdPngAAVlZWNGVCcxwHURRHfhnJljYDHegVWa3VWTdILDBYZLWiV2Tln8tLMHJuGSSxQLeUxePdGzKjrQDQ3yML9BdZRoUX8J1Xsrh1+4T6v1tQlTUTq6qyaiI7SGIHMRUs4Zd+svv2N3dPt2/H3/t33hBbotfme4q7q8nuzdl1AIAgWReo06tPlhEMBsFxHM6fPy/LqiRJKJfL4HkehUIB29vbqFar8Pv9bW0KiUTCNVVJq2SW4zhXS77TIJl1MGa0GRSLRTx9+hSiKGJ5eVlXwzmT6VGPyPL7/ajVBoTZ28Aw1dhBQuumvlit9KrOGpVYACiUWif2RgO6hNaIyAIAz7dkh0ntKERWb3uBkgr/7DL4W28e9hRaNdSqssO0F9g9iovx8HYYl2YP2m4bVmIHcfu5bdXb//3glPx3rR7DZBcAbs+tyX+3UmT1oBQyjuPkKu78/Lx8e71eB8/zKJVK2NnZAc/zaDabiEajbYLrxCquFT2zpVLJEetTvATJ7Igw8gFlSVhGKBaLSCaTqNfrWFlZMTQCxC6ZDQQCKJe154ebSa8xXVa1FbhBYgHj1dhOoTUqskxilWgRWqMS2wnPN2TRisfVxzdpkVjAuMhqqcp20im0VkwwsJNBIvs/Pnjc9v9WS+wgbp7c6brt3ewplXt2w0RWr8QaaTEYVJXVSzAYxPT0dFsxRZIkVCoVlEolFItF7OzsqFZx4/G4rSljVvTM5nI5TVdHCe2QzDoYIwJcKpWQTCZRq9WwsrKC2dlZw9u3K07XzjaDRqMB5WHcTIlVVme9LrFKhqnEAuoiy2Bvk85zjRaJBbQvWlJWDHm+9RoqpdYJIqusyip5681DAOhbpXVrVbYfSpG1W2L7cWOuW3Dz9QQ28y0JHXU11myR7QXHcYjFYojFYm1V3EajIVdxd3d3USqV0Gw2EYlE2iQ3Go2OpIprRZtBPp8nmTUZktkRYfWHjud5JJNJVCoVrKys4MQJ7ZcXe2GnzI56AZgkSWg0Gvjud7+L5557ASf86mIwLFZIrNkCC5jXF3tcGr6lQAvKKq1Z1Vigv2Axqa1WGpiYGiwZRnpktdJLZJW89eYhLl81/uXWafSqyrpFYvsxFSxhaq6EIFqvq1GJ1Zv4NSqR7UcgEMDU1FSb7EmShGq1ilKphFKphL29PVQqFfh8vq5eXLPFs9FoIBIxLwgGaFVmacasuZDMOpxBi7DK5TKSySTK5TKWl5dx4sQJ08TZLpkd5TQDSZKwv7+PZDIJSZJw69YtecLDcfo907ZzFFgYfCcValIIHCSEuO5+2yOhdbD3ceamDpmR4DWMxAL6RJaN1AK09SGaIbLyY1Van49ivtZXaAeJ7DBVWS0iCwD1WgPvvrXfdtuNW/NyVfadN5/9W11oPa9b99oXMilxYlWWiWzyeA6xUPdjnkscdN3mRJjEAkC2PovJQHf6m9m0Wgy0v3ajXJHPcRyi0Sii0ShOnjwp366s4u7t7SGZTHZVcePxOGKxmOHzohU9sxSYYD4ksw6nV99qpVJBMplEqVTC8vIy5ubmTK/+2pXENarK7OHhIZ48eYKJiQm8+OKLePz4sSUrbIcRWYYgtS5ph7i6LLFKhhXaToHlOGOD3u2SWEa/kWB65qDqEVlGMd9atNgptVaKrFbqNfUvpZ1yCzwTWQB467VtVaF14iiu//HBYySP5/r+3EbpZNdtThLcTollFBrPYovNFtvn5YtF+l47J6R/9avi8jyPYrGI/f19lMtl+Hw+xOPxtipuMDg4vtiKntlCoUBtBiZDMjsijIpmp8xWq1WkUink83ksLy/jxo0blrUw2NW7avV2c7kcnjx5glAohOeffx7xeFzernLB3czi9aGqs0YlFmgXWSWCFEQiWEapHjP82Er6VWH1CO2wEgtoF1k1iVXC9ln5sbCiGtsLZZV2GJHVgpaqbC+R1UovoTWLYauylxdDmIw120RWrSrbCzXBBUYruUqJBYCF+Tmwo8e7W+3vEa1i26/F4HkTup2cILNqKKu4c3PP3hPNZlOu4h4cHCCdTqPRaCAcDnf14iqvhFrVM2tkUTbRG5JZh8PGc1WrVaTTaeRyOSwtLeHatWuW9+EGAgFbRmRZVREuFovyrF21wAifz9e1XSNCO4zEAt0iK4FDZz6ZmtDqqc5qbSUYJLROkthOJEmfKJkhsoxivoYyL2B2zviXDjPaC/SKrLIqq0QptE6ryk7GrLmKM6oqrlJkF+a7K8v9+1gn8O6WOLBaa4a8duK2KFu/34/Jycm2CFlJklCr1eRe3IODA1QqFXnEWCKRQKVSMb2lolAoYHFx0dTHHHdIZkeEUfHkOA6pVAqVSgVLS0u4evXqyObwBQIB8Lz1vVqdsD5hs+B5Hk+fPoUgCLh06VLPXiUz2hvMFtleCM0QQr6WeAjis4/xIKE10g/L3m7K47kZEpsrSpoTp/SKbLncLmX9Er20Cq9WkS0rJPMoW+4ptFb3yZolsgy9Fdq3vr+BRr2Bux/ofdIetip770b3+1BPVVYvZlZxgxDkVoK54JGqyGqhJbvPvphv7BUBWCOwSkRRdGRlVg8cxyESiSASiXRVccvlMorFImq1Gn74wx/KV0iVVdxYLGZI6Kln1nxIZh2KIAhIp9PY39/Hc889h9u3b498mLRdC8DMep7VahXJZBLFYhGXLl0aOOGhl8xqqc4OK7FAf5HtrM6G/AKEZuv+IV9joNCasagLMEdigZbIAq397Ce0eiUW6BZZAGg2JVWhtVJkGWpCO4o+WSt467VtXLnZ/V4PBHx46/sbbbc16q3f2evfSfcVWj2YudDRTPRUcZUSCzAZNSayapxbGE1EuVPbDMzA7/djYmICExMT2NzcxJ07dwC0zsusint4eCjPQ+/sxR00m51k1nxIZh2GIAjIZDI4ODjAxYsXsbi4iEAgYEsqil0yOyyCICCVSuHo6AjLy8u4fv26pt9fv8psL6E1Q2KBVh9c2G887a2zSntUjmA2VnWsxCphgqKUWrMkVkmz2doQk9pRiCzjKNs66c3OxRzZJzuoKssQKgLe6ZBWAPB1tBgwkWWoCa3eqmynyI66KquXTsGdDFe67uOEUVhG8bLMdsLOH+FwGOFwuK0wIoqi3It7eHiI/5+9Nw+S5CzPfZ9au7qWXqen932fGTT7SIMQBObYOA6Xq2vDsYmjG7YP9/rGRVzZgCSHCctgbFBACGMBxmBCmMNybewjbF8bjgFjIxmEQELrSOruql6qurt632qvysrl/tF82V9WZe25VFbnL2JCo57uqurKrMzne7/3fZ5QKASGYeB0OuHz+USh6/F4xCqu2TOrPKaY1YhSYiqbzSIYDGJnZwfDw8O4efMmrFYrwuFwzZG21WI0McuyrFjNHh0dxfT0dEWLgNwBsFIoKWQBIMM5igraYtVZ8WtUlVYNi61qXQ7kRGwuvACkUsqL2FxisWMx6HQWvxGXK2KB4kKW5mAviZa2wselHtsLCExK/rlzhWwhaEGrdEACUF9CthRGFrGE0yRmi2G1WsUqLg3DMIjFYkgkElhbW8O//Mu/4Bvf+AZGR0dxcHCAF154AV6vF93d3VUXq5aWlvDQQw/hypUrWF9fR2dnJz70oQ8p8WsZDlPMaojFYslrJGdZFsFgENvb2xgaGhJFLMHhcOgW7aqXNRdBEISyPuQcx2F1dRUbGxsYHBzMew/LRW4AjIZUZ5USsYB0MlkJUtyx1Uy7O4PDZPVpQcUqsZUI2nJELKFSIVupiE0mpQsFhuEKClolqrG5pBIZyX+7+6XWPHoI2XKpRMjmVmVpqm05KKcqW8+QqmwjiFjCaRCz5d6D5HA6nejs7BSruOfOncN73/te3Lp1Cx/4wAfwk5/8BF/60pewtbWFM2fO4OLFi/jt3/5tzMyUnzp5cHCAd73rXbj77rvF53jb296Gq1evVvWajYwpZnWCZVmEQiFsbW0VFWB6Vkf1fG6y5V/MEoXneayvr2NtbQ19fX244447arq42my2klXw9tFzOFjbr/o5ACD+cwErJ91qrc4227I1Cdpy2wlKCdpqROyN2eNz7Zm50pelWoUsgQhIWtSqKWRptsMRAPmitlqqEbLlVGVrrcjm8vS/LQAArrxhoqqfl6Neq7J0a0EjCVkARcN8GgWlBbvL5cL169cBAJ/85CdFoby7u4uXX35ZtIksF/JYBJ7nK36MRsEUsxpisViQzWaxtraGcDiMwcHBkgKMWHPpgdVqVdRVoBKIkJYTs4IgYHNzEysrKzh79ixuv/12RXwAbTYb0ul0ye8bH+zEUhWCNk5VYYu9q6UEbSW0u49FVClRW01PrJygraUSuxd34oyXKSpqlRKxuZAqrVZClmY7HAGTZtA9WDhqttyUL70pVpXN5fkfLeZ9TU7gGrEqK9cf22ioESZQb6jhMStn89XV1YW3vOUtNT3uP/zDP+Ctb31rRZXdRqKxz8Q6Y21tDSsrKxgYGMDNmzfLWvEZrW9VKeSGsUj07PLyMtrb23H9+vWSU6O1PmchKhG08ZxWgnKWB8UEbSXVWUKhKm2tg11E0KrRTkBELQA88Vxlr6tcESt+f5wBaeZxNRdPBVJSyAIAkz5+vO21AwDIE7VqtRcoXZUtR8gWejwAsFgteOHHS3lf97Yef37Gz/XI/ly9VWUbbdCrEBzHoamp+lYmI6BGlC0Rs0oOdf/gBz/AD37wAzz66KOKPabRMMWshrS2tuKOO+6oaKWnZ2VWT3KFJR09e/nyZbhcykzpF3vOUhQTtLkCFgCy/PFF0WbV/uabytrhcnBIZ08uzEoGHtisAFdCoxYTsWODhW/2nGDBXVekX/vh84XFczVCliadyhYUtOUK2XJELHAiZGloUWsUIQsAv/ifC7cNsNzJ8fruP87l/bulgD8bEbIAsPTaFn79v/QXfA69afu5iNVnL0t7TkPPrBrV52QyqWgrwLe//W388Ic/xKc//Wlsbm4iFArh5s2bij2+UTDFrIa0trZWPFClhJF/rdTSBF8tZPisUPSsGlTqZgDkC9piIpbAlSlqlazONjtYUdACwOZhbRVtudSuQoK2GocCyeNaBHCC9Py764oFws+/9qMXjh+/VhFLk04dPxYRtWpVY4ux5t8CAJzpL9x+oPXAVyHe/IsjRf/dTnn8vu0d58S/0yIXAIKh4/q4/6VViZAtRD1UZdtKtBQ0YlUWMF4CWDWo0WZwdHSE1lZl+uSfe+45/Pqv/zquXbuGN7/5zUgkEnjve99rilmT+kMPf1macgax1IDjOMzPz6OpqUk2elYNSrkZFGJ88MRz8KUVac9trpClKUfUKtk/S9PbzlQlaEtFz+YK2kqFLOmbLQeLRYAgWPCGy1Z876nKYpeLCVmadCoLvgKnfqWELC0m98LHldpcUVutkC3XiksOuapsKSFbCIsFcNil17fJcQ+yrICR4ZO+PyJw77qu/G5MLciJ2NyzfbKLBaBcK1Q9cRoqs2qI2Wg0qpiYvXr1KuLxuCKPZXRMMashegvTaiAVUq3ELImePTo6wsDAAMbHxzV5XkCZKvjF0cpuuC+//DLGxsYQ2C38/hYStNVWZwm97ceCqRxRW0rE0tisQDxRvogt1mJQLr9053HvXilRW66IJaSTJ9/vdBXvpVVDyNLshQ+KVmnLQcn2glpEbDEKCdxcqahXVbZUJZamkSuXjRBnWwo1emYjkYhiYtbkhMb9pDUYchOQWmCz2TQZQEun03j11Vdx69YtDAwMYGRkRPPhAj1aOkg1+PKoC5eLCOEMJy+kBNS2QEoydrR6CgvPaFyoSMgSvB59Li1E1MpRiZBNJxmJkAUAJi1fIU8lMqoLWcJe+AB74QPd/WTVErKFGDxbH52olQjZ1ObzDS1mT0NlVo1CztHRkRllqwJmZVZDqq3M6rXVD6jvplAoejaVSmkuLPUSs3SfLhG0L6yUtgiTo9LqrNvJioI2kji+8VYjXmnKrcqe2GyVrgzL9c0W4pfubJJUaGupxuZCBC2p0tYy6JX3PWX2qTLpDHbXdyVf6xroKvDdJ5Sqypb7/FoLWTm0rsqWI2Jzz3o9Zg205DSIWZZl4Xa7FX3MSCRiilkVMMWsASCOBo0kZktFz9psNjCMtt6aevjqFnpOOVFbbrtBtZAKbTRe3Q24chELXJjOF7LV9M3SZDkr3nxHMwDg4aPrVgAAIABJREFU29+PlPU4QHERmwuTzoIrZd8gfm/xx61k2IpJy4vnndUd8e9nh87m/btSfbJ6CNmeDqlw1VLIVlKJpTnfb8WzG8ZsLSuX0yJmlb7vmmJWHUwxqyHVXtgaKQWs3OhZPaJ0rVar5u0cpRwUJrtYST9tOQNh1VZnCYPdAta2yz9XK+mPrTT0oBocNh5Z7vicett/OulNKyRsKxGxAJBKSKvmTpd8ZVnJauzx48kLWSFnQI0IWzlRW+nr0FPIunWc9/I4GDh0sNAzEo1eeQbU65kdHBxU9DFNTDFrCPT0mlVKzFYaPatVr67eFHJQSKfTCAQCSKVSmJqaQltbm1illRO0SlVnCZ0/LxzsHxX+Hq1FbCWtBnL88i+cCNvv/PuxsK1VyAInopUWtUq3FRQiV8jSEFHb3lN8aKyc16GXkG1xa1uV9Tiq2w2iPwmNasUlR6OLWTXa+5R0MzA5wRSzBsDIldlqo2frwV9XC3LbDLLZrKSHuKurS7xhVNJPW2t1ltDZli9olRKxci0GhEpaDaqBFrY0//itXdmvy4nYXJg0A6fLWRdC9uTn09gObgAAukf6KnodVrsVU6/rQ39PddZSRqvIVitkczkN2++nBbPNwDiYYlZDjNpmUE3vaq3Rs6elMkvaDOj2i5GREUxNTRU8Xy6PuvDCClStzrqbBCQzx89PV2mr6YtVG7m+WbrVgFBOStn/9r9IB6n+5m/XKnot8cNjz0dnc4HWAwXaCoDyhSxNMVGbi9Vu1aU/lhayWlVl5URstS0GtpgfL2zGwfM80uk0gsEgfD4fvF5vw0e/NiJqtBlEo1FTzKqAKWY1xmKxVNyXqWebQTWiUonoWT16Zgla9oJZLBbs7+8jFAqV1X5BKCRoaZSqzhI624AW7/Fr29iWPzZaili1cdgF/MY9AwCAr/6/60W/N1ek0v9PhK2eQpaGiNr27jOy/261W+Frqy5pTykhqwWFKrGVCll6fTQzcxz2wPM8nnnmGbhcLhweHmJtbQ0Mw8DpdMLr9cLr9cLn86G5udmQ9l16WUVqjSAIih+fSCSC9vZ2RR/TxBSzhsButyOTqSzhSMnnLlfMKhk9q1ebAVlsqC1mBUHA7u4ulpeX0dzcjBs3bsDhKG7Kn4ucoFWrOptLX/eJ4N7Y5vJE7OjwcRXK+vMfXwpKz99iLQbFqLVvthKyrAUO+/F7+Rv3DMgK2nIEaqXRsGoKWQLLsNhd25J8rWuwBwBw6cbxcMphRPr5a28tvsgq9ZE5255fFnfZT55jL3Zy/qtdlVWqpYCG7pW1WCyw2Wzo6emRfE8mk0E8Hkc8Hsfe3h6SySSsVis8Ho9YwfV6vbo411QCz/MN3y+rFmabgTrU9yemATFaZbYcMRuLxRAIBABAsehZvcQseV41qyWHh4cIBAJwu90YHR1FNputWMgSSlVola7OOuwCsqz0JtbXbROjeQsxPpK7xVr6M1CrRZcc5bQaFCJX0FbT9+p0Fd9q1krIyrG7toW3/vrtBX8uV9zSWCzFxa7XLf/a0+zJz3ibTw4ML1gkQpflLLDbal+klRKxSjkY8Dwvew1pampCU1MTOjtPIrA5jkMikUAsFsP29jaWlpbAcRyam5vFCi5pU6gXAXka0r/UgmXZilruTMrDFLMGQO+e2ULPTaJnGYbB5OSkoqtNPWyygBMxW624LEY8HkcgEIAgCDh37hy8Xi92d3eRLkOAFOPyqAuvrWpfna135Ppma4W0HTz22HLJ75UTpkw6U1DQlmu9Jf+z5Z1DhYQsgKJCthhEXxWq5HrdAtxNlZ+PGdaa8/9Ak126EilX4KpRiaXJdTAoJGblsNlsaGlpQUtLi/g1QRCQSqUQj8cRiUQQDoeRyWRgt9slFVyPx6NLm8JpGHKr5BiWy2lpz9ADU8wagHqrzKbTaSwtLSEWi2FyclJSZTA6alSE0+k0FhcXkUgkMDU1JemXUiqo4dyQD6+txmT/TYvqbKGKJy+ctBo0CnYrj//7/xoBAHzhi8G8fy9WXaX/nRa1agvZYiJ29vZZDI20FPz3YhQrFB5GOAz2WqsSsoXIFbj5uVvH0CK3XCFbTVWWh7wVV61CyGKxwO12w+124+zZE7/gbDaLWCyGeDyOtbU1JBIJAIDH45FUcdVYjNOcBjGr5u9YLxX2RsIUsxpTzUmsZ2WWFneFomcbCSVTwLLZLFZWVrC3t4fx8XGcP38+7/1S8vloQVvv1dlUxoLmMkSOXKtBrX2zlbQa0H2zBJa3wm49fgAiagGIbQ6f/ex8WY9NOx44m53g2ePHtNqtiB/GSgrZ4VlljNfVELIAahKy5Z67+eKWwMPt1G8YUY2qHnBc2Ojo6EBHx4l3MM/zSCQSiMfj2N3dxcrKCliWhcvlEiu4Xq8Xzc3Nil2vT4OYVcOWK51OVzUQbVIaU8waAD3FLBFbgUCgYPRsI6FEZZbneayuriIcDmN4eBh33HFHwRtbqQSwSilUoT0N1dlyLbrU5r77ZiT/nytuve35PeVEyJK/u30nw5MWmTdP4AXsbRxKvnamr/IJaTWFbLXUughrd1feUlBtr2yhgAS1xKwcVqsVPp8PPp8Pvb29AI63s9PptDhstr29jVQqBZvNJqngejyeqkSpKWar4+joyAxMUAlTzGpMNSJQr/5R4n2aSCTQ1NRUMHpWLSwWi6Y3BaA2MSsIAjY2NhAMBtHb21uWzVahBLBaODd0LJZeW401RHXWKBQaQssVtwDw5a+Hy3vMClYBRNyyWRY9w10lvlt9IVtNVbaW87UaEQtUL2SLLUG1vm7lYrFY0NzcjObmZnR1nZwLLMsiHo8jFoshHA4jkUhAEAS43W6JZVipASW9fz8tMAMTjIUpZk3yyI2e9Xg8GBoa0vx1EK/ZehezgiBgb28Pi4uLFQdEKNlmkMu5IR/mVqPi/zdSdVYviy4C3WpQDf/tf++X/fqX/nvpkIZi7Qds9ngHZyuUn2RGC9x6FLK1UEjIliNUZ/utmAtXfiyLxdbWq9iz2+1oa2uTCCqe55FMJhGPx3F4eIjV1VVks1k4nU7JsJnb7RaLMaelMqv07xiJRMzKrEqYYtZAqO1/Wih6dnNzU9MgAQIJbFB7mCH3OSsRl8Rb1+Vy4dKlS2hublb1+SpldqhFImhrQS9ng1qjbatNA6uGci3CCvF//NYgPM783/Wzj+0AKE/IFoII3BtvGq/qtaktZKupylZbjSXcNnj8nLNFhGk1QrdexawcVqtVFKwEQRDAMIw4bLa7uyt64nq9XvA8L7a/1bsnbrVwHKdKm4FZmVWHxjwL65hqBSGp4KmxGibRs0tLS+jo6MirLJKLlpaiEtDHa7bcbf9EIgG/3w+e52vy1lWjzSAXWtDqWZ2VQ+lWg1rFZCXUWp0tRIJx5gna+/7P44l2t/346x//i8O8nyuHRhGytYpY4ETIlqKY0C2EHot/JbFYLKIn7pkzJ0lxHMeJTgrxeBwvvfSS6IlLV3HryRO3WtQQ6tFo1KzMqoQpZg0CsedSWszS0bNXrlyRnbQ8TWK21HNmMhksLi4iHo9jcnJSMlVcDWq2GdDMDh1vK9dapa2lOmtkmy65VgM9+f17j4e9iKgtVZXt7G3H+FR156qaw15AfQvZajFSZbYSbDYbWltbcXR0hKamJvT09IieuLFYTOKJ63A4JH24brfbUO8Jy7Jwu92KPqbZM6seppjVmGpXq0o7GlQSPauXm4Iez2uz2WSjg1mWxcrKCnZ3dzE2NqaYLZlWYpbg4vYBW2dDVGe1tOiqBCWqw3LVWQBIsk6xOguciNqPfjq/R5aglZBVe+CrUhGrVJpXNTSqmCXQPbO0J253d7f4PQzDiG4KoVAIyWQSACR2YVp44laLWj2zU1NTij6myTGmmDUISgm7aqJnySCW1tRDZZa22RoaGipqs1UNWm/FWSwWtNhi6B/qx0sr1SWP6VGdrTXaVi2LLrVaDSrlD993Ju9rf/LoXtVtBUBpIUuj5sDX+c5j54eNVGmHhnJQuyoLNL6YLaflzel05nnikuhe0oe7vLwMjuNET1zSquByuXRvU1CjZ9aszKqHKWY1ptoPaK0pYLVEz5JBLK3RQ0QTMUsPw/X09IjDcEaHrgRfHHWJglbv6myjoWbvbm51thDHAjci+dp3XyivX6+cy5SafbJEwCqNFkIWaHwxW62bQaHoXuKJG4vFsLm5iXQ6DbvdntemoKWDgmnNZSyMf3c+JVRbmVUielavNgM9RLTNZkMikcBPfvITtLW1VWSzZQRyB84ujh73SFdapVXa2cAInrOF+ma1HAQj5ApaQbDAYin9/r31ckT8fprvvXgiLvQUskqJWLkWA62ELGCK2Uoo5ImbzWbFNgU6utftdkuGzdS6Ppti1liYYlYHLBZLxSEIdru9osqsktGzeorZWqrRlRKJRDA/P49sNotr164p3vxfD1itVtn3lFRpla7OyqFkq0ElfbNaWnQB6jsrVCto5filS8eDgfTPf+9F+Squ0gNfalVhabQUsgBE66pGRQufWYfDgfb2drS3nyTbEU/cWCyG/f19hEIhZLNZNDU1Saq4SkT3qtEzG41GJb+PiXI07qetwXA4HEilUiW/jwwqKRk9W6mQVgqbzYZ0urq+zkpIJpPw+/1gWRajo6PY3t5uSCELFB84I1XanyyW19pRTnVWL5suLS26AH2qs3KUK2jLeX9+6VIk72tz2yc34lr6ZCsVsEr1y2pFo1dm1bKJLEUhT9xMJiNWcXd2diTRvfSfSl6zGr+jWZlVD1PM6kC1ldli1VESPUsGlZSMnrXb7WUJaaVRuyKcyWSwtLSEaDQqtmCkUilsbGyo9pyF0MqXspxz744Jmyho6606qzf1ZtEl1z9bi6At9bOz3fn+tqGj8m7OFzrXy/q+WsltMdC6Kgs0vpjVOpmxGBaLBS6XCy6XS+KJy7IsEomE2Icbj8fB87wY3UtaFZxOp+y1V41rMsMwsvaXJrVjilmDUGgALDd69ubNm4qvJvVsM1BjAIxlWQSDQezs7GBsbAyzs7PiRUsPBwUiMLUQs6WswARBwMbGBrjtIPr7+7HFDhZ9vHqozp7mVgNAe0Gby3DbkezXfbZ42Y+hFnoIWeD4uqz3NL6aGCHO1m63o7W1VRJSwPM8UqmUGN27trYGhmHgcDjyonuVptIClkllmGJWB6q5yOUKykLRs2qglzWX0s/L8zzW1tawvr6OwcFBWZstteNl5SACWotKRzExu7+/D7/fj/b2dty4cQMOhwMjAH6yWD/V2VqjbdVEz1YDvQVtLkoK2WpbDPQSssDx9bleKpdqYUSxbrVa4fF44PF4JJ64dJvC/v4+EokEkskk5ubmJCJXiXusEd83I2CKWYNAxCyJnl1eXkZ7e7sm0/Z6WXMpVSUVBAFbW1tYXl5Gd3d3UeGvRbys3HNqJaDlnisej2NhYQE2mw0XL16UVCUEQcD1UYDnGfxoUf48U7o6qxRa983W4+vQS9DGOK8ulVk9gxJoGr3NoNEg0b3E7YfjOLzwwgvo7+9HLBbD9vY2lpaWxOheug+3XE/cTCbTUM449YYpZg2Cw+FAMpnET3/6U/h8Ply+fFmz3hsjW3ORuN6WlhZcu3YNTU1NRb9fj1WzltVgWszS0bzT09OSwQRBEMDzvPi9FosFb5xi8R/+40uGUtVZOfSw6apEbBfrm6236ixw+gQtoG9VFjDFrNEh8e1ynrikTSEWi2FjYwOZTEb0xCVVXI/Hk3f8I5GIpOXBRFlMMasDlQomEj2byWRw5cqVotGzamDEntloNAq/3w+Hw4Hbbrutrt0JtKwGWywWcByHpaUlbG9v50XzyolY+nx949TxeUBELaHa6qxSrQa19s02Co0maKtpMdBbyAKmmDU6hWy56Ojes2fPil/PZrOIxWJ5nrgejwdPPfUUent70dXVpZiY3drawkMPPYSXXnoJzz77rCKPaXRMMVvH5EbP3rp1S3MhC+gzFFXt8yaTSQQCATAMg6mpKUOshLVqMxAEAbu7u9jd3UVra6ukZ5iIWEEQxGG0Youu4yotilZna0Gp6uxpbDVoNEFbLg4rVxdCFmhsMXsaBpkqjbJ1OBx50b08zyORSMBms+Fb3/oWXnnlFWxsbODtb387Ll26hEuXLuHixYsYGxur+Fz50Y9+hLvvvhsvvvhiRT/XyJhiVgdKVWZriZ5VA70a1it5XoZhsLS0hKOjI0xOTkosWuodLcTs3t4eAoEAfD4f2tvbMTIyAuDkxkQifC0WS9kX1uMqLYvvvHLc7pJbnS034taINl312mpQikYWtPUiZIHGFrNGcDKoFSXSv6xWK3w+H9797nfj3e9+N77//e/jhz/8Id73vvfhpZdewosvvoi//uu/hsViweOPP17RY7/zne/EE088UdPrazRMMVtHlIqetVgsDX2RrAaWZREKhbC1tYWxsTHMzMwoIr61ssoC1K18x2Ix+P1+cbjLarXi1VdfBSBtKSCV2Gp+51++kBYFrVHQ2qILqI/qLGAcQVtJi8HVYe3boIrRyNdpU8xWRyQSQXt7O4aGhjA0NIS3v/3tij7+accUszqQKxjKjZ4lvavmRKTUX3dgYEDRkAhSKdXqgq1GZTaTySAQCCCRSEiGuxiGAc/z4DiuYF9sNfzyheOktu+84qqqOitHsVaDWvtm1aYeqrONIGjLod6ELGCKWaOjRpStmf6lLqaY1ZFKo2f1FLN6VoXpKqkgCNje3sby8jK6urpU8dcllVIjilk6EGJ8fBznz5+XvHfAcRvLa6+9Jk7qer1exarQv3whjb9/rrnin1Oz1aBe+mYB7V9LMUH7P57MH4r8L29K5n2tXgVtPYpYQiOHJjSyUCdU2jNbDpFIBGNjY4o+pskJppjVAZ7nsbKyUnH0bKEUMC3QS0jTVdKDgwOx7/Pq1aslbbaqReuBNyWsuQRBQDgcRigUwsDAQMHhLovFgps3b4rWMmtra4jHj4WF1+tFS0sLfD4ffD5fxWKe+Pn2MkFsOn9B/Lpa1Vk1UMqiC1CvOlsptKB9/D+KLzT+x5Nu+HwOvP9/zYhfm1tP15WgnWw/gNfrBVDfgqpRBd9pqcwqbX0ZjUYVG0h+8skn8bWvfQ2bm5v46Ec/ivvvvx/NzZUXERoJU8zqgNVqhd1urzh6Vi+LLPq5tRazdrsdkUgEKysrsNlsuHDhguqODloHJ9T6fGS4q6OjQ0zuAgoPd1mtVrS1tUm2vDiOk3gnkhxz4p1IRG6hagWxjyMLDaczBQAVVWmVqM6eBouuagbBSolYQq6QBYDZgfyb+mtrx9+jlqAt1C971rqCcDguLsA8Ho/o7Vns/DRRjtMiZtWozCrVZvCmN70Jb3rTmxR5rEbB/OTrgMViwdDQUMUWJ/VQmdUSYk7t9/sxOzurmc2W1pG21bYZxGIxLCwswOFwyCZ3VTLcZbPZZHPME4kEotEotre3sbi4CI7j4Ha7RXHrcDgQDAbBcRzOnTuXt9D41asp/P1zzapUZ+s52rYY9dT2kEuukC3EuUHprsjcerqq5yu3QnvSUjAofo2cn7FYDLu7u1heXhYTmsjugtfrVW0H57RyWsSs2TNrLEwxayDqoTKrBWQg7vDwEG63GzMzM5IUFrXRo82AYcoXZel0GouLi0gmk5ienpYI0FKhB5VArGV8Pp/k8ROJBA4PDxEIBJBMJuF0OuHz+bCzsyNWcekK/q9ePa7S/u1PSwdXqNU7q5aA1KvVQAmbrlw+dE/1r1OuektTTOwWE7SXBjI/79fP37YvdH6mUinEYjEcHh5ibW0NDMOgqalJktDU3NzcsD2tanMaxKxaPbPt7e2KPqbJCaaY1QmLxVJVZTaTKa9yojRaiFmO4xAMBrG1tSUOxM3NzWlaJQW0F7PlthnkDnedPXu27OQupRAEAYeHh1hfX8fQ0BD6+voAHIdVEAERCoXAMIxYISNV3F+7cdzqUI6o1Qo9LLoAbauz//PHpYVHLUK2HGYHXOJOgtfrheAdkfw7LWhJi8GlgYx4XgMQPyO0F3KuwKUTmrq7uwEcn7MMwyAWiyEWi2F7exupVEoSQerz+eB2uxu2z1VJOI5r+PdJTWsuE3UwxayBsNvtYkyeHs+tlsDjeR7hcBirq6vo7++XDMTZbDbNq9F6iNligr3c4a5ykruqRRAE7O3tYWlpCWfOnMH169clF3uPxwOPx4Oenh7x+9PpNKLRKCKRCNbW1pDJZNDU1ISrncfi9ongqCqtBvVk0QXUzyBYIf7z9DN4+uks3G63KOx8Ph+ampoUOZey2SyWlpYQj8cxPT0tqaRKcWF9cw83xshxPqnuk3Oc/Jd8PmmBS/7ICdympiY0NTVJwlSy2azYJx4KhZBMJmGxWMQ+XFLFbfQqZKXwPN/wvclqiNl0On3qh7TUpLHPyAZDzzYDNUSlIAjY2dkRBRI9vEQ/r9ZRuvUkZnd3d7G4uJg33AVAvKlXmtxVKSRW2el04tKlS2VN+VosFjQ3N6O5uVlSIctkMojFYohGo5hu+jFSqRRW8BbJzxqt1UAvymk1KFWVPa7IXpNszx8dHUkWH3R1vZLteUEQsLGxgdXVVYyMjJS0HgSAgV755D56cUvIFbh0BVcQBFit1oICFzje6Wpvb5dUy8ggZDwex+bmpjgI6fF4JFXc3OtU7u/dyHAc1/B9yErbj5FzwmxtUQ9TzOpENSe13gNgSrY4HB4ewu/3w+v14sqVKwUFkpoV4UJoES9LIzdwRrZkiYCkV/RatRRkMhksLS0hmUxicnKy5gE8i8UCl8sFl8uFrq6TafWrzBGi0Si+Fxgq+vNq2XTV2mpQqm8WkK/O6imuc9sKCm3P04uPzc1NpFIpOBwOUdS1tLTIbs9HIhH4/X60tLTkVfGVolKBS/9cIYFbaBCStNHs7+8jGAyK1k20wCWVbC3TA/XgNPTMqkUjnxd6Y4pZA6H3AJgSLQ4kXtVqteL8+fM/94sszGlpMyDPl06nEQgEkEqlVB3uKgbHcQiFQtjZ2cHY2Bi6urpUvQg7nU6cOXMG//XMsWH/Xz/tVjVEoZGoZhCs3P7YQosPuv90ZWUFiURCHMZyu904PDwEy7KYnZ0t+flWmnIELvk7+cwJggCbzSae43KDZl6vV/K7kDYa8j5sbGwgk8nA4XDA4/GAZVkkEgm43e6GEzCmmK0cNdwRTKSYYlYnjFiZrUVUplIpLC4uIpVKYWpqqmyLEpvNpvnQW6XuArVitVrBsiwCgQB2d3cxMTEhEZBaDndtbW0hGAyir68PN27c0GXQ47/ePBa13/hJeYNiRuibLYSa1Vm5FgMlBr2cTic6OzvR2dkpfi2bzWJlZQXBYBAejwccx+GVV17JC+LQo9eykMAl/y1UxS3Vh0vaaM6ePSt+nWEYHB4eYn9/HysrK0gmk7DZbBInBa/Xa+gBqkYXs2pU1iORiGbWkqcVU8waCD36RwnVitlsNovl5WUcHBxgfHy84iqf3W5HMpkfsakmWr7PPM9jZ2cHe3t76Ojo0GW4C4BotdXS0vLz0APtI5NzedcdJ8edCNtaWw0qEY9atBooQbnVWbUcC46OjuD3+9He3o4777xTFKw8z4sDVltbWxKfYroPV49zrZAbQqk2hWICFzgW+m1tbfB4PLhw4QKA46oceR/C4bDhAx8aPc5WDbFuesyqjzE+PQ1INaJEz+2qSsUsx3FYXV3FxsYGRkZGMDU1VdXr16vNQO2eWeIOEAgE0NbWhtbWVgwNDUn+XYvhrmQyiUAgAEEQcP78edXT1aqFFrYA8P+9oOxUsFZpYCxvxRc+78f/894JVZ8ntyqrhpBlGAaBQACZTEb23LFarWhpaUFLSwv6+/sBnPgUk/7TlZUVZLNZSdBBS0uLYk4KlVKqTYHeISkkcDmOk7x2u92el7hn5MCHRq/MqmXLZVZm1cUUsyZlUe4gFm0j1dfXhzvuuKOmC58e1Wi142yj0SgWFhbQ1NSEy5cvw2az4aWXXgKgXUsB2RY+OjrCxMQEOjo6FH8ONbn78nEQQzFRW4+tBl/4vB8A8OefW5R8/b33Tqr2nEoLWZ7nsb6+jnA4jLGxMYnfcSksFou41d7b2wtAauMWjUYRDoeRTqfhdDolLQp69Z9WOmiWSqXEvxdaiBo58MEUs5VzdHRkVmZVxhSzBkSPadlSlVlBEEQbqc7OTlmbrWpoJGsuMtyVTqcxNTUlrtRZlhUHUtQWscTTd319HcPDw5icnDT0gAotavWOti2n1aAQn/uLgOT/nc1O/PZ/Gy775+VaDdSoxpJ2FGIVp4SokbNxAyBxUtje3kYymYTdbpe0KHg8Hl22vOUELsuyWF9fx+bmJiYmJmQHzaxWq+EDH0wxWznRaNQUsypjilmdqFZAEKGldX9VMbsqcoNzu91FbbaqQQ9rLqXFLMuyWFlZKTjcBRwPyL366qvitqzP51NUZNKhB11dXarZJekFEbVPBUrfZAv1zaqdBkaqsqX4u0+P/Pxv8sOeTy4UXyT+zx/bFBeymUwGgUAA2WwWFy5cgNutfopboaADIuyCwaDopECEXUtLiy5BB5FIBAsLC+JCnjy/3KAZ3T4EGC/wwbQeqxyzzUB9Gududkogjgb1IETi8Tj8/uMb9Llz51Sx4TGyNRfZjl1dXcXQ0FDR4a6bN28ikUggGo1ifX1dHBIh0+C13KSJHVpTU1PZoQdG5c7J4+NWjqitN05EbHHeNJ0vcp9ccIjVWSWFLM/zWFtbw+bmpjjAqScOhwMdHR2SthiO40SBSwaseJ6XVC5LBR1USzabFV1aCvUN0/8l1DpoVijwgfThksAHQRDgdrvLDnwol0YWs2r1zA4MDCj6mCZS9FdEp5RqLwZ6es0S0uk0FhcXkUgkMDU1pWretF6V2VoGwOiWizNnzuCOO+6QXBy0STKlAAAgAElEQVTlhrusVmueWTtJIyokcMnNqZDAzWQyEju0lpaWqn8no0GL2nromy1VlS1XyBbiROAq97seHBwgEAiI8cX1urVss9kKDlhFo1ExZZBlWbjdbslnp9oBK9rGbmRkBDMzMxVd05UYNJN7H8jCl37MZDKJeDxeVuCDiXpilrhbmKiDKWZ1hKTFVIKeXrOCIGBhYQH7+/t52+VqYbFYNE3jAmqrzNLDXbktF5UOdxVKI6KN2mOxGABItlndbjfW19c1Cz2oZ4iopfkPvz2v1YCudn7/NanAUdqii6ZWEasG6XQafr8fgiDgtttuM2SefKEBK5LkdXh4iFAoBIZh4HK5JH24Lper6OclkUhgfn4eHo8H165dU6ziW2uiGf0Y9L+Rgbuenh7xfSgU+EBbhTVi4EM5sCyruIuEac2lPqaYNRh6VGaJzVYymYTL5ZJsl6uNHhfTagR0KpUSbYqmp6cl1RElHQrkKrjEzzMSiWBxcRGRSETchkyn04hEIkUruKcFMvzm2F/HyMgIenp6ZI/Dfzp3HNKRK2qrRa4q+8A9O/D5fAiHw6KA0Nu7k+d5rK6uYmtrCxMTE5IezUaA9JR6PJ6Cwo52UsiN7OV5HisrKzg4OMhL51OLYoEPZHcnV+SWM2hWKPCBvA97e3uSwAda4DY6asykmGJWfUwxazC0rMwKgoCNjQ0Eg0H09vaivb0dPT09ut901aYSocmyLJaXl7G3t4fJyUmcOXNG8+QuYiW2ubmJ1tZWXLx4ETabTWxR2NzchN/vF/sI9U5k0gOyZd7Z2Vn28JvSohY4qcSy7IAoHFZXV5FIJETbKj0Gmfb39xEIBNDd3a1b8pselBJ20WgUu7u7iEajYBgGPp8PfX194oJXTycF+rnpQbNcF4VKAh9yk93kAh+SySRee+01QwY+lINabgZqtuOZmGJWV6ppM9CiMksm3xcXF9He3o7r16/D6XQiGo2qsgVjROjhruHhYd2Su4qFHsj1z5E+wq2tLQQCAfA8D4/HI3FRaKQbUyqVEocUq90yJ6KW8N1Xip//dKsBqcrmthPY7XbZAR6yAAmHw4jFYhAEIW8IUMnjQ94fi8XS8MOBlUCEncfjQTQaRUtLC8bHx0WRu7q6ing8Li5AyulhVxO1Bs1yAx+y2Sxu3bqFwcFBQwY+lINaPbNmZVZdGueudUqw2+3IZDKlv7FKSDRlc3MzLl26JLn56zl8Vi92MPRwV1dXV1nDXWpAYoIjkUjZoQd0HyFJZKIF7vb2dp7AJVVCowlclmURDAaxv7+PyclJRUMh3noh//NXTOCW2xdbqEeaVMY2NzcRi8XE40P3eVbat8nzPILBIHZ2djA5OSmpxplIXRzo98fj8cguQEjvKXFSqPX4KEWtfbi51y+yBW/UwIdyYFlW8QVJIpGo23TFRsFYd6gGo5oPtVptBolEQtyKnp2dlVyoCHqJWb28dXOJRCLw+/1wuVw1D3dVC52+NDw8XHVMMEFuUIaO2iST4BzHiZPget+gi0FPmQ8MDOD69euabAXLCVwA+IUaB7zkImHJhDrZAieT+rkCyul0yj4m+Zmenp5T1VJQLmRBT1pSigmbQgsQ+vgsLy8jm83C7XbnRfbqQTkCVy7wwWazIZvNyp4vRgl8KAelK7Nk97WefsdGxBSzBkNpQZlOp7G0tIR4PF6ygqWXmCXPq7WYJdVVrYa7Sr0WOvRAqfQlOWiB29fXJz5/rtVRvQlcstjw+XyKTpnXG/SEOoFM6kejUdGCiWEYNDc3S45NMBiEzWYzWwpkyGazYkKfnGdsuRQ6PqRyeXR0hLW1NWQyGTQ1NUlaFPSqXJYzaMZxHDY2NuB0OpHNZssaNKu3wIdyUKtwUu8VaaNjilmDoVRllk6lGh8fx7lz50p+2PSuzGr9nJlMBqFQSNyq1mO4CzgJPXC5XLqJENIb6PV6ZQVuoQphS0uL6qKS+OlmMhnMzs6qEt5R79CT+r29vQBOBFQkEkEwGEQsFoPT6YTH48H6+nrZVlSNjiAI2NzcRCgUwujoKLq7uxV/PwpVLunI3s3NTaRSKdEiixwfvSqXtEg9PDzEwsICenp6RPP/agfN9A58KIXSLW0cx5lVWQ0wxayOVPOBqVVQEvudcDicl0ql9nNXi9Zilud5MAyDZ599FiMjI5icnJQMd9HbcWqKWFI1T6fTmJycrLvQA1rgEugK4d7eHlZWVsQtVrqCW2gLvBJ4nkcoFML29vap99MtRDweRygUQl9fH65evQqLxYJMJoNoNCqxompqapIIKCP0NipBPB7H/Pw8vF6v5tV8i8UCl8sFl8slSVajt+Z3d3eRTCYluyVkEFALgURXqy9evFhwgLJYHy6p4J7WwAcyQGiiLqaYNRjVCkpSfVhZWUFPTw9uv/32irdS7HY7GIap+LlrRasUMEEQxC10ALh06VLekIMWw10cxyEUChky9KBQhZDeAs8VuOQGXa7AJUN4y8vLZt9nAUgPvMPhwOXLlyX9mURA0VZUtMDd2tpCMpmEw+GQHJ9GMtHnOA7Ly8s4OjrKax3Sm2IWWdFoFGtra5I0QDqyV6ntcXItXF5eLurJTFB60Iz8W6HAB3rort4DHyKRiCaexKcdU8zqSDUfNqvVWpGdlyAIoodkW1ubaLNVDTabTbfKrNrPG4lEsLCwALfbjStXrmBhYUHzlgJ6u7O/v79hRFoxgRuLxXBwcIBgMCgZkiFVmtxzNR6Pw+/3o6mpKU+kmRwLBWLsPzU1VbYdUFNTE7q6umQrhKSNhJjo0xVcj8djuHOUtMT09/fj2rVrdSN6ipFrkQWcOF3kWu3lRvZWer1Pp9OYn5+Hw+HA1atXq75f1DJoVijRjPYFljtX4/F4wcAHj8dTsg9XDe9g05ZLG0wx28CQgZimpiZcvHix5vSWRmwzID6b2WxW4uJABDTHcZr0xR4cHGBxcRGtra0NPbxEKJTGlEqlEI1GJXGjzc3N8Hg8iMfjYBgGMzMzZqUjB7qSRlwcaj1X5SqE2WxW3AIPBoNIJBK6bYFXCvmsW63WhlgI0U4XBNLHHovFJLsgxAOWiFy5rXlBELC2toaNjQ3V7NqKDZqRgkEhP9xCg2ZA+YEPAMSefrnAB7U8Zs3rlfqYYlZHarnZFGtSTyQSCAQC4DhO0S00PcWs0s9LfFoPDg4wMTEhWeWTHq/t7W0IglDWir5aSOgBgJomqBsBekiGCFyO4xAMBrGxsSEGBrz22muSm7OeNkf1AKlWu1yumipp5eBwONDR0SFxPSm2BU6HPeg1nU7H9Da6py7dx07vgqTTaUSjUUQiEayvr0v6pH0+H6xWK4LBoBiSo+WxKjfwodJBs0LVbCL25QIf1CgimJVZbTDFrAGxWq3geT7vgpPJZLC0tIRoNKrKRVtPay6lKrPEDH19fT3Pp5Xe9hocHMTOzg5CoRASiYRke7WlpQUej6emxUg1oQenDTqC9vWvf714vtM3Z9rmyOVySYbMGt16ikQpk75Pvao/cqKBDhMgVTE94pSPjo6wsLAg2tnVY8VYbeiteeKkABzfL46OjsQ4ZYfDgaOjIywuLorHR882kkr7cMsZNJPz1aZt0/b39xGPx/HTn/5UIvZrCXwwxaw2mGLWgBB7LvIhp222xsbGMDs7q8p2uJ6V2VoHz+jhrrNnz+YNwOUOd7ndboyMjIj/TrZXo9EolpeXxZ4sIp7KHZBROvSgEaGr1XIRtHI359zqU67ApY3qjf5+08EQg4ODmJycrLvfqVCYAJ02t7i4CI7jVEnLYhhG9IZ+3eteV3OLVSOSSCSwsrKCvr4+DA4OwmKxFGwjIVvyelfZ1Rg0o3eEnE4nHA4HJiYmFAt8ODo6EqvkJuphilkdqfYGREQlXWUcHBysyGarGvTwewVqr8ySRB8y3FVNcpfc9mo2m0U0GhUHZEh1Q24CnJ7AP3v2rKqhB0allgjaYgKXLELW19clRvV0i0K9icFCxONxcVDRaL3VhdLm5NLManG62NjYwOrqKsbGxnD27FnDHFutIEKfYZg8uy256xzHcaKoC4fDiMViEAQhz0mhniN7yx00Iz2zSgY+xGIxzMzMqP4+nHZMMaszROhUgs1mw9bWFnZ2dmSrjGpRqZOCUlTbM0sqfCzL5kX0KuFQ4HA48oYO6AnwnZ0d0SOSDDJNT0+jra3NvMFS0C4Og4ODuHHjhiLvDy1wiQ0VMaonixDaZzW3RaGejhFpS4lGo3VnJVULxdLMiNMFPQhYbIiJeMb6fD5cv35d9/jreoOu6Fci9G02W8HeU7lEQHoYUM3+7WJUO2jGMIzYxldL4MP6+jq+9rWv4XWvex02NjZw48YNRX6v73//+/j7v/978dh9+MMfVuRxGwFLheJEeyXT4DAMU5FA3N/fx8svv4zW1lacP39e88GXH//4x3j961+v6XOSbeMLFy6U9f30cBdJ7iJomdxFQg+SySR6enrESm4qlYLT6ZRUB+tNPGkFcdxoaWnB2NiYLtUdWuCShUhukIBex4gW+sPDw+jt7T2V5wndRkKOEamye71eJJNJZDIZ0+miAKlUCnNzc3C5XJicnFTlc0YvQshxYhgGLpdLsgipt2sdEbb7+/tYWlrC+Pi4ZLFYatBMDoZhcOvWLfzsZz/DN7/5TbAsC4ZhMDIygsuXL+Py5cu48847JfemUiSTSdx222149dVX0dTUhHe84x2499578Za3vKXi39lAlH2imEtXnSm3MhuNRkUT9N7eXrS2tp6aCe5yK7N0ulmx4S61k7vIBD6JCqZjcAm0eCIxlvUgnrQinU5jcXERDMPoHkFLJzHJBQlEo1FsbGwgnU5LFiFqJ2XFYjEsLCzokk5VbxRqI9nY2MDy8jK8Xi+cTidee+018RiRz9JpSTOTg3ZymJ6ellQUlaaQ3R5p9aET55xOp6SCq2fIAcdxYn/15cuX4XK5JJVbuvhRrpOC0+nE1atXcfXqVTzxxBP47Gc/i5GREYRCIbzwwgt47rnn0NHRgbvuuqvs1/n0009jeHhYvO/feeed+Pa3v93oYrZsTDFb55Ct8mw2i8nJSbS2tmJ1dRXZbFa316R0dnUpSvXMCoKA7e1tsR+11HCXWn3FlYQeyJnUy4knI/d3ysFxHFZXV7G9vV1Q6NcLxY4RvQhRWjxls1ksLS0hHo9jenpa0h5jckwqlcLCwgLsdjtu3LghWdhnMhnJ4A5JM8sNe6jX804potEo5ufn0dnZqbndFkGu1Qc4rlySz1FuIAc5Tlo4Kezu7mJxcTFv10PJQbNIJIL29nZYLBaMjIxgZGQEv/Irv1Lxa93Z2ZFcC1paWrCzs1Px4zQqppitUxiGwdLSEo6OjvK2yh0OB1KplC6viwyfaVklKjZ4Rqx3PB4Prl69KrmpadlSoEToQa54yu3vJANMRrSgapQI2kJJWeQYbW1tiQKXFk/lVJ7o4aWRkRFMT083vOCqFLrSODU1JTskWGhwpx7EkxZwHIelpSVEIhGcO3dO112PQjidTpw5c0Z2uCoajYqWiADy7NyUEOXZbBYLCwvgOA5Xrlwpa5ezWB8uKZbIDZrt7+8rcgzOnj2LWCwm/n80GpUsEE47ppjVmdybFcuyCIVC2NrawtjYGGZmZvK+x26361aZrRcxm0wm4ff7wXEczp07p/hwV7mQgAqLxYILFy4oagEkt/1NC1w5C6p6DBEgE/gul6shkpdykbsx05Unujoo53QBnPQOt7a2msNLBTg8PITf7xfdQCoRnnLDmizLiv2doVAI8XhcHEgjx0lPG6pq2NvbQyAQwMDAQF1athWj0HAVcQ/Y2NgQ/YprsXMju3hjY2MS391qkAt8IPedo6Mj/OEf/qEodGvl5s2bCIVCYq/4U089hXvvvbfmx20UzAEwnaEjU9fX17G2toaBgQEMDg4WvFgfHR0hHA7j/PnzGr9a4OWXX8bo6KjmW59k8IxswR4eHmJqakpyc9JSxNKhB5OTk6r2opWCHo4hf8j0Ny1wtZ4sJscqFothamrq1A/m0E4X0WhUrA6Smx3ZgTGSANEC2kpqenpaVc9Y2oYqGo3mpZkpWR1UEoZhsLCwAJ7nMT09bYjdmmqhU7zIn2w2m+ekkLtoZhgG8/PzsFgsmJ6eVu16KAgC/u3f/g0PPfQQ3ve+9+G3fuu3FKv4/+u//isef/xxdHV1weFwnAY3g7IvhqaY1RmWZREOh7G8vIyuri6Mjo6WrMrE43EsLS3h4sWLGr3KE1577TX09fVpnmjy1FNPob+/H+FwGCMjI+jr69NluIt4+25sbGBkZAQ9PT11KT4KCdxq/Tsrged5hMNhrK+v1/V7pCeCIIiL166uLtjtdsRisbwwjtPS3ymHIAgIh8NYW1vT1TOW5/k8gUvSzOjqoB7VdLpPf3x8/NRuO9MpXmRHhFQwfT4fOI4T/avVfI+Ojo7wB3/wB9jZ2cFf/uVfYmBgQLXnOiWYYtYorK+vi1Pv5W6/ZjIZ3Lp1C9euXVP51eWzsLCAzs7OiixFaoEMd7388ssYHx/HyMiIpCqSO9yl1s0uN/RgeHi47qozpSAXfFrgkooGXcGtpYVkf38fi4uLOHPmTN6xMjmGhHi0t7fLLl7p/k66gksvQhpd4MZiMczPz6OlpQXj4+N113ZB+6wSoUt8VunjpGY7VjKZxNzcHDweDyYmJuruPdIbQRAQjUYxNzcH4LgdKJPJqDIMKAgCvve97+HDH/4wPvCBD+A3fuM3GqL/ug4wxaxR4Hm+4v5XjuPw7LPP4o477lDpVRVmaWlJYr2iJqRHzuv14vDwEG94wxvEf9OypSAajSIQCMDlcmFiYqKhej6JNyQtcFmWhcfjkVQHS92USQ+z1WrF5ORkXgStiTRidXp6Gh6Pp+yfpeOUaYFLW7mVE61Z77AsK7bvzMzMGMrJQRAEcfubiFx6+1updh+e5xEKhbCzsyOGsJhIoYcpc9vR6Jha8lmi0+lIZG+5n6XDw0N88IMfxNHRET7/+c+jv79frV/rNGKKWaNQjZgVBAFPP/205uEFABAKhWCz2VTdPqGHu6anp+H1evH000/j9ttvh8Vi0TT0YHFxEZlMBlNTU4a6sdaCnMClq07kDxkGXFlZweHhoe69w/UK6YcPh8MYHx9HV1eXIucsLXBjsRgSiYRhJ/TJzsfS0hIGBwfR39/fEJVnejeEHCsSJEBXcMu13ItEIpifn0dXVxdGRkYMcWy1hgREuN3usivWLMuKTgqxWEzSK01H9uZaPn7nO9/BRz7yETz44IO45557zOOhPKaYNQrViFlAnyQuAAiHw8hmsxgZGVH8sWk7stzV9DPPPIPbbrtN3LbWO/TgtEGqTrTAzWQyYFkWHR0dGBwcFAWuyQmHh4cIBALo6OjA6Oio6m0X9IR+NBpFIpEQq05kEVJvAjeVSmF+fh4OhwNTU1O6RaBqBR0kQMQT7SlNjhUdmsKyrOg9PDMzU1FV/7RA+tDD4bAiARE8z0sEbiwWw0c+8hE4HA7MzMyIO1GPPfYY+vr6FPotTHIwxaxREAQBDMNU/HN6idnt7W3EYjFMTEwo9phk24wMVckNd926dQsMw6CtrQ2tra3w+XyK3/ToramBgQH09/fX1U2/Xjg6OkIgEIDP50N3d7ekD5cMxtAtCqexbzaTyYhhJ2pP4JeCFrik6lTLtqpS0Nvlk5OTsp6xpwViuUcfJ+JXbLfbEYlEMDAwYFZjC5BIJDA3Nyf2WKt1zclms/irv/orPP7442htbUU6ncb+/j5GR0dx5coV3HnnnWYil7KYYtYoVCtmyba71he2/f197O3tYXp6uubHEgQBW1tbopF+seEuAHnT+SzLym59VwMJPWhra8Po6Oipjg4tBGm7yGazmJqakq0O0YMx5KZ8mgQucbvY3NwUWwrqEXpblUzo0x6ragvcg4MDBAIBcZjSFGj5ZDIZzM3NIZvNoq2tDclkEqlUKm8YsBF6patFEASEQiFsb29jZmZGVfu/g4MDPPjgg8hkMviLv/gLSWRvMBjE888/j3g8jt/8zd9U7TWcQkwxayQymUzFP/Pss8/i4sWLmm/JRSIRrK+v1+xxS4a7fD5fnpNDucNdpLczEomIwonjuIqEEx16MDk5qWsFrV7JjaCtVKDR23W0tRG99W00c3o5iEDr6uoypNsF8VgtJHBJJbcW4cQwDPx+P7LZLGZmZsxBQRloS7KJiYm8z5tcr7TVas1zu2h0gRuPxzE3Nye28KgZU/6tb30LH/vYx/DBD34Q73rXu05925mGmGLWSDAMU3FCyAsvvKDL9mWtHreJRAJ+vx+CIGBqakoS86eEQ4FcZVAQhDyBS6amo9GoObhUAEEQsLOzg5WVFfT09GBoaEixG0audyeJacw9Tka4IafTafj9ftGwvpEEWqEQgdwWhVLCnRZoSg7BNRpku5ws8svdaSKtJPRxslgsEguqRlgwAsfXjmAwiL29PczOzqo6mLu3t4cHH3wQHMfhc5/7XM2JYSYVY4pZI1GNmH3llVcwODioeapSOp3Gq6++iqtXr1b0c2S4iyRmaZncRYQTiYA9ODgQt+66u7vR2tp6KioZlRCLxeD3+9Hc3FyRB3ItkOhKujIIIK+CWy/HifR8bm9vY2JiQjPvZb0pdJxyWxSIcCKesa2trRgbGzOHBGWgBdr09LQi1/Vix4kWuUYSuNFoVHRzULM9RRAE/NM//RMefvhhPPTQQ/i1X/s1c/GlD6aYNRLViFnygaZFoRawLIvnnnsOt99+e1nfT7aoNzY2MDo6it7eXslwF/keLUMPuru70d/fL7GfisfjkuQl0ot22i5gZNGRSCQwNTWFlpYWXV8PvfVNKk/08JJeC5H9/X0EAgF0d3ebPZ+QCidynOhF6tjYGLq7uw0lnLTi6OgICwsL6O7uVnT3Qw65CX2e50VfafK5qreZAY7jRAvA2dlZyY6e0uzu7uKBBx6A1WrFZz/72VObqlYnmGLWSGSzWbEqWS5ahhfQlOtxSw939fb25vUQapXcBRyv5v1+P9xud9Eqo5wxvd1uF8Vta2urxC6nkaC9UEdHR9Hd3V23v2eh3k4t7KdSqRT8fj8sFgumpqbgcrkUfw6jQ9pTlpaWcPbsWTQ1NYkuCqTlx6iVQSXJZrNYXFxEKpXCzMyMbv36pDWLXjQSX2n6OOllmXZ0dIT5+Xn09vZiaGhI1YLHP/7jP+LjH/84PvShD+Gd73xn3V4DTxGmmDUS1YhZLcILClHKFuzg4AB+vx8tLS2YmJiQXAS1TO4i0/cMw2BycrKq3iqGYSQOCqlUSvSDJH+MLmgaIYJWzl81NyGrlthKjuMkNlJa74gYhWQyiYWFBTidTkxOTuYJoELDgKfF7YJAxP7w8LBkt6peoINTyOeKTjOjwx7UguM4LC4uIh6PY3Z2VlWxv7Ozg/vvvx9OpxOf+cxn6taF5BRiilkjwbIsOI6r6Gc2NjaQyWQwOjqq0qsqTCExq/ZwV7mwLCv2n6kRepDJZMSbcSQSQSaTERN9WltbFYms1IJGj6BlWVZyM65W4JJkKqWH4BoJ0vO5u7uLqampigYqC21951ZwG6HXNp1OY35+Hna73XABESTNjK7g0te+StPMikEKIv39/RgYGFC1GvvNb34TjzzyCP7oj/4Iv/qrv1p3C4tTjilmjUQ1YnZnZ0ccptKaXDHLMAwWFxcRjUYxNTUlMT/XUsTqFXpAEn3oCi7DMHkeuPXSh3aaI2hzW0kSiYSklYTulSZi32azYXJy0vAVeLUgwkNJsV/Ir5j0dhpN4NLpVI1U2S+WZkYvRJqbm8u67rMsi0AggFQqhdnZWVUX2Nvb2/jABz4Aj8eDRx999NQMcBoMU8waiWrE7MHBAba3tzE7O6vSqyoMCWwQBKEuhruA463ypaUltLe3Y2RkRHfhSG/TkT8cx+l6MxYEAZubmwiFQhgcHER/f79ZhcCxwKWPUzKZBMuy4HkeAwMD6OnpOZXDgKUgKWcsy2piSUYLXCKeiMClq+31JnCJH2pra6uq6VT1BNm9IscplUrB4XDkhT3Qn6m9vT0EAgHVWy94nsfjjz+OT33qU/jjP/5j3H333eZnu34xxayR4DgOLMtW9DOxWAwrKyu47bbbVHpVhXnmmWfQ09ODtbU19PX1YWhoKG+4i1Rj1RaxpLWBVM/qeatcEARJtYmOfyXtCWp5QR4dHcHv95sJZ0XIdbzwer3i9ncymYTT6ZSIpnKrTY0GqTKur69jfHxc12lvnucli0Z6eIleNOpxvpMJ/IODA8zMzOjuDKI3DMNIKrjJZBI2mw0ejweJRAIWiwUXLlxQdQdka2sL73//+9HS0oJHH31U1Qr51tYWHnroIbz00kt49tlnAQCf+MQnsLW1hZ6eHjz33HP44z/+Y8zMzKj2GhqAsi+w9bWENSkbu91esQBWgoODA8RiMbhcLly/fl234S6GYbC8vIxYLIbJyUm0tbWp8jxKYrFY4PV64fV60dfXB0DaLxgOh8XwAKW8VekI2vPnz8tG0JqcLIocDgcuX74sDrbQgyD0MODW1hZSqRScTmfeMGAjC9xoNIqFhQW0tbXhxo0bulcZSUIZ/ZmiF41k0IoWuOSzpabAJa0Xvb29uHbtmtlnDcDpdKKzs1MiIDc3N8UYcQB48cUXJdZ7SnlL8zyPv/u7v8Of/dmf4WMf+xje/va3q/45/dGPfoS7774bL774ovi1eDyOT33qU7BYLPjbv/1bPPjgg/jnf/5nVV/HacEUs3VANR8qh8OBbDarwquRJ5FIYGFhARaLBR0dHRgZGRGFrJYilud5rK6uYnNzEyMjI5ienja0eCAxlHTVhnh2RiIRrK6uitZTtGgqNbhET99XE0F7WqCrZ1NTU0UXRU6nE2fOnJH01tHDgJubmxK3C3IzbgSBy7IslpaWEFYjK3kAACAASURBVIvFVPf5rBW5RSMRuLFYDHt7e1heXgbLsnktCrUK3Gw2i0AggEwmg4sXL9b1TpGeMAyD+fl5AMDtt98uKYqwLCsu8NfW1qpOnSNsbW3hd3/3d9HR0YEnn3xSMtOhJu985zvxxBNPSL72J3/yJ+Lfya6ciTKYYtag2Gy2ivtsq4Ee7pqenkZ7ezvm5ubAsqzmw10kWrW7u7suqkJqYbPZ0NraKkkBoq2nVlZWxMn83MElAOL71Nvbixs3bphVIRnI+bS8vIyBgQFcv369qnO3qakJXV1dksUCLXA3NjbEgRj6WCkx8a0F9Ps0NDSEqakpQ7zuXGiB29vbC0Da1763t4eVlRXRfopuUSjHcUAQBGxvb2NlZaXufZr1hH6fCrWo2O12tLW1SRaWdChHOBwWPYtzwx7ofmme5/GNb3wDn/nMZ/Dwww/jbW97W90cE4Zh8JWvfAWf+9zn9H4pDYMpZuuAaj5gan8oSWVvc3MTY2NjmJ2dFZ/TZrOJQ2s8z8Nqtar6eiKRCAKBANxut2QL+DRht9vR3t4ucR6gB5d2dnYQj8fBMAxcLheGhobQ0dFRNxfveiIej8Pv98PlcuHq1auK2yPlClxBECQCd319XWJpRAvceiKZTGJ+fl6190lvLBYLPB4PPB6PrMDd39/PE7ikMki/F6lUCvPz83A6nbh27ZrZj16ATCaDubk5OByOit8nuQU+adGKxWLY2tqC3+/H+9//fnR3d2N6ehrPPfcchoeH8eSTT9aVYwvDMHjPe96Dj33sYxgfH9f75TQMppg1kUAm3ldWVtDX14ebN29KKnuCIMDlciEQCKCzs1McXFKjaZ8OPZienq4q9KCRcTgc6OzshM/nE6t/MzMzEAQBkUgE8/Pz4tfJcapH0aQVLMtieXkZR0dHmJ6eltwY1cRiscDlcsHlcomVKFrgRiIRrK2t1Y3ApT1jp6enDdGPrhTFBG4sFsPBwQGCwSCy2Syam5vF9oXJyUl0d3fr/OrrE9pFZXJyUjELLLr1qr+/HwDw7//+7/jzP/9zfPe738WZM2cQDofx5je/GVNTU7hy5Qre+MY3lkyvVJNUKoV7770XDzzwAM6fP49vfvObeMc73qHb62kkTDeDOkAQBDAMU/HP/fjHP8bNmzcVq76RvHliIVNsuItMpkYiEUSjUWQyGTQ3N0uCA6qtUJDQg/39fYyPj6Ozs9OsMMpQTgRtblUw91iRP41WdaMh0crBYLCuLckK+RVreazINcAMiChONBrFq6++iubmZjQ3N4u7IuRYaZGQZQRSqRTm5ubQ3NyMyclJVW3TwuEwfud3fgf9/f345Cc/KS7CeJ5HIBDA888/D57ncc8996j2GmiefPJJfPWrX8V3vvMdvOc978H999+Pe+65B6+88orYy51IJESnAxNZTGsuo5HJZCr+mWeeeQaXL1+ueVuLbLuSvHl64r3cvliSDkPfiMmABRG4pWIq9Qo9MCJEdHR1dVUcQUtEE1mIkKhK2gO3Hv06qyEej2NhYQFutxsTExOG2wLOTV2SC+Qot6+zGJlMBn6/HzzPY3p62gyIKADHcWJ1f2ZmRrJbVOhY1UO1XWvokIjcIB2l4XkeX//61/H5z38en/jEJ/DWt761LherJlVhilmjwTAMKjwWeP7552tKSclkMuKEcm4EJRGxgiBUHXpAtuCIaIrFYhAEQdZ2an9/H4uLi6JTgtFEh1YQCym73a5oKlWhkAev1ysRTUYZustms1heXhYHFxvJ41Nu4Zg7uFTuzggtOkzXi+KQBWRfXx8GBwfLuh7mVttzI2DJ56qRFg/JZBJzc3Pwer2YmJhQ9Zqxvr6O++67D8PDw3jkkUc0ax0y0QxTzBqNasTsyy+/jNHR0Yp7STmOQzAYxNbWFsbGxtDT06NZchfP82Llgm5RcDgcGBwcxJkzZ8y0JRnofk+tImjlIkUFQcgTuPVUPaf789ROEqon5BYj9M6IXHhANBrF/Pw82tvbMTY2ZpiFitYwDAO/3w+WZTEzM1Oz8KQFLrkWEoFLL/SN4nhBIImQm5ubmJmZUbXXmud5fOUrX8EXv/hFPPLII/jFX/xFQ71XJmVjilmjkc1mxa38cpmbm0N3d3fZWzhkGz8YDKKvrw/Dw8N5w110chegnmsCHXowNjYGi8UiClyStkQu6q2trYa7sCsF3XoxNDSEvr4+Xd8HejESjUYRj8dhsVgkN2GPx6OLwI3FYpifn4fP58P4+Pipr+4XqrY3Nzcjk8mA4zjMzs6eqgGvSqB7rcfGxnD27FlVrQfletuNYulGInvb29sxOjqq6sJodXUV9913H8bHx/HII4+Yg8GNjSlmjUY1YpYMa5UTJ7m/vy/GmZYa7tIq9KCYHyPDMJKeznQ6DZfLJZnKb+ShJcA4EbQcx+UJXJvNBp/PJx4vNavt2WwWS0tLiMfjputFEYg4W1paQkdHB6xWqxj/mlvBbYR+6Vogg0sulwuTk5O6fPZyBW4sFpN4FtdDKAfP8wiFQtjd3VU9spfneXz5y1/GY489hj/90z/FW97ylroU9iaKYopZo1GNmA0Gg3A4HKItiRxkAMZms2Fqako01ge0FbG5oQdDQ0NVDS3R7Qn00BIZMGuEm3A6nUYgEADLsnkDeUaBZVlJlSmZTMJut0uqTM3NzTWdb3TVemRkRNIuYyKFJPjJiTO6nYQsSkg6kRH7pWuBLLa3trbEkJh6I51OSxaPRODSuyNaCNxYLIa5uTmcOXMGIyMjqu7GhEIh3HfffZiensYnPvEJMznr9GCKWaNBQggqYX19HRzHYXh4OO/fMpkMFhcXEY/HVRnuqgQSeuDxePKqwrVAZ7CTPzzPSy7q9dbTWQw6gnZiYkIxP8Z6gdi5kQUJHf1a6TZqJBKB3+9Ha2srxsbGGmIRowakP35vb68iz1i5fulGF7ikh7izsxOjo6OGuW4AyKvgplIpSauWz+erefFI4Hkey8vLODw8VD3amOd5fOlLX8KXv/xlfOpTn8Kb3/xmc8F6ujDFrNGoRsxubW0hkUhIUkTo4a7x8XHJNr7aw125pFIpLC4uIpvNYmpqSpPVNEmFIdVb0tNJCyaPx1NXF0Q6MrS/vx8DAwOGupHWQm6fIGknoful6cUPiVdOpVKYnp42KzRFINP3vb29GBwcrPmcIp8tup0kdyDQ6/UaTuByHIfFxUXEYjHMzMw0zDlFPltkAUkLXLLgr1TgkjAWsrum5nVqZWUF9913H86fP4+Pf/zjhtyhMqkZU8waDY7jwLJsRT+zv78v9irRw139/f15Fxoth7tyQw/0rjCyLCsJeKC3vOkEMz0EbiwWg9/vR3NzMyYmJhq+D7gUxYIDAIgDg3oPwtUzmUwGCwsLEARBdc9YMhBIBFMsFgMA+Hw+UTDV8+7I3t4eFhcXRV/rRj+nGIaRVHCTySQcDoekgivX385xHJaWlhCNRjE7O6uqsOQ4Do899hi++tWv4tFHH8Ub3/jGhj8uJgUxxazRqEbMkhjM3t5e+P1+tLe3501xa90XGw6Hsba2hsHBQfT19dXtTYy+qEcikZIVQTWen1QYp6amzKGlIhweHmJ+fh4ul0tMW2JZFm63W1yMNEq/dC0IgoC1tTVsbGzo6hnLcVxeBReArL+0XjAMg4WFBfA8j5mZmVMRZFAIci0kCxJa4JLrUjAYxMDAAAYGBlQVlsvLy7jvvvtw22234eGHH1ZVNG9tbeGhhx7CSy+9JKZwpdNpPPDAA+jv70cgEMDv//7vY2pqSrXXYFISU8waDZ7nkc1mK/qZ3d1d3Lp1Cx0dHboOdwGQhB6Mjo4aTliQyWHaQYEkLdEOCrX+XjzPi4JDbbsfo8MwDAKBADKZDKanp/OS6eT6pRu5p7MYkUgECwsL4uev3n5vOccLq9WquaUbPTQ4Pj5elhPMaYRhGBwdHSEYDCKVSsHhcMDpdEqOl5IOJRzH4Ytf/CK+/vWv49Of/jTe+MY3KvK4xXj88cfR1NSEj3zkI/jZz34GAPj4xz8Oq9WK3/u938OtW7dw77334oc//KHqr8WkIKaYNRqViNlMJoNAIIB4PA6e5/H6179e/Deth7vi8TgCgQDsdjsmJiaqTiOrR2ifzkgkItoYEcHU2tpaUY8g2dI8e/YshoeH605w1As8z+elUpVzDpOhJTpxDqiviqDSEFuyRCJhuB5irQVuIpHA/Pw8PB4PJiYmDLfg1hLSb0122CwWC7LZbF6Lgs1mkyweq5lHWFxcxH333YerV6/iox/9qKQoozZPPPEEHnjgAVHM3nXXXXj44Ydx1113AQBaWlqwvr7eUAmCBqPsk8n8NBsI0ou6vb2N8fFxzM7O4plnngEgP9yl5k2bYRjR23NycrIhjdctFgs8Hg88Hg96e3sBSIdgwuEwYrGYJDSgtbU174JOR9BeunSpoaIrlebw8BB+vx+dnZ24ceNGRYKfCCG6ZYPe8l5bW0MsFoPVaq3rgcByoA39h4eHMT09bbjfwWazoa2tTXLtIP3t0WgUwWAQiURC9Cyu9ngRL9SdnZ2KHB1OI9lsVtwNyb1WORwOdHZ2orOzU/L9RNzu7u6KArec48VxHL7whS/gb/7mb/CZz3wGb3jDGzT5HYuxs7MjuX60tLRgZ2fHFLMGwBSzdUKxizPpRQ2FQujv78fNmzdFoUoqsPRwl5rVWI7jsLa2JoYezMzMGO4mWgu0ECKQClMkEsHKyop4A/Z6vUin0+I2eT16VtYLZLchm83ida97nWLVGZvNhtbWVklmOy2Y6ONFC9x6jlQmFUa3241r167VbZhGNdjtdrS3t0s+K7RnsdzxKlYRJNP3Z8+exfXr1xuqKq80u7u7WFxcrMizuZDAJZ+v5eVlUeA+//zzyGazuHHjBjweD+6//37cuHEDTz31VN3s6J09e1bc0QGO7drMVhRjYIrZOmdvbw+BQAAdHR24ceNG3nAXx3HY3t4WE7G0CD3o6empuGrWyORWmMggTigUgs/ng8vlwvz8vOipSnpwT/PQCYH0EG9ubmo2tCQnmOgt1J2dnbxIZb2TloDjRdPKygoODg4wPT0tEeiNjN1uR0dHhyS2mxZMdEWQrgaGw2Ekk0lcuHDBtHUqAhmGEwQBV69erXnw1eFwyB6vdDqN73//+/jgBz8Iv9+PgYEBZDIZfOMb38DVq1dx7tw53Vs/3va2t+Hpp5/GXXfdhVu3buHixYtmVdYgmD2zdUQmkxH/HovFsLCwAIfDgcnJyYLDXQcHBzg4OEA0GgXLsvB4PJIJbyUEJzGo93q9ioYeNCKHh4cIBAJiRjl9caYtpyKRiDhgRgumRqqyleLg4ACBQABdXV112UMs53hBhzy0trZqtiAh/db/f3t3HhxlneYB/Nu5OncC5CTkTro7IAm5AB3RGR2wLGZEZYvRnVmWmhpLhU1AQC4ZERwiGmRQJgg4zAHssLqKziqDrieLSk4CBOhO54SEkDvpI+m73/2Det95OwmQkLzdb3eeTxVVg4P2r4/Qz/u8zzF9+vRJNYd4LNgLkhs3bqCzsxM+Pj7Dfr4manGAp+jo6EBjYyNSUlIQHR0t6GOpVCoUFhbivvvuw/bt22GxWHD+/HlUVVWhqqoKSqUSJ0+eRExMjKDnYJ0+fRpHjhzBZ599hueffx7r1q0DAKxfvx6xsbGor6/Hli1baJqBa1EDmDsym83cooHBwUHIZDKH+q47NXfxt/awDUtsPScb4I6l3ow9i9VqRXp6uls1lzgbu4LWZrMhPT19VJkghmFgMBgcJijYbDZBLkjExGg0Qq1Wg2EYyGQy0dxiHI2hM3BNJhMCAgIcAqaJvNhjXysAkMlkVG99GyaTCSqVCl5eXpDJZJBKpQ5b59ixU+NdHOAJ2NfK29sbcrlc0Itoq9WKP/zhDzhx4gRKSkowb948wR6LeBwKZt3RlStXuOYu/sim8Wzu4tdzajQaDAwMwNfXlwuWwsLChn1BWq1W7nZmWlqaQz0UccRuXOvq6pqQFbQjXZAAGNZg5o6ZObYRp6Ojw2PW9d5qyUNQUJBDTedYgwV2okNbW5vHvFZC4c+3Tk9Pv+Nrxc+4D92MJZaSEqHwGwfT0tIEL+tRKpUoLCzEAw88gG3bttHFGBkrCmbd0Y0bNxAeHi745i6z2cxlAzUajUN2yWKxoKenBwkJCaJeeuBqDMOgo6MDTU1Ngq+gHWmEkTs1LAH/HPUTHR2NxMREj/5c8Ue6Dc24sxckt8u4i31mrJgMDAxAqVQiJCQEqampd11zOdJaZX5JCVv7LuafsTsxGo1QKpWQSqWQyWSC1qdarVa8/fbb+Pvf/46SkhLMnTtXsMciHo2CWXdksVi4JQfO3tx148YNNDY2wtfXFxKJhBtAz7/d7ckByFhotVqo1WoEBQW5rIaYbYDhr+j18/NzWPAghiyIwWCAWq2GRCKZ1LfJ+Rl3dpQRwzAOSx78/f257m+FQkFNS7dht9vR1NSEnp4ewZrhjEajw0Xk0ACXbeIUe4DLZq5bW1uRnp4u+J22K1euoKCgAA899BBefvllanQl40HBrDuyWCyw2WxO3dyl1+uhVqvh6+vrsPSAP4Beo9FAr9dDIpE4NL+IPRs40cS+gpbNLrEBLj/jzga5zmows9ls3GxPZ3yBuiN2ZrFGo0FHRwc0Gg2kUimmTp3qUONOF5GO+vr6UFtbi5iYGCQkJDjt9WG3BA6tmeavwRbblBKDwYArV64gODgYaWlpgmb5LRYL9u7di5MnT2L//v3Iy8sT7LHIpEHBrDu6cOECEhISuOyokIEif+mBTCYbVWaDnc/JBksDAwMO2UBndnc7E398VHJystusoGXrOfkNZuzEC/6X70R/wXV1daGhocHpwYY74s+MTUtLg5eX14glJeNZGuApLBYLdzGpUCicuinqVtifMf57JoYAlx0P2NbWBoVCIfiiiMuXL6OgoAALFy7E1q1bPfJ7gLgEBbPuhmEY/OY3v0F1dTX8/f2RnZ2NvLw85OXlITk5ecICApvNhmvXrqGjo2NCArORsoHsOBw2yHX17MDx8LQVtAzDDFv5yt7uZt+vu135Ojg4iNraWvj4+CA9PX3SlhSMxlhmxvKXBrAlJT4+PpNm5BQ747qxsXFMA/1d5VZNgUJOveBj64jDwsKQkpIieDZ2z549OHXqFA4cOICcnBzBHotMShTMuiuGYdDf34+KigqUlZWhvLwczc3NmD59OnJzc5Gfn4/c3FxMmzZtTH+h8xuWYmNjER8fL8hfcvzmFzZgstvtDt34dxssORO7gpYtv/DkwMxut3OZJbakhL/p7E4lJexEh+7ubshkMtp0dgds5nr69OmIj4+/q8CMv+ThVjXT7lDPeSdGoxEqlQo+Pj6QyWRuO+OaHcPHXkCyAS5/Dm5ISMi4np/dbucSFQqFQvClGjU1NSgsLMSjjz6KLVu2uO17Q0SNgllPwt7mLi0tRXl5OSoqKqDRaCCXy7kANysr65bdtn19faivr0dISAhSUlKc/pcOvzaQ/cuc340fFhYmmsySxWJBY2MjNBrNsDm/k8nQbCBbUjL01ml3dzcaGxtpmP8oGI1G1NbWCtYMN1JHPv92d1hYmNsEHAzDoLW1FdevX/fYmmt+gMv+slgsd7VIRafTQalUYtq0aRN6J28kZrMZb775Jr744gscOHAAc+bMEeyxyKRHwayns1qtuHz5MkpLS1FRUYHz58/Dy8sLc+bMQW5uLvLy8sAwDLZs2YL7778fzz33nKiWHrDBEr8bn7/u1dlfvPxZlYmJiYiNjRVFcC0m/JFufX190Gq18PHxQUxMDKZOnSrorVN3xq+5dmZgxjYs8Wum3WHrnF6vh1KpRHh4uOC3ycVm6Fg3nU4Hq9U6LIPLvmf8qQ4ZGRmCN6VevHgRhYWF+NnPfoZNmzY57ee9uLgYzc3NiIiIQF1dHQ4fPuxWy1bIXaNgdrJhGAZ6vR5VVVU4ffo0jh8/jr6+PmRlZSErKwt5eXnIz89HdHS0aIO0kda9Dp3NKUT97e1W0BJHNpsNjY2N6Ovr4+pi+e+ZxWIZ1mA2mV/P/v5+qNVqTJs2DUlJSS4PzEbKBg4Nllz1nvHriJ0RmLkLts6d32Rms9ng5+cHvV6PiIgIpKWlCRpYmkwmFBcX45tvvsGBAweQlZUl2GMN1d7ejpkzZ6K7uxteXl5YsmQJli1bhl/+8pdOOwNxGQpmJyOr1YrDhw9j//79KCgowIoVK9DV1YXy8nIug8tuX2Kzt9nZ2QgODhZlgMtmKfiZJbb+ls3ejmd0kcFgQF1dHex2O2QymSi6o8WK34QzY8YMzJgxY8TPDPvFyw+W+DXTk2VmscViQV1dHYxGI+Ryuahnxg59z3Q6HWw2m8MMXKHXKvf29kKtVo+rjniysNlsaGhoQG9vL6Kjo2Eymbj3bOjmuYm4KDl//jxWr16NJUuWYOPGjU7P5Gu1WshkMqhUKoSHh+Phhx/Gm2++SeUNkwMFs5PR999/j1OnTmHjxo23zGrYbDao1Wqu/ra6uhpmsxmZmZlc/W1GRobobj2y2GYlNsDlb8NiA9w7berhNyzRut470+v1qK2tRUBAwF1lgEaqmfby8uIuSjxp3BS7gOTq1atITk4W9Z2Q2+HPmWZ/zhiGcbgomYhGTovFArVaDbPZDIVCQbeO76C/vx8qlWrEoH+kxRzs8pu7uSgxmUx4/fXX8X//9384ePAgZs+eLdTTuqOjR4/i2LFjiI2NBcMwKCkpEVXZHBEMBbNk9IxGI6qrq7nsLTtkm83e5uXlIT4+XrTZNH5nt0ajgcFg4Bpf2GDJz8/PqStoPYHVanVohpvI7mh2ZjH7ng0dNzWaixKxYYN+djOcWC8I75bNZoNer3eYgSuRSBwmlYz2ooT/s+jOQb+z2Gw21NfXQ6/XIyMjY9R3ke42wD137hzWrFmDpUuXYv369S79LJ8/fx7Lly/HuXPn4OPjg3Xr1sHb2xtvvPGGy85EnIaCWXL3GIZBT08PKioquAC3paUFCQkJyMvLQ25uLnJzcxEeHi7KL6ChjS8ajQYmk4nrFE5OTsbUqVNdXr8oVgzDoL29Hc3NzYiPj0dcXJxT3mez2exwUcKuD+Uv5RBjgxm/jlio1apiZbPZhk294E8qCQ0NHTbWzWAwQKVSQSqVIj093eOC/onGlmDMmDFjQn4W2Tsl/AB3586dCAwMRGZmJlpbW6FWq/Huu+9i1qxZE/Qs7t7JkydRXFyMb7/9FgCwe/duXLt2DW+//bZrD0acgYJZMrHYrtmysjKUlZWhsrISAwMDmDlzJpfBzczMFN3mF3YF7eDgIOLj42Gz2aDRaLhlAfxb3WKtHXYmnU7HZRfT0tJcGmjw14eyFyb8bnwxLOVgZ8aymf7J/vkBbt4p4WfdDQYDfH19ERISwl2wyOVyKu+5A6vVCrVaDZPJhIyMDEFnXRsMBrz//vv429/+xq1Vl0gkyMzM5O7O5ebmuuTzbbPZUFhYCH9/f4SHh+PSpUvYu3cvYmNjnX4W4nQUzBLhmc1m1NTUcAFuTU0N/Pz8kJ2dzdXfpqamuuRWPjtAvL29HSkpKYiMjBz2F7HNZnP40mWzSmztbWhoqNvd6r5b7HxdNtAIDQ119ZFGNHQpx9BmJXYph9BZd3ZmrJeXF2Qymegu4sSmt7cXSqUSfn5+8PHx4bLu/AyuJy8mGavu7m7U1dU5ZUyg0WhEUVERysrKcPDgQcycOZP75xcvXkRlZSWuXLmCffv2TYq/C4moUDBLnI9hGGi1WlRWVnLbyxoaGhATE+NQfztSYDmR2GxZdHQ0EhISxhTYWCwWh/IEdvA8P8D1pNui/IYld52vO7RZSafTAYAgWXf+RZKnDvOfSGwJRn9/PzIyMhyadoaufDWZTE5b+SpWFosFtbW1sNlsUCgUgl8kVVRUYO3atXjqqafwwgsvTOoxekSUKJgl4sAuIygrK+Pqb3t7e5Gens4Ft9nZ2ROyAUyIFbT8PetssGS1WhEUFMQFSkKPLRKKVqtFbW0tQkNDkZKS4lFBOpt1Z98zfi0n+76N9TPX39+P2tpaREREiGJmrNj19PSgrq5u1CUY/J+1oUse+D9rnvQ55evs7ERDQwNSUlIQFRUl6EWlwWDAzp07UVlZiUOHDkGhUAj2WISMAwWzRLxsNhuuXLnCZW+rq6sBwKE+Sy6XjzpLwL9Fnp6eLvgKWn6HMHurm+3qdodRUxaLBfX19RgYGIBcLp80w+lHmnrBv9UdFhY2YiaMrbs2Go1QKBQ0j/gOzGYz1Go1bDYb5HL5uC4qh27EYhcGDF3M4c4XFmazGSqVChKJBHK5XPBsdGlpKdavX49f/epXWL16tVu/dsTjUTBL3Af7hVVVVYXy8nKUlZVBrVYjPDycK0/Iz8/H9OnTHQJEq9WKCxcuwGw2u/wWOT8TyNbf+vr6OnTiS6VSlwa4/JW9SUlJiImJEW3A7Swj3epmG8xCQkIwODiI69ev0/ioUeCXrKSmpiIqKkqQx7Hb7cPqpt1xMQd/akhaWhoiIyMFfbzBwUH87ne/Q3V1NQ4dOgS5XC7o4xEyASiYJe6NYRh0dXVxzWXl5eW4ceMGkpOTkZeXB19fXxw5cgRPPvkkNm7cKMpaL7PZPGw8WEBAABfgOrP+VqPRQK1WIywsDCkpKaJ8vcSAXffa2dmJa9euAQB8fX0RHBzs9mUlQhocHIRKpeIWazi7FGCkcVMSicShMXA82wInmtFohEqlgq+vL2QymeCv19mzZ/Hiiy9i+fLlKCgooM8vcRcUzBLPY7fbcfr0aWzcuBH9/f2IjY2FTqfDrFmzuPKEWbNmibZphA2U+PW3bCc+P1CayC9c9ha5wWCAXC6nrTl3wG9YYqc6jFRWAmDYsgCxBErOxDbEdXR0QC6XC17iMxb8aSXskgcvLy+HkSXmIwAAIABJREFU8gRnlwMxDIO2tja0tLQ4pYFwYGAAO3bswKVLl3Do0CGkp6cL+niETDAKZolnYcfHnDp1Cq+99hp++tOfAri5cvH8+fMoKytDRUUFLl26hICAAOTk5HABblJSkmgDDX4nvkaj4bYq8es4hw6dHw2GYdDa2orW1lanNJR4ArYBZ8aMGXdsWBopULrTsgBPo9FoHBrixPozxsdunmMvJodunrubxsDRMhgMUCqVCAwMRFpamqB3RxiGwffff48NGzbg17/+NVatWkXZWOKOKJj1ZHa7He+++y5++9vf4uuvv8Y999zD/X/Hjh1DdXU1vL29kZqaimeffdaFJ504ZrMZx44dw/Lly2/7JcAwDPr7+7na24qKCjQ3NyMuLs5h+PfUqVNFG2gM/cIdGBiAn5/fsPrbW+nv74darcaUKVOQnJxMJQV3YDAYUFtbCx8fH6Snp9/1OCR2WQA/UPLz83OYoOAJs1StVisaGhqg0+mQkZGBoKAgVx9pXPiNgUPft4mod2cvLK9fvw65XI4pU6ZM8DNwNDAwgFdeeQUqlQoHDx5EWlqaoI9HiIAomPVk1dXVkEgkePzxx/Hpp59ywWxrayt+9rOfcf9/fn4+/va3v036W0vsrdDS0lKUl5ejoqICWq0WCoWCW+6QmZmJgIAAVx/1loZuwuI3KrGBkt1uR11dHUwmE+RyudsHGULjz4yVyWSYOnXqhD8G+74NrZvmB0ruNGqKneE8UatVxYr/vmm1Wm7eND+DO5qLnoGBASiVSoSGhiI1NVXQ7CjDMPjuu++wceNGPPPMM3j++efdIltOyG1QMDsZJCUlOQSzhw8fxg8//IDDhw8DAAoLC5GWlobCwkJXHlOULBYLLl++zM2+vXDhAry8vJCdnY2cnBzk5+cjPT1dtLfm+COL+vv70d3dDbPZjLCwMERHR3ObsOjLbGR9fX1Qq9WIjIx06i1ydpYqe1Gi1WphsVgc5haLcdSUyWRCbW0tAEAul0+6jWf81crshQl/tfLQhk6GYXD16lV0dHRAoVAgLCxM0PPp9Xps27YNdXV1OHToEFJSUgR9PL7a2locP34cAQEBOH36NF555RXMnTvXaY9PPNqog1m6/yhSjzzyCDo6Oob98x07duCxxx4b8d/p7Ox0mBkaGhqKzs5Owc7oznx9fTFnzhzMmTMHzz33HBiGgV6vR1VVFUpLS7Fz507U1dUhIiKCy97m5eWJZjyTRCJBUFAQt+t++vTpSEhIgMFggEajQUtLC3Q6nUMdZ1hYmGD1gO7CbDajrq4OZrMZs2fPdvrMWIlEgoCAAAQEBCAmJgbAzcCHbTBrb29HXV0dGIYZtqLXFRcmbMPStWvXnDI+SqwkEgn8/f3h7+/PjRzjN3T29PSgqakJVqsVfn5+GBgYQHh4OLKzswVtSGUYBmfOnMGmTZvw7LPPoqSkxKmfE5vNhrVr1+KTTz6Bl5fXHcvACBEKfepE6vPPPx/zvxMVFYX6+nru91qtluqlRoldevDjH/8YP/7xjwH8c25meXk5SktLcfDgQXR1dSEtLY2bf5udne2SBQkmkwlqtRpWq9UhKPP19UVoaCj356xWK5dJ6uzsxODgILcogM0EToYsGz8oE1tDHDtCKjg4GNOnTwdwswSCbTC7du3asE78u20MHIuBgQGoVCoEBQUhPz+fgpQhJBIJAgMDERgYiJiYGNjtdjQ1NaGzsxNxcXEwm824cOECN7GEPwN3IjLvOp0Ov/3tb9Hc3IyPP/4YSUlJ439SY1RRUQGGYbBv3z4MDg5i2rRpeOaZZ5x+DkKozMCNDS0zoJpZ4dlsNtTW1nLzb6urq2GxWJCVlcVlcDMyMgT74ufXeaampt5Vpoy/KIC9XcpuVAoLC0NISIhHBS46nQ4qlYqrW3TX58ZemLC/hi7mYBvMxhvg2u12NDc3o6uryym3yD2BVquFSqVCZGQkEhMTHbKjQ0e76fX6cWXeGYbB6dOnsXnzZqxcuRLPPPOMy8qJ3nvvPTz33HNobm5GWFgYfvWrX+GnP/0pVqxY4ZLzEI9DNbOerK+vDyUlJXjzzTfxb//2b/jXf/1XzJ8/H8DNaQaVlZXw9vaGTCbzmGkGYjY4OIjq6mpueoJSqURISIjD9rK4uLhxf+H09vZCrVYjKioKiYmJE1ZXydbf8us42Y1KYWFhbjtH1Wq1orGxERqNBgqFwiPX9rJlJux7x29UYoPcsdzm7u/vR21tLfcZc7f33NnsdjsaGxvR19eHjIyMUc9x5mfe2dFu7N0h/gzcoa+/VqvF1q1b0dLSgkOHDiExMVGIpzVqp06dwo4dO3D27FkAwIEDB1BaWoq//OUvLj0X8RgUzBLiKgzDoKenhytPqKioQGtrKxISEhzGg4WFhY0qi2Y0GqFWq8EwDGQymVOmLrBftmyQxJ+jyga4E5EFFAK7Pa6hoQHx8fEe3XU/FNtgxs+8sw1m/Ealodlpq9WK+vp6DAwMICMjw+m1xO5Io9FApVIhJiYGCQkJ4/6M8WcXsyuxT5w4gd7eXuTm5iIwMBDvvPMOCgsL8etf/1oUFxq9vb2YP38+lEolvL29sXnzZoSEhGDLli2uPhrxDBTMEiImbAaHLU+orKyEwWDAzJkzuQzu7NmzHepXjUYjzpw5g5CQEKSlpSEiIsKFz8BxHqdGo4HBYBhXFlAIBoPBYU2oq88jBrfKvLOb52w2G9ra2pCUlITY2NhJE/jfLZvN5jBnV8jAv7u7G9988w2OHz8OtVqNwMBAREVFcXd82KUwrnzPPvroI3z99deIjIzEtWvXsG/fPlGPOSRuhYJZQsTObDbj4sWLXIB76dIlSKVSrqns448/xtNPP40NGzaIIgszFDuuiA2S+FlANns7Uc0ud2K327lRSELNjPUkdrsdPT09aGhogNVqhbe3N7y9vbnSElesenUHbKlPXFzcHbfEjRfDMPjqq6+wdetWrFmzBitWrICXlxe6u7tRVVWFiooKVFZWYvv27cjKyhLsHIS4EAWzhLgbhmFQU1ODVatWQavVIjExEU1NTYiNjeWyt3l5eYiIiBBtkMEfM6XRaKDT6cAwjEOQFBwcPKHnZ2fGUp3n6DAMg+vXr6O1tdUh42+z2Rwy70NXvYq5tERoVqsVdXV1MBgMyMjIEDzz2N/fj5deegmdnZ04ePAgZsyYIejjOZvRaERBQQGOHTuGv/zlL/jFL34BlUqF5cuX49///d+xatUqVx+RiAMFs8R9ffnllzhx4gQ3Pmnbtm2uPpLg7HY7ioqK8Pe//x2vv/46HnroIQA3A4+WlhaUlZVx28t6e3shk8m44HbOnDminh87Ui2gt7c3l7292y58s9kMtVoNi8UChUJBtzZHQa/XO0x2uFPWnG0wY38ZDAZIpVKHCQqePtqtp6cHarUaiYmJgpdhMAyD//3f/8W2bduwdu1aLF++3KMvzhYtWoRFixZh/fr1UCqVOHXqFNauXevqYxHxoGCWuKfBwUFkZmbi8uXLkEqlWLp0KVauXImHH37Y1UcTFMMw+PDDD7FkyZI7rje1Wq24cuUKF+CeP38eAJCVlcUFuHK5XHRbpPj4QZJGo+G68PkB7q1eBzaz2NLSIrqZsWLFzkDt6emBQqFwmEU8FvxNWGx5CX8TFlta4k4rem/FYrE4XCz5+/sL+nh9fX3YvHkz+vv78c477yAuLk7QxxODpqYmzJ07F2fOnMG+ffvw1ltvue3oPCIICmaJe/rqq69QVFSEr776CgCwZ88etLa2Ys+ePS4+mXixt/arqqpQXl6O8vJy1NbWYurUqQ7jwcTc3MPvwmeDJKvV6rDmNSQkBIODg1CpVAgLC0NKSgp98Y1CX18famtrua77ic708Vcrs7+EWhTgLJ2dnWhoaEBycrLgW/8YhsFnn32G7du348UXX8Qvf/lLj87GDrV371689tpr+Mc//oHc3FxXH4eIC62zJe6JVvKOHbtB6sEHH8SDDz4I4OYXZGdnJ9dc9qc//Qnt7e1ISUnhljtkZ2cjJCREFAEuf81rdHQ0AMdh89evX0d3dzdsNhsiIiIQHBwMo9FITUq3YbFYUFdXB6PRiKysLMHKMNjVykFBQYiNjQXwz/dOo9Ggra0NOp0OAIY1mIktaDObzaitrQXDMMjNzRV8GkZvby82bdoEvV6Pzz//nHv9JpPHH38cv/vd7yiQJeNCwSwRlaioKO6LD7g5JJzdhU5GTyKRIDo6Go899hgee+wxADcDjLq6OpSWluLTTz/Fjh07YDKZcM8993AB7qxZs0Rzi9jLywvBwcFc1i81NRUxMTHQ6/XQaDRobGwctgUrLCwMUql0Uge47IVMY2MjkpKSEBMT4/TXw8vLCyEhIQ4Xpvza6ebmZq52mt9g5qrab4Zh0NHRgaamJqSmpgr+dw7DMPjHP/6BHTt2YNOmTXj66adFF9gT4k6ozICIymStmXUVk8mE8+fPc8sdLl++jMDAQOTk5HD1t66aEMDOjPXz80N6evots2Rms9lhPJjJZEJAQIBDk5JYAnShGY1Gbs7u7V4zsRhpdrFUKnVY8CB0rarJZIJKpYKPjw9kMpngn5Xe3l68+OKLMJlM2L9/P2JiYgR9PDEzmUx46aWX8M4776C4uBgrV6509ZGIuFDNLHFfX3zxBT744ANERkbC19d3UkwzEAuGYdDX14fy8nJuPe/Vq1cxY8YMh+1lU6ZMESyDxs6M7ezshEwmw5QpU8b8HAwGg0P9Lb+Gk21S8qRMGDv1oq2tze3n7PJnF2u1WsEuThiGwY0bN3D16lWkp6cLvpSEYRh8+umn2LlzJzZv3oynnnpqUt9BIGQUKJglhEwMNrgsLS1FeXk5KisrodPpoFAouPKEzMzMCcmgsUPpo6OjJzQjzK/h1Gg00Ov1kEgkDre4AwMD3TK40Ol0UKlUCA8PR0pKils1Wo3GrS5O2BW9d7Ocg836+/v7Iz09XfBGwu7ubrz44ouw2WwoKSnh6sIJIbdFwSwhRDgWiwWXLl3iAtyLFy/Cx8cH2dnZyMnJQX5+PtLS0kYdYLhiZqzVaoVOp+MCpIGBAfj5+Q2rvxUrm82GxsZG9Pf3Q6FQONSnejp+cyB7ccIu52AvUIKDg4ddDPEXRjgjg80wDP7nf/4HRUVF2Lp1K5YtW+bUCyaDwYB58+Zh0aJF2L17t9Mel5AJQsEsIcR5GIaBTqdDVVUVV39bX1+PqKgorv42Pz9/2ExYm82G8+fPw2w2O6Xx5k6GzlA1mUwOM1RDQ0NFMQ6MzWBPnz4d8fHxbplRnmg2m41rDtRqtdDr9Q4rev38/NDU1ISQkJAxXWjdra6uLqxfvx5eXl7Yt2+fSz7b69atQ3d3NyIjIymYJe6IgllCiGsxDIO2tjaUl5dzAW53dzfS09ORm5uL0NBQHDx4EI8++ii2bt0qiiBxKP4MVTZIstvtXAYwLCxsxAygUMxmM+rq6mA2m5GRkSF4c5S7YxvMrl27hv7+fvj6+iIgIMChvGSip18wDIOPP/4Yu3btwssvv4x/+Zd/ccnFxtGjRxEUFISLFy9Cr9dTMEvcEc2ZJYS4lkQiQVxcHJ544gk88cQTAG5mz6qqqrB161YolUqkpKTg66+/Rnd3N7fgISMjQzSB7a1mqLIZwJaWFuh0Onh5eXHBkRAjphiGQXt7O5qbm2nr2RiYzWY0NjZiypQpyMzMhLe3N5d9Z+cXm0wmbvscG+Te7RSIzs5OrFu3Dn5+fvj6668RGRk5wc9odK5cuQKlUomioiJcvHjRJWcgxJkoM0uIE7S3t2Pr1q24cOECKioqANwco7R+/XrExcWhrq4OmzZtgkwmc/FJhcOu7H311VexevVqrFixAl5eXhgcHMS5c+e4CQrshi82uM3Ly0NcXJyopw9YrVaH7O3g4CA3YooNku62/pZtVpJKpUhPT580Y8bGgz8RIyMj47bre9ntc/wJChaLxaHBLDQ09LZlCexnu7i4GK+88gqefPJJl15s7Ny5EzabDX5+fvjyyy9hNpvx5JNPYs2aNS47EyF3gcoMCBGTDz74AFKpFNu3b0dlZSUAYNeuXfDy8sKGDRtQU1ODlStX4syZMy4+qXAYhsEbb7yB3/zmN5g2bdpt/1x3d7dDecL169eRmJjoMB4sNDRU1NlJdj0vG+SazeZhHfi3y0Db7Xa0tLTgxo0bkMvlYx5RNlnpdDoolUpEREQgKSnpri6C2BXR7Hun0+kcyktaW1uRnZ0Nf39/dHR0YO3atQgKCsLevXsFH/E1Vq+88gqVGRB3RcEsIWLz7bffYv369Vwwu2DBAhQVFWHBggUAwH1J3i6LNFnZ7XY0NDRw63mrqqpgMBgwc+ZMLsCdPXu2qJcEsPW3/AwgGyCx5QnsiletVguVSoVp06YhOTlZ1FlpsbDb7WhqakJvby8yMjIQHBw84f99nU6Hnp4ebN68GWq1GgDQ39+Pp556Cs8++ywUCoWo3qsPP/wQJSUlMJvNWLVqFZ5++mlXH4mQsaBglhCxGRrMyuVyvPfee5gzZw4AYMaMGfj222+RlpbmymO6DbPZjAsXLnAB7qVLl+Dv74/s7GwuwE1JSRFVcDEUGyCxAa5Op4PFYgEAJCQkICoqymUrXt2JRqOBSqVCdHQ0EhISBH/P29vb8cILLyAkJATLli2DWq1GRUUF1Go1pkyZgvvvvx87duwQ9AyETALUAEaI2EVFRUGn03G/12q1Lh9N5U78/PyQn5+P/Px8/Md//AcYhkF/fz8qKytRVlaGrVu3oqmpCdOnT+fqb3NzcxERESGa4NDLy4vLyvb09ECv1yMhIQHBwcHQ6XRQq9Xcilf+/FsxZ6CdiZ21q9FocM899yAoKEjQx7Pb7Xj//ffx+9//Hjt37sTPf/7zYZ+l7u5uLmtLCHEOCmYJcZHFixfj7NmzWLBgAWpqapCVlUUlBuMgkUgwZcoULFy4EAsXLgRw89b+tWvXUFZWhh9++AFvvfUW+vv7IZPJuOxtVlaWS7Of7MIIm82GOXPmcOO22NpLhmG4Fa/9/f24evUq16DEBsJj3YDlCfr6+lBbW8tdrAj9/t24cQNr1qzB1KlTcfr06VsuXIiIiBBd3Swhno7KDAhxgtOnT+PIkSP47LPP8Pzzz2PdunUAgPXr1yM2Nhb19fXYsmWLR08zEAur1YrLly+jrKwMFRUVOH/+PABgzpw5XAZXLpcLHhwyDIMbN27g6tWrY14YMbRBSavVAgBXf8tuwBJLBnoiWa1W1NfXY3BwEBkZGYJvi7Pb7Th+/Dj27duHoqIiLF682CNfV0JEiGpmCSFkNNjAsLKyEuXl5SgvL4darca0adO44DY/Px8xMTETFsQMDg5CqVQiKCgIaWlpEzJX12azQafTcQHuwMAAvL29uextaGgo/P393ToQ6+npQV1dHeLj4zF9+nTBn0tbWxtWr16NqKgo7NmzhyZKEOJcFMwSQsjdYhgGHR0dXHNZeXk5Ojo6kJqaitzcXOTn5yM7O3vM2U/+/FO5XI7w8HABn8XNEgb+eDCj0eiwICAsLMwt5tZaLBbU1dXBZDI5ZfOZ3W7Hf/7nf6KkpAS7du3Co48+6tYXAYS4KQpmCSFkItntdqjVapSWlqK8vBznzp2D2WzG7NmzuQB35syZtwwO+/v7oVarxzX/dLzYBQH88gSr1crV34aGhoqu/rarqwv19fVISkqa0Oz4rVy/fh2FhYWIi4vD7t27Bb/gIITcEgWzhBAiNKPRiOrqaq7+9vLlywgODkZOTg7XYBYSEoKNGzciOjoaW7ZsEbzjfqzsdvuwBQESicSh/jYoKMjpmUm2Mc5ut0Mul9/1BrXRstvtOHbsGPbv34833ngDjzzyCGVjCXEtCmYJIcTZGIZBb28vt5r35MmTaGhoQG5uLubPn8+NB5syZYqoAyW2/laj0XD1t76+vg7lCVKpVLDn0NHRgcbGRqSkpCA6OlqQx+BrbW1FQUEBEhMTUVxcjLCwMMEfkxByRxTMEkKIq7S3t2P16tWQSCTYs2cPjEYjV55QWVkJvV6PjIwMrjxh9uzZgteBjpfZbOZKEzQaDUwmEwICArgANzQ0dNz1tyaTCSqVCt7e3pDJZILP07Xb7fjrX/+KQ4cOobi4GAsXLhT1RQYhkwwFs4QQ52loaMDWrVuRk5OD1tZWTJs2DS+//DJ6e3uxadMmpKSkoK6uDkVFRU7JtLmS1WrFokWLsG7dOixevHjEP2OxWFBTU8MFuDU1NfDx8UF2djYX4KalpYl6exnDMDAYDA71tzabDcHBwVz2NiQkZFTPgWEYtLe3o7m5GWlpaYiMjBT8/NeuXUNBQQFSU1NRXFyMkJAQwR+TEDImFMwSQpynoqICbW1tWLJkCQBg5syZOHr0KN5991089NBDWLZsGT755BO8//77OHr0qItPKzyGYcaU4WMYBlqtFlVVVSgtLUVFRQXq6+sRHR3NjQfLy8tDVFSUqDOHbP0tW56g0+ng5eXFZW7DwsIQGBjo8ByMRiOUSiWkUinS09MFn65gt9vx5z//GX/84x/x5ptv4uGHH3baa3qriz5CyIgomCWEuI5CocDHH3+MhQsX4ocffkB8fDx6e3uRlpaG3t5eVx/PLTAMg+vXr6O8vJwLcHt6epCens7V3mZnZw8LDsXGarVy9bdarRYDAwPw8/NDaGgorFYr+vr6IJfLMW3aNMHPcvXqVRQUFEAul+P1119HcHCw4I/Jd6uLvtzcXKeegxA3QcEsIcQ1PvroI3z77bd46623IJVK0dHRgfDwcFitVvj6+sJisUzIkoDJyGazQalUcrNvq6urYbfbkZmZyWVvFQqF6F9fjUYDpVIJiUQCb29vWCwWBAYGctnb0NDQCX0Odrsdhw8fxp///Gfs2bMHP/nJT0RxAcBe9CkUClcfhRAxomCWEE/3xhtvYNu2bVi6dCmOHTuGEydO4NVXX8ULL7yA5cuXu+RM33zzDT766CPs3bsXXl5eiI+Pp8ysgBiGweDgIM6dO8dNUKitrUV4eDhyc3O5+tu4uDhRBG8Mw6ClpQVtbW1QKBTcDFf2efDrb+12O0JCQrgANzg4+K5qiJuamlBQUIBZs2Zh165dohmNxr/oI4SMaNR/aYn78p0QcksbNmyAVCrFsWPHYLVa0dPTg3feeQfz5893yXlOnjyJM2fO4K233sKNGzdw9epVLF68GGfPnkV8fDy+//77WzZEkbsjkUgQFBSEBQsWYMGCBQBuBoZdXV1cecKRI0fQ1taGpKQkLnubk5OD0NBQpwa4AwMDUCqVCAsLQ35+vsNiBvZ5BAUFITY2FsDNbKper4dGo0FLS4tD/S2bvb1diYXNZsMf//hHHDlyBHv37sUDDzwgioAeuHnR980332Dv3r2uPgohHoEys4S4MYZhsGjRIsTFxSEzMxNr1651yTmqqqrw4IMPIi8vD8DNwGXVqlV47LHHsHHjRiQmJqKhoQG7du3y+GkGYmS321FfX8+t5z137hwMBgNmzZrFBbj33HOPIKOw7HY7rl27ho6ODigUinHNcLVarQ7Z28HBQUilUoSEhKC6uhr33nsv4uPj0djYiIKCAmRmZqKoqEg02Vjgnxd9r732GnfRd++997r6WISIEZUZEDJZ1NTUIDMzE2fPnnVZVpa4H5PJhAsXLnD1t5cuXYK/v7/D9rLk5ORxjQfT6/VQKpWYOnXquP9bt2I0GtHd3Y3i4mJUV1eju7sber0ey5Ytw1NPPYWcnBynN3rdyq0u+lasWOHagxEiThTMEjJZFBQUIDY2Fn/9619RXV2NwMBAVx+JuCGGYdDf34+KigouwG1ubsb06dO52tvc3FxMmzbtjrfr7XY7mpqa0NPTg4yMDKfMcK2vr0dBQQFycnKwfPlyXLp0CWVlZaiqqoLFYkFubi4OHDggmlIDQsgdUTBLyGRw5MgRREdH45FHHsHSpUsRHR2N/fv3u/pYxEOwJQJscFtRUQGNRgO5XM4FuFlZWfD39+eCxDNnzqCvrw+zZ89GYmKi4IsfbDYbDhw4gOPHj+Ptt9/G/fffP+zPmEwm1NbWIjMzU9CzEEImFAWzhHi64uJi/Nd//Rf27duH++67D6+//jo2b96MtWvX4tVXX0VAQICrj0g8kNVq5bKeFRUVOH/+PCQSCWbPno2uri40Nzfj3XffdUrgqFarUVhYiLlz59JnnhDPQ8EsIYQQ4TEMg6+++gqrVq3CzJkz4e3tDbVajYiICG57WX5+PqKjoyfsFr/VasX+/fvx3//939zFHCHE49BoLkIImWh2ux0///nPMW/ePJjNZjQ0NOBPf/oTDAYDNm3ahJSUFNTV1aGoqGhSTG0wGo3YvHkzLl26hFOnTiElJQXAzQC3vb2dm55w6NAhdHZ2Ii0tjQtws7OzERwcPOYAV6VSobCwEPfddx++++47ysYSQigzSwgho2W321FUVIStW7cCAJYsWYJly5bhzJkzeOihh7Bs2TJ88skneP/993H06FEXn1Z4FosFH374IX7xi1/cMSi12WxQq9UoLS1FeXk5zp07B4vFgszMTK7+NiMjA76+viP++1arFX/4wx9w4sQJlJSUYN68eUI8JUKIeFCZASGECMlqtWLevHk4ePAgnnjiCdp0dhcMBgOqq6u5+tsrV64gODiYy97m5eUhPj4etbW1KCwsxAMPPIBt27bB39/f1UcnhAiPgllCCBHK559/jt///veYN28etm/fDqlUio6ODoSHh8NqtcLX1xcWiwU+PlTJNRYMw6Cnp4dbzVtRUYHa2lrY7Xa89957mDt3rquPSAhxHgpmCSFEaMuXL8f8+fPx2muvUWZWIGazGUajEaGhoa4+CiHEuUYdzAo7AJAQQjzIlStXcPLkSe73ycnJaGxsxOLFi3H27FkAwPfff4/Fixe76ogex8/PjwKkxqYqAAAC+ElEQVRZQsht0T0wQggZJalUisOHD6O6uhoWiwVKpRJvv/02/Pz8sHHjRqjVajQ0NGD37t2uPiohhEwaVGZACCFkUvvyyy9x4sQJREVFQSKRYNu2ba4+EiGEamYJIYSQOxscHERmZiYuX74MqVSKpUuXYuXKlXj44YddfTRCJjuqmSWEEELu5OzZs0hMTIRUKgUA/OhHP3KoiyaEiB8Fs4QQQiatzs5OhISEcL8PDQ1FZ2enC09ECBkrCmYJIYRMWlFRUdDpdNzvtVotoqKiXHgiQshYUTBLCCFk0rr33ntx9epVmEwmADRajRB3RA1ghBBCbslgMGDevHlYtGgRdu/eDaPRiPXr1yMuLg51dXXYtGkTZDKZq485Ll988QU++OADREZGwtfXl6YZECIONM2AEELI+K1btw7d3d2IjIzE7t27sWvXLnh5eWHDhg2oqanBypUrcebMGVcfkxDieWiaASGEkPE5evQofvSjHyE5OZn7ZydPnsS9994LAJg9ezYuXLgArVbrqiMSQggFs4QQQoa7cuUKlEolnnzySYd/Tt3/hBCxoXW2hBBChvnoo4/g7++PXbt24bvvvoPZbMbevXup+58QIjoUzBJCCBnmpZde4v630WiEXq/HmjVrYDQacfbsWSxYsAA1NTXIyspCaGioC09KCJnsqAGMEELILX344YcoKSmB2WzGqlWr8Pjjj2P9+vWIjY1FfX09tmzZ4vbTDAghokTTDAghhBBCiNuiaQaEEEIIIcTzUTBLCCGEEELcFgWzhBBCCCHEbVEwSwghhBBC3BYFs4QQQgghxG1RMEsIIYQQQtwWBbOEEEIIIcRtUTBLCCGEEELcFgWzhBBCCCHEbfmM8c+PehsDIYQQQgghQqPMLCGEEEIIcVsUzBJCCCGEELdFwSwhhBBCCHFbFMwSQgghhBC3RcEsIYQQQghxWxTMEkIIIYQQt0XBLCGEEEIIcVsUzBJCCCGEELdFwSwhhBBCCHFbFMwSQgghhBC39f/eO6OO08ihjQAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 864x576 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Example 9\n",
- "#from mpl_toolkits.mplot3d import axes3d; \n",
- "import matplotlib.pyplot as plt; from matplotlib import cm; import numpy as np \n",
- "Z=np.loadtxt(open(\"data/times_affinity.csv\", \"rt\"), delimiter=\",\", skiprows=1,usecols=(np.arange(1,11)))\n",
- "Z=np.log(Z).T\n",
- "fig = plt.figure(figsize=(12,8)) \n",
- "ax = plt.axes(projection='3d') \n",
- "X=np.arange(0,40,1)\n",
- "Y=np.arange(0,10,1)\n",
- "X, Y = np.meshgrid(X, Y)\n",
- "\n",
- "#cset = ax.contourf(X, Y, Z, zdir='x', offset=-10, alpha=0.5, cmap=cm.coolwarm)\n",
- "#cset = ax.contourf(X, Y, Z, zdir='y', offset=14, alpha=0.5, cmap=cm.coolwarm)\n",
- "#cset = ax.contourf(X, Y, Z, zdir='z', offset=0 , alpha=0.5, cmap=cm.coolwarm) \n",
- "surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)\n",
- "#fig.colorbar(surf, drawedges='True',shrink=0.8, aspect=18, orientation='vertical',)\n",
- "#surf = ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1)\n",
- "\n",
- "ax.azim = -60\n",
- "ax.elev = 30\n",
- "ax.auto_scale_xyz([-10, 40], [0, 12], [0, 5])\n",
- "ax.set_xlabel('X')\n",
- "ax.set_ylabel('Y')\n",
- "ax.set_zlabel('Z')\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Heatmap - multiplot"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 227,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAGcCAYAAADJWJn5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzs3XucHFWd///Xe4aQG0QJCXJNCBgFMYISUS4KCOvXFf2u4HVVLupvo4hfZXENfF1BWNgVIrILq4JZ2M0KggjoosYfK3IJhIsQXLmqiIaLSkhC0ARDLjPz+f5RNaTT6e6q6eqenup5P3n0g6mqU3XOTPr0p8+lTikiMDMzs/Lp6XQBzMzMrDkO4mZmZiXlIG5mZlZSDuJmZmYl5SBuZmZWUg7iZmZmJeUgbsNO0l9I+rmkkLRI0uSq45J0lqRbJN0q6X5J769zrTPTa91adc1bJT0u6bAWlnuapLslDdt9mZLOkLRM0pnDlWdF3j9q5d/PzFpPvk/cOiENDrcAYyKir+rYVsDDwGsjYq2kw4EfA7tHxO+r0p4J3BoRt1Zfs/JYg3LsDiyNCOUs95DSt4KkBcDjEXHmcOWZ5jsJWBP+kDAbsbbqdAHMaugH3hMRa9Pte0jeq7sAv69KeyXwbJ3rNDpmGSJidafLYGaNuTvdRpxIPAhJ1zrwcWAJ8D810j4aETUD9eAxSWMkfVnSnenry+m+lwDfTvO5NX31SnqTpJvT7TslvStv2SVtI+nfJC1OX5dJmpoeO13SXem1fyhp54rzdpB0jaTb0jT/LGl8xaWnSLpC0kOS/rMqz+PSbv5Fkq5MW9C1yvZdSesknSrp+5J+K+m96fk3S3pQ0sw07ecqu/ElvUzS/58OcSyWdGq6f4Kk76R5L5Z0QUV+e0r6cXrsdkkHVRw7I/09b5F0taSdapR3Tjok8t3097orvc6MijT7p3+zRZJukrRX1bnfTv89fiHp1jp/lw+lf7+b09cR6f6a75uqv+XnJP1A0mpJJ1Sds1jSF9P3sFl7RIRffg37CzgMCGCrBmn+AvgN8BAws9lrAqcDPwF609d/A6enx3ZPqsFm6d8OvDz9eRJJ6/8l9dJXnTsf+Pf05x7g+8Bh6fb/YdMQ1gnA5RXn/Rj4Yvrz1sDPSIYPABaQfIEZC4wj6V04MD12MLASmJpufxm4tEH5HgcuSn9+F7AcODrdvgi4pCLtAuDM9Od5wKnpzxOBxenPnwQuTn/uBe6t+PkXwEfT7dek5dwWeBXwSMXf4p8H/0Y1ynsm8Edgp3T788Cd6c8vAVYAb0m3jwJ+BfRUnLsMmJqW57wa1z9oME26/R5gQdb7puJvOfhvfXia/98DN6fpxwB3Ah/udH3zq3tfbonbiBURN0bEnsApwGJJ05u81HHANyOiPyL6gW8CH2mQ/iHgbEl3kATh7YFXZmUiqSfNa0Fa/gHgsyQBC+Ap4BZJtwEnA/un5+1C8oXlP9LzNgAfJQlQg26JiPURsQ54FBhsjZ4A/CAiBtNeCXwoo/V3Y8XvOZUkUAE8AOxR55xVwF9K2ici/gy8tWL/myS9Mf3bHprufyOwJ3B5+js9QPJl6B3AGmBH4Ji0ZXsqsLhBeRdFxNPpz5cDB0qall7r+Yi4Oc1jYXrdN1Sce1dErEj/7U+tce2PAD+q+Pv9F3Bx+nOe9831ad63pPmfAPxnes5G4Brg2Aa/m1khHhO3ES8ifizpIeBvgC80cYld2Twgrkj31fNN4MGI+GsASY8DE3LkM5WktfxiXhHx6/QaM4HvAAdHxL1KJuEtqCgfVef9vOralePT60la64Pnvqqiq3gr4BmSLx4r65RzTfr/vjSvyu2ta56RtPD/DFwtqQ/4R+CaiPi2komI/yJpe+ACkiC4K0mvyI0V3yfGkvRoPCXpKJLg/TXgWySt3s0mOFZ4ruLnwaGTndI8Jld1k69If/dBf6pzzUG7knx5ASCSSZY/rTiW9b6pvv6uwCmSBoP9NiQ9CWZt4SBuI4aSMepDgF8DO8fms8r/TNKN24ynSALsoKnA7xqkPwA4v2J7TM58VpAE2KkkXcmk494DwGuB1RFxb41rPlVRrifT8/YAnouIygBWy1PAbyPipMEdkqZERL0A3qwdIuJfgX+VdCTwQ0k/IwliV0fEFZJeC/xE0i/Tcm2MiMMqyjURGJA0AXgkIt4laUfguyQB/Yt18q68BXFK+v+n0zx+V5XHJGDdEH6vzd4b6ReSfSLi/upjZL9vBq93TkRck16vB3jpEMpjNiTuTreRZDvgvcDOwOfSD1QkvZxkvPumJq+7APiwkklrPcCHSbuuSVul6QSt0yS9EXiMtEtW0mtIWn2Z0u7zb5J0qQ5+gF+Wnv8YsJ2kV6TJ31Zx3h9IxsQHzxtL0mqv1yqu/t2OkrRdeu4rgR/kKe8QfUnSfunPPwU2AAI+RTIWDPAgSfd6b5rmSUnHpOXaiqSr+hUkX5LOAoiIZSTj2L0N8j6oYuLbcSRd5E8CPwS2l/T6NI+JJLcYvmQIv9cC4O2SBr8cvJ/034HG75tG1/ugpMHf53iScXKz9uj0oLxfo+8FvAlYRNLdeh1wbfr6EcmH4GTgQpJJQYuAnwMnZVzzLWm6SM+ZXHFsDHBeer07SVrZYyqOfwu4j2SseDzJZLFfkASEi0hafT8H3gzcneZxK9BboxzbAJeSjPHeWVlu4GySyVDXA98gaTF+Mz22A8n46W3pee9J959CMvHqceBo4AyS7tlfsmlC14fTct0M3AC8os7f6Jtpnj8nGeMf/F2uJwmsv0yvPQ/4XEW+HyMJ1LeledwHfDq95htJvlzdTHIHwZcq8tszLc8i4HY2TXLbkeRLyiLgDpKW+EvrlPlM4Or0fXFXep09Ko7vn/5bLErL9450/wfTsi8b/Bs3eO98OL32rSTvw0lZ75uqv+UHq95r56Z/21tIxvAndLrO+dW9Ly/2YmYjVnqL2+4RcUKHi2I2Irk73czMrKQcxM1sRJI0h2R8+m2SPK5sVoO7083MzErKLXEzM7OSchA3MzMrKQdxMzOzknIQNzMzKykHcTMzs5JyEDczMyspB3EzM7OSchA3MzMrKQdxMzOzknIQNzMzKykHcTMzs5JyEDczMyspB3EzM7OSchA3MzMrKQdxMzOzknIQNzMzKykHcTMzs5JyEDczMyspB3EzM7OSchA3q0HSjpIulXRvjrQzJF0n6TRJ35b0v4ejjGaWrdvrsoO4WW2HANcDypF2LrA4Is4FzgO+0s6CmdmQdHVddhA3qyEirgXWVO6TtI+kb0r6nKTLJO2RHnoGmJr+PBW4bxiLamYNdHtd3qrTBTArkUuBz0bEnZIOI/mWfjRwAfA9SRcABwBnd66IZpZD19RlB3Gz/F4DvFXSm4HxwPPp/gXApRFxlaSpwK8l7RERqzpUTjNrrGvqsoO4WX73A9+NiAckjSX55g6wG/B0+vNzwAAeqjIbybqmLisiOl0GsxFH0qHAccDbgItJutt2Bz4LLCWp7FdExGJJhwAnAz8DZgD3RcQlnSi3mW2u2+uyg7iZmVlJjehuAjMzM6vPQdzMzKykumZi29YaG+OY2OliWElMn7Wm4fHf/66fVasGMheH+F+HT4xnV/XXPHbfA+v/OyLe1uh8STsC5wD7RsTraxw/AXgj8BvgdcC/RsSdWeUqM0ke47Pc9tt3h4bHn3xqNc8++0J2XX7ba+LZlc/XPX7ffUsb1udO1eWuCeLjmMgbdESni2ElccnCxQ2Pv+uolbmus3JVH3fesEvNY+N2XjolxyUGV5Par87xXYCTI2KdpDeQ3N86K1fhSq230wWwklh08wcbHj/0LVfmus7Klau566dn1D0+dquPZdXnjtTltgTxWt9I0m8hnwDWpckui4jLa5x7JHAMsByIiDirHWU0a4UA+qjdEs91fsS16WIT9Y7/Y8VmD5vuZx02rs82GkQE/QPri5zfkbrcrpZ4vW8kH4iIx+udJGkCcAmwT0SsTxeiPyIibmpTOc0KCYL++nd4TJG0pGJ7fkTMbyYfSQI+A5zSzPkFuT7bKBBE9DVK0JL63Oq63JYg3uAbyackLQMmAF+tsQrOgcATETH4degO4CigZqWXNAeYAzCOCa0outmQBLCRgXqHV0bE7KJ5pJX+y8CCiLir6PWGajjqc2VdNuuIGGCgf12jFIXrczvq8nDOTl8EnBcR5wNLgGtqpNmBzReqX53uqyki5kfE7IiYPYaxLS2sWR4BbIyBmq9mSZqYLvmIpF7gQuAHEXGDpHe3puSFtbQ+V9bllpfULJcgBtbVfTVjOOrysE1si4ilFZs3A9+X1BsRlQOKy4FtK7YnpfvMRqzmw/WLq0kdC+wk6Qskq0mdQDLh5RMk39rfBbwm+RLPnsB1RcrbCq7P1n0CBjY2fXan6vKwBXFJXwJOj2TQYSawdLDCS5qRfijcBUyXNDbtgjsY+PpwldFsqCKCDQVWPYyIRSSt2kpfqzh+Cp0ZB2/I9dm6TcQA0bg7PeP8ztTlds1Or/WNZBlwsaSlJN9Mjk3TTgUWS9ozItZKOhG4SNIK4AFPgrGh+PU3X5cr3Rg1vsUs86bSVCA25k5dTq7P1gmPvP2QfAl7xzc+rpyjxhFQIIh3SrsmttX6RnJhnbQrSO6fG9y+EbixHeUya7VkTLy7g7jrs40GigHU5yBuNqoE0N/lLXGz0SFgoOEtZiOSg7hZAUlL3I8gMCu9CNTf/GIvneIgblZAIDaGlwg1K78B1OcgbjaqBGKDg7hZ+UU4iJuNNgEM+Im+ZuUXAQPNPwehUxzEzQqIcEvcrDsE6tvQ6UIMmYO4WQHJ2ukO4mZlp3AQNxuFRL9np5uVXwRyd7pZ+yz724My0zz0ln/Jda0/ZSx4nn/FNjw73WyIztsj+4F1u//Xq3Nda+O6ZY0TaAjrL/Y1v3Z6pziImxWQ3GLmamRWehHg7nSz0WXAt5iZdYcI1O+WuNmo41vMzLrEQJEHC3eGg7hZARFesc2sK4THxM1GnQA2eEzcrPwioM8PQDEbVYqunS5pR+AcYN+IeH2N4z3APwHPA9OByyLi7qYzNLPaIqBAS7xTdbktQbzWLyPpVGBHYBmwP3BGRPyyxrl3A4MPde2PiCPaUUazVghgoNh94ocA1wP71Tn+PmBSRJwmaTJwt6S9I2LYbmh1fbbRQAQqNibekbrcrhk5g79M5Q162wCnRMR5wHXAl+uce0NEHJa+XOFtRBtsidd65To/4lpgTYMkRwF3pWlXkQTEfYqWe4hcn637BUl3er1X1ukdqsttaYlHxLWSDqvad3rFZg9Jl0Its9Jv+eOBeyNiYb18JM0B5gCMY0KhMltnLf9U9kIu93/u65lpVua8ReSp/rENj2/I+f02Y2LbFElLKrbnR8T8XBfeZAc2/2BYne4bNsNRnyvrspXbWdM/kZnms48dmJlm7doncuXXs/Lhhse18YVc10m60xs2iovW57bU5WEfE5e0NXA8cFKdJOdFxD2SeoHbJK2JiNtqJUz/gPMBJmlytKXAZhkaLLu6MiJmF7z8cmDbiu1J6b4RoVX1ubIuS3Jdts5o3J1etD63pS4P6w2uaYW/GPj7iPhNrTQRcU/6/37gduDw4Suh2dAU7U6vRdJESVPTzYXAgen+ycA4oHHTY5i4PltXGWyJ13s1YTjq8rAFcUnjgW8AF0TEfZLeXXFsRvr/vSR9rOK0mcBjw1VGs6EaXDu92SAu6VDgWGAnSV9I68kJwNlpku8AayR9kWTc+bjhnNRWj+uzdZ+A/v76rwydqsvtmp2+2S8DfAX4FvBqYIaSBeknAtel31IWS9qTZIzgHZJ2JulqeAq4qh1lNGuFQPQVaHVHxCJgUdXur1UcHwBObTqDFnB9tlEhgL7mZ6d3qi63a2JbrV/mmDppVwC7pJt/AI5uR5nM2iEC+iPvU5LKyfXZRoMIiPKtuurFXsyKCETfgJddNSu9APrKN6fSQdysgGRM3A9AMesKHZ9tMnQO4maFFBsTN7MRIiD6yjc05iBubfXkGdmLuABc/dELMtM8ujH7a/LLevO1ih/fOKXh8fWxItd1RsOYuBnAglcdnyvdMT9enZnmzysWZ6bpnTQzV35jnql5d+OL1Lc+13UAGChfXXYQNyvAY+JmXSJE9JVvaMxB3KyAZC5M+Sq+mVUJiP7y1WUHcbOCCj7FzMxGioHy1WUHcbMCIuSWuFk3CLklbjbaJIs8la/im9nmIiD6yje/xUHcrIBkYpuDuFn5uSVuNioNUL7bUsysSuAxcbPRJsLd6WbdQQy4JW42urg73axLeEzcRpuBm3bLTHP1ntkrsQF8f/V+mWnese39mWnW9/Tlyu8VY5Y3PD5OG3NdB6Dfs9Ot5FZ/7mXZiT6Tr06Mv/P6zDTr3nhUZpqBvudz5bdhl1c1PB5jnsp1nQgR/Q7iZqNKBAx42VWzrhBedjUhaUfgHGDfiHh9um8ccD7we2AmcG5EPFrj3CNJnlW8HIiIOKsdZTRrDdFfoDs96/0uaQZJvbkX2A+4MiK+33x5myqj67N1vxa0xDtRn4ccxCVNi4gnM5IdAlxPUshBJwNPRsQ8SbOAy4A3VV17AnAJsE9ErJd0naQjIuKmoZbTbDgENB3Ec77f5wKLI+KfJb0W+A4wrEEc12cbBQIKTWzrVH0eUoklTQduzUoXEdcCa6p2HwXclR5/ENhX0qSqNAcCT0TE4GNn7kjPMxuZIl0kosYrhzzv92eAqenPU4H7WlHsoXB9tlEhku70eq8cOlKfh9QSj4gnJO3ZZF47sPkHwep03+ocaWqSNAeYAzCOCU0Wy6x5QcOJbVMkLanYnh8R8yu287zfLwC+J+kC4ADg7GIlbpmW1ufKumzWGZnd6SOyPjczJv4B4KomzlsObFuxPSndN9Q0L0r/gPMBJmlyvraPWUuJ/vrf0ldGxOwGJ+d5vy8ALo2IqyRNBX4taY+IWNVsiVukpfW5si5Lcl224ReZ3ekjsj7XLbGkpZJ+W/VaCny1ybwWknQ3kI6h3R8Rq9PtGWmau4Dpksam2wen55mNSBEwMNBT85VDzfe7pMkVXdO7AU+nPz8HDDDEYbA2cX22rhKIgf7euq8cOlKfG7XE50XExZL+BrgZ+C2wJ8nMu4YkHQocC+wk6QvAV4ALgfPT7ZcDH0vTTgUWS9ozItZKOhG4SNIK4AFPgrGRrtlbzOq93yXNA1YB5wJ/C5ws6SBgBvD5iFjZoqLn4vpso0Ik94o3fXqH6nPdIB4RF6c/7hwRv0l/fkzSS3L8MouARTUOnVQj7Qpgl4rtG4Ebs/Kw9vrddftkpulbmf3t9Nxxf5krv+NedmdmmuX922Sm2XWrP+bKrz9jvfMYwnroAwXuLa31fo+IuRU/LwYWN51BC7g+l9vvPviazDTPLh2TmWanK76XK7++v8xeuKn3T3/Ivs7kV+fKj4H+jAT5R2eKLrvaifqcZ0z8dZLeC/waeAWwbysLYFZmgbzYi1kXiFDebvMRJU8Q/wwwD9gHeBj4dFtLZFYmUc5VnsxsSznnsowodYO4pG0i4vmIeBx4X8X+icNRMLOyKDKOZmYjROS+H3xEadQSP1fS12vsn0OyWpPZqBcUGxM3s5Ehqcvd1Z3+IeDtsMUMn0k4iJsl3J1u1h1C9HfZ88TnRsS/Ve+U9JE2lsesfLw0iVnpBeUcGmt0i9kWATzd/x/tK45Z2ZRzHM3MttRVE9vMLAd3p5t1hQjR36W3mFkXWXHigbnSbVj/Qmaaz732x5lp7vpTs8/L2dKrtn4uM821a16Z61p7bF13SX6g4UNNtlTCLjgrv9N3OzFXunVrsx+UNe2kZZlp4sG+XPnlGV3auNtBmWkm3PGNXPlt3HlG4wT9G3NdB8rZEh9yiSXtkp3KbBSJOi8zK49IllCu9xqpGt0nflydQ+8E3tue4piVjLvTzbpCoFK2xBt1px8P3Aa8CthA8gCUPYDxw1Aus/JwEDfrCv1dFsQ/HREPS/q7iDh/cKek04ehXGblEKCBThfCzIqKUHcF8Yh4OP2x+lEye7WvOGZlI09sM+sSXXWfeIVfSHoIeAyYCVzR3iKZlYxb4malF3RfdzoAEXGepIXA3sAvIuKhIhlK2h24CXgq3TWJ5OHpJ1SkOQH4BLAu3XVZRFxeJF+ztghG7Zi467J1lW7rTq+UBu6HIKmUEbGgQJ5rgI9HxE/S651F1UPUUx9In6BmNqJp9N5O5rpsXSO5M7R8X8gzg7ikDwJfBKYALwATgAXNZhgRzwKDlX4sMDsivlgj6ackLUvz+2pErGo2T7O2KhDEJR0JHAMsByIizqo6LuD/pJu7Ay+NiI82n2PruC5btynaEu9Efc7TEj+IpCv9c2nX+twiGVb5IHBVjf2LgIURsULS24FrgCOqE0maQ/JoVMYxoYXFKqeVH89ejW3tjvm+afavHJt9rYGtM9PMnNB4ZbRBE3rWZ6Z5oi/73/iN43+bM7/Gq09trf5c1wFQk93pkiYAlwD7RMR6SddJOiIibqpI9mHgjxHxzfSc1zSVWfu1rC4bfH7XT2ameeVL1uS61lPP7JiZZvq6pZlpNG1crvz6xm2TmaZ3xQOZadbtfXCu/AbGvqTh8RjzSK7rFJ2d3qn6nKfEv4uIAWDwX7CVK7a9F7i6emdELI2IFenmzcChkrZY1DYi5kfE7IiYPYbsoGPWckEysa3WC6ZIWlLxqg5SBwJPRMTgN5g7gKOq0nwImCzp05L+CXi+Pb9IYS2ry20up1ld/dFT98UIrc95WuIHSHonsF7STWz5fPGmSDocuDMiNqbbk4G+iFgt6UvA6RHRRzIjfmlE5G8amQ2jBmPiKzOC0g4k48qDVqf7Kk0HJkXEP0h6BXCDpL1HUn1wXbZukONRpCOyPueZnX4MgKQfAY8AdzWbWZU5bBobADgNWAWcCywDLpa0FJgFHNuiPM1ar/lbzJYD21ZsT0r3VVoN/BQgIh6VNAnYDXi86Vxbz3XZukDh2ekdqc+5ZqenLfFJwM+BPzebWaWI+Ouq7bkVP1/YijzM2k3R/Jg4yRfi6ZLGpl1wBwNfr2zJktzCtQdAWuF7SQLjiOG6bN0gAvqLLfbSkfqcZ3b6PGAqyfrpj5B8u/50kUzNukmzy65GxFpJJwIXSVpBco/1TWmdG2zJngfMk/R5YE/g+IhYV/+qZtasIT2CuEqn6nOelvgfI2KupFMj4n8k/VWRDM26ToFbzCLiRqrura5qyf4J+HjzOZhZHkHxR452oj7nCeJTBvNP/79tvYRmo44fgGLWNQp2p3dEniD+qKRHgAFJ7wG+0eYymZWKg7hZ+UVAfwmXUM4TxK8EFpM8vezBiPhVe4tktfzx2OyFXLZek92v+3zOIZ+e7TdkprnwriMz07zl1b/Mld/rJjyemebN47IXt/jTwMZc+WWl6inSR27WwCdfdlJmmhXZax/Rm3O9312mZi+49NCF2WuOvOodt+XKr2dm9q3PsfdfZ6bZuC7nfK++FxofV/5x7oFuXHYVeBQ4MiKubXdhzErH3elmXSGK32LWEXlKfEXlk8skva6N5TErn/ortplZSQTJmHi910iVpyX+UknnAr8g+T3fSbLEotmoJ9wSN+sWIzlY15OnJb4/ydPLdgdmAJPbWSCzUol0wZcaLzMrjwgYCNV9jVR5WuInRsTdgxuSZraxPGbl45a4WVfoypZ4RNwtaTtJ0yRNI3kKi5mlNFD7ZWblEdQfDx/JwT3PsquXAQcAK0iGAKcBZ7a3WGYl4dnpZl1hcGJb2eTpTp8YEbMGNyQd1r7imJWQx7/NusJACetyniB+r6QJEbE23d6unQUajeKgfTPT9G7Ifndt2Db7W2TfNvnepePHZy/2cs4B12em+e7KfHckbtuTsWADcMu6SZlp3jo+30P2nunPzi8vt8Rt0OvHZz9pdW1f9nWmjsuup1Mm5HuvT9w2O92003OsLrMoXyu1f8JLMtP0PvytzDTjZn0sV37rnn8sI0W+crfgKWYdUTeIp8//DZJHpZ0t6Zn00CTge8NQNrMRzzPRzbpHVwVxYF5EXFy9U1K+r0cNSLobGHz8Wn9EHFF1fBxwPvB7YCZwbkQ8WjRfs7YYxUHcddm6RVDOG00aBfEDJK2NiP+s3BkRl7Ug3xsi4swGx08GnoyIeZJmAZcBb2pBvmYtN8q7012XrWt0W0t8ZXUAb6FZkk4FxgP3RsTCquNHAZ8HiIgHJe0raVJErG5Tecya49nprsvWFQLoL2FdbhTEa3YSSjohIhYUzPe8iLhHUi9wm6Q1EVH5iJwdgMpHVq1O921W8SXNAeYAjGNCwSKZNadIEJd0JHAMsByIiDirTroPAVcA20ZE9mOihk/L67JZR7TgfvBO1OdGQXxO+vzwzfImmdi2oEimEXFP+v9+SbcDhwOVFX85sG3F9qR0X/V15gPzASZp8igembSOavKdJ2kCcAmwT0Ssl3SdpCMi4qaqdHsDrypczjZoR12WPFXQhl/RMfFO1edGK7Z9l+RhJ9WvK4pkKGmvqslxM4HHJE2WNHgP0ULgwDT9LOB+d7/ZiBQNV2ybImlJxau6pXkg8EREDN7fcwdJ9/OL0g+GuUDNb/Sd5Lps3aY/6r8YofU5a0z84eqd6fhXEauBd0jameRb+VPAVcC5wKr0/xcC50v6AvByoPCMeLN2yHiK2cqImN3g9HpdzZX+ETg7IjZII27SjeuydY1kTLxhHRuR9blREH+jpONrzE5fV++EPCLiD8DRNQ7NrUjzAnBSkXxGgo1vbfTvvYn6snsPe3KkIcd4Tmydr6fyz8snZqY57crjMtN867h/yZXfmoFxmWkOH5fdgFvZn71IDcCfBnobHu/PuUAEgJpf5qlhV7Ok3UgWV3pfRYU/RdKPImJJs5m2ymiqy2+dkG+4fmNkd8huyPF+yfOWGj8m33v9qad2yUxzy0emZqb5qx/ukSu/nheey0wT+2Q/gmPd2sdz5ae1Tzc+PrAx13WSZVdzJa2nI/W5bhCPiDc3e1GzUSMocp/4XcB0SWPTLriDga9Lmgz0RcRTwAmDiSV9CbhghE1sM+saBSend6Q+51m6s6llAAAgAElEQVR21cwaaHZ2ekSslXQicJGkFcADEXGTpHls6o5G0lTg4+lpcyV9IyJ+X7zkZjYoolhLvFP12UHcrKAit5hFxI3AjVX75lZtrwDOSV9m1iZF7xPvRH12EDcrwmunm3WFblx21cwyZMxON7MSKTixrSMcxM0KKjA73cxGiIjuW3bVzLIEqL/ThTCzogLIcyfvSOMgblZUCSu+mW2pjFXZQdysiHB3ulm3cHf6KPLCXx2QmaZ3fb4P997+HP2xORYQG7M2O7+xyxuvVDZo4yteyExz5uHXZKZ5tj975TeAgYbL+Cee6MteE+EVY/I9ze6pjL/5wJBWbMud1Eagd0/6ZGaaF/LUUWBtjhXblOO99ccci7H95rnt8xSJA/d8NDPNe7/0RGaa/jX58tNA9t9qw6r/yUwzfuohufJbv3KL1cE3l6M8MNidXr4v5A7iZgUowi1xsy5QdLGXTnEQNyvI94mbdYMgSjgq7iBuVpC7083Kz7PTzUajFjz6yMw6L6nK5avLDuJmBbk73aw7hIN4Y5L2JFn0/WfArsCzEfEPVWlOAD4BDD63/LKIuHw4y2k2FKN1Ypvrs3UTz07PZzLw7Yi4HkDSI5IWRsR9Vek+EBGPD3PZzIZMo/s+cddn6yr9ntjWWETcW7WrB/hzjaSfkrQMmAB8NSJWtb1wZk3SKB0Td322bhIR9OW4z3+k6diYuKSjgf+OiF9WHVoELIyIFZLeDlwDHFHnGnOAOQDjyLfIRx4r5xyYmWabp7MXEOgbn72ACUDv+uzFH3pyTJuMPAvCZK+XAkBfjoHe/3vbezLT/OgvLsyV35oYk5lmjzHZaZ6P9bny276n8b/fVnkfShiUc63GFitanyvrciudtmv2Qi6Prs7+B9x2q3yLJK3d0JeZZkOOnpseZVfmlevG5SpTT0/2e/mh03fJTPPyK3fLl9/a7O9oW2//+sw0GzY8myu/gW13bng8erM/N15MW8LK3JEgLulw4HDg5OpjEbG0YvNm4PuSeiNii0/diJgPzAeYpMnl++tbFyi22IukI4FjgOVARMRZVcdPBXYElgH7A2fUCJQd1Yr6XFmXJU8VtOEXQF/BJ4p3oj4PexCXdBTwJuAzwE6SpgO/AvoiYrWkLwGnR0QfMBNYWiuAm40I0Xx3uqQJwCXAPhGxXtJ1ko6IiJsqkm0DnBIRIen9wJeBdxYud4u4Plu3CIL+AkG8U/V5uGen7w9cDSwBbgEmAl8DjgZWAeeSfEO5WNJSYBZw7HCW0WzImm+JHwg8EfHiGMAdwFHAi5U+Ik6vSN8D5BwQaT/XZ+sqgr5izxXuSH0e7olt95F8E2mUJt8gqtkIofq3pUyRtKRie37abTxoB2BNxfbqdN+WeUhbA8cDJxUoaku5Pls3SRZdbdgSH5H12Yu9mBXReMW2lRExu8HZy4FtK7Ynpfs2k1b4i4G/j4jfNFlSM8uQ0RIfkfU53/RpM6tJBBoYqPnK4S5guqSx6fbBwEJJkyVNApA0HvgGcEFE3Cfp3W35RcxGuSDoa/BfDh2pz26JmxXV5CpPEbFW0onARZJWAA9ExE2S5rFpTPlbwKuBGUpuO5oIXNeScptZhczu9MZnd6g+O4ibFVFgdjpARNwI3Fi1b27Fz8c0XzgzyysI+pSrxV3/Gh2oz6MqiD9+dvYiLgCTfpudJnIMRGy1Nt9Mxzz3Gb+wXfZiE70bsq+zZu8NucrEmuwFEj524O2Zaf51xVtyZffZHX6SmeZXG7Pfrrv15guoYzPW0sixbk4qIF/XubXQVbM+nCvdT1dm/0vm+bf+U1++utyXY7GQXSZk57g2Ryx5y4x8w6nP/fGlmWn2++QdmWniulty5ffC+7LX7Nn4zOLMNJr86lz5MWbbxseVb6Ge5BazjfnyHEFGVRA3azk/itSsSziIm41KDW4xM7OSCGCg4IptneAgblZEAP3lq/hmVs0tcbNRyGPiZt0gCPrDQdxsdHFL3KxLBANuiZuNNgElfAaxmW0ugIES1mUHcbMi3BI36w4RDLg73WwU8pi4WeklY+LFFnvpBAdxs0Ki6WVXzWwkSZZ7KZuuCeIve/UL/O31v2iY5uQr863YphyfycrR+MpzHYBQ9gpOW63PvljPxuw0k+/JXokN4LlZ2b/gv//PQZlpvv3mb+TK7zcbt8tM89YJ2V1dK/v/nCu/rDWccq/YFkB/+Sr+SPa6V23DHVft1zDN9z6U71p5HvUeOVZZG8j5Ra0nxzvnzzkae+tyvKWu/uUrc5QI/nLaU5lpHv2P12Wmmfa1ybnyG7Pswcw0W+/zN5lp1q59Ild+9GSEsRyfr4lgwC1xs9EmPCZu1gWCYGDAY+KZJB0JHEPynNWIiLOqjo8Dzgd+D8wEzo2IR4e7nGa5BMQobom7PlvXCNwSzyJpAnAJsE9ErJd0naQjIuKmimQnA09GxDxJs4DLgDcNZznNhmSUjom7Plt3KfYo0k7J8SyuljoQeCIi1qfbdwBHVaU5iuTh6kTEg8C+gw9UryZpjqQlkpb8adXobQ1ZB0UkY+K1Xt2vZfW5si6veK58XZpWfkEQsbHua6Qa7iC+A7CmYnt1um+oaQCIiPkRMTsiZr9kcr7HzZm1VhD9/TVfo0DL6nNlXZ66Xb7Jl2atlUxsq/caqYZ7THw5UPnw10npvqGmMRsZCs5OL/mYsuuzdZeCwboT9Xm4g/hdwHRJY9MuuIOBr0uaDPRFxGpgIUk33e3pGNr96X6zESeAyHMfUw1dMKbs+mxdpNiYeKfq87B2p0fEWuBE4CJJ5wAPpL/gacAn02QXknwwfAH4LPCx4Syj2ZBEoe70ls4RGW6uz9Z1or/+K1tH6rOiS2bWSloBVK4OMAVY2aHiFFXWsndTuadHxNSsEyXdkJ5fyzhgXcX2/IiYX3HuXwPvj4h3pdv/H3BYRHy4Is2v0jQ/T7d/l6Z5LPvXKqcadRm6671VBmUtN2xZ9lbUZRih9blrFnup/keStCQiZneqPEWUteyjsdwR8bYCWXtMuYZaH7ij8b3VSWUtNzRf9oJ1GTpUn4d7drqZbfLimHK6fTCwUNLkii62wTFlPKZsNqJ1pD53TUvcrGwiYq2kwTHlFaRjypLmAauAc0nGlM9Px5RfjseUzUakTtXnbg7i87OTjFhlLbvLPUQRcSNwY9W+uRU/vwCcNNzlGoH83hpeZS03jLL63DUT28zMzEYbj4mbmZmVlIO4mZlZSXXlmHjW0ncjlaS72XQfYn9EHNHJ8jQiaUfgHGDfiHh9um8kLxEK1C33CcAn2PS3vywiLu9MCa1SWesylKc+l7Uug+szdGEQz7n03Uh1Q0Sc2elC5HQIcD2wX8W+kbxE6KBa5Qb4QEQ8PvzFsXpKXpehPPW5rHUZXJ+7sjs9z9J3I9UsSadKOlPSiC5zRFzL5k+nghG8ROigOuUG+JSkv5N0Rrr2t3VemesylKQ+l7Uug+szdGFLnCE8ynQEOi8i7pHUC9wmaU1E3NbpQg1Bvb/9SF+cZBGwMCJWSHo7cA0wIrs+R5ky12Uod30ua12GUVafu7ElXtplKiPinvT//cDtwOGdLdGQlfJvHxFLI2JFunkzcGj6wWudVcr306CS1+fS/u1HW33uxiBec+m7DpYnF0l7SapcvWcmULaHXJRyiVBJX5I02Cs1E1iafvBaZ5WyLkNX1OdS1mUYffW567rT6y191+ly5bAaeIeknUm+9T4FXNXZItUn6VDgWGCndAnBr1CCJULrlHsZcLGkpcCs9Lh1WInrMpSoPpe1LoPrM3jFNjMzs9Lqxu50MzOzUcFB3MzMrKQcxM3MzErKQdzMzKykHMTNapC0o6RLJd2bI+2MdEnQ0yR9W9L/Ho4ympk5iJvVNrgms3KknQssjohzgfNIbnMxM2s7B3GzGmqtySxpH0nflPQ5SZdJ2iM99AwwNf15KnDfMBbVzEaxrlvsxayNLgU+GxF3SjqMpMV9NHAB8D1JFwAHAGd3rohmNpo4iJvl9xrgrZLeDIwHnk/3LwAujYirJE0Ffi1pj4hY1aFymtko4SBult/9wHcj4oF0Pe+j0/27AU+nPz8HDOChKjMbBl521ayGdE3m44C3AReTdJ3vDnwWWEoSuK+IiMWSDgFOBn4GzADui4hLOlFuMxtdHMTNRjlJOwLnAPtGxOtrHO8B/olk+GA6cFlE3D28pTSzWtydbmaDt9PtV+f4+4BJEXGapMnA3ZL27ubHO5qVhcftzEa5WrfTVTmK5NnepJP11gH7DEPRzCxD17TEp0zZPnafvluni2Elsfxn9zc8vgp4PiJzoZeXS7G2zrGn4b8j4m2Nzs/RlX0C8EbgN8DrgH+NiDuzytViO7B5kF+d7tuCpDnAHICJEyfuv9dee7W/dGYld999962MiKnZKbfUliBe64Mp/TD6BMm3eEjG1S6vce6RwDHAciAi4qw8ee4+fTeW3HFTC0pvo8HXxk9pePy8nNd5ATixzrEzoHEmiayu7F2AkyNinaQ3kNyrPitn8VplObBtxfakdN8WImI+MB9g9uzZsWTJkvaXzqzkJD3R7LntaonX+2D6QEQ8Xu8kSROAS4B9ImJ9uh71ERHh6GwjkihWiSLi2nThmHrH/7Fis4dN96a3laSJwISIWAEsBN4MXJ6OiY8DHh6OcphZY20ZE28wxvYpSX8n6Yz0w6DagcATEbE+3b6DZDzObMRSnRcwRdKSitecpvOQBHwGOKVwgbe89qHAscBOkr4gaTxwAptWnvsOsEbSF4EvA8d5UpvZyDCcY+KLgIURsULS24FrgCOq0uQee4PNx9+m7bZra0trllNv/UMrI2J20eunAfzLwIKIuKvo9apFxCKS+lnpaxXHB4BTW52vmRU3bLPTI2Jp2jUHcDNwqKTqz7/cY2/pNedHxOyImD116vatLbBZDoPd6bVeTV9Tmpgu30paRy4EfhARN0h6d8Eim1kXGbYgLulLkgY/22YCSwe75CTNSPffBUxPl7QEOJhkPM5sRBJJS7zWK9f52V3ZXwbeBZwl6VbgX1pWeDMrvXbNTt/sg4lkycplwMWSlpLMrj02TTsVWCxpz4hYK+lE4CJJK4AHPKnNRroi34RzdGWfQhvGwc2sO7QliNf5YLqwTtoVJLfRDG7fCNzYjnJZ93v+Cx/Nla6vRfkNtsTNzDqhaxZ7MesUB3Ez6xQHcbMC3BI3s05yEDcryA8gMLNOcRA3K8AtcTPrJAdxswKKLrtqZlaEP3/MCsp81JmZWZs4iJsV4O50M+skB3GzAtydbmad5M8fs4LcEjezTnEQt9Lov/3izDQXfeX7ua41IeN45LpK0hL3LWZm1ikO4mYF9fTUmdo2kPergJlZcxzEzQqQoLe3Tlt8oH94C2Nmo46DuFkhoqdeEN/oIG5m7eUgblaQ5DvFzawzHMTNCpCo3xI3M2szB3GzItSgOz3X6doROAfYNyJeX+N4D/BPwPPAdOCyiLi76QzNrKu0JYjX+mCSdCqwI7AM2B84IyJ+WePcu4F16WZ/RBzRjjKatUrd2en5HAJcD+xX5/j7gEkRcZqkycDdkvaOCA+4m1nbWuK1Ppi2AU6JiJD0fuDLwDtrnHtDRJzZpnKZtVTR7vSIuFbSYQ2SHAX8OE27StI6YB/ggaYzrUHSkcAxwPIkqzir6vgM4HzgXpJ6fWVE5Lsp38zapi1BvNYHU0ScXrHZQ9I9WMustNU+Hrg3IhbWy0fSHGAOwLTddi1UZuusgbv+LTPN2W89PTPNtjnzm5xxPH/FaNidPkXSkort+RExP/elEzsAayq2V6f7WkbSBOASYJ+IWC/pOklHRMRNFcnmAosj4p8lvRb4DuAgbtZhwz4mLmlr4HjgpDpJzouIeyT1ArdJWhMRt9VKmH4gzgeYvf9+XlnDhl1GS3xlRMwumMVyNv9uMind10oHAk9ExPp0+w6SHoDKIP4MMDX9eSpwX4vLYGZNGNZptWkAvxj4+4j4Ta00EXFP+v9+4Hbg8OErodnQSar5KnC9iZIGA+ZCkiBLOiY+Dni4cKE3l6e1fwHwBkkXAGcA/1HrQpLmSFoiacmKFStaXEwzqzZsQVzSeOAbwAURcZ+kd1ccm5H+fy9JH6s4bSbw2HCV0WzIJHp7e2q+8p2uQ4FjgZ0kfSGtJycAZ6dJvgOskfRFknkkx7VhUlue1v4C4NKIOAU4Grg6/VKxmYiYHxGzI2L21KlTqw+bWYu1a3b6Zh9MwFeAbwGvBmakrZSJwHVpi2OxpD1JWgDvkLQzyQfJU8BV7SijWSuIwhPbFgGLqnZ/reL4AHBq0xnkcxcwXdLYtEv9YODraZDui4jVwG7A02n654AB/OwXs45r18S2Wh9Mx9RJuwLYJd38A8m3fLNyEPT0lnvFtohYK+lE4CJJK4AHIuImSfOAVcC5wN8CJ0s6CJgBfD4iVnau1GYGXuzFrDAVu098RIiIG4Ebq/bNrfh5MbB4uMtlZo05iJsVoHRM3MysExzEzQry2ulm1ikO4tZW/d87J1e6BR/8l8w0O+a4zp9y5QbbZ9wCtlXkW3ZA8lPMzKxzHMTNCin2ABQzsyIcxM2KEPRs1dvpUpjZKOUgblaAJOSWuJl1iIO4WUHqcRA3s85wEDcrwi1xM+sgB3Gzgnp6PSZuZp3hIG5WgCS0lVviZtYZDuJmBUkO4mbWGQ7iZkUIetwSN7MOcRC3pj3xV0dmpvnJj3+e61p77/iSzDS/XJa9HtuYXLnBMxkrsm3MeZ1kYpvHxM2sMxzEzQoQ3fEUMzMrp7YEcUk7AucA+0bE69N944Dzgd8DM4FzI+LRGuceSfLs8eVARMRZ7SijWUsUbIlnvd8lzSCpN/cC+wFXRsT3my+wmXWTIQdxSdMi4smMZIcA15N86Aw6GXgyIuZJmgVcBryp6toTgEuAfSJivaTrJB0RETcNtZxmw6XZtdNzvt/nAosj4p8lvRb4DuAgbmYADOnTR9J04NasdBFxLbCmavdRwF3p8QeBfSVNqkpzIPBERKxPt+9IzzMbkSTRs1VvzVcOed7vzwBT05+nAve1pOBm1hWG1BKPiCck7dlkXjuweWBfne5bnSNNTZLmAHMApu22a5PFMiuo/qNIp0haUrE9PyLmV2zneb9fAHxP0gXAAcDZBUtrZl2kmTHxDwBXNXHecmDbiu1J6b6hpnlR+oE4H2D2/vvlewC0WSulLfE6VkbE7AZn53m/LwAujYirJE0Ffi1pj4hY1WyRzax71A3ikpYC1YFRJB80zQTxhSTdh7enY+L3R8TqNK8ZEbGUpLt9uqSxaRfjwcDXm8jLbHiIImun13y/S5oM9KX1Yzfg6TT9c8AAQxwGM7Pu1aglPi8iLpb0N8DNwG+BPUlm0jYk6VDgWGAnSV8AvgJcCJyfbr8c+FiadiqwWNKeEbFW0onARZJWAA94UpuNZEJNr51e7/0uaR6wCjgX+FvgZEkHATOAz0fEyhYV38xKrm4Qj4iL0x93jojfpD8/JilzVY6IWAQsqnHopBppVwC7VGzfCNyYlYe113Of+lBmmpfuuVNmmkP2z16gBeCh+5ZmpqmeBVnLc7lyy27K5r7zW8XuE6/1fo+IuRU/LwYWN52BmXW1PGPir5P0XuDXwCuAfdtbJLNy6YZHkea4X13A/0k3dwdeGhEfHdZCmtkW8gTxzwDzgH2Ah4FPt7VEZmUioOQrtuW8X/3DwB8j4pvpOa/pRFnNbHONJrZtExHPR8TjwPsq9k8cjoKZlUX9O8xKo9796pVB/EPADZI+DewIXDq8RTSzWhq1xM+VVGtm+ByS1dfMRj1JqLf0UTzP/erTgUkR8Q+SXkES0PeOiP7KRJut3TBtWhuLbGbQOIh/CHg7W87xmYSDuNkm5Q/iee5XXw38FCAiHk1XW9wNeLwy0WZrN8ye7bUbzNqsURCfGxH/Vr1T0kfaWB6zchGop/QT2/Lcr34TsAdAGsB7gWWdKrCZJRrdYrZFAE/3/0f7imNWPmUfE895v/p5wDxJnydZL+L4iFjXuVKbGfh54mbFlb87Pc/96n8CPj7c5TKzxhzER5mBn/57rnS9E7LfGvdclr0mzy4v3zFXfnn8Pkea/bYZm+tazz2/vuHx3B3kUqHFXszMihjyYJ6kXbJTmY0e6lXNl5lZuzW6T/y4OofeCby3PcUxKxlR/kFxMyutRn2mxwO3Aa8CNpA8AGUPYPwwlMusFARudZtZxzQK4p+OiIcl/V1EnD+4U9Lpw1Aus3LwmLiZdVCjW8weTn98ddWhvdpXHLPycW+6mXVKntnpv5D0EPAYMBO4or1FMiuZLniKmZmVU2YQj4jzJC0E9gZ+EREPFclQ0u4kqz89le6aRLK4xAkVaU4APgEMLiZxWURcXiRfs7Yo+DxxM7Mict0nngbuhyAJsBGxoECea4CPR8RP0uudRdUiE6kPpE9QMxvRikxs83O8zayIzCAu6YPAF4EpwAvABGBBsxlGxLPAYAAfC8yOiC/WSPopScvS/L4aEauazdOsbcSWjwjKe6qf421mBeVpiR9E0pX+ubRrfW7WCUPwQeCqGvsXAQsjYoWktwPXAEdUJ9rssYe77drCYpXTwL3Zy9rHE0/mutb4XbbJTLPV1tlvn1XL/pgrvw050kzJkeaJjJXY8ubXl+sqIISaHxP3c7zNrJA8nz6/i4gBYFy63coV294LXF29MyKWRsSKdPNm4FBJvTXSzY+I2RExe+rU7VtYLLOcRDKxrdYLpkhaUvGaU3X2UJ7jfRFJD9gNteqCmY1OeVriB0h6J7Be0k003Xm4OUmHA3dGxMZ0+8XHHkr6EnB6RPSRzIhfGhH9rcjXrLUEPXVj6sqImN3g5JY9x9vMRqc8s9OPAZD0I+ARkmcPt8IcNk3YATiNTY89XAZcLGkpMAs4tkV5mrWWgOZnp/s53mZWSK7Z6WlLfBLwc+DPrcg4Iv66arvysYcXtiIPs/YT9DbXu+3neJtZUXlmp88DppLMBXqE5IPl020ul1k5iKaDOPg53mZWTJ6JbX+MiI8Av42I/yFpIZjZIKn2y8yszfJ0pw/e2RPp/7etl9Bs1FHz3elmZkXlCeKPSnoEGJD0HuAbbS6TWYk4iJtZ5+QJ4lcCi0meXvZgRPyqvUWyWgYe/HZ2ogkTc1wo3516657Onr/4hk/+r8w0S3+wJFd+y5avzkyT5403IVduyRTvRiLj+ItEkcVezMwKyfPp8yhARFzrAG5Wg3pqv8zM2izPJ80VlU8uk/S6NpbHrFykRiu2mZm1VZ7u9JdKOhf4BUkv4ztJlks1M+iKMfGsp6lVpPsQcAWwbUQ8P4xFNLMa8gTx/YH/InkMIsDktpXGrGy6YHZ6zqepIWlv4FUdKaSZ1ZQniJ8YEXcPbkia2cbymJVP+e8Jz3yaWhro55IsPPP5ehfa7MmC06a1q7xmlsocuIuIuyVtJ2mapGkkj0Y0M9jUEq/1Ko88T1P7R+DsiGj4FNfNnyw4tcXFNLNqeZZdvQw4AFhBssjkNODM9hbLrETKP4mt4dPUJO0GbAe8T5t6HU6R9KOIyHcPoZm1RZ7u9IkRMWtwQ9Jh7SuOWclI0FP6IJ71NLWngBMGE6ePCr7AE9vMOi9PEL9X0oSIWJtub9fOAo1GA8/kaMyMyfFP9ee1mUni2edylAg2rlmfmeaWC3+YmeYV+03PlV+ex3LtnSPNQ9lJgKSp2TIlD+I5n6aGpKlsehjLXEnfiIjfd6bUZgYNgnj6LO8gWdzqbEnPpIcmAd8bhrKZjXyi9EEcsp+mlm6vAM5JX2Y2AjRq3s2LiIurd0r6WNFMJd3NpsZXf0QcUXV8HHA+8HtgJnBuRDxaNF+z1uuK7nQzK6lGQfwASWsj4j8rd0bEZS3I94aIOLPB8ZOBJyNinqRZwGXAm1qQr1nrlf8WMzMrqUZNiJXVAbyFZkk6VdKZko6qcfwoksk2RMSDwL6SWjqMadYyfp64mXVIo5Z4zQc5STohIhYUzPe8iLhHUi9wm6Q1EXFbxfF6961u9qirzRaW2G3XgkUya0LB2ele7tTMimgUxOekzw+vJJKJbQuKZBoR96T/75d0O3A4UBnEG963WnGd+cB8gNn775f76ZFmLdXkE8u83KmZFdXo0+e7JA87qX5dUSRDSXtVTY6bCTwmaXJFl/lCkqUgScfE74+I7AdOm3WC6rxgiqQlFa85VWfWW+5006U3LXdas4VuZqNbo5b4yoh4uHqnpFML5rkaeIeknUla2E8BV5Hcizp4T+qFwPmSvgC8HCg8I96sLRrfYrYyImY3OHtIy53K4+xmVqVREH+jpONrzE7Psy5HXRHxB+DoGofmVqR5ATipSD4jwcBTN+dL2JNjIZfeHGlyfMgPrOvPUSCYOD17HuFR//mpzDSXH//VXPmNy5HmFznSbJudBIAJGcfzd5Cr6e50vNypmRVUNzJExJuHsyBmpdV8C9nLnZpZIV6lwqyoHtV+ZUiXMh5c7vQc0uVOgdOATw6mkzQ1HVqCZLnTXdrwW5hZCeVZO93M6lGh7nQvd2pmhTiImxWVo9VtZtYODuJmRXnWuJl1iIO4WVEFutPNzIpwEDcrouCyq2ZmRTiImxXl7nQz6xAHcbOiHMTNrEMcxJs08NsfZifqzbMOGflWY4scz3cZl51f7+475ygQrL33N5lpbvqHr2em2SZXboNLjTc2JUeap3PmNznjeP6wXOwWMzOzIhzEzYoQ0NPb6VKY2SjlIG5WyKZHlpmZDTcHcbOi3BI3sw5xEDcrpDvGxCUdCRxD8hS1iIizqo6fCuwILAP2B86IiF8Oe0HNbDMO4mZFCFC5W+KSJgCXAPtExHpJ10k6In0Yy6BtgFMiIiS9H/gy8M5OlNfMNhnWIC5pT5KHOPwM2BV4NiL+oSrNCcAngMHnll8WEZcPZznNhqT8t5gdCJKQTjUAAAz5SURBVDyRPg4V4A7gKODFIB4Rp1ek7wH8OFSzEWC4W+KTgW9HxPUAkh6RtDAi7qtK94GIeHyYy2bWBJW+JQ7sAKyp2F6d7tuCpK2B44GT6hyfA8wBmDZtWmtLaWZbGNYgHhH3Vu3qAf5cI+mnJC0DJgBfjYhVbS+cWbPKPya+HNi2YntSum8zaQC/GPj7iKi5kEBEzAfmA8yePTvH4gZmVkTHxsQlHQ38d43JMYuAhRGxQtLbgWuAI+pcY9O3/t12bVnZBpYsyE40eWp2mo21vp/UsFWORWF6c7T28iwIs/122WmAGMi+1uH/968y01x+zvdy5ZdnWZwtokqT14HsvuCBnNfpkoltdwHTJY1Nu9QPBr4uaTLQFxGrJY0Hvg6cHxEPS3p3RFzXyUKbWYeCuKTDgcOBk6uPRcTSis2bge9L6o2I/hppN33r338/f+u34SdQgSA+EmaFR8RaSScCF0laATwQETdJmgesAs4FvgW8GpihZA7ARMBB3KzDhj2ISzoKeBPwGWAnSdOBX7HpG/+XgNMjog+YCSytFcDNRobmx8RH0qzwiLgRuLFq39yKn49pdZ5mVtxwz07fH7gaWALcQvJt/mvA0Wz6xr8MuFjSUmAWcOxwltFsyJpf7MWzws2skOGe2HYfGc/EiIgLh6k4Zi3QcNnVKZKWVGzPT4eABrVsVriZjU5e7MWsiMYPQFkZEbMbnN2yWeFmNjqVflqtWWels9NrvbK9OCs83T4YWChpsqRJAOms8G8AF0TEfZLe3ZZfw8xKyS1xs6KanNjmWeFmVpSDuFlRBZZd9axwMytiVAXx/m+fnp0I0F6vzJEqx23pWzecw1eRYY6u1zWrs9NsNSYzyYbb789RINh6u7GZaX42/6bMNG/ca+dc+S3+5R8y0+yU4zp5l/bbmHE8/6IDXbHsqpmV1KgK4vb/2rvzGEnKOozj30fkWM5lZQ0QkENWJLiAEQjIKXiAiIoQMEFwgwQwiiJBICqHnCvCIijXCoGAgYguGgiE0yCgIAIRxCOArJweICggyrE8/vHWuL2zOzs12zPV1c3zSSbT1V3d/UxPd/+6qt7+vTHuxCB0bIuIPpUiHtGVxX7FLCJiQqWIR3Qru9MjokdSxCO6MhAToEREn0oRj+hWinhE9EiKeES3uviKWUREN1LEI7qh7E6PiN5JEY/oVga2RUSPpIhHdEVkCoKI6JWBKeLP33c/cyattth1PnlJzVkcax3jrLFO7WOlNfqDLb3M6Ou8dfR/57K7blMjD8y74+5R19n0MzuMus6c06+udX+LnH9zmAdrrLPS6KsAoz/i9Tu2gXJMPCJ6pPEiLumDwKcoUy7a9jeHXb4ccDrwFDANmGn7oaZzRtSWY+IR0SONFnFJywPnAxvbfkXSHEk72+5swn0Y8Ljt0yRNBy4CtmsyZ0RtSu/0iOidpjchtgYes/1KtfwLYLdh6+xGmWcZ278FNh2aWzminTTCT0TExGp6d/rbgRc7ll9g4cOhI62z0DRekg4CDgJY/NHwiAmU3ekR0SNNv/v8nQXHHq1cnTfWdQCwPdv25rY3z6Z69Eb1PfFF/URETLCmt8TvBNaRtGy1S30b4FxJU4DXbb8AXEvZ7X57dUz8/ur8iHbqomC3ZaBnW3JExNg0WsRtvyzp88DZkp4BHrB9i6TTgOeAmcBZwOmSvgFsAHyuyYwRY7PkHdvaMtCzLTkiYuwa/4qZ7ZuAm4add2TH6f8ANb/QHdFjopst8ZEGenYWz92Ar0EZ6ClpU0krj/PeqbbkiIgxGphmL4/Cs3vBYx1nrQY8u8BKM85pNFMXFs7eHwYp9zp1rnjvffffoElTRxpXuZykezqWZ9ue3bE8rgM9uzBuOToHmwKvSKrTo6eX2v6cbXs+aH/GtucD2HBJrzgwRdz21M5lSffY3rxXebrRr9nfjLlt79LFXY/rQM825Kg+pMyG/ng+tD1j2/NB+zO2PR+UjEt63Qyhjeid/w/0rJa3Aa6VNKWjN8LQQE8mcKBnW3JExBgNzJZ4RL9py0DPtuSIiLEb5CI+e/RVWqtfsyf3GLVloOcE5eiH50PbM7Y9H7Q/Y9vzQRcZZY9lvqaIiIhoixwTj4iI6FMp4hEREX1qII+Jj9ZCsq0k3QX8t1qcZ3vnXuZZHEmrAycBm9reojqv9a05R8g9AziE+Y/9RbYv603C/tP2lq018h0FrA78FXgfcKztPzaVr07GjvX2BX4ArGT7pbbkkyTg0GpxXWCy7QOaylcz43qU5+Gvgc2Ay21f3WC+hd57hl3+FuAU4CVKn4qLbN816g3bHqgfYHngEWDZankOsHOvc9XMfnyvM4wh617A7sA9HecdDRxZnZ4O3N7rnDVzzwDW7XW2fvyp83rr5fOiZr4TmT8+aB/gmrY9htX5GwEnAwZWbFM+YD9g/47lTdr2GALnAV+pTr8XeLjhjAu99wy7/NPAudXpKcBDwFKj3e4g7k6vM2d5W02XdJSk4yW1OrPtH7NgBy/og7ngR8gN8EVJR0g6tpqQJ+qp83rr5fNi1Hy2j3H1zkk5xNjYFm5l1IxVf/sjgV7sVazzP94XmCLpS5KGtiabVCfj34ChpmBTgXsbygYs9r1nSOfr5DnKnsGNR7vdQdydXqeFZFt9y/bdkpYCbpP0ou3beh1qDJpoEToRfg5ca/sZSR8FfgS09lBGy7SldexIar8fSFoG+CzNz91QJ+PJwIm2Xy17rhtVJ986wMq2T5D0LuB6SRvZnteijLOAn0iaBWxJ2QPTJktUuwaxiDfRpnJC2L67+j1P0u3AB4B+KuJ9+djbntux+DPgaklLNfgG1M/a0jp2JLXuuyrg5wFft/2nhrINWWxGSWsDqwJ7dxTwwyVdZ3uJ23WOV77KC8CvAGw/VO1pWRv4cwP5oF7GS4ALbV8haSrwsKT1q63eNlii18kg7k5fZAvJHuapRdK7JXV2wZpGOcbTT/qyNaekUyUNfaCdBsxNAa+t7S1bR80naRJwATDL9r2S9mwoW62Mtp+wPcP2TNszq3VmNVTAR81XnXcLsD5Add5SlIGCTamTcW3gL9Xp54E36HENlLRC9YECFnydTAGWA3436m3MPxQ0OCR9iDKI4BngNffB6HRJawLnAPdRPoEtDRxu+42eBhuBpB2A/YFdKFswZ1QXnU55oWwAnOL2jU5fVO6DgPcAcykDr85ynVGhASz69TbUstX2zKpI9ux5USPfVZT//9PVVVbwIkYP9zJjtc5U4GDKbuATgQtsP9WGfJJWAU6jzCT5TmCO7euayDaGjNsCh1HeY9cD7rV9foP5FvXecwAw3fYh1ej0U4GXgXcA36/zPjSQRTwiIuLNYBB3p0dERLwppIhHRET0qRTxiIiIPpUiHhER0adSxCMiIvrUIDZ7aSVJ2wMnAMsAO9h+TdJalIb4kymTLjwwTvf1IHA95XubWwA/pHxt7WlKj+Etbe84Hve1mAzbAmdTviZ360TeV0TEm1WKeENs3ybpVko7z+8AX7D9pKRLKJNvjEsBr5xh+2JJHwOm2D5C0tsoDRAeoLQcnFC275A0nn9TREQMkyLevIOByyXtb/vSoTMlzQS2sr2jpL2B2bYnS9qa0hjgdsr/azPg25SWrJsDhw7v3GT74uF3avsflHai6wKTJB1PmXbxPtvHSdodOBO4htJtaQ/ba0s6obrfecCLtk+TtCJl6/42YEPKlH43V3/H2ZRGNY8Ca3X8fd+jNGGYBDxl+7tL/AhGRASQIt4LLwN7UCY46dxSPR/YCsD2lVWnIWzfKemnlCnpjpF0GKXA7idpD8qEDWNtv7gGZdc+wOPAcbavqdpNPmz7XEmXSvoI5YPFhwEk3SrpRsoUeWfavrlqD3gDcHM189o027tW63+i+r0q8HFga9tPSXr/GPNGRMQipIj3gO25kmYAVwJH1bza0KQM/+w4/TwLNsyva+5QO1dJrw+77A9VxnskfRVYXtLR1WVPUKbwexjYsdpL8Brzp/fbuLpsyKPVbT0v6cvAhVULzpOWIHNERAyTIt4jtm+RdD5l8NcxlCnohiZkWI75hbGWqu/uWrYfr3P3NS+7n7L1PNS7eSfKpCwHAmvaPkDS0sAh1fq/B3bquP7QhAiTgWds7yppY+AKYJMaOSMiYjFSxBtSjdbeHlhR0nG2/217lqTNoByzlvQbSadQtmD/JekQytSY2wPTJf0S2B1YtZqzdz9gE0lbAq8Cl1Em8EDSGsA+lJl99rQ9p4pyYHXezpQPDatIOgB4kFJY95P0pO1HbN8oaUtJpwKvU2bVOZqy+3wvSd8GnqtuY0/gKmBXSRdSttpVZZwLHCZpO2A1ysC+iIjoUiZAiYiI6FNp9hIREdGnUsQjIiL6VIp4REREn0oRj4iI6FMp4hEREX0qRTwiIqJPpYhHRET0qf8B0k1yJsAztfMAAAAASUVORK5CYII=\n",
- "text/plain": [
- "<Figure size 576x432 with 7 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Example 10\n",
- "import matplotlib.pyplot as plt\n",
- "matrix=np.loadtxt(open(\"data/heatmap.csv\", \"rt\"), delimiter=\",\", skiprows=1,usecols=(np.arange(5,21))).T\n",
- "# Create a figure and get axis\n",
- "fig = plt.figure()\n",
- "ax1 = fig.add_subplot(221) \n",
- "ax2 = fig.add_subplot(222)\n",
- "ax3 = fig.add_subplot(223)\n",
- "ax4 = fig.add_subplot(224)\n",
- "fig.set_size_inches(8,6)\n",
- "hm1 = ax1.imshow(matrix, origin='lower')\n",
- "hm2 = ax2.imshow(matrix, cmap=\"inferno\", origin='lower')\n",
- "hm3 = ax3.imshow(matrix, cmap=\"OrRd\", origin='lower')\n",
- "## associate colorbars\n",
- "cbar1 = fig.colorbar(hm1, ax=ax1); cbar2 = fig.colorbar(hm2, ax=ax2); cbar3 = fig.colorbar(hm3, ax=ax3)\n",
- "plt.suptitle(\"L3 Total cache misses per core\")\n",
- "ax3.set_xlabel(\"Num.Threads\")\n",
- "ax1.set_ylabel(\"Thread Id.\"); ax3.set_ylabel(\"Thread Id.\")\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Multi plot\n",
- "\n",
- "- Subplot\n",
- "- GirdSpec\n",
- "- Arrangements 1\n",
- "- Arrangements 2\n",
- "- Histogram multiplot\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 233,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFoCAYAAACsbHn1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3W2MXOV5//HvL6A4sYPbWl1EI4hLAi3IIYlhU4k4hRemgpRElUiVRCIhKJFcUNqqjRBBSkKh5MFyKWl5EQwNlaWkrdrGrfrg9CEyUtUgp7CLKG2kCLCw29BSb0Qlg9y4lXv9X+xxGZa15+zOMnPO/L8fyfLc97ln57drLq45Z845m6pCkiT102smHUCSJK2ejVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqsTOHLUhyDvA54O1V9c5ltr8G+ALwIrAZeLCqvt1suwq4DjgCVFXduYbZJa2Q9SxNn6GNHHg38GfAO06x/QPAxqq6Lckm4NtJLgbWAbuBLVV1PMneJNurav+aJJe0GtazNGWGHlqvqq8DL5xmybXAgWbt88APgC3A5cDhqjrerHu4WStpQqxnafq02SMf5mxe/j+Go83czCnmJXWX9Sz1zFo08iPAWQPjjc1cnWJ+WUl2ADsANmzYcNlFF120BtGk6TU/P//9qppZ4y87cj1by9LKjVLPq2rkSTYA66tqAdgHXAF8tflM7XXAd1j8TG1zknXN4bhtwJdP9TWr6gHgAYDZ2dmam5tbTTTp/xtJDq/R11nTeraWpZUbpZ7bnLV+JfAR4MeSfAb4TeBG4BLgJuCPgK1Jfg14E3BDVZ0AjiW5Gbg3yQLwhCfGSJNlPUvTJ1387We+i5eGSzJfVbOTznE61rLUzij17A1hJEnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj53ZZlGSq4DrgCNAVdWdS7Y/CLxlYOptwKVVdSjJIeBQM/9sVV0/amhJq2MtS9NnaCNPsh7YDWypquNJ9ibZXlX7B5b9bVX9YbN+I7Cnqg412/ZU1R1rnFvSClnL0nRqc2j9cuBwVR1vxg8D1w4uOFn4jY8DvzswviLJrUnuSvKukdJKGoW1LE2hNofWzwZeGBgfbeZeIclrgKuB3xqYvq2qHmn2Bh5L8t6qenq1gSWtmrUsTaE2e+RHgLMGxhubueX8HPCXVVUnJ6rqkebvY8DjwLblnphkR5K5JHMLCwttsktaGWtZmkJtGvkBYHOSdc14G7AvyabmM7RBNwJ7Tg6SbE9yzcD2C4CDy71IVT1QVbNVNTszM9M2v6T2rGVpCg09tF5Vx5LcDNybZAF4oqr2J9kFPA/sBEjyDuDJqnpx4OlHgDuSXAq8EdhbVd9a8+9C0lDWsjSdMnDkrDNmZ2drbm5u0jGkTksyX1Wzk85xOtay1M4o9ewNYSRJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo+d2WZRkquA64AjQFXVnUu23wjcBPygmXqwqr7abPswsBU4ARysqvvXJrqklbKWpekztJEnWQ/sBrZU1fEke5Nsr6r9S5Z+qKoOLXnuucAtwNaqqiSPJnmoqp5aq29AUjvWsjSd2hxavxw4XFXHm/HDwLXLrPvFJLckuT3JpmbuamC+qqoZHwDeM1JiSatlLUtTqM2h9bOBFwbGR5u5QX8H7KuqhSQ/C/wxsL3lcyWNh7UsTaE2e+RHgLMGxhubuf9TVc9U1UIzfAi4MskZbZ57UpIdSeaSzC0sLCy3RNJorGVpCrVp5AeAzUnWNeNtwL4km5JsBEjyxSQn9+4vBJ6pqhPA3wCXJUmz7XLgr5Z7kap6oKpmq2p2ZmZmtd+PpFOzlqUpNPTQelUdS3IzcG+SBeCJqtqfZBfwPLATeA64L8kzwCXAR5rnfi/J3cCXkpwAvuLJMdJkWMvSdMpL5650x+zsbM3NzU06htRpSearanbSOU7HWpbaGaWevSGMJEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqsTPbLEpyFXAdcASoqrpzyfZPAecAzwGXAbdX1XebbYeAQ83SZ6vq+jVJLmnFrGVp+gxt5EnWA7uBLVV1PMneJNurav/AsjcAn6yqSvJB4DeA9zXb9lTVHWsdXNLKWMvSdGpzaP1y4HBVHW/GDwPXDi6oqs9WVQ18zRcHNl+R5NYkdyV518iJJa2WtSxNoTaH1s8GXhgYH23mXiHJa4GPAp8YmL6tqh5p9gYeS/Leqnp6tYElrZq1LE2hNnvkR4CzBsYbm7mXaQr/PuDTVXXw5HxVPdL8fQx4HNi23Isk2ZFkLsncwsJC++9AUlvWsjSF2jTyA8DmJOua8TZgX5JNSTYCJHk9cD9wT1XNJ3l/M789yTUDX+sC4CDLqKoHqmq2qmZnZmZW+/1IOjVrWZpCQw+tV9WxJDcD9yZZAJ6oqv1JdgHPAzuB3wPeCpyfBGADsJfFd/t3JLkUeCOwt6q+9ep8K5JOx1qWplNeOq+lO2ZnZ2tubm7SMaROSzJfVbOTznE61rLUzij17A1hJEnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj53ZZlGSq4DrgCNAVdWdS7a/DrgbeBa4ENhZVU822z4MbAVOAAer6v61iy9pJaxlafoMbeRJ1gO7gS1VdTzJ3iTbq2r/wLJfAf6lqnYluQR4EPjpJOcCtwBbq6qSPJrkoap66tX4ZiSdmrUsTac2h9YvBw5X1fFm/DBw7ZI11wIHAKrqn4C3J9kIXA3MV1U16w4A7xk5taTVsJalKdSmkZ8NvDAwPtrMtVnT5rmSxsNalqZQm8/IjwBnDYw3NnNt1hwBLlgy//RyL5JkB7CjGR5P8s8tsk3KjwLfn3SIIbqesev5oPsZf3KF663l5XX937nr+aD7GbueD1Zezy+pqtP+AdazWLDrmvFeYDuwCdjYzN0G3No8vgT4++bxucDjQJrxo8CFLV5zbtiaSf7per4+ZOx6vj5kXGk+a7mfGbuerw8Zu55v1IxD98ir6liSm4F7kywAT1TV/iS7gOeBncBvA3cn+QyL79o/3jz3e0nuBr6U5ATwlfLkGGkirGVpOrW6/Kyqvgl8c8ncrQOP/wv4xCme+zXgayNklLRGrGVp+nT1hjAPTDrAEF3PB93P2PV80P2MXc8HZlwLXc8H3c/Y9XwwQsaTn3dJkqQe6uoeuSRJaqHVZ+SvhlFuFdmhjJ8CzgGeAy4Dbq+q73Yl38C661n8bPOsqnpxXPma1x72MwzwS83wx4EfrqqPdSzj+Sz+t/go8A7g96vqz8eY7xzgc8Dbq+qdy2x/DfAF4EVgM/BgVX17XPmaDJ2u567XcpuMA+us59Xnm85antBp9steBrNkzbKXwXQs41289PHEB4G/6FK+Zv5i4PNAAW/o4M/wI8ANA+O3dTDjfcCvNo+3Ak+NOePPA+/jFJenAB8Cvtw83gQ8CZzRsZ/hxOq567XcNmMzbz2Plm8qa3lSh9ZHuVXkuAzNWFWfreYnzuLHFON8dzw0X3Nv7VuBZd/Zj0Gbf+frgU1JfjnJyXei49Qm438AM83jGWB+TNkAqKqv8/K7qi01WCvPAz8Atowh2kldr+eu1zJYz+PKN5W1PKlD66PcKvLoqxtt6Ou/QpLXAh/lFJftvEra5Ps8cFdV/ffiEa+xa5NxM4s3I/n1JD8B/HWSi6vqRIcy3gP8aZJ7gJ9ice+tSyZ9+9Su13PXaxms53Hlm8panlQjH+VWkePS6vWbwr8P+HRVHRxTNhiSL8l5wI8AHxgo+k8m+UZVzXUhY+Mo8A8AVfVks5d2HnBoHAFpl3EPizdA+YMkM8BTSd7cvGPugj7UyiQzdr2WwXoeV749TGEtT+rQ+gFgc5J1zXgbsC/JpoHDbftYPFRC8+sU/7GqxrU33ipjktcD9wP3VNV8kvd3JV9V/WtV3VhVO6tqZ7PmnjEW/dCMzdx+4M0AzdwZLJ5w1KWM5wH/3jz+T+B/mfAVH0k2NP8jgpfXyibgdcB3xhin6/Xc9VoemtF6XrN8U1nLE7uOPMnPsPjB/wLwP1V158lbRVbVzqaw7mbxh34B8IUa/1nrwzL+CfBW4N+ap2yoZc5EnFS+Zs0M8AssHkK6C7i/qp7tSsYkPwTsAg4DbwH2VtU3xpWvZcZ3s/h7uh8Dzmfx13nuHmO+K4EbgGtY3GP8TeBjwCVVdVNzpusXgWPAm4DfqfGftd7peu56LbfJ2KyxnkfLN5W17A1hJEnqsaGfkY9y3duwa/okjZf1LE2fNie7vRv4MxYvnl/OB1g8S/G25pj+t5NcDKwDdgNbqup4kr1JtlfV/jVJLmk1rGdpygz9kH+E697aXNMnaYysZ2n6rMXlZ6e67m3mFPOSust6lnpmLRr5qa57q1PMLyvJDmAHwIYNGy676KKL1iCaNL3m5+e/X1Uzw1euyMj1bC1LKzdKPa+qkSfZAKyvqgUWr3u7Avjqkuve1tFc09ccjtsGfPlUX7OqHqD5fayzs7M1NzfOyyOl/klyeI2+zprWs7Usrdwo9dzmrPUrWbwR/o8l+QyL173dyOIvPrgJ+CNga5JfY/G6txua2/EdS3IzcG+SBeAJT4yRJst6lqZPJ68j9128NFyS+aqanXSO07GWpXZGqeeJ3ppOkiSNxkYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUYzZySZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUY2e2WZTkKuA64AhQVXXnku0PAm8ZmHobcGlVHUpyCDjUzD9bVdePGlrS6ljL0vQZ2siTrAd2A1uq6niSvUm2V9X+gWV/W1V/2KzfCOypqkPNtj1Vdcca55a0QtayNJ3aHFq/HDhcVceb8cPAtYMLThZ+4+PA7w6Mr0hya5K7krxrpLSSRmEtS1OozaH1s4EXBsZHm7lXSPIa4Grgtwamb6uqR5q9gceSvLeqnl5tYEmrZi1LU6jNHvkR4KyB8cZmbjk/B/xlVdXJiap6pPn7GPA4sG25JybZkWQuydzCwkKb7JJWxlqWplCbRn4A2JxkXTPeBuxLsqn5DG3QjcCek4Mk25NcM7D9AuDgci9SVQ9U1WxVzc7MzLTNL6k9a1maQkMPrVfVsSQ3A/cmWQCeqKr9SXYBzwM7AZK8A3iyql4cePoR4I4klwJvBPZW1bfW/LuQNJS1LE2nDBw564zZ2dmam5ubdAyp05LMV9XspHOcjrUstTNKPXtDGEmSesxGLklSj9nIJUnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GM2ckmSesxGLklSj9nIJUnqMRu5JEk9ZiOXJKnHbOSSJPWYjVySpB6zkUuS1GNntlmU5CrgOuAIUFV155LtNwI3AT9oph6sqq822z4MbAVOAAer6v61iS5ppaxlafoMbeRJ1gO7gS1VdTzJ3iTbq2r/kqUfqqpDS557LnALsLWqKsmjSR6qqqfW6huQ1I61LE2nNofWLwcOV9XxZvwwcO0y634xyS1Jbk+yqZm7GpivqmrGB4D3jJRY0mpZy9IUanNo/WzghYHx0WZu0N8B+6pqIcnPAn8MbG/5XEnjYS1LU6jNHvkR4KyB8cZm7v9U1TNVtdAMHwKuTHJGm+eelGRHkrkkcwsLC8stkTQaa1maQm0a+QFgc5J1zXgbsC/JpiQbAZJ8McnJvfsLgWeq6gTwN8BlSdJsuxz4q+VepKoeqKrZqpqdmZlZ7fcj6dSsZWkKDT20XlXHktwM3JtkAXiiqvYn2QU8D+wEngPuS/IMcAnwkea530tyN/ClJCeAr3hyjDQZ1rI0nfLSuSvdMTs7W3Nzc5OOIXVakvmqmp10jtOxlqV2RqlnbwgjSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUYzZySZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUYzZySZJ67Mw2i5JcBVwHHAGqqu5csv1TwDnAc8BlwO1V9d1m2yHgULP02aq6fk2SS1oxa1maPkMbeZL1wG5gS1UdT7I3yfaq2j+w7A3AJ6uqknwQ+A3gfc22PVV1x1oHl7Qy1rI0ndocWr8cOFxVx5vxw8C1gwuq6rNVVQNf88WBzVckuTXJXUneNXJiSatlLUtTqM2h9bOBFwbGR5u5V0jyWuCjwCcGpm+rqkeavYHHkry3qp5ebWBJq2YtS1OozR75EeCsgfHGZu5lmsK/D/h0VR08OV9VjzR/HwMeB7Yt9yJJdiSZSzK3sLDQ/juQ1Ja1LE2hNo38ALA5ybpmvA3Yl2RTko0ASV4P3A/cU1XzSd7fzG9Pcs3A17oAOMgyquqBqpqtqtmZmZnVfj+STs1alqbQ0EPrVXUsyc3AvUkWgCeqan+SXcDzwE7g94C3AucnAdgA7GXx3f4dSS4F3gjsrapvvTrfiqTTsZal6ZSXzmvpjtnZ2Zqbm5t0DKnTksxX1eykc5yOtSy1M0o9e0MYSZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUYzZySZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUY2e2WZTkKuA64AhQVXXnku2vA+4GngUuBHZW1ZPNtg8DW4ETwMGqun/t4ktaCWtZmj5DG3mS9cBuYEtVHU+yN8n2qto/sOxXgH+pql1JLgEeBH46ybnALcDWqqokjyZ5qKqeejW+GUmnZi1L06nNofXLgcNVdbwZPwxcu2TNtcABgKr6J+DtSTYCVwPzVVXNugPAe0ZOLWk1rGVpCrVp5GcDLwyMjzZzbda0ea6k8bCWpSnU5jPyI8BZA+ONzVybNUeAC5bMP73ciyTZAexohseT/HOLbJPyo8D3Jx1iiK5n7Ho+6H7Gn1zhemt5eV3/d+56Puh+xq7ng5XX80uq6rR/gPUsFuy6ZrwX2A5sAjY2c7cBtzaPLwH+vnl8LvA4kGb8KHBhi9ecG7Zmkn+6nq8PGbuerw8ZV5rPWu5nxq7n60PGrucbNePQPfKqOpbkZuDeJAvAE1W1P8ku4HlgJ/DbwN1JPsPiu/aPN8/9XpK7gS8lOQF8pTw5RpoIa1maTq0uP6uqbwLfXDJ368Dj/wI+cYrnfg342ggZJa0Ra1maPl29IcwDkw4wRNfzQfczdj0fdD9j1/OBGddC1/NB9zN2PR+MkPHk512SJKmHurpHLkmSWmj1GfmrYZRbRXYo46eAc4DngMuA26vqu13JN7DuehY/2zyrql4cV77mtYf9DAP8UjP8ceCHq+pjHct4Pov/LT4KvAP4/ar68zHmOwf4HPD2qnrnMttfA3wBeBHYDDxYVd8eV74mQ6frueu13CbjwDrrefX5prOWJ3Sa/bKXwSxZs+xlMB3LeBcvfTzxQeAvupSvmb8Y+DxQwBs6+DP8CHDDwPhtHcx4H/CrzeOtwFNjzvjzwPs4xeUpwIeALzePNwFPAmd07Gc4sXruei23zdjMW8+j5ZvKWp7UofVRbhU5LkMzVtVnq/mJs/gxxTjfHQ/N19xb+1Zg2Xf2Y9Dm3/l6YFOSX05y8p3oOLXJ+B/ATPN4BpgfUzYAqurrvPyuaksN1srzwA+ALWOIdlLX67nrtQzW87jyTWUtT+rQ+ii3ijz66kYb+vqvkOS1wEc5xWU7r5I2+T4P3FVV/714xGvs2mTczOLNSH49yU8Af53k4qo60aGM9wB/muQe4KdY3HvrkknfPrXr9dz1WgbreVz5prKWJ9XIR7lV5Li0ev2m8O8DPl1VB8eUDYbkS3Ie8CPABwaK/pNJvlFVc13I2DgK/ANAVT3Z7KWdBxwaR0DaZdzD4g1Q/iDJDPBUkjc375i7oA+1MsmMXa9lsJ7HlW8PU1jLkzq0fgDYnGRdM94G7EuyaeBw2z4WD5XQ/DrFf6yqce2Nt8qY5PXA/cA9VTWf5P1dyVdV/1pVN1bVzqra2ay5Z4xFPzRjM7cfeDNAM3cGiyccdSnjecC/N4//E/hfJnzFR5INzf+I4OW1sgl4HfCdMcbpej13vZaHZrSe1yzfVNbyxK4jT/IzLH7wvwD8T1XdefJWkVW1symsu1n8oV8AfKHGf9b6sIx/ArwV+LfmKRtqmTMRJ5WvWTMD/AKLh5DuAu6vqme7kjHJDwG7gMPAW4C9VfWNceVrmfHdLP6e7seA81n8dZ67x5jvSuAG4BoW9xh/E/gYcElV3dSc6fpF4BjwJuB3avxnrXe6nrtey20yNmus59HyTWUte0MYSZJ6bOhn5KNc9zbsmj5J42U9S9Onzclu7wb+jMWL55fzARbPUrytOab/7SQXA+uA3cCWqjqeZG+S7VW1f02SS1oN61maMkM/5B/hurc21/RJGiPrWZo+a3H52amue5s5xbyk7rKepZ5Zi0Z+quve6hTzy0qyA9gBsGHDhssuuuiiNYgmTa/5+fnvV9XM8JUrMnI9W8vSyo1Sz6tq5Ek2AOuraoHF696uAL665Lq3dTTX9DWH47YBXz7V16yqB2h+H+vs7GzNzY3z8kipf5IcXqOvs6b1bC1LKzdKPbc5a/1KFm+E/2NJPsPidW83sviLD24C/gjYmuTXWLzu7YbmdnzHktwM3JtkAXjCE2OkybKepenTyevIfRcvDZdkvqpmJ53jdKxlqZ1R6nmit6aTJEmjsZFLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT12JltFiW5CrgOOAJUVd25ZPuDwFsGpt4GXFpVh5IcAg41889W1fWjhpa0OtayNH2GNvIk64HdwJaqOp5kb5LtVbV/YNnfVtUfNus3Anuq6lCzbU9V3bHGuSWtkLUsTac2h9YvBw5X1fFm/DBw7eCCk4Xf+DjwuwPjK5LcmuSuJO8aKa2kUVjL0hRqc2j9bOCFgfHRZu4VkrwGuBr4rYHp26rqkWZv4LEk762qp1cbWNKqWcvSFGqzR34EOGtgvLGZW87PAX9ZVXVyoqoeaf4+BjwObFvuiUl2JJlLMrewsNAmu6SVsZalKdSmkR8ANidZ14y3AfuSbGo+Qxt0I7Dn5CDJ9iTXDGy/ADi43ItU1QNVNVtVszMzM23zS2rPWpam0NBD61V1LMnNwL1JFoAnqmp/kl3A88BOgCTvAJ6sqhcHnn4EuCPJpcAbgb1V9a01/y4kDWUtS9MpA0fOOmN2drbm5uYmHUPqtCTzVTU76RynYy1L7YxSz94QRpKkHrORS5LUYzZySZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9ZiNXJKkHrORS5LUYzZySZJ6zEYuSVKP2cglSeoxG7kkST1mI5ckqcds5JIk9diZbRYluQq4DjgCVFXduWT7jcBNwA+aqQer6qvNtg8DW4ETwMGqun9toktaKWtZmj5DG3mS9cBuYEtVHU+yN8n2qtq/ZOmHqurQkueeC9wCbK2qSvJokoeq6qm1+gYktWMtS9OpzaH1y4HDVXW8GT8MXLvMul9MckuS25NsauauBuarqprxAeA9IyWWtFrWsjSF2hxaPxt4YWB8tJkb9HfAvqpaSPKzwB8D21s+V9J4WMvSFGqzR34EOGtgvLGZ+z9V9UxVLTTDh4Ark5zR5rknJdmRZC7J3MLCwnJLJI3GWpamUJtGfgDYnGRdM94G7EuyKclGgCRfTHJy7/5C4JmqOgH8DXBZkjTbLgf+arkXqaoHqmq2qmZnZmZW+/1IOjVrWZpCQw+tV9WxJDcD9yZZAJ6oqv1JdgHPAzuB54D7kjwDXAJ8pHnu95LcDXwpyQngK54cI02GtSxNp7x07kp3zM7O1tzc3KRjSJ2WZL6qZied43SsZamdUerZG8JIktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQeO7PNoiRXAdcBR4CqqjuXbP8UcA7wHHAZcHtVfbfZdgg41Cx9tqquX5PkklbMWpamz9BGnmQ9sBvYUlXHk+xNsr2q9g8sewPwyaqqJB8EfgN4X7NtT1XdsdbBJa2MtSxNpzaH1i8HDlfV8Wb8MHDt4IKq+mxV1cDXfHFg8xVJbk1yV5J3jZxY0mpZy9IUanNo/WzghYHx0WbuFZK8Fvgo8ImB6duq6pFmb+CxJO+tqqdXG1jSqlnL0hRqs0d+BDhrYLyxmXuZpvDvAz5dVQdPzlfVI83fx4DHgW3LvUiSHUnmkswtLCy0/w4ktWUtS1OoTSM/AGxOsq4ZbwP2JdmUZCNAktcD9wP3VNV8kvc389uTXDPwtS4ADrKMqnqgqmaranZmZma134+kU7OWpSk09NB6VR1LcjNwb5IF4Imq2p9kF/A8sBP4PeCtwPlJADYAe1l8t39HkkuBNwJ7q+pbr863Iul0rGVpOuWl81q6Y3Z2tubm5iYdQ+q0JPNVNTvpHKdjLUvtjFLP3hBGkqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx2zkkiT12JltFiW5CrgOOAJUVd25ZPvrgLuBZ4FQJrBjAAAFBklEQVQLgZ1V9WSz7cPAVuAEcLCq7l+7+JJWwlqWps/QRp5kPbAb2FJVx5PsTbK9qvYPLPsV4F+qaleSS4AHgZ9Oci5wC7C1qirJo0keqqqnXo1vRtKpWcvSdGpzaP1y4HBVHW/GDwPXLllzLXAAoKr+CXh7ko3A1cB8VVWz7gDwnpFTS1oNa1maQm0a+dnACwPjo81cmzVtnitpPKxlaQq1+Yz8CHDWwHhjM9dmzRHggiXzTy/3Ikl2ADua4fEk/9wi26T8KPD9SYcYousZu54Pup/xJ1e43lpeXtf/nbueD7qfsev5YOX1/JKqOu0fYD2LBbuuGe8FtgObgI3N3G3Arc3jS4C/bx6fCzwOpBk/ClzY4jXnhq2Z5J+u5+tDxq7n60PGleazlvuZsev5+pCx6/lGzTh0j7yqjiW5Gbg3yQLwRFXtT7ILeB7YCfw2cHeSz7D4rv3jzXO/l+Ru4EtJTgBfKU+OkSbCWpamU6vLz6rqm8A3l8zdOvD4v4BPnOK5XwO+NkJGSWvEWpamT1dvCPPApAMM0fV80P2MXc8H3c/Y9XxgxrXQ9XzQ/YxdzwcjZDz5eZckSeqhru6RS5KkFlp9Rv5qGOVWkR3K+CngHOA54DLg9qr6blfyDay7nsXPNs+qqhfHla957WE/wwC/1Ax/HPjhqvpYxzKez+J/i48C7wB+v6r+fIz5zgE+B7y9qt65zPbXAF8AXgQ2Aw9W1bfHla/J0Ol67nott8k4sM56Xn2+6azlCZ1mv+xlMEvWLHsZTMcy3sVLH098EPiLLuVr5i8GPg8U8IYO/gw/AtwwMH5bBzPeB/xq83gr8NSYM/488D5OcXkK8CHgy83jTcCTwBkd+xlOrJ67XsttMzbz1vNo+aaylid1aH2UW0WOy9CMVfXZan7iLH5MMc53x0PzNffWvhVY9p39GLT5d74e2JTkl5OcfCc6Tm0y/gcw0zyeAebHlA2Aqvo6L7+r2lKDtfI88ANgyxiindT1eu56LYP1PK58U1nLkzq0PsqtIo++utGGvv4rJHkt8FFOcdnOq6RNvs8Dd1XVfy8e8Rq7Nhk3s3gzkl9P8hPAXye5uKpOdCjjPcCfJrkH+CkW9966ZNK3T+16PXe9lsF6Hle+qazlSTXyUW4VOS6tXr8p/PuAT1fVwTFlgyH5kpwH/AjwgYGi/2SSb1TVXBcyNo4C/wBQVU82e2nnAYfGEZB2GfeweAOUP0gyAzyV5M3NO+Yu6EOtTDJj12sZrOdx5dvDFNbypA6tHwA2J1nXjLcB+5JsGjjcto/FQyU0v07xH6tqXHvjrTImeT1wP3BPVc0neX9X8lXVv1bVjVW1s6p2NmvuGWPRD83YzO0H3gzQzJ3B4glHXcp4HvDvzeP/BP6XCV/xkWRD8z8ieHmtbAJeB3xnjHG6Xs9dr+WhGa3nNcs3lbU8sevIk/wMix/8LwD/U1V3nrxVZFXtbArrbhZ/6BcAX6jxn7U+LOOfAG8F/q15yoZa5kzESeVr1swAv8DiIaS7gPur6tmuZEzyQ8Au4DDwFmBvVX1jXPlaZnw3i7+n+zHgfBZ/nefuMea7ErgBuIbFPcbfBD4GXFJVNzVnun4ROAa8CfidGv9Z652u567XcpuMzRrrebR8U1nL3hBGkqQe84YwkiT1mI1ckqQes5FLktRjNnJJknrMRi5JUo/ZyCVJ6jEbuSRJPWYjlySpx/4fQv6hGkTURl8AAAAASUVORK5CYII=\n",
- "text/plain": [
- "<Figure size 576x432 with 6 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "## Example 7\n",
- "## subplot\n",
- "import matplotlib.pyplot as plit\n",
- "import matplotlib.image as mpimg\n",
- "img = mpimg.imread('fig/vis_free_banana.png')\n",
- "\n",
- "fig=plt.figure()\n",
- "fig.set_size_inches(8,6)\n",
- "ax1 = fig.add_subplot(321) \n",
- "ax2 = fig.add_subplot(322)\n",
- "ax3 = fig.add_subplot(323)\n",
- "ax4 = fig.add_subplot(324)\n",
- "ax5 = fig.add_subplot(325)\n",
- "ax6 = fig.add_subplot(326)\n",
- "\n",
- "#ax1.imshow(img); ax2.imshow(img[:,:,0])\n",
- "#ax3.imshow(img[:,:,1]); ax4.imshow(img[:,:,2])\n",
- "#ax5.imshow(img[:,:,3]); ax6.axis('off')\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Adding subplot - Grid control"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 228,
- "metadata": {
- "scrolled": true
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAD7CAYAAABpJS8eAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAFr9JREFUeJzt3X+onnX9x/Hny0mzra06dMT+mFPTmqxl4SkQDf+YQTj6x8IEmQ2DpWQ/+TKFzFhLPaw1UKrN1SAwCrIVGZNgTBghMzonyBJiFnOFtXZkwSbLFfr6/nFf89w7Lu/r3Oe+7vs+5/N6gHBf1/257/vl53M+713357quc2SbiIhY+M4bdICIiOiPFPyIiEKk4EdEFCIFPyKiECn4ERGFSMGPiCjE+Z0aSLoI+AZwle0PnuP584AHgJeAlcBu20/3OmhE9Fbmdnk6FnzgOuAXwPv/x/M3A8tt3yNpBHha0pW2X+lVyIhoROZ2YTou6dj+KXDyDZqsAw5WbY8DLwOre5IuIhqTuV2eOkf4nVzI2T80J6p9ryNpI7ARYOnSpVevWrWqBx8fEZOTky/aHu3x22ZuD6G5jHUvCv4xYFnb9vJq3+vY3gXsAhgbG/PExEQPPj4iJB1p4G0zt4fQXMa6q6t0JC2VdOZfmL3ANdX+EeAC4NluA0XE4GRuL2wdC76k64H1wDsl3SvpzcAGYEvV5CfASUlfA74J3JaTOhHDL3O7PB2XdGwfAA7M2P2dtudfBe7uca6IaFjmdnly41VERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohAp+BERhUjBj4goRAp+REQhUvAjIgqRgh8RUYgU/IiIQqTgR0QUIgU/IqIQKfgREYVIwY+IKEQKfkREIVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiEOfXaSTpBuAm4Bhg25tnPL8BuAN4udq12/ajPcwZEQ3I3C5Lx4IvaQmwE1ht+7SkPZLW2t4/o+kttp9vImRE9F7mdnnqHOFfAxyxfbrafgpYB8z8obhL0lFgCfBt28d7FzMiGpC5XZg6Bf9C4GTb9olqX7sDwF7bU5JuBB4D1vYmYkQ0JHO7MHVO2h4DlrVtL6/2vcb2YdtT1eaTwPWSFs18I0kbJU1Impiampr5dET0V+Z2YeoU/IPASkmLq+1rgb2SRiQtB5D0oKQz3xauAA7bfmXmG9neZXvM9tjo6Ggv8kdE9zK3C9NxScf2KUl3Ag9LmgKesb1f0lbgODAOHAV2SDoMrAHWNxk6IuYuc7s8tS7LtL0P2Ddj36a2xw/1OFdE9EHmdlly41VERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohAp+BERhUjBj4goRAp+REQhUvAjIgqRgh8RUYgU/IiIQqTgR0QUIgU/IqIQKfgREYVIwY+IKEQKfkREIVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGFOL9OI0k3ADcBxwDb3jzj+QuAbcALwBXAuO1DPc4aET2WuV2WjgVf0hJgJ7Da9mlJeySttb2/rdkXgb/a3ippDbAb+HAzkSOiFzK3y1NnSeca4Ijt09X2U8C6GW3WAQcBbP8BuErS8p6ljIgmZG4Xps6SzoXAybbtE9W+Om1OtDeStBHYWG2elvTHWaUdjHcALw46RE3zJWty9t57unhN6XP7jPk0ztDdWAP1Cv4xYFnb9vJq32zbYHsXsAtA0oTtsVmlHYD5khPmT9bk7D1JE128rOi5fcZ8zNvta+ss6RwEVkpaXG1fC+yVNNL21W4vra+HVOt8v7d94vVvFRFDJHO7MB2P8G2fknQn8LCkKeAZ2/slbQWOA+PAQ8A2SfcClwOfbjJ0RMxd5nZ5al2WaXsfsG/Gvk1tj/8NfHaWn71rlu0HZb7khPmTNTl7r6ushc/tM4rJK9u9DBIREUMqd9pGRBSi1pLOXMyXO/lq5LwbuAg4ClwN3Gf7T8OWs63drcAPgWW2X+pjxPYMnfpUwOeqzUuAt9m+va8hqZXzUlo/o78F3g/8yPbjA8h5EfAN4CrbHzzH8+cBDwAvASuB3bafbjDPvJjbbXk65d0A3AG8XO3abfvRvoacztLMWNtu7D9gCfBnYHG1vQdYO6PNPcCm6vEa4NdNZppDzi1ML4F9EvjlMOas9l8J3A8YeEu/c86iT9cDt7Vtv29Ic+4AvlQ9/gDw3ID69BPAx4CJ//H8LcB3q8cjwCFg0QD7beBze5Z5NwCXDCpjP8a66SWd+XInX8ectr/qqndpLYUN4qi5Y87qdvlNwDmP/PuoztjfCoxI+rykM0cr/VYn5z+B0erxKDDZp2xnsf1Tzr4Jaqb2uXSc1pHq6obizJe5fUadvAB3Sfo/SfdJGulfvLM1NdZNL+n07E6+htXJCYCkNwGfYvZXLvRCnZz3A1ts/6e1YjIwdbKuBJbb/rqkdwO/knSl7Vf6FZJ6ObcDP5e0HfgQrW97w6j2z3GfPmsY5nanLO0OAHttT0m6EXgMWNunfLPV1Vg3XfB7didfw2plqIr9DuArtv/Sp2zt3jCnpBXA24Gb24r9lyU9Ybvru/O6VKdPTwC/AbB9qDr6WwE834+AlTo5fwB83/aPJY0Cz0m6rDqyGib9nEvzZW7XzmL7cNvmk8Djkhb1+QCkrq76tuklnflyJ1/HnJLeDDwCbLc9Kenjfc7YMaftv9neYHvc9njVZvsAin3HrNW+/cBlANW+RbROig9bzhXAP6rH/wJeZUiucJO0tPpHCM6eSyPABcCzDX30fJnbZ9SZ4w9KOnMQfAVweJiKfS/GuvHr8CV9hNYJiCngv7Y3n7mTz/Z4VUi30ZpQlwMPeDBX6XTK+TPgvcDfq5cs9TnOng86Z9VmFPgMraWHLcAjtl8YtqyS3gpsBY4A7wL22H5iCHNeR+vXBP8OuBSYtL1zADmvB24DPkrrm+a3gNuBNbbvqK7ceBA4BVwMfM/NXqUzL+b2LPJ+gdYcP0zrJPNDTfZfh6yNjHVuvIqIKESdP4AyVNf+RrMy3hELV52TttcBv6B1w8m53EzrSot7qrWkpwdwpUX0TsY7YoHqeOJpyK79jYZlvCMWrl5cljmba9hf+6s4S5cuvXrVqlU9+Pg4l8nJyRdtj3ZuOWsZ74gBmsvc7kXBr309qNv+Ks7Y2JgnJgZxtWAZJB1p6K0z3hEDNJe53dW1xAO89jcGIOMdsTB0LPjV9aDrgXdKure6tnYD07eX/wQ4KelrwDdp/TKsnMCbpzLeEQtXnT9xeIDW75ho9522518F7u5xrhiQjHfEwjUUt4dHRETzUvAjIgqRgh8RUYgU/IiIQqTgR0QUIgU/IqIQKfgREYVIwY+IKEQKfkREIVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGFSMGPiChECn5ERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohDn12kk6QbgJuAYYNubZzy/AbgDeLnatdv2oz3MGX2SsY5YuDoWfElLgJ3AatunJe2RtNb2/hlNb7H9fBMhoz8y1hELW50j/GuAI7ZPV9tPAeuAmUXgLklHgSXAt20f713M6JOMdcQCVqfgXwicbNs+Ue1rdwDYa3tK0o3AY8DamW8kaSOwEeDiiy/uKnA0qmdjDRnviGFT56TtMWBZ2/byat9rbB+2PVVtPglcL2nRzDeyvcv2mO2x0dHRbjNHc3o21lXbjHfEEKlT8A8CKyUtrravBfZKGpG0HEDSg5LOfFu4Ajhs+5Xex42GZawjFrCOSzq2T0m6E3hY0hTwjO39krYCx4Fx4CiwQ9JhYA2wvsnQ0YyMdcTCVuuyTNv7gH0z9m1qe/xQj3PFgGSsIxau3HgVEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGFSMGPiChECn5ERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohAp+BERhUjBj4goRAp+REQhUvAjIgqRgh8RUYgU/IiIQqTgR0QUIgU/IqIQKfgREYVIwY+IKMT5dRpJugG4CTgG2PbmGc9fAGwDXgCuAMZtH+px1uiDjHXEwtWx4EtaAuwEVts+LWmPpLW297c1+yLwV9tbJa0BdgMfbiZyNCVjHbGw1VnSuQY4Yvt0tf0UsG5Gm3XAQQDbfwCukrS8ZymjXzLWEQtYnSWdC4GTbdsnqn112pxobyRpI7Cx2jwt6Y+zSjtY7wBeHHSIWXhPF6/p2VjDvB3v+TLOydl78yVrN3MbqFfwjwHL2raXV/tm2wbbu4BdAJImbI/NKu0Azce8XbysZ2MN83O8k7O35ktOmD9Zu5zbQL0lnYPASkmLq+1rgb2SRtq+yu+ltRxAta77e9uvO+KLoZexjljAOh7h2z4l6U7gYUlTwDO290vaChwHxoGHgG2S7gUuBz7dZOhoRsY6YmGrdVmm7X3Avhn7NrU9/jfw2Vl+9q5Zth+0IvI2NNZd5xmA5Oyt+ZIT5k/WrnPKdi+DRETEkMqdthERhUjBj4goRK01/LmYb7fq18i7AbgDeLnatdv2o30NeXaei4BvAFfZ/uA5nj8PeAB4CVhJK+/TDWWZN2NdI+vdwEXAUeBq4D7bfxq2nG3tbgV+CCyz/VIfI575/E79KeBz1eYlwNts397XkNTKeSmtn9HfAu8HfmT78QHkbGZe227sP2AJ8GdgcbW9B1g7o809wKbq8Rrg101m6kHeDcAlg8p4jsyfAD4GTPyP528Bvls9HgEOAYtKHuuaWbcwfY7rk8AvhzFntf9K4H7AwFuGMSewHritbft9Q5pzB/Cl6vEHgOf6nbP67EbmddNLOvPtVv06eQHukvR/ku6TNNK/eK9n+6ecfefrTO39e5zWN5PVDUSZT2PdMavtr7qaTbSWPvt+1EyNnNXvP9oEnPPIv0/qjP2twIikz0s6c2Tab3Vy/hMYrR6PApN9ynaWpuZ100s6Pb1Vvw/q5D0A7LU9JelG4DFgbZ/ydaPO/1O/PmdYxrp2n0h6E/ApursUda7q5Lwf2GL7P61Vk4Gok3MlsNz21yW9G/iVpCttv9KvkNTLuR34uaTtwIdofdMbRl3N66YLfk9v1e+DjllsH27bfBJ4XNKiPv/gzka/+nc+jXWtHFWx3wF8xfZf+pSt3RvmlLQCeDtwc1ux/7KkJ2x3fft9F+r05wngNwC2D1Xf7FYAz/cjYKVOzh8A37f9Y0mjwHOSLquOoodJV3Op6SWd+Xarfse8kh6UdOYfyiuAw8NW7CUtrX5Y4ez+HQEuAJ5t4GPn01jXGec3A48A221PSvr4sOW0/TfbG2yP2x6v2mzvc7HvmLPatx+4DKDat4jWCfFhy7kC+Ef1+F/AqwzJ1Yy9mNeN33gl6SO0TkBMAf+1vfnMrfq2x6uJtY1WJ18OPODBXqXTKe8XgPcCh2mdeHzIDV31UjPv9cBtwEdpHY1+C7gdWGP7jups/oPAKeBi4HtN5Z1PY10j689ojfPfq5cs9Tmulhh0zqrNKPAZWssPW4BHbL8wTDklvRXYChwB3gXssf1EPzPWzHkdrb/58DvgUmDS9s4B5GxkXncs+MN02V9ERHSvzhr+dcAvaF2Tei430zoZc0/11eLpAZyMiYiIDjquTQ3RZX8RETEHvbhKZzaXuL32F5CWLl169apVq3rw8RER5ZicnHzR9mjnlq/Xi4Lf1V9AGhsb88REvy8miIiY3yQd6fa1XV1uNKDL/iIiYg46Fvzq8qD1wDsl3VtdWreB6TvQfgKclPQ14Ju0fl9GTthGRAyZOn/i8ACtXyfQ7jttz78K3N3jXBER0WNDcQdZREQ0LwU/IqIQKfgREYVIwY+IKEQKfkREIVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGFSMGPiChECn5ERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohAp+BERhUjBj4goRAp+REQhUvAjIgpxfp1Gkm4AbgKOAba9ecbzG4A7gJerXbttP9rDnBERMUcdC76kJcBOYLXt05L2SFpre/+MprfYfr6JkBERMXd1jvCvAY7YPl1tPwWsA2YW/LskHQWWAN+2fbx3MSMiYq7qFPwLgZNt2yeqfe0OAHttT0m6EXgMWNubiBER0Qt1TtoeA5a1bS+v9r3G9mHbU9Xmk8D1khbNfCNJGyVNSJqYmpqa+XRERDSoTsE/CKyUtLjavhbYK2lE0nIASQ9KOvNt4QrgsO1XZr6R7V22x2yPjY6O9iJ/RETU1HFJx/YpSXcCD0uaAp6xvV/SVuA4MA4cBXZIOgysAdY3GToiImav1mWZtvcB+2bs29T2+KEe54qIiB7LjVcREYVIwY+IKEQKfkREIVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGFSMGPiChECn5ERCFS8CMiCpGCHxFRiBT8iIhCpOBHRBQiBT8iohAp+BERhUjBj4goRAp+REQhUvAjIgqRgh8RUYgU/IiIQqTgR0QU4vw6jSTdANwEHANse/OM5y8AtgEvAFcA47YP9ThrRETMQceCL2kJsBNYbfu0pD2S1tre39bsi8BfbW+VtAbYDXy4mcgREdGNOks61wBHbJ+utp8C1s1osw44CGD7D8BVkpb3LGVERMxZnSWdC4GTbdsnqn112pxobyRpI7Cx2jwt6Y+zSrtwvQN4cdAhhkT6Ylr6Ylr6Ytp7un1hnYJ/DFjWtr282jfbNtjeBewCkDRhe2xWaReo9MW09MW09MW09MU0SRPdvrbOks5BYKWkxdX2tcBeSSNtyzZ7aS39UK3h/972ide/VUREDErHI3zbpyTdCTwsaQp4xvZ+SVuB48A48BCwTdK9wOXAp5sMHRERs1frskzb+4B9M/Ztanv8b+Czs/zsXbNsv5ClL6alL6alL6alL6Z13Rey3csgERExpHKnbUREIWot6cxF7tKdVqMv7gYuAo4CVwP32f5T34P2Qae+aGt3K/BDYJntl/oYsW9q/FwI+Fy1eQnwNtu39zVkn9Toi0tp1YvfAu8HfmT78b4HbZiki4BvAFfZ/uA5nj8PeAB4CVgJ7Lb9dMc3tt3Yf8AS4M/A4mp7D7B2Rpt7gE3V4zXAr5vMNKj/avbFFqaX2T4J/HLQuQfVF9X+K4H7AQNvGXTuAf5crAdua9t+36BzD7AvdgBfqh5/AHhu0Lkb6otPAB8DJv7H87cA360ejwCHgEWd3rfpJZ3cpTutY1/Y/qqrEaS13LYgj2ip0RfVr/TYBJzzyH8BqTNHbgVGJH1e0pmjuoWoTl/8ExitHo8Ck33K1le2f8rZN7PO1F43jwMvA6s7vW/TSzo9u0t3AajTFwBIehPwKWZ/5dN8Uacv7ge22P5Pa0VjwarTFyuB5ba/LundwK8kXWn7lX6F7JM6fbEd+Lmk7cCHaH0rLlHtetKu6YLfs7t0F4Ba/59Vsd8BfMX2X/qUrd/esC8krQDeDtzcVuy/LOkJ213fZTik6vxcnAB+A2D7UPUNeAXwfD8C9lGdvvgB8H3bP5Y0Cjwn6bLqKLckXdXNppd0cpfutI59IenNwCPAdtuTkj4+oKxNe8O+sP032xtsj9ser9psX4DFHurNkf3AZQDVvkW0TuwvNHX6YgXwj+rxv4BXKeRqQ0lLq3/k4Oy6OQJcADzb8T2ml4ybIekjtE5ATAH/tb35zF26tserIreN1iBeDjzghXuVTqe++BnwXuDv1UuW+hxn6BeCTn1RtRkFPkPra/sW4BHbLwwqc1Nq/Fy8FdgKHAHeBeyx/cTgEjenRl9cR+vXsf8OuBSYtL1zcImbIel64Dbgo7S+8X8LuB1YY/uO6iqdB4FTwMXA91zjKp3ceBURUYgivgpFREQKfkREMVLwIyIKkYIfEVGIFPyIiEKk4EdEFCIFPyKiECn4ERGF+H83cEm/MIentwAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 432x288 with 5 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "### Example 8\n",
- "## grid control A\n",
- "import matplotlib\n",
- "\n",
- "img = mpimg.imread('fig/vis_free_banana.png')\n",
- "\n",
- "grid = plt.GridSpec(3, 3, wspace=0.4, hspace=0.3)\n",
- "\n",
- "ax1 = plt.subplot(grid[0, 0:2])\n",
- "ax2 = plt.subplot(grid[0, 2])\n",
- "ax3 = plt.subplot(grid[1, 0])\n",
- "ax4 = plt.subplot(grid[1, 1:3]);\n",
- "ax5 = plt.subplot(grid[2, 0:3]);\n",
- "\n",
- "#ax1.imshow(img, aspect='auto'); ax2.imshow(img[:,:,0], aspect='auto') \n",
- "#ax3.imshow(img[:,:,1], aspect='auto'); ax4.imshow(img[:,:,2], aspect='auto')\n",
- "#ax5.imshow(img[:,:,3], aspect='auto')\n",
- "plt.show()\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Adding subplot - Controlling the grid"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 229,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAssAAAHUCAYAAADMYGUIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAHktJREFUeJzt3X+opXd9J/D3xwSjiZnVoTdYShxj2602/sTbljQt/SNZWAgubFx0Ia2KhXHTomj+GINGbTZR0+imNFCNs0ql9MeuNFvqkiIM84dsQpTOLDRtQXSFTaWrzpXYTkLquNbP/pET93gzX+8zd8655yT39YLA+T7nO899O843zztnvs9zqrsDAAA81bNWHQAAANaVsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAMX7jShql6Y5PYkr+runzvL+89K8qEkjyU5lORT3f2FRQcFds86BoDd2bEsJ/mlJH+e5NWD99+Q5EB331xVB5N8oape1t3/vKiQwHmzjgFgF3bchtHdf5rk0R8x5bokD87mPpLkO0muXEg6YCGsYwDYnSmfLO/ksvzwRfj07NhTVNXhJIeT5JJLLnntS1/60gX8eFhfJ0+e/FZ3b6w6xwTWMQw8jdbxZNYx+835rONFlOVTSS6dGx+YHXuK7j6a5GiSbG5u9okTJxbw42F9VdXDq84wkXUMA0+jdTyZdcx+cz7reFdPw6iqS6rqyXZ+X5KrZscPJnlOkr/dbSBgb1jHALCzHctyVf1Kkl9L8uNVdUtVPTfJW5LcNpvymSSPVtUHknwkyZvcFATrxToGgN3ZcRtGd38+yee3Hf69ufe/n+TdC84FLJB1DAC740tJAABgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAICBC6dMqqprk1yf5FSS7u5bt71/RZKPJvnLJK9O8sfd/dkFZwUAgD21Y1muqouT3JPkyu4+U1X3VtU13X18btqRJPd39+9U1WuSfCaJsgwAwNPalG0YVyV5uLvPzMYPJLlu25xvJtmYvd5IcvJsJ6qqw1V1oqpObG1t7SYvAHCeXI9huill+bIkj86NT8+OzbsryS9U1V1J3p/k9892ou4+2t2b3b25sbFxtikAwJK5HsN0U/Ysn0py6dz4wOzYvE8n+WR3/0lVbST5SlW9pLsfWUxMAADYe1M+WX4wyaGqumg2vjrJfVV1sKoOzI5dnuTrs9ffTvL9iecGAIC1teMny939eFXdmOTuqtpK8lB3H6+qO5M8kuSOJO9K8s6q+sUkVyR5T3d/a5nBAQBg2SY9Oq67jyU5tu3YkbnX9ye5f7HRAABgtWyVAACAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAgQunTKqqa5Ncn+RUku7uW7e9X0nePhu+OMnzu/utC8wJAAB7bseyXFUXJ7knyZXdfaaq7q2qa7r7+Ny0X03yD939B7Nf88rlxAUAgL0zZRvGVUke7u4zs/EDSa7bNueGJAer6h1V9aEkjy0wIwAArMSUsnxZkkfnxqdnx+YdSnKgu+9O8ukkn6uqC7afqKoOV9WJqjqxtbW1y8gAwPlwPYbpppTlU0kunRsfmB2bdzrJF5Oku788m3P59hN199Hu3uzuzY2Njd0lBnalqq6tqo9V1W9V1QfO8v4Vs21WN1fVf6mqf7OKnMDyuR7DdFNu8HswyaGqumi2FePqJB+rqoNJvtfdp5McT/KSJKmqA0kuSPKNJWUGztHEew+OJLm/u3+nql6T5DNJPruKvACwLnYsy939eFXdmOTuqtpK8lB3H6+qO5M8kuSOJL+d5M6qek+Sn0zy5u7+zjKDA+dkdO/BfFn+ZpInP2LaSHJy7+IBwHqa9Oi47j6W5Ni2Y0fmXv9jkrctNhqwQFPuPbgryZ9V1V1Jfj7JbWc7UVUdTnI4SV70ohctPikArJFJZRl42pty78Gnk3yyu/+kqjaSfKWqXtLdj8xP6u6jSY4myebmZi8vMgCsnm/wg/3hB/cezMZXJ7mvqg7O7jNInrgp9+uz199O8v34dwQA+5xPlmEfmHjvwbuSvLOqfjHJFUne093fWl1qAFg9ZRn2iQn3Htyf5P69zgUA68xfsQIAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwMCFUyZV1bVJrk9yKkl3962DeTck+cMkl3b3YwtLCQAAK7BjWa6qi5Pck+TK7j5TVfdW1TXdfXzbvJcl+dkl5QQAgD03ZRvGVUke7u4zs/EDSa6bnzAr1EeSnPUTZwAAeDqaUpYvS/Lo3Pj07Ni8Dya5rbu/+6NOVFWHq+pEVZ3Y2to6t6QAwEK4HsN0U8ryqSSXzo0PzI4lSarq8iQvSPKGqrp5dvimqtrcfqLuPtrdm929ubGxcR6xAYDdcj2G6abc4PdgkkNVddFsK8bVST5WVQeTfK+7v5bkLU9OrqoPJ7nLDX4AADzd7fjJcnc/nuTGJHdX1e1JHprd3Hdzkt94cl5VbVTVLbPhkar6iWUEBgCAvTLp0XHdfSzJsW3HjmwbbyW5ffYPAAA87flSEgAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBgQFkGAIABZRkAAAaUZQAAGFCWAQBg4MIpk6rq2iTXJzmVpLv71m3vvzvJC5N8I8lrk7y/u7+04KwAALCndizLVXVxknuSXNndZ6rq3qq6pruPz017XpKburur6o1JPpLkdcuJDAAAe2PKNoyrkjzc3Wdm4weSXDc/obvf1909d87HFhcRAABWY0pZvizJo3Pj07NjT1FVz07y5iS3DN4/XFUnqurE1tbWuWYFABbA9Rimm1KWTyW5dG58YHbsh8yK8seTvLe7v3q2E3X30e7e7O7NjY2N3eQFAM6T6zFMN6UsP5jkUFVdNBtfneS+qjpYVQeSpKqem+QTSe7q7pNV9frlxAUAgL2z4w1+3f14Vd2Y5O6q2kryUHcfr6o7kzyS5I4kf5Tk5UmuqKokuSTJvcuLDQAAyzfp0XHdfSzJsW3Hjsy9vn7BuQAAYOUmlWXg6W/C89IrydtnwxcneX53v3VPQwLAmlGWYR+Y+Lz0X03yD939B7Nf88pVZAWAdeLrrmF/2PF56UluSHKwqt5RVR+K56UDgLIM+8SU56UfSnKgu+9O8ukkn6uqC7afyPNZAdhPlGXYH6Y8L/10ki8mSXd/eTbn8u0n8nxWAPYTZRn2hx2fl57keJKXJMns2AVJvrHnSQFgjbjBD/aBic9L/+0kd1bVe5L8ZJI3d/d3VpcaAFZPWYZ9YsLz0v8xydv2OhcArDPbMAAAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYEBZBgCAAWUZAAAGlGUAABhQlgEAYODCKZOq6tok1yc5laS7+9Zt7z8nyUeT/H2Sn05yR3d/ecFZAQBgT+1Ylqvq4iT3JLmyu89U1b1VdU13H5+b9s4kf9fdd1bVK5J8KskvLycyAADsjSnbMK5K8nB3n5mNH0hy3bY51yV5MEm6+6+TvKqqDiwsJQAArMCUbRiXJXl0bnx6dmzKnNPzk6rqcJLDs+GZqvqbc0q7fD+W5FurDnEW65hLpml+ZtUBALZzPd4VmaZbx1y7vh5PKcunklw6Nz4wO3auc9LdR5McTZKqOtHdm+eUdsnWMVOynrlkmqaqTqw6A8B2rsfnTqbp1jHX+VyPp2zDeDDJoaq6aDa+Osl9VXVwbqvFfXliu0Zme5b/qrtPP/VUAADw9LHjJ8vd/XhV3Zjk7qraSvJQdx+vqjuTPJLkjiS/m+SjVXVLkp9K8uvLDA0AAHth0qPjuvtYkmPbjh2Ze/1PSX7zHH/20XOcvxfWMVOynrlkmmYdMwHMW8d/T8k0zTpmStYz164zVXcvMgiwj2xubvaJE7Zl88xWVSfXbf8lsHd8gx8AAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADF+40oapemOT2JK/q7p87y/vPSvKhJI8lOZTkU939hUUHBQCAvbZjWU7yS0n+PMmrB++/IcmB7r65qg4m+UJVvay7/3lRIQEAYBV23IbR3X+a5NEfMeW6JA/O5j6S5DtJrlxIOgAAWKEpnyzv5LL8cJk+PTv2FFV1OMnhJLnkkkte+9KXvnQBPx7W18mTJ7/V3RurzgEwz/WY/eZ8rseLKMunklw6Nz4wO/YU3X00ydEk2dzc7BMnTizgx8P6qqqHV50BYDvXY/ab87ke7+ppGFV1SVU92c7vS3LV7PjBJM9J8re7DQQAAOtix7JcVb+S5NeS/HhV3VJVz03yliS3zaZ8JsmjVfWBJB9J8iY39wEA8Eyw4zaM7v58ks9vO/x7c+9/P8m7F5wLAABWzpeSAADAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAgLIMAAADyjIAAAwoywAAMKAsAwDAwIWrDgDsjaq6Nsn1SU4l6e6+dTDvhiR/mOTS7n5sDyMCwNpRlmEfqKqLk9yT5MruPlNV91bVNd19fNu8lyX52ZWEBIA1ZBsG7A9XJXm4u8/Mxg8kuW5+wqxQH0ly1k+cAWA/UpZhf7gsyaNz49OzY/M+mOS27v7ujzpRVR2uqhNVdWJra2vBMQFgvSjLsD+cSnLp3PjA7FiSpKouT/KCJG+oqptnh2+qqs3tJ+ruo9292d2bGxsby8wMACtnzzLsDw8mOVRVF822Ylyd5GNVdTDJ97r7a0ne8uTkqvpwkrvc4AfAfueTZdgHuvvxJDcmubuqbk/y0OzmvpuT/MaT86pqo6pumQ2PVNVP7H1aAFgfPlmGfaK7jyU5tu3YkW3jrSS3z/4BgH1vUlne6fmsVXVFko8m+cskr07yx9392QVnBQCAPbVjWZ74fNYjSe7v7t+pqtck+UwSZRkAgKe1KXuWd3w+a5JvJnnytviNJCcXEw8AAFZnSlme8nzWu5L8QlXdleT9SX7/bCfyfFYAWD3XY5huSln+kc9nnfl0kk92901J/m2S/zp7JNUP8XxWAFg912OYbkpZ/sHzWWfjq5PcV1UHq+rA7NjlSb4+e/3tJN+feG4AAFhbO97g192PV9WTz2fdyuz5rFV1Z5JHktyR5F1J3llVv5jkiiTv6e5vLTM4AAAs26RHx+30fNbuvj/J/YuNBgAAq2WrBAAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwcOGUSVV1bZLrk5xK0t1967b3K8nbZ8MXJ3l+d791gTkBAGDP7ViWq+riJPckubK7z1TVvVV1TXcfn5v2q0n+obv/YPZrXrmcuAAAsHembMO4KsnD3X1mNn4gyXXb5tyQ5GBVvaOqPpTksQVmBACAlZhSli9L8ujc+PTs2LxDSQ50991JPp3kc1V1wfYTVdXhqjpRVSe2trZ2GRkAOB+uxzDdlLJ8Ksmlc+MDs2PzTif5YpJ095dncy7ffqLuPtrdm929ubGxsbvEAMB5cT2G6aaU5QeTHKqqi2bjq5PcV1UHq+rA7NjxJC9JktmxC5J8Y9FhAQBgL+14g193P15VNya5u6q2kjzU3cer6s4kjyS5I8lvJ7mzqt6T5CeTvLm7v7PM4AAAsGyTHh3X3ceSHNt27Mjc639M8rbFRgMAgNXypSQAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADCgLAMAwICyDAAAA8oyAAAMKMsAADBw4aoDAHujqq5Ncn2SU0m6u2/d9v67k7wwyTeSvDbJ+7v7S3seFADWiLIM+0BVXZzkniRXdveZqrq3qq7p7uNz056X5Kbu7qp6Y5KPJHndKvICwLqwDQP2h6uSPNzdZ2bjB5JcNz+hu9/X3T0bPivJY3uYDwDWkrIM+8NlSR6dG5+eHXuKqnp2kjcnuWXw/uGqOlFVJ7a2thYeFADWyaSyXFXXVtXHquq3quoDP2LeDVXVVfW8xUUEFuBUkkvnxgdmx37IrCh/PMl7u/urZztRdx/t7s3u3tzY2FhKWABYFzuW5bm9ju/q7t9K8sqquuYs816W5GcXnhBYhAeTHKqqi2bjq5PcV1UHq+pAklTVc5N8Isld3X2yql6/oqwAsDam3OA32uv4gxuDZoX6SJK3JXnPokMC56e7H6+qG5PcXVVbSR7q7uNVdWeSR5LckeSPkrw8yRVVlSSXJLl3VZkBYB1MKctT9jp+MMlt3f3d2UX2rKrqcJLDSfKiF73o3JIC56W7jyU5tu3YkbnX1+95KGAlXI9huil7ln/kXsequjzJC5K8oapunh2+qao2t5/IXkcAWD3XY5huyifLP9jrONuKcXWSj1XVwSTf6+6vJXnLk5Or6sN5Ys+jx04BAPC0tuMny939eJIn9zrentlexyQ3J/mNJ+dV1UZVPfmoqSNV9RPLCAwAAHtl0jf47bTXcTbeSnL77B8AAHja86UkAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMCAsgwAAAPKMgAADCjLAAAwoCwDAMDAhVMmVdW1Sa5PcipJd/et295/d5IXJvlGktcmeX93f2nBWQEAYE/tWJar6uIk9yS5srvPVNW9VXVNdx+fm/a8JDd1d1fVG5N8JMnrlhMZAAD2xpRtGFclebi7z8zGDyS5bn5Cd7+vu3vunI+d7URVdbiqTlTVia2trd1mBgDOg+sxTDelLF+W5NG58enZsaeoqmcneXOSW872fncf7e7N7t7c2Ng416wAwAK4HsN0U8ryqSSXzo0PzI79kFlR/niS93b3VxcTDwAAVmdKWX4wyaGqumg2vjrJfVV1sKoOJElVPTfJJ5Lc1d0nq+r1y4kLAAB7Z8cb/Lr78aq6McndVbWV5KHuPl5VdyZ5JMkdSf4oycuTXFFVSXJJknuXFxsAAJZv0qPjuvtYkmPbjh2Ze339gnMBAMDK+VISAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAYuHDKpKq6Nsn1SU4l6e6+ddv7z0ny0SR/n+Snk9zR3V9ecFbgPFjHAHDudizLVXVxknuSXNndZ6rq3qq6pruPz017Z5K/6+47q+oVST6V5JeXExk4V9YxAOzOlG0YVyV5uLvPzMYPJLlu25zrkjyYJN3910leVVUHFpYSOF/WMQDswpRtGJcleXRufHp2bMqc0/OTqupwksOz4Zmq+ptzSrt8P5bkW6sOcRbrmEumaX5m1QFmrOPVWsdMyXrmWsdM67KOF8Y63hWZplvHXLtex1PK8qkkl86ND8yOneucdPfRJEeTpKpOdPfmOaVdsnXMlKxnLpmmqaoTq84wYx2v0DpmStYz17pmWnWGRbOOz51M061jrvNZx1O2YTyY5FBVXTQbX53kvqo6OPdXtPflib/mzWyv41919+mnngpYEesYAHZhx0+Wu/vxqroxyd1VtZXkoe4+XlV3JnkkyR1JfjfJR6vqliQ/leTXlxkaODfWMQDszqRHx3X3sSTHth07Mvf6n5L85jn+7KPnOH8vrGOmZD1zyTTN2mSyjldqHTMl65lLpr23jv/7ZJpmHTMl65lr15mquxcZBAAAnjF8gx8AAAwoywAAMDBpz/L5WMev2J2Q6d1JXpjkG0lem+T93f2lVWaam3dDkj9Mcml3P7bMTFNyVVUlefts+OIkz+/ut6440xV54s/UXyZ5dZI/7u7PLjHPC5PcnuRV3f1zZ3n/WUk+lOSxJIeSfKq7v7CsPMtgHS8m09y8PVvH1vDkTM/odbyOa3hiLut4Qibr+Ac/cznruLuX9k+Si5P8ryQXzcb3Jrlm25ybkxyZvX5Fkv+xBpluy//fz/3GJP991Zlmx1+W5INJOsnzlpnpHH6vfi3Jm+bGr1yDTB9P8q7Z69ck+cqSM/27JK9LcmLw/r9P8rHZ64NJvpzkgmX//7fHv+fW8RquY2v4nHI9Y9fxOq7hc8hlHVvH55JrKet42dsw1vErdnfM1N3v69nvZJ7YqrLsT3B3zFRVFyc5kuSs/4W7qlxJbkhysKreUVVP/tfaqjN9M8nG7PVGkpPLDNTdf5of/ua77eb/jD+S5DtJrlxmpgWzjheUaQXr2Bqe6Bm+jtdxDU/KZR1PyxTrOMny1vGyt2Es7Ct29zhTkqSqnp3kzTn3x2ktI9MHk9zW3d994m9b9sSUXIeSHOju/1hV/zLJ56rqZd39zyvMdFeSP6uqu5L8fJ74ZGKVJv+ZW1PW8eIy7fU6toYX5+m8jtdxDU/NlcQ6npDJOp5mV+t42WV5YV+xu8eZnlyYH0/y3u7+6hLz7Jipqi5P8oIkb5hbmDdV1V909zK/hnXK79XpJF9Mku7+8uyTiMuT/O8VZvp0kk92959U1UaSr1TVS2b/FbkKe/1nfNGs4wVkWtE6toYX5+m8jtdxDU/+mdaxdbxAu/pzvuxtGOv4Fbs7Zqqq5yb5RJK7uvtkVb1+iXl2zNTdX+vut3T3Hd19x2zOXUsuyjvmmh07nuQlSTI7dkGeuBFjlZkuT/L12etvJ/l+9vjJL1V1yexfDskP/xk/mOQ5Sf52L/OcJ+t4AZlWtI6t4fPwDFrH67iGJ+WyjnfONDtmHQ8sYh0v/UtJqupf5YkN11tJ/m9331qzr9jt7jtmC+GjeeI39KeSfKiXfxf9Tpn+W5KXJ/k/s19ySZ/lrsq9zDSbs5HkbXnirzJuS/KJ7v77Veaqqn+R5M4kDyf5yST3dvdfrDjTLyV5Z5L/meSKJCe7+54l5vmVJG9K8q/zxKcf/ynJW5O8orv/Qz1x9+2Hkzye5EVJ/nM/je6iT6zjRWWazdnTdWwNT870jF7H67iGJ+ayjidkso5/kGkp69g3+AEAwIAvJQEAgAFlGQAABpRlAAAYUJYBAGBAWQYAgAFlGQAABpRlAAAY+H+JEYF/Uiyu5gAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 864x576 with 5 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "### Example 9\n",
- "### Grid control B\n",
- "import matplotlib\n",
- "import matplotlib.image as mpimg\n",
- "img = mpimg.imread('fig/vis_free_banana.png')\n",
- "\n",
- "plt.figure(figsize=(12,8))\n",
- "grid = plt.GridSpec(2, 3, wspace=0.3, hspace=0.1) \n",
- "\n",
- "ax1 = plt.subplot(grid[0, 0],); plt.setp(ax1.get_xticklabels(), visible=False)\n",
- "ax2 = plt.subplot(grid[0, 2]); plt.setp(ax2.get_yticklabels(), visible=False); plt.setp(ax2.get_xticklabels(), visible=False)\n",
- "ax3 = plt.subplot(grid[1, 0])\n",
- "ax4 = plt.subplot(grid[1, 2]); plt.setp(ax4.get_yticklabels(), visible=False)\n",
- "ax5 = plt.subplot(grid[0:2, 1])\n",
- "\n",
- "#ax1.imshow(img); ax2.imshow(img[:,:,0])\n",
- "#ax3.imshow(img[:,:,1]); ax4.imshow(img[:,:,2])\n",
- "#ax5.imshow(img[:,:,3])\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Adding subplot - Fine arragement"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 244,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZgAAAHUCAYAAAAHoT5CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3X+o3nd99/Hny4rRxJxp2CkdI8ZWt7WLbZUeN7o4HKSDQfCPO4466LSlg7huKNob0lJrd2e1NYtdZIG1aaasiD+4ZdmYoyJ3OH/IWqJ4Mlg3QdoJy8RZc0rckpJ5nOv7/uP6Rq+cnuS6TnJ9rutK8nzAge/nc33O9X1zcn3y+v6+UlVIkjRqr5h0AZKkS5MBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCZeOWhAkquAjwE3VtXbV3j9FcDDwIvAJuDTVfW1URcqTRPnhTTYwIAB3gH8LfDWs7x+KzBTVfcm2QB8Lcl1VfU/oypSmkLOC2mAgYfIquqvgJPnGLINONyNPQ78ENg8kuqkKeW8kAYbZg9mkCs5c6Kd6PpeJskOYAfAunXrbrr22mtHsHrpwh05cuSFqpod4Vs6L3RJuJC5MYqAOQas72vPdH0vU1UHgAMAc3NztbCwMILVSxcuydERv6XzQpeEC5kb53UVWZJ1SU4n2pPAzV3/BuDVwDfPtyDpYuW8kM40MGCSvBN4L/BzSe5P8hrgDuDBbsgXgZNJ/gj4BPA+T2TqUue8kAYbeIisqr4KfHVZ95/3vf4ScM+I65KmmvNCGswbLSVJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTRgwkqQmBn5lMkCSW4DtwDGgqmrXstevBh4BvgG8Ffh8VX1pxLVKU8V5IZ3bwIBJshbYD2yuqqUkB5Nsrar5vmE7gaeq6pNJ3gZ8EXAi6ZLlvJAGG+YQ2c3A0apa6tpPA9uWjfk+MNstzwJHVnqjJDuSLCRZWFxcPJ96pWkxsnkhXaqGCZgrgZN97RNdX7+9wK8m2Qs8APzlSm9UVQeqaq6q5mZnZ1caIl0sRjYv3PDSpWqYczDHgPV97Zmur98TwKeq6gtJZoHnklxTVcdHU6Y0dUY2L6rqAHAAYG5urtqVLI3XMHswh4FNSdZ07S3Ak0k2JJnp+jYC3+uWfwC8NOR7Sxcr54U0wMA9mKo6leQuYF+SReCZqppPsgc4DuwGPgx8KMmvAVcD91XVCy0LlybJeSENNtRlylV1CDi0rG9n3/JTwFOjLU2abs4L6dzcXZckNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNTHUN1omuQXYDhwDqqp2LXs9wAe65huB11XVnSOsU5o6zgvp3AYGTJK1wH5gc1UtJTmYZGtVzfcN+13gP6rqM93v3NCmXGk6OC+kwYY5RHYzcLSqlrr208C2ZWNuAzYk+WCSh4EXR1ijNI2cF9IAwwTMlcDJvvaJrq/fJmCmqvYBTwBfSXLF8jdKsiPJQpKFxcXF8yxZmgrOC2mAYQLmGLC+rz3T9fU7AXwdoKqe7cZsXP5GVXWgquaqam52dvb8Kpamg/NCGmCYgDkMbEqypmtvAZ5MsiHJTNc3D1wD0PVdATw/6mKlKeK8kAYYeJK/qk4luQvYl2QReKaq5pPsAY4Du4E/AfYkuQ94E3B7Vf2wZeHSJDkvpMGGuky5qg4Bh5b17exb/k/g/aMtTZpuzgvp3LzRUpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUxFDfaJnkFmA7cAyoqtp1lnG3AZ8F1lfViyOrUpJ00RkYMEnWAvuBzVW1lORgkq1VNb9s3HXALzeqU5o6bnhJ5zbMIbKbgaNVtdS1nwa29Q/oQmgnsOIEky41fRteH66q/wPckGTrCuPc8NJla5iAuRI42dc+0fX1ewh4sKp+dK43SrIjyUKShcXFxdVVKk0XN7ykAYYJmGPA+r72TNcHQJKNwOuBW5Pc23XfnWRu+RtV1YGqmququdnZ2QsoW5o4N7ykAYY5yX8Y2JRkTbe1tgV4NMkG4MdV9R3gjtODk3wc2OuxZl3iVrPhdbr77iRfrqqF/jeqqgPAAYC5ublqWbQ0TgMDpqpOJbkL2JdkEXimquaT7AGOA7sBkswC7+9+bWeSx6vqu60KlybMDS9pgKEuU66qQ8ChZX07l7UXgY91P9IlzQ0vabChAkbSy7nhJZ2bd/JLkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpoY6hstk9wCbAeOAVVVu5a9fg9wFfA8cBPwQFV9a8S1SpIuIgMDJslaYD+wuaqWkhxMsrWq5vuGvRa4u6oqyXuATwDvalOyNB3c8JLObZg9mJuBo1W11LWfBrYBPwmYqvpo3/hXAC+u9EZJdgA7AN7whjecT73SVHDDSxpsmHMwVwIn+9onur6XSfIq4Hbg/pVer6oDVTVXVXOzs7OrrVWaJmfb8PqJqvpoVVXXPOeGV5KFJAuLi4vNCpbGbZiAOQas72vPdH1n6MLlMeAjVfXt0ZQnTS03vKQBhgmYw8CmJGu69hbgySQbkswAJHkN8Diwt6qOJHl3m3KlqeGGlzTAwHMwVXUqyV3AviSLwDNVNZ9kD3Ac2A18DngLcHUSgHXAwXZlSxP3kw2v7jDZFuDRJBuAH1fViW7D61Hgkar6ZpJ3V5XzQpeNoS5TrqpDwKFlfTv7lrePuC5pqrnhJQ02VMBIejk3vKRz805+SVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJob6wrEktwDb6X3neFXVrmWvvxp4BPgu8AvA7qp6dsS1SpIuIgMDJslaYD+wuaqWkhxMsrWq5vuGfQj4t6rak+R64NPAr7cpWZoObnhJ5zbMIbKbgaNVtdS1nwa2LRuzDTgMUFX/BNyYZGZkVUpTpm/D68NV9X+AG5JsXTbs9IbXx4FP0tvwki4bwxwiuxI42dc+0fUNM+ZE/6AkO4AdXXMpyT+vqtrR+1nghcu8hkmvf1pq+KVVjj/bhlf/nv024D7obXgluTHJTFWdQLoMDBMwx4D1fe2Zrm+1Y6iqA8ABgCQLVTW3qmpHzBomv/5pqmGVv+KGlzVcLjWsduPrJ4YJmMPApiRruq21LcCjSTYAP+62xp6kt0X39905mH90K02XODe8rOGyqeF8f3fgOZiqOgXcBexL8jHgme4E/73AH3TD/oxeCN0P/G/g9863IOki8ZMNr669BXgyyYa+84+nN7xww0uXo6EuU66qQ8ChZX07+5b/C/jDVa77wCrHt2ANk18/XIQ1VNWpJKc3vBbpNryS7AGOA7vpbXg90m14vRk3vHSZSVVNugZJnSQ7ukNm1mANF30NBowkqYmhDpFdiGm4GW2IGu4BrgKeB24CHqiqb41r/X3jbgM+C6yvqhdHtf5hakgS4ANd843A66rqzjHXcDW9z8I3gLcCn6+qL41w/VcBHwNurKq3r/D6K4CHgReBTcCnq+pro1q/dNmpqmY/wFrgX4A1XfsgsHXZmHuBnd3y9cDfT6CGB/np3tx7gL8b5/q7/uuAh4ACXjuBv8F7gff1tW+YQA2P0btxEeBtwHMjruG3gXcBC2d5/XeAR7vlDcCzwBWjrMEffy6nn9Z7MNNwM9rAGqrqo33jX0FvC3ZUBq6/uyt8J/B+ur/FiA3z73Ab8JUkH6S3N/epCdTwfWC2W54FjoyygKr6qyS/cY4h24D/1409nuSHwGbgmVHWAe7ZD1tD3zj37i/CvfvWATOym9Ea1wBAklcBt7P6K+IudP0PAQ9W1Y96n+WRG6aGTcBMVf1xkl+kFzbXVdX/jLGGvcDfJNkL/Aq9PctxGvqzciGm4fl+Q9bwWuDuqqok7wE+QW8PcJw1kOQ64JdHtd7zqOF3gf+oqs90v3PDBGrYCTxVVZ9M8jbgi8DIAgZ4B/C39MJrJbfS+//h3u4eyK8N8/9D68f1j+xmtMY1nA6Xx4CPVNW3x7X+JBuB1wO3Jrm36747yShvrhrmb3AC+DpAt6U8A2wccw1PAJ+qqruB/wX83+7DPC6tP4unTcPz/QbWUFUfrarTVwGNes9+qBr69u5X3LMZRw309u43JPlgktNb8eOuofnePWduXC3X/3k8Dpzeuz+n1gEzDTejDawhyWuAx4G9VXUkybvHtf6q+k5V3VFVu6tqdzdmb1Wd992zq62h65sHrgHo+q6gd2hknDVsBL7XLf8AeInGn9Ek65Kcnrj9n8UNwKuBbzZY7YXs2Y+zBuCMPfv7R7j+YWv4yd79iNe9mhpO793vo7cR9JUkV4y5hr3Ar3Z79w8AfznC9Q/jvD6PTQ+R1RTcjDZkDZ8D3gJc3R2iWkfvJPS41k/3n9z7u1/bmeTxqvruGGv4E2BPkvuANwG3V9UPR7H+VdTwYeBDSX4NuBq4r6pG9hymJO+kdzHDz3Wftz8F7qB3ccnv0zvs8LYkfwS8gd5FD6M6RNjPPfshali2d3+6++4kXx7hBtiq9+67DaKNwL+OsYYn6O3df6H7v+K5JNd0exPjcH6fx0lfZeCPP5fbD2e5oo7elWszXd9Erq5cVsNr6G0pb+7a7x53DcvGj+0Ky2V/h4eBu7rlGWARePWYa/gG8Bvd8ivpbZT97Ij/Fr9B3xWW9Da0Z7vl87rC0hstpQlI8pv0LpteBP67qnad3purqt3dYdtH6B0yfDPwcI3+KrJBNfw1vT37f+9+ZV2tcIVRyxq6Maf37h/sfka2dz9MDUl+BtgDHKW3d3+wqr48qvUPWcM76F348Q/09u6PVNX+Ea7/ncD7gN+it8f6p8CdwPVV9fvdVWQfB07R27v/ixriKjIDRpLUROuT/JKky5QBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwMfFdPqMc7Sxcx5IQ02zLPImjzGWbrIOS+kAQYGTI3wS5qS7AB2AKxbt+6ma6+99nxqlpo4cuTIC1U1O3ik80KXj9XMi+VG8TTloR/jXFUHgAMAc3NztbAwyifSSxcmydERvp3zQpeEC5kXozjJP64vaZIuJs4LXfbOK2Am9CVN0lRzXkhnGhgwy7+kqXuM+B389PvSvwic7L6k6RO0+5ImaWo4L6TBhjnJ/1Xgq8u6/7zv9ZeAe0ZclzTVnBfSYN5oKUlqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqYuA3WgIkuQXYDhwDqqp2LXv9auAR4BvAW4HPV9WXRlyrNFWcF9K5DQyYJGuB/cDmqlpKcjDJ1qqa7xu2E3iqqj6Z5G30vo/ciaRLlvNCGmyYQ2Q3A0eraqlrPw1sWzbm+8BstzwLHBlNedLUcl5IAwwTMFcCJ/vaJ7q+fnuBX02yF3gA+MuV3ijJjiQLSRYWFxfPp15pWjgvpAGGOQdzDFjf157p+vo9AXyqqr6QZBZ4Lsk1VXW8f1BVHQAOAMzNzdV5Vy1NnvNCGmCYPZjDwKYka7r2FuDJJBuSzHR9G4Hvdcs/AF4a8r2li5XzQhpg4B5MVZ1KchewL8ki8ExVzSfZAxwHdgMfBj6U5NeAq4H7quqFloVLk+S8kAYb6jLlqjoEHFrWt7Nv+SngqdGWJk0354V0bu6uS5KaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0M9ZXJSW4BtgPHgKqqXcteD/CBrvlG4HVVdecI65SmjvNCOreBAZNkLbAf2FxVS0kOJtlaVfN9w34X+I+q+kz3Oze0KVeaDs4LabBhDpHdDBytqqWu/TSwbdmY24ANST6Y5GHgxRHWKE0j54U0wDABcyVwsq99ouvrtwmYqap9wBPAV5JcsfyNkuxIspBkYXFx8TxLlqaC80IaYJiAOQas72vPdH39TgBfB6iqZ7sxG5e/UVUdqKq5qpqbnZ09v4ql6eC8kAYYJmAOA5uSrOnaW4Ank2xIMtP1zQPXAHR9VwDPj7pYaYo4L6QBBp7kr6pTSe4C9iVZBJ6pqvkke4DjwG7gT4A9Se4D3gTcXlU/bFm4NEnOC2mwoS5TrqpDwKFlfTv7lv8TeP9oS5Omm/NCOjdvtJQkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNTHUN1omuQXYDhwDqqp2nWXcbcBngfVV9eLIqpSmkPNCOreBAZNkLbAf2FxVS0kOJtlaVfPLxl0H/HKjOqWp4ryQBhvmENnNwNGqWuraTwPb+gd0k20nsOIWnHQJcl5IAwwTMFcCJ/vaJ7q+fg8BD1bVj871Rkl2JFlIsrC4uLi6SqXp4ryQBhgmYI4B6/vaM10fAEk2Aq8Hbk1yb9d9d5K55W9UVQeqaq6q5mZnZy+gbGninBfSAMOc5D8MbEqypjscsAV4NMkG4MdV9R3gjtODk3wc2OvJTF3inBfSAAP3YKrqFHAXsC/Jx4BnuhOZ9wJ/cHpcktkk93fNnUl+vkXB0jRwXkiDpaomsuK5ublaWFiYyLqllSQ5UlUvO4Q1Ts4LTZsLmRfeaClJasKAkSQ1YcBIkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ18cphBiW5BdgOHAOqqnYte/0e4CrgeeAm4IGq+taIa5WmivNCOreBAZNkLbAf2FxVS0kOJtlaVfN9w14L3F1VleQ9wCeAd7UpWZo854U02DCHyG4GjlbVUtd+GtjWP6CqPlpV1feeL46uRGkqOS+kAYYJmCuBk33tE13fyyR5FXA7cP9ZXt+RZCHJwuLi4mprlaaJ80IaYJiAOQas72vPdH1n6CbRY8BHqurbK71RVR2oqrmqmpudnT2feqVp4byQBhgmYA4Dm5Ks6dpbgCeTbEgyA5DkNcDjwN6qOpLk3W3KlaaG80IaYOBJ/qo6leQuYF+SReCZqppPsgc4DuwGPge8Bbg6CcA64GC7sqXJcl5Igw11mXJVHQIOLevb2be8fcR1SVPPeSGdmzdaSpKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0M9ZXJSW4BtgPHgKqqXctefzXwCPBd4BeA3VX17IhrlaaK80I6t4EBk2QtsB/YXFVLSQ4m2VpV833DPgT8W1XtSXI98Gng19uULE2e80IabJg9mJuBo1W11LWfBrYB/RNpG3AfQFX9U5Ibk8xU1Yn+N0qyA9jRNZeS/PMFVX/hfhZ4wRqsofNLqxjrvLCGy6WG1cyLMwwTMFcCJ/vaJ7q+YcacMZGq6gBwACDJQlXNrbbgUbIGa1hewyqGOy+s4bKp4Xx/d5iT/MeA9X3tma5vtWOkS4nzQhpgmIA5DGxKsqZrbwGeTLIhyUzX9yS9QwZ0x5r/cflhAOkS47yQBhh4iKyqTiW5C9iXZBF4pqrmk+wBjgO7gT8DHklyP/Bm4PeGWPeBC6h7VKyhxxp6hq7BedGcNfRc1DWkqkZZiCRJgDdaSpIaMWAkSU0MdSf/hZiGu52HqOEe4CrgeeAm4IGq+tY4a+gbdxvwWWB9Vb04zhqSBPhA13wj8LqqunPMNVxN7/PwDeCtwOer6ksjXP9VwMeAG6vq7Su8/grgYeBFYBPw6ar62qjW37ce58UQNfSNc15cjPOiqpr9AGuBfwHWdO2DwNZlY+4FdnbL1wN/P4EaHuSn56PeA/zduGvo+q8DHgIKeO0E/g7vBd7X175hAjU8Bny4W34b8NyIa/ht4F3Awlle/x3g0W55A/AscMUE/g7Oi5+Oc15cpPOi9SGys93t3G8bvUs+qap/Am7su8xzLDVU1Uer+8vRO2w40i2kYWroHj2yE1hxC24cNQC3ARuSfDDJ6a2VcdfwfWC2W54FjoyygKr6K868+XG5/s/jceCHwOZR1oDzYuganBc/cVHOi9aHyEZ2t3PjGgBI8irgduAPR7Tu1dTwEPBgVf2ot0c+csPUsAmYqao/TvKLwFeSXFdV/zPGGvYCf5NkL/Ar9Laix2noz0vjdTgvepwXPRflvGgdMNNwt/NQ799NoseAj1TVt0e4/oE1JNkIvB64tW8S3Z3ky1V13o9pWE0NnRPA1wGq6tlui3kj8K9jrOEJ4FNV9YUks8BzSa7ptprGYRx33zsvhqjBeXGGJ7gI50XrQ2TTcLfzwBqSvAZ4HNhbVUeSvHuE6x9YQ1V9p6ruqKrdVbW7G7N3hJNoYA1d3zxwDUDXdwW9E7zjrGEj8L1u+QfASzT+nCZZ101aOPPzuAF4NfDNEa/SeTFEDc6Li39eNL/RMslv0juBtAj8d1XtOn23c1Xt7j7Ej9D7470ZeLhGf7XMoBr+GngL8O/dr6yrFa6kaFlDN2YWeD+93d8Hgcer6rvjqiHJzwB7gKPAm4CDVfXlUa1/yBreQe8x9/8AXA0cqar9I1z/O4H3Ab9Fb8v8T4E7geur6ve7q2U+DpwC3gD8RbW5isx5MUQN3RjnxUU6L7yTX5LUhDdaSpKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWqi+eP6tXrNHp0tSWNkwEyndwB/S+97H1ZyK72H793bPbbhayN++J4kXTAPkU2hKXmkvCRdEPdgLk6redT6DmAHwLp162669tpr21cnNXLkyJEXqmp28EhNAwPm4jT0o7Or6gBwAGBubq4WFkb5IFppvJIcnXQNGp6HyC4SE3ikvCRdEANmCnWPzn4v8HNJ7u8e3X4HP/0Wuy8CJ5P8EfAJet8X7gl+SVPFQ2RTqKq+Cnx1Wfef973+EnDPWIuSpFVyD0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwq9MnlJJbgG2A8eAqqpdy16/GngE+AbwVuDzVfWlsRcqSWdhwEyhJGuB/cDmqlpKcjDJ1qqa7xu2E3iqqj6Z5G3AFwEDRtLU8BDZdLoZOFpVS137aWDbsjHfB2a75VngyEpvlGRHkoUkC4uLi02KlaSVGDDT6UrgZF/7RNfXby/wq0n2Ag8Af7nSG1XVgaqaq6q52dnZlYZIUhMeIptOx4D1fe2Zrq/fE8CnquoLSWaB55JcU1XHx1SjJJ2TezDT6TCwKcmarr0FeDLJhiQzXd9G4Hvd8g+Al/DfU9IUcQ9mClXVqSR3AfuSLALPVNV8kj3AcWA38GHgQ0l+DbgauK+qXphc1ZJ0JgNmSlXVIeDQsr6dfctPAU+Nuy5JGpaHVCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTRgwkqQmDBhJUhMGjCSpCQNGktSEASNJasKAkSQ1YcBIkpowYCRJTfiNllMqyS3AduAYUFW1a9nrAT7QNd8IvK6q7hxrkZJ0DgbMFEqyFtgPbK6qpSQHk2ytqvm+Yb8L/EdVfab7nRsmUasknY2HyKbTzcDRqlrq2k8D25aNuQ3YkOSDSR4GXhxngZI0iAEzna4ETva1T3R9/TYBM1W1D3gC+EqSK5a/UZIdSRaSLCwuLraqV5JexoCZTseA9X3tma6v3wng6wBV9Ww3ZuPyN6qqA1U1V1Vzs7OzjcqVpJczYKbTYWBTkjVdewvwZJINSWa6vnngGoCu7wrg+bFXKkln4Un+KVRVp5LcBexLsgg8U1XzSfYAx4HdwJ8Ae5LcB7wJuL2qfji5qiXpTAbMlKqqQ8ChZX07+5b/E3j/uOuSpGF5iEyS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwq9MnkJJbgG2A8eAqqpdZxl3G/BZYH1VvTjGEiVpIANmyiRZC+wHNlfVUpKDSbZW1fyycdcBvzyRIiVpCB4imz43A0eraqlrPw1s6x/QhdBOYMU9G0maBgbM9LkSONnXPtH19XsIeLCqfjTozZLsSLKQZGFxcXGEZUrSuRkw0+cYsL6vPdP1AZBkI/B64NYk93bddyeZW+nNqupAVc1V1dzs7GyrmiXpZTwHM30OA5uSrOkOk20BHk2yAfhxVX0HuOP04CQfB/Z6kl/StHEPZspU1SngLmBfko8Bz3Qn+O8F/uD0uCSzSe7vmjuT/Pz4q5Wks0tVTboGjcnc3FwtLCxMugzpvCU5UlUrHg7W9HEPRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUhAEjSWrCgJEkNWHASJKaMGAkSU0YMJKkJgwYSVITBowkqQkDRpLUxCsnXYBWluQWYDtwDKiq2rXs9XuAq4DngZuAB6rqW2MvVJLOwoCZQknWAvuBzVW1lORgkq1VNd837LXA3VVVSd4DfAJ41yTqlaSVeIhsOt0MHK1GJbmjAAAFNElEQVSqpa79NLCtf0BVfbSqqmu+AnhxjPVJ0kAGzHS6EjjZ1z7R9b1MklcBtwP3n+X1HUkWkiwsLi6OvFBJOhsDZjodA9b3tWe6vjN04fIY8JGq+vZKb1RVB6pqrqrmZmdnmxQrSSsxYKbTYWBTkjVdewvwZJINSWYAkrwGeBzYW1VHkrx7QrVK0oo8yT+FqupUkruAfUkWgWeqaj7JHuA4sBv4HPAW4OokAOuAg5OqWZKWM2CmVFUdAg4t69vZt7x97EVJ0ip4iEyS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCYMGElSEwaMJKkJA0aS1IQBI0lqwq9MnlJJbgG2A8eAqqpdy15/NfAI8F3gF4DdVfXs2AuVpLMwYKZQkrXAfmBzVS0lOZhka1XN9w37EPBvVbUnyfXAp4Ffn0S9krQSD5FNp5uBo1W11LWfBrYtG7MNOAxQVf8E3JhkZnwlStK5uQczna4ETva1T3R9w4w50T8oyQ5gR9dcSvLPoy31vP0s8MKki+gzTfVMUy0wXfX80qQL0PAMmOl0DFjf157p+lY7hqo6ABwASLJQVXOjLfX8TFMtMF31TFMtMF31JFmYdA0anofIptNhYFOSNV17C/Bkkg19h8GepHcoje4czD9W1YmXv5UkTYZ7MFOoqk4luQvYl2QReKaq5pPsAY4Du4E/Ax5Jcj/wZuD3JlexJL2cATOlquoQcGhZ386+5f8C/nCVb3tgBKWNyjTVAtNVzzTVAtNVzzTVogFSVZOuQZJ0CfIcjCSpCQNGktSE52AuMdP2iJkh6rkHuAp4HrgJeKCqvjWJWvrG3QZ8FlhfVS+2qGWYepIE+EDXfCPwuqq6c0K1XE3vc/MN4K3A56vqSy1q6dZ3FfAx4MaqevsKr78CeBh4EdgEfLqqvtaqHp2nqvLnEvkB1gL/Aqzp2geBrcvG3Avs7JavB/5+wvU8yE/PBb4H+LtJ1dL1Xwc8BBTw2gn/bd4LvK+vfcMEa3kM+HC3/DbguVZ/m24dvw28C1g4y+u/AzzaLW8AngWuaFmTP6v/8RDZpWXaHjEzsJ6q+mh1/0vQO2Tbao9hYC3dM+B2Aivu2Yy7HuA2YEOSDyY5vbU+qVq+D8x2y7PAkUa1AFBVf8WZT6pYrv9zfBz4IbC5ZU1aPQ+RXVpG9oiZMdYDQJJXAbez+kuvR1nLQ8CDVfWj3tGppoapZxMwU1V/nOQXga8kua6q/mcCtewF/ibJXuBX6O15TtLQny1NjgFzaRnZI2bGWM/pcHkM+EhVfXsStSTZCLweuLUvXO5O8uWqavF4kmH+NieArwNU1bPdnuZG4F8nUMsTwKeq6gtJZoHnklzT7T1Mwjg/xzpPHiK7tEzbI2YG1pPkNcDjwN6qOpLk3ZOopaq+U1V3VNXuqtrdjdnbKFwG1tP1zQPXAHR9V9C7GGIStWwEvtct/wB4iTH//5FkXRducObneAPwauCb46xHg3mj5SUmyW/SO0G6CPx3Ve06/YiZqtrd/Yf+CL3/LN4MPFxtryIbVM9fA28B/r37lXW1wlVD46ilGzMLvJ/eIaAHgcer6ruTqCfJzwB7gKPAm4CDVfXlCdXyDnrfQfQPwNXAkara36KWrp53Au8Dfove3u2fAncC11fV73dXkX0cOAW8AfiL8iqyqWPASJKa8BCZJKkJA0aS1IQBI0lqwoCRJDVhwEiSmjBgJElNGDCSpCb+P4bzk8SxRIrXAAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 468x576 with 5 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "## Example 10\n",
- "## Fine arragement\n",
- "from matplotlib import pyplot as plt\n",
- "from mpl_toolkits.mplot3d import axes3d\n",
- "img = plt.imread('fig/vis_free_banana.png')\n",
- "\n",
- "fig = plt.figure(figsize=(6.5,8))\n",
- "\n",
- "# add low level axes: x , y , xsize, ysize\n",
- "ax1 = fig.add_axes([0.125, 0.66, 0.35, 0.22]) ## from bottom, left.\n",
- "# normal way\n",
- "ax2 = fig.add_subplot(322)\n",
- "ax3 = fig.add_subplot(323)\n",
- "ax4 = fig.add_subplot(324)\n",
- "# new subdivision\n",
- "ax5 = plt.subplot2grid((3,8),(2,2),colspan=4)\n",
- "\n",
- "#ax1.imshow(img); ax2.imshow(img[:,:,0])\n",
- "#ax3.imshow(img[:,:,1]); ax4.imshow(img[:,:,2])\n",
- "#ax5.imshow(img[:,:,3]); \n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Spectrogram multiplot"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 209,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAtgAAAEHCAYAAACUUzFiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsvXnQJdlZ3vl7T253+favlq5udXVrA7EGRmLfBAgHBkQYxsiDDUjjhYEhzMxgQMNqgdkMZmAMgYEwIMOMbbCBwJZYJSQhQSMhBUIIkNDWUlerumv9trvkcs47f7wn837dqmpVo+ou0X2eiBv33ry5nMw8mffN5zzv84qqkpCQkJCQkJCQkJBwc+BudQMSEhISEhISEhISnkhIAXZCQkJCQkJCQkLCTUQKsBMSEhISEhISEhJuIlKAnZCQkJCQkJCQkHATkQLshISEhISEhISEhJuIFGAnJCQkJCQkJCQk3ESkADvhpkJEvkBE3iwiKiKvEZE/EJF3iMgvicj0VrfvRiAi3yEiD4jIS45Ne4uIPOMmb+emr/Ma2/hSEXmbiLz6sdxOQkLCkwsicpeI/Ea8x79SRF4tIt9wq9uVkPDhAkk+2Ak3GyLyXOBVQKGqnYhsA28D/r2qvuRWtu1GISIvBe7t2ysiW6q6d5O3cdPXeZ3tvAh4kao+97HeVkJCwpMDIvIq4L+q6k/F788FfkJVP+4x3q4CT1XVex/L7SQkfKhIDHbCYw5VvQq8FnjOrW7L3xSPRSD8eATXCQkJCY8RPhl4df9FVV8N/H+3qjEJCR9uSAF2wuOFHDjXfxGR7xKRe0Tk90XkZSJye5z+fSLSicgbROQOEVkTkUMR2RCRTEReLyL3isgHsCQi8mUi8loReVUctvyMOP3zjssk4nz3Rpa6X/bpcdl7ROQXgPGx335URPYiE9xP+xoR+eO4nV8VkdPX2mkROS0ivxXb9DoRefEjrPPbReQvROR3ReTFUWbzahE5G7elIvJCEXmFiLxdRD792LJfKyJ/FI/nK0Xkox/tCUpISEh4FHgv8K3HpX+q+kMw3I/uFZFfE5H/FO+rrxWRp/bzisiz4/3zNfGe9axjvz093jdfE5d9SZz+W3GW/xLvjXfFdxWRb4jLLEXkuSKyLiI/F++794jIt4qIxPVkIvLjIvLnIvLbIvKSuNyvicgni8kc7xWRb4n3VY3LXe9/q5fivUZEflhE3iQivxPv3b8Uf/v+x/h8JHy4QVXTK71u6gt4LqBAHr+fBX4DuOPYPP+ClUTpRcAvHfvtdcBXxs9/H+iA/yl+f0H/+Rrb/SpgJ36+G3jfsd9eBLz62PeXAC899v31wLfFz3cAV4CXHPv91ZjMAuAzgQvAyfj9O4FXXqdNPwy8OH6eAq+7zjq/CDh/rP0/apfnMO/d8Zi+IH7/VuB3jv3+vwLVseP/2uvte3qlV3ql14f6Aj4fuAzsAb8AfM7Dfn9J/O1M/P7twB/Fz5vAReDz4vcvBt6OkX4Z8JfAC4/Ne+7YehW4+2HbUuC74+d/BHwi8HP9PR4jTN4CfHX8/r8BfwaMAAH+KyYJ7Nf3XKABnhe//9v4/kj/Wy8CjrD/OwH+FHg5UAKngLo/Fun15HglBjvhscQrReTPMP3176nq/cd+uw94lYj8AfB/AM8+9tvLgC+Jn/8udqP8omPff/c62/sz4BdE5HXAS4E7ReTUB2ukiNyFDXf+vwCxna97hEVeCLxMVS/G778AfJ6InL3GvFeAvyciH6Oqs9j+a+ErgN9U1Svx+/WGWn87vr8FeOqx6X8J/A8ReS3wQzz0eCYkJCTcVKjqK7Fg8psxAuBVIvIzD5vtNap6Pn7+JeDT4n3yS4AjVf39uK6XA7cBnwJ8KvAM4j1QVfeBf3gDTfqNOP9/At4M/GPg5+O0BfDLwP8S5/0K4L+p6lJVFfjP11jfTFVfEZf/5jjtkf63AN6uqu+L6/wL4G2q2qjqBeyB4qkkPGmQAuyExxKfD/wd4CeBH+mDXRF5JvArwLeo6mdjN6rJseVeDnyhiOTAFnZj/nsikgFTVT28zvb+O8bcfqauEvom15n3OM7E90vHpl251owRT8Fulj0uHpv+cPwI8KvAL4vImzGm5npt+KDbV9WD+HGJMSOIyCb2UPKzqvpZwP/MMYlLQkJCwmMBVZ2p6n9Q1c8FPhf4ZyLy9GOzXD32+XJ8P4PdK3eivOPVUb53EdiNv11V1e7Ydv7wBpqzf+zzSaDiA+/T/T36Ru63x9d3I/9bAMf/m7prfC8feRcSnkhIAXbCYwpVDdhQ4SEmYwALug9U9U/i9+Jhy/w5NtT2dRgTcQ92s/x6TMrxAYjB+91EhldEiofN0sR19Ng69rlnWE4em7b7CLt138Pm7T+fu8a8p1T1J1T1YzGm55ce9gd0vA03uv2H4yOBDVbs9sP3PSEhIeGmQkT+/fHvqvoaLIjeODZ559jnE/H9PHYPPaeqz+1fmKzjd+NvW5Fg6bf1USLyaEiDi5gk4+H36f4e/Te53z7i/1ZCwsORAuyExxyqOgf+H+DrY+D7TmBbRD4izvKF11js5cD3YlIMjwWP3xunXwu9FvBTrrPO9wDPFJFKREYY29K3773AG4CvBhCRO4DPeYRdeinwRSLS/2G8EPh9VX3fNeb9QRH5hPj59VigL9eY71fiOvsb/QseYfsPx3sxduR6+56QkJBws/E8Efnk/ouIfA6mhX7bsXk+XUT6EcKvAe6J98mXAbsi8klx2Slm7bqJ3SffhWmpEZEd7P7YM9pHwEREvkpE/sG1GhaJnV/EdNHE4PwFmJyPuL5/ICKjmPj4FTewvzfyv5WQsMKtFoGn1xPrBXwBxjor8Brgo+P0TWzI7Y1YkuC/Bu7FdHM/g0kefvHYer4IeNex7/8I07c90rb/PvBu4HeA749t+GNWiYO/BLwV01r/BPAA8B3xt6djuus/xvR4vxbb97VYwuEe9sfxxXH+r4rz/kGc9/R12vTFcZ7fB94EfGOcfq11fjumpf5t4BuJSY4YC/THcX9+A9M9vvn4McPY/nuxP64fi/P+LvClcRt7mEftLe8j6ZVe6fW3/wX883iPf1W8x70a+NRjv78E0z2/FBuFfC3wtGO/Pzsu85q4/Jcc++3pwG/F317LsQRKLMfkLfF+fVu8z/X3+s87Nt8a8B+O3ddfzCpBMcdIn7cCvwn8X8B74m8ffez++ur+/yP+ds3/LeDzjt1nvyf+bzwQ5/0y4KfivG8m/iem1xP/lQrNJCR8GCAOh040aqwjs/MyVb2m/V9CQkLChzOitd7dqvqiW9yUD0AcxXRqo6uIyFcA36yqn/LISyYk3DiSRCQh4cMDd2OMSI+vwpj4hISEhISbi88EvgtARBw2Qprutwk3FSnATkj48MAloIpFDe7Bsty/6Ra3KSEhIeFRQ0S+FtM/f6GIfMctbs618E7g2dFu7x6srsEP3tomJTzRkCQiCQkJCU9yiMjzgC/HAg1V1e+5xjwvwIKQ/11VX/Zolk1ISEh4siH/4LMkJCQkJDxRISIT4KeBj1HVWkR+VUQ+X62QSD/PUzHrs/se7bIJCQkJT0b8rQ+wT5w4oXffffetbkZCQkLC3whvetObLqnqyQ8+52OGTwPeq6p1/P6HmPvNECSr6nuA94jIv3q0y8IgGfhaACnKZ1c7pxAPea10Y0E6CAUUs0Cz7hAPzmPeEGLvziu+ElRsmmtsmX4eCeA6CBloDuJtelYrmgm+gHyphEIIObgWQm7L5TNPu54hutokar+F/l9SIWuUkAuagwrky/i7QLHX4icFfgSa2e+ujW3rVvtBbD/B3lXsOIRCCM62qQ5cv20FUXCNggi+ivvGat9cp7QTwXlblmPth9ieft3RJFTUPktYtWuYJ4vT4nyutXlDAflcadcE19l82VLxIxnW4bq4aFx3KGxfRVff+/b3+5+1EJwt6/ZntKemZA34KrZDMUGrQlbb9P7Y9ufHtfYe8tWhLmaBbupWxzqL83bxOPXrBkJp57Or7Pce3tIhbb4giEJxZH2xP6/9+Ra1c62Z7WO/r5ofO/axP4QyHtd4zIn9xTUBXzk0t/Pry9Wx7furxmOlYuvp+/rQ3zz4cjXPYAwbf5Ng14kE63sKdBMZrrtQHOv7sf/ZQWLo+3Ygj30+3pcUdBSgc6u+qKBlQGo3HIPj++H86lrq97E/N8O+AflBQ7tVDv2878f9SR++a7yfbLih76FxvfLQPtNfH1ltx60/H7Hp5LXimkCzmYHC8sFzN3TPvikBtoh8C5akdQl4JvBPsUpyP4TZpj0T+HZVffDY/BvANvC7qvrf4/RPAL4B8yw+hWX1djwC7r77bt74xjfejN1ISEhIeNwhIu+9xU04xUMrzh3EaTdtWVX9WeBnAca33alPe+E3UV1Rtt5dc+njRoyuBBYnHafeuOD+zx5TzKDaU1xnAW1WK+VRYP/unFBYgLVxb2B+mwO1P+Z8DpOLnnrDUe8K+cz+NLfe3dKsZxze6dj9y5bZ6Zz5aWF6XlmcEPIFnH79Ae//nA1cEwMeteAmX8D8lAVV4mHz3o75bsbilKAOdt7mmZ3OwMHtLzvHwSeeYe8ZGfWOEgples7hKxhdskDJAnQIhZDPFc2hGwtb7+yYn8po1oViprRToTxU5qeFrLZAYOO+jpAJVz8io7qqiMLGezuajYzxhYYLzx5RXbXgtw8m8rlFKN1U6CaQLWPASwzuMntQyZYWMIbKlmk2xYLi+NAyPe8JuTC/zXHiLTXnP7VifEmpt4Wdv+q48qzcHm5yGF9U1Nm68znM7hCyha2nmCnz24TigOFBoxvB+rlAvSFMLgam/+NNnP/Hn8za/YG9pzuyJgarJRBg692eg7syxhcDKsLilEVCkwcCCCx2LaBSB6ffMOPCs6fkS8UXQrNp+z550I6xBHCtIh4Onwq7b1X2numoYl1H8creRyk67aBxZAtHthTO/GHH/tMKqj1rQ71tDz75AqqrgXbNzuP8lKM8tOOUxYcxX8H4gnJ0VhhfsO/WF4TpA57puQUHT52wOOnYfE/H0e3ZEBguTgn5HPwYRhftnM3vUPKZgMDoos1X7SmHZ4XRZXv46QNzX9lvxQyWO0JxaNdgyITLH1eRz5Tx5cDR7RnFTFmctGOUxcfnfKEsd219moGvrA+HXNFCyY/s4TirhfojFuiVKh5HyJZCuGtJ/q4RoYTRReuT1WU7t9VVW7evoDyEbsIQrIcSpu9XVODU772P888/Ozzkibe2dCN7QJLOHgJQOP36Gec+3x7W8rlN6yarB6K1c4pm0K4J7RpsvjtwcNZRzOyBtz/u2+9sGb/3kPc9f4eshr/40W+6oXv2hxxgi8htwLcBJ1Q1iMhvYHq8zwJeoaq/IiLPB/4t8NUi8inA56rqF8WiI38ZEw32MX/i56nqAyLyo1gBj5/7UNuYkJCQkHBdXADWj33fiNMek2V7Zmr6oOf+zxqRNTAvHNLBpY8fD6xoyCKjOILFSUdxZH+C5aH9gS53HN0oMk+N/Wke3JXhPGQLC5C7sXD1mQXd2Biy+cmcZsOChnrLmGiAC59ku+Bapd2If6wiFow6cEsLUK48KyefxR0R2HtGRrlvwduDz7tjYA79yAIOggUA7dSC9LYSmg0ojiC0tn/Nhq03q22d9bYFjO1UjOXswGew3MwsyBTwlR0LdTkqwtGZEZrZstJFgjy3gMx1FnT0gUgoIJ8dYzJLC/hD0QceMrDCfYC93HYD43/pYytwsX05LLczsgZcDT7Wx9WMODJhwXYo7Xwsd2X4XsyUZt3ad3jWETIIecbVf/nJbL7bs9xxA4vYrts59WM4OJvhSzv/7TSOdACLUw5X23pdC/PbhHxvgeZT6i1h8qDag9fc2FqwgLPZsM8ht1EAFWg27cGjmwpaeWtHGQhecLVw+WMLXAuzM25gu0NuwVvIHONLgdkdjmwJszNCMbNtWUBPZKctYA2loE7oxjA7lXF45xpgLPmVj8wpD5TlCRlY/HpHCaUFgPWZFjfLWG525Hs59Y5QHFkfRKDZsge0UMDoil0PfmRBbCig3RAufeyI9fu9nZdcOLg7s4fA0pbtxivW15d2/noWWzPwk4DmCkWgA3TskTLS9U6pLmYUMzh8ekcG1Kc8buHsQTCOXHUTcK21ywJ3Y9jLfeimq9Gmekc4/yVnmd1hD4uusWOfLRUVe2hdnBDWzimz24Vzn2fBNRqv7TUZRr0kQLMu+NHqAeLojDNWPrPp+czadvUjCq5+xA6hWrHeN4Kb4SIyx6rT9eVR14C/wIYJ74nT+mFDgC/pp6tqC/wV8NnA04Cxqj5wjWUSEhISEh4b3APcJSJV/P4ZwMtFZEdENh5huesu+4hLRBnBwV05oTCGNRRxaDeLAWUlLE4L85MW2EkwBkozqLfsD9+P4tB1DMImFwPdxAICP7IAMJ8bQ1UcwYm3tCxOWNBqwcZqaL2XjXQTMYlJtmJ6Qwb1tgX6IbPgK1+upAp+ZA1YnBK6sVBdBc0VdUo3sbZ3U1juWkCgme2zr4RmQyj3bb6sUfK5RrbPgph8bn/o1VVjvn0hTB5Q/NhkFctdwXkFZ+2TDspDpTxQk8csobqiuM4+Nxu2TguqjaHtH1JClNVIlOb0bGtWK82GBRz9kH1xZPskAQ7P2jHLF/bj4qRY4FLB8qQdG/Gr/RiG/QO0Gw8dpm827dztPSOjG8vAihNsvwapjUA7tQcrgr26kQVDi5MyMK/ve/4Jmk3bv3rTmPTxRaVZX0lh8sXqQaLZWElf/MiCbsAkImARk4NmQweJhXTW50Stf7TrFnijq4eYXpqC2nGvtyxg9iUDGyze9l98PDZTodmy0QQ/su27xh7eXCs0uwFyC25lbAGya+24tOsm99DYL5DVQ4XEY6qOYaTh6jMzXGsPMD72jf5BuO8rvQSm36/iEEKhSCOMHshxlUcLRXJFW0fx3gotlOaZCw6f3kGmhCvlcBwkQDFfHZd6ezWqIt7Ox/hysH5YwvKE0I1WD9Pi7Vz4kV1L3dgeSnBwdFaGfuKaeG43LbgOBYR4t6p37L3ZiNdmZL67cexT49W+9zKp/oHuRvAhM9iqehAlH78sIueBc5gFzvGhwwOsxGgep//VsVX0Q4oXucFhyuN6vrNnz36ou5CQkJDwpIWqzkXk64F/JyIXgbeo6itF5IeBK8APxXLS3wHcBfxDEWlV9Xeut+wt25mEhISEDxPcDInIJwDfAnyiqnZR2vHdrIYO9zB2+2r8/XpDijc81Hhcz/ec5zwn+QwmJCQkfAhQ1d8Dfu9h07712GcFvi++PuiyHwztOg9J/DMdJIPmsl0ztsyPQWdxiLg8lvyEsavT+5X5GWPrDu624frxgybzKA9M75svjKG69LHFkMw0O2MMV76Mmky3Skbrh4xDFdmy/FjCWtQlt1NrQ8/21jvGktU71lZpBbzQbiruksRkNNOTuzYO2+cgrek/NVe6SZRPxMS4bmzsKmrs+OiSsXOLkzKwaZobi11dUVgX/BjK88rBWbdKtsyMJa+3BT9WdN+2Q2QB/diGAUIRmel4PPKl7aevZNh3zSCb6SAVQI2tb9eF6QOmCXYNhGN6756Rr3eN6Q4luAOY327Hpd4BAlRXoN41Xe/okgwJjpoxaKo1i/IHPXZeRgxJk74CjVKXYgbNemRZW6HaN9a53jQm12Qs4HIb0fDjOL1n86N8BgXqDCpPfujwlZIFkxdlc2i2oJsoxYFQXVXqHbHk1yL2pSbmCMxWuvRm2859KIx57ZlbxJZpNpVsLqt+Gc+1r+KIzKHQbivZpRK/2cE8R/Ooo89NPlIcxlGGOCrRM+UaWfj+Ogrlsf2NDG/fnnonMvMFFI0xxLoh4GMCqkAYBerdBrzglo4AkCnNCY90QmgzyBSpgu3PwsURIut37TqrRM8oReklOkdPcbTratfd3K7ZZkMQr0MSbLumZAuhW1OWu45swZAQ68vVvSVbxu100E01nhMb0ernOZ7kWV01Vr3PZWjXTEffjW78PnczJCJ3AFeOJSOeB0bYMOGnxWnHhw1f1k+PjPZHA3+AJUMuoqb74cskJCQkJCQkJCQk/K3AzQiwfxv4CxH5URH5LuCTsGIE3w58gYh8J5b0+M0Aqvp64FUi8gPATwDfpKp7kSH5KuD7ReS7gQz4jzehfQkJCQkJHyZwLaZvnCpZHV0yul7PvGIOXWuv5Y65DfiYdCUxcbA4gtntxs76KtpreZifMeZvfmbFTuVLW3dx1LO6DDrjkBkD2VvGaa6W9BTZQ9dEd4g9pTiytpojgzK+pGSN6a2lM+a73LdBVa0C2SImVUVbsnbd9n1yIQyMYihAOktadJHtDGVkUnv2NjOmullf2ZC51hILLWEQNu61Nhzc7az9kfX1lSWzZY21wVcMiZrdWBAvD7GMK/eNMfRl1JlHjXazbjr1dmr71Duu5DNjfg/PWlJfvuhdWKLtXkc8RlFH72LiXNQ/h0IpD6KTxGVLdms2GFw5eqZy52314BqRLVejCaFnZcWOg9mzrc5btjDmcxb7RW/51o2PrSMX1OmwfoiMc65QmtdhdqWgPdXayMfc2Hgfde8SjPlstuxY1puR/Y/OJ1kdRwbyqFVXm395wvpZu2bzdhOl3ur9ESFfrPqwObFYsmwogTzgtzoIlkxYHLh4vEws7Svro/3+9Brt4+cOrL+5mGyYLY+dtzay3y1UezZ/OzXnEY15FOW+Q7xQjm1IJUw8lAGpPFQBaQQah5tnaBDKjdqShtuoq95VNt4TYl5ATGyOumw/ite0QnEUdegx36I4jNd9ZJPzJYOOG2LSZGfLtuu2vbX7g42CqTmauEY4c8+SkMHafcrocr+tOOKyaX0gn5t+e3JBh3XeKG6GBttj1nrXwj+/zjI/cp3pb8Ys/hISEhISnoAIudlj7T9jFdT1vtTdxIa3e4eA4kjJWji8SyiOLNluSA6LSYjNpg3X9zICBMoDcxPog7nqigVpfYJktrSAOZ+b/MITg9EY2GoMiPs/6m5kiWPVZdvm6LJJLhanGILKUNq7uijhKGVwObCgztozvqgc3GV2ZnVMfOzlF+06g5tHKJSssYcLFejW1QIuoDxiCC7KfTi6UwZ3EAKMrgQkOBanVpKW6qoFJqHo5QbWrt7vWIIFwr4S1u5XDu9cJcr5ce/BbYHI/IwMSae9l3FxFGU+WBuyBpYn1ezZokSiXQPELOk0+jq7WoaESdfGIK+xNheH1h80Vx74lBEqMNq3NvZD/sTAvZcYSWcSg3LPpld7Sr1pgWm9a9sdXTZHk2Jm8qGstnUtd8ylpj9nKOTjDrcW6NYycqeEg3wI5n1l8pIldqx6b+c+WPXV6mHJNUBM4M2iNClUOjwsmV2f4EeBrBbaDQvEy30ZkkTV2fzNVoAguHFHaDIkD9SnhfFbY0inEp1bZHigVGeJib4y6Ui5b9fG+KJyeBeEhSWG9p7RvoTyYBXoDvaOhybdcjVD8mVZdrRNji4zinGD7xyqECaBbKMhjB10juAdWgXcUU5+JLRryv4znD1Yxoe8ZqL2AFOYFefhXW6QeoRcB5edRSa4GlwjtFPr0yGY1EedJYcO1x8wu90eAHuf6+oqXHi2uRgdnbX7imutH+VzaNeVprIHSD+yB/1eVnSjuBkMdkJCwi3GG95zhb9+8PCDz5iQkJCQkJDwmCMF2AkJTwC84Gfu4e/+2B/c6mYkJHxwRNY0X8Rh9mrFhIk3Rs21xpwtTwqz2405Wpy2Qih+rPiJsc8SoDgw5luzFQM6O7OSnohfJaL5kRIqk3o0m8L8tljVsRFbR25Shj7Rz5dxqH+s+EpZnO7lKGb51k2Uds3Yt3LPhv/bjSgbaIVuqnQTZfOdgVDYfi1OC82GRi9iHSz5pueUds2K2/RSlpD1iWc62McBzM+oJYdFW7E+iVLjcP9hTHKcnNdVZcdeQiHG0mkeE78kWq6VJgHAmYd0echgkdZLYpw3+0SN9nUn/8yjmRXSmZ+xc9B7dW+8txuY8XpHBqkLKiadgMFnvJuYVeHyxDFG3Vs7fGkyD5V4DithuQvr93maDR5SxbDZjEmOYue82YhJoZ3tc3GohNJYZPEmUeh9uUNsU7u2kke4VlAVurb32TMWudyz0ZBsCYd3Q70bTPJwSmNyoyXRidrnPoEv5CuWPxSWGCmhTzTt5U8mh+jZ126qQ+KfzaQU+w43ywitsdd51SGNMLtdqbeVtfusX1VX7dj4sfWrZstGhLqpsjhlffPoKTJUmhyqjsYk0nbKMNIQYgLw/LQQCo2jTfGaUSEvvLHVKsgDI6QwaU1oHVkRcKUneEGKwOT9QiiVfGnJmO2GjXQUhzH5dGrrPjzrhhGSnsUuZtbXu7FdT9P77brOFiZ3yudR6uWUcp/hOlVh8Jr3lQ7Jlb4EX+rKrrHvR7KScPXXT7tmcrAbRQqwExISEhISEhISEm4iUoCdkJCQkPD4QWHvWcYGtRvGhPVFL5wX5meEesdYv2Yzajz3VslnqFXTq7eNkaq3oxY3MnDd1LStfZJXqIwRswSzqLXsdGBR200dqt31ethuaowxkRmWAOVe1HRHRtGPY7JUG/XF6xxLDhSkFfK5kNXC7HZHuW8seXU5sscNFAcxaytgNnHHEsCQWJgl2PrymZUvd92qUEZxAMsTGpcz3Wq7bvvUbMDiNmMnQ6nU25bAqALd2BhCH9fTW/p1U7O22357Z0xm1F+7xvYji0mJvXXe5Y/KbHThlFDur/Tx0sGVj8qHwiTNhjI/rUMZ+v749kxku2bv6qDZtn6RNbHwSdSK99Z3y11rw/x0Rrtp1m/1TrTwGym+NGazG2nUzK4K7xydNS30/HYdWNtQakx4VSu17aFbi8l+jeAXGetvGKOdo1vmlHtuSJZrNleVGdt1S9Lrxra+rF31yb5gjebRvi9WRzSNs1nyhVJpN4KN7sxiVUMH7Xogn5kNnRX7ETSzpEZXePLS085La2scaTl4mo3gLHetj4i3CpB2TTBU9cznNrLQX1t9UZm+CFOfWCjBRjk0Fi/qq0q6RiBTvHe0y768oxBONrg8ICMP+wW+tVAzNBlApQnSAAAgAElEQVTayXDNllcjM6+mCV+c6kdh7FpoNvUhxYmsYEw8loV9rreFrDE7zm4arNDURJFOmD1FhyTjdl1XIx6sRhP6pMX+ftAz5RLseusrP1oSspAt5YZvdSnATkhISEhISEhISLiJSAF2QkJCQsLjB2fsNWJMcyiN2XOtMX3ZkkEn3LOfyxOmde4Z3F6nXW8xMHCutXl77WRW97piY6t7trg4EivIUcYy7dlK81vMjIkNhZpLxFiHAhzdVIeiH70tYHlgbeymDCWwNVeWpzv8VsfyZKA4Mq1vs2VMc7MVdclbVvK83onHIhZl8ZWxeb5UZneuHCAGp5Vp1E5nSh01xL5UXG1tbNejNZsoIY/HwxkbeXh2pYXuj5GVyI7HIjd9+6WPz1ncpmQL2992Q4fy2RIY9MG924mv1I7zyCz3unXTVLu2Pw86sL6+1EEHC9YHXCNxFEMHhtyP4ronSrOhzG7XYUTBbANjAZcFtGthYOGBQXfcbMbS2U+RYXu9+4lrzMGkZ2U1j8z32Nj0eif2q8Oc+acfMV5fQic022FwkrCS4Wb5prmNcgy666gNB2tLz7BDLHfuY/+N+uy+b/XwUys97hqxwjNRL69VoN0O+JGSl54QIjtcKpPzjnxmLhpEy0mcOZFAdGdZ16Hsea87L/fNxrHXF1d7plt2vYVjtHeUYPkJxaEMZeBRUBWyByv8YYGf5bjSaGJXBMYPZGidUY1byrUGqTM0U/xY6aZ2LKqrYmXi47U8vV8HB5vFKctlqK4KxaGdx+JQ6CaBUBkDns+h3rYS8t3U9NjW54z97kcEzGJxNdrjR6a97nXfPt6LrG+vtNZWaMqOZf/7Dd7qEhISEhISHh+oYFZtMRFJMwsEe0mGJd1JtH6zJDBbsA/CodrXaB1nAWXWWCDgR7Zu8faHO37AAh77YyZ65SpZHYfxl0TLNLXksjgsn8WEMVfHIe88BrkVVHtm2+XHShff1SnV3irApwpmoVYFq/oYA1zpxCQL+4LzFvSE3P70LYC2gG9+h6KFSSc0+nRrYYFu2wcQRe8VHeUbjXkWuxom77cHhX44O1uYxMT8js0GbfyAsDh9zPs5wNlXLO2BYaJ0UwtQN98JefQhDmU8fzESDKXSbgX8xIb2s4VwdJcldIZMyY8soTNfyJBs6VqzT3OdSWhcLYO3dLsdyOb2u690kHxkjVUMLI5sv/qASNSsAMPIguJ8bu2qdwPlnrNjEqUO+ZEdj/kZpbxq++7HlmjXrts5qrdMjtNXFG22Apyo2Vpf4L2j3KzRQuODkPW9ZtPOh6st+FIHYeqpd+IxWQquE0IM2DSz82QJodbv2jULpBHo1gPtukJmSZDFoe3HIFvCgr/uVENzUOFcIB91SBBmZz3lQbwWKjun3diCYgmrQDvEJMqQmwSpODD5hGb28Hp0l53r4sC8yX0VJS8Co0tRujNaPSi3TU632wIw2l7iRAmdI3TC8mQAf/zJweQXYWQPTq6za7IbWVvyI+HgaSufcpO92LXVja3vmazG4UeBdiPQrFvycn5kfSqfyfBA2K3ZNZkv4uYru49Ue/EhdevYg1msAOma6J/u+odZa3O2hPGFlOSYkJCQkJCQkJCQcEuQAuyEhISEhMcPEm3xNjzibXgdjMXqmcl2XQdZgzHXMti5+Uq58lESi8GspAVdlDl0E0s2k2AFTPK5WXd10zAktvmRMV3LE2YPVh7IwKZb1UhjQy2xTKmuSGQGY0LedFUMI5QwviDUW9FSrwLJA6HOTKrQt8cLxZExzpPzxtg1mwGhZwOxJMGRDolVrotVC4lM4sgYPx/ZWvHRPm1sFQCLmVAeWlvaaZR0RKlCiJUujaE3ltx1x5jzXHnfF4yororZ4kXLvYOnxyHyqh/Wt3PQxUI30snAvta7NtzQSzwk2r0Vh5aYl9W9zZota3ZsMdmwspGAdsOG6rupks+Mde4mils6ms3A4lSgW/dDsp4fKfmhi/KbQKhi0mJlyYPibV+cj2zoyBjxvnqhxmMzHO8mKjsEtFRGk8as+roMVcj3Mha3e9otT3VVaNeVbi2QNTLYMfbHIGRxe0s7L9JF9rUxlrxd11VVSqA4cOjYE9Y8eKE+4U2208tfFEucrDxZGZDS47JAWbWEMqBFYHE6mNylYZBjSUe0OYTpfZaA21tbilrhoG5ix/vwrijVWgj5QimOjLEPmV0Xi9P2u2tjgmCAsmqhs4qSIQhdnePygMtNYiXTjuWspGszdBRop3aMssbkG+JjXyms0E8oTN7hWonHMvbVSin3ZGC3cTZvt24jAG0cQRpf0mh1aH25W9doM2ijCn5sSbflVWdSEDHGuptYu1xnbemvRVHbTrsWi13dIFKAnZCQkJCQkJCQkHATkQLshISEhITHFev32l+Pq/vEQ2dsIqYfBkyPOjbGt0846ouYEBP3QqGxpLoxsOJN2zvolsUKTeRRR+krY+naSUziaqO1WWkWgSHn2LYUPwlDUuBQ+GOyKnLRF72ot225oQ25ko87a2ssG772Xit7Lh4O7xZctAsr9iXaBCrtehimiRfKPYcfm2Z4dueK0fMjY2tNF24MeVYLyxPRpmxkyYF+ogOL3I0sKRL64iGrRLy+iIgEWJwyOjVbGsvalyPvC9oMFmpbgVDC9D4Xk8hMT6yFaWklWHIn2Do1tyIovoRuw+NLYxlt1EBptzzZ3EppFzNBS5vuo+2dBPDbHeFUg0RNb69Zb7e9sZ6bHeIjazlWtt9hx9M1NhIQYtLg4qQOOute602wQif1jg46dAKIwN7BhMmkJssUvXOJlsE0z3d1xvZHm8iLnwTVZUd2mFmC5ija8C1XSYLEgid2vOw45nM71s22h9YhRaDYz3C1oznh6dY8+aFtR1pHVlnRlrz0dPdNWcwqGFn5dD+1ffaVncP+WgiFjZosbrORDulkGI2wBD5jm/1EKQ6dWSHeZsWY+iJHotBuWCn3flSCXNmYLK0zB0HVRnA0WCalnwTycxXuQmXHvAj4dU925EwPHe0gxdv9oNns9c4yJLS6Vhg/KGRzYXnaUxxaH5TOrhPpzBqy70vz0zGH41BsJGNp13l/P9DMzkO7afpu6Xq22s5Vs66DzWO+tETpviDR6HLSYCckoKr8zGvexYWD5a1uSkJCQoR4OLpTcY0zD+mYmCYxKDu6y1wCJDpQ1DsWSI4ftGHi3h3EtZaM6DpLpJPOEuDyw7g+jQlOMYFJggWHJ97amePDvqw8cCeWaJk1JvvoXS2kkcE3txvb9OLAkUX3id4vuJvo4JErMRFtPKkhs+2XV4X57XEbtQW0o0sW5LQblijX+/9uvy1WqpzFACgmkxUHq3X7UTjmtmGSh2K2euiQYFUyCebRDSaR6IfJQ0y+A5PmVHvRk3piyWLNVoiOICalqXcC5b5Dc9uHkCtaWQCqYl7NYeIhuleUB86C/Kmn27CAXcfBpCwnAlTe1n/FEcYBthukdhQHjvwgY3G3Pc2EAgvYBbqtjmq9RkSpLmWWQLrlYbO1wO1EjTi1YHRu/swXniMsb+toTnrmtyvlnqPb8rSnWpMh5fEV+6aveq/nKD0qlKbOKauW5bJgfbIkLzry/Rw3t/DJrwcLVteVMPZR6gJ+3ROqgFtaUmy2gK13BIp9oZ1a3+0fFEJhfWj8QIbUDq0d7U43nKP8MKPas4fIfCH4gxJdZLjMglWd57i9HGkc5Do8uIrvHXai3zUmvelG5ojRO57kMwvEmw170NBco195iLIaSxK0aon2cFBvWyKu5IHcBbL1FspAlimhySjKDucCjDztboff7AhthssDZLYf2VKot6w/jh8UJg/o8MDRP7T1zkGzO+yhluhFH+J1ndUmUeq9rwWoTwRGFx3Npj08NZvBZEOF0h1zI8rnQjETqqt9QqPQbCvdmg4JsvmRJYX6kd2XDp5x4/e6FGAnPGHx9gcP+cHfehuf/AOvvNVNSUhISEhISHgSIQXYCU9I1J3nrx88Gr6/6u0XAHjLuT1e8ZcP3qpmJSQ86aEuJpPNhdEVY8Qm77fkJYiMcEyCGl2OTGIGi9PGVIUS/DQYK9etquSFkTFPWsRh52i3JR6OzlrlOwJc/qicbAmLM2aHVl0R2vUQmWZjuSYPGruWL4wJbjds3fmRJT7mM6HdVGN2rzobPvfmg9xNFV9nlijnLFlrcVqHBKvFKRuWX+4ae9pueUKUoORHwsVnGyPsml6iYR7AfVIaYgmT4/MZ+QJCGWjXlNlTbOi+lyD0zGWzCc1GsMRJZzqPdlNZf48Nsfs1z/yMEspAcehwy8hUr3XU20p9woPA8rbOZBjjQJgENNL/szsDfqtDxt7c+9Zb6qct0YmPDL4S1ryxqxgrLM6m1bsBt94iYrZ0y7sa/G01eKHYc5aUOfKEcWByYo4IhFnB8vYWnXhLcu0EaZwlIy4zpHXUu8GSVu9YUu0uyDca5M45zbMWuLUWKcNwLOy4YNaRUXLT2wYy8rRXK8rcTKrLzNPeP7XjMApkM4eKMjkfLRFjYqJ1ZDv+WW3nrt5VZreZ5KdbC7E/KNNzGfmRMH7AmaVd9KLO1jq6jUBxNaPb6minNsLho397uVVTz0qmJ+as33ZI2G4pjgRaS6SsT1q/yBcy+HCHXGMyL4wfWFUq1ML6USiVyQPW58cP2rXn6pjIObHdymfOZDF5L7MR5k3BaNRSTBq8F+iEts4pCs94vSY7yig2alzp0b0Sd5TRxKqVodShIuvidJS0jPrRKome+DayUp8IVJcsebg4Eibn3JCIqE7N1rNd+YlrZrKqvoJon1AdSvvcbNh56KbRynJuMjFb1vZ9dqclieZzOw6PBinATnhC4sX/7S1843/+0+H7/VfNBPNLf/IP+We/+MZb1azHDT/+ir/mrffv3+pmJCQkJCQkPCmRAuyEJyT+8F2Xb3UTHhf86fuusmz9B0z/8Ve8g+f/5OtuQYsSEh4Z4k2TLN6s6ZptZe9ZyvKUJWdJLDbRJx+KmjayXTM96Pi8IJHZarYsCS7kxlpNzlty2+iisXijy7EoTGUVBjU3vfPyVCA/MoZ0fkZxtSPksDhjjNfyhNnFQSwsMw5mCxh14u16QDpjKLuJDklSg957kdF5ByEWqilNF91uWjKeXzNGWTNLDOy2vLH2cRtamhZ1ek4IY2PAs0bwk0AX2e3lqUC7EfXW66b97SZKuxEIOWz9te2vH5leWqM9YiiV8YPC1Y8xdlqCxAQzR33KdNRaKFIG/GbH6MEMduvh/BX7mWlt5w4/CbDZIovM9vVUTVF1FFUHMSFTumi1Vgbb31osAS4IOu0oqw5xGCs5bXCZJdw1u56w3TLZXjDaNYLEdw4Zd0gVoHNkc4fUGdnJpbHMAUaXHJys2blzj8l0iargO2fbEUWvlnBQrJj+sBoFkThikC2NWXVFINtsWTYFRdmxvxhR3XlEmHiklWj7KEPyqHiBKhDGgfxyjt/uhnUCLE+ZzSEKYeIJI+Xo7o7l7R2LM54wCujUI7UjeEsi7BMj69PeisNMPcVmjapVSgxByETJykDIoLycoYXpwTXvk2HjOQ1CNjfd++K0MehmhQiucaDC4pSxx4uTyuiSo9mKrHfUPreR9S33nI0gBGH/XdvMD03AHnzGeGdBVni6Ll4QZ5Z0y4IsC2ZDOLKk177oUTdV2s1Aux5MDx6vUysqZHrwbGF9pmfw243A7KytK0zsel6eDEMBp8UpG+Uq9yzh0bWmt27XbNvteqA8cIRcaTaC2V+ObJv5zF5bfx2LUAXTg/tqpde/EaQAO+EJiYuH9UO+y8OsK7/ip//ocWzNY4Pz+wu+7Kf+iG/7tT+/5u/66EazEhIeF2gO7Xr0mS0tKS2Mw0PKOjeb0Y+2BYlSENSGehendRg69ms2rO3H5mZw8DT7PnuKBevLHR3KnS9PaKyIaMPN3Vqgm9qfM84S8tSZa0k/TOxHyuK0JUjZ/GpuDn358ljKO1Q6lJ6WALLZsJyXFiiNLWnLtUAZrNxyEaKzhUNHHnLb/8WZDr/d4dZatFKWu7b/fhpY3taZU8koOmasWXDRu2H0SZ46MUnH1Y+xIJXoE+7XzbvZEkm9PQxkWLKeQKgCWnnCbmtBduMoruQsn7kky+0YuVbobq+RLODXAsT4SSv7fTRuaC6P8N6RH2W4RYZOPG6WgRdkq7GkRoDKk086vBd8naFjjwYH7x/hKk+xlzHdtAR1VZhfnNIelmjrLMFvrSXcvkQ2GyaTmmVTIJ2wfOaStbUlo6JjPhvRXhwjV0oW85LsHRNzAGlMHtHLAETtocZX2INXiMmgrWNjfc5kVDOpWrouo2szpHOENW+ykLAqja5ZrBC60ZpPeRaYnrO+7CurSmm+7dgDybRDph0y8mipUFnVQ9lpyB6ooAi0m4Hx+4pV6e5MKasO32WERU5TF+zvTXAu0G3Z+S6vWLJkKO3BqvcY196BpwyxVLw5wDRb1q8l+odrbsem3jEZh8Rgv3f10AJzWGkFcYqcqpluLIeHGBGlnZd0TYaqUFUtxbiluzDGVd4e0BYWfvbVSjUDPw7RS16HZFxz8JHYjigbIZ6nzhKFpRHzFhdLaNQiEEbRL700OVoo7OEmVDpcv81miA+/WKJxBsWR7W8o4PCuVeAgIR6f0Y3/sT6KqurXh4h8JPCVwAL4HOAlwAXgu4B3AncD/1JVj0TEAT8AHAF3AT+nqn8c1/M84Mvjsqqq33Mz2peQ8B2//la+8pPODt//5N6rt7A1NweHS7MUSFKQhISEhISEDy98yAy2iGTA/w18r6r+G+CfAu8Bfhr4GVX9QeCtwIvjIi8ANlT1++K0XxSRTEQmcZn/U1VfAny8iHz+h9q+hCcf9DrU7ZvP7T3k+xvvvfJ4NOdxx/6ivdVNSEi4PsRY5fxIrOqhCuNzuTHSpbK4LQy2WIvTxjgBlAdRapBHL+qJomLyjuLAmETXCKMLxkC6Rlg7B5P7jf2yha2KncQEQsRYOID8KLOqetFPt/dNFh8rRhaxguFU0XLlIS2dbatdtwqUEoQsC4QmM1YeY8u6sULnkJM1xeWcbmrryCcddGZRR6aUaw3OKZrHJLC1ztZTeciVrPfXFqX3GXTzDN1q8bFC4uBtnMX3kUdGJv/oRwum98Uqdk5ptzuTCHjBlZacmF8pjPF2SrsokEVmMpNMkczWTSdoG5MXZzltm5FttvhFblaC6x2SGZsIENoMCWJWbUAIYuuem8lyN8/RQtG9knano6lz5hen1JfHZDNHdpAZu729pCg7xpOG0bghqFBfmKBVYLpurPfebIw/yocqffJARX2yQzqH64Ti0PpJz2JTBOpdj59orH4oTN5RIaJkTqm7jKLo4D0x2y/m+ElnXsvLZyzN+q7OcFm062sdVz7eRjC0NCvHfB5t8FqB/QINgisCbq21Yx9lF64Bd5CjE8/ytCc/yIYkuxCEcFSQTTqrLll1dJdHUIRBxpEtHaEyGUQ/ypHV0G130MVk3QV0sRJltxb9xlthep/Q7nj8WhiSfZtNHapUhsISDsM4oK3Dz3OcxCqOs4KmLiinDdW4NSlLlMjo2NtoSG2jJn5kIz/j8y56WZs0g2DJoXrMl76bmqe265MYxeQl+ZEbpFB2LsxDXFoXq7kqoYw+85se1whuGUctcrt/uMYY7lBAsx4rlxarkbHiQAbLQ/p7yQ3gZkhEPgm73P+FiHwb8HxgD/hc4E/iPH8IfHH8/MXAPQCqegVYAh8DfBrwXlWtr7FMQsINI1xnBOfLf+qhspCv+fk3PA6tefzxg7/5V7e6CQkJCQkJCU9q3IwA+y4sOH5pZKs/G/hmYKErKvEAOBU/nwIOjy3f/3a96R8AEflaEXmjiLzx4sWLN2EXEp5IuFEGd958YHLg30a848LRQ77/lz+57xa1JCHhBqDGUnVrMcnpwJmGuTWWWB1M3u8G5hqxwhH1tiUahsKsx1y8zMcXzLrPLZ3Z80lMrHPK0VPg8Gmxsl0JRCuv0UVHedWZ1jKyq/lMBh1mKIgMs1kDaoZZskX9NpG9zhZCceTYeruxYeqsMEZRdrjS2zKlFcrR3FjfouxodzvCRjcwgn1BmuwwI8uCJfM1jnYt/q5AENykM6Zw4i2xMLfCIGFs7LRfC2RXc9OYVgFyq+5HENQL1YO5Mc/OdPBorGqXKbrVkh1lRg8qdCdapBNjHJe2HwgEL4SZqUvHDzroxNrhlPbqCL9fmIY7V9x+DkeFsbVlIL9QoGO778phTjgooM5gvbV2ErXgE0+21iLvnDB6ILcks2nA77Zkhcd3GfWVMctlweKo4ujKBM0D05NzQhAOzq8zvzi1473naLfN0k+CoGWg2/C0a1GjLqajpzNdvyWzWjLo/Ckdnc9YNAUhOEJwdFHjKyNPt2VFbdxSmKzXUHmkFnyb0Zy0kQktjVklAA6qq6YbRuy4A/hFRpZ78sIjkw5dZjS3t4SJJ78YS5wGS9TDC/WyQMYd/ihnNLYRD7fd2AjFekfY7Og2u5gIHCgOHKLGCFMEXO2sGM7IRo0Isf9mVszl4BkBqR3SCs1WsKqW8ZxaZVU7T9nczn+xXrNYFixnJWRKV2eUZUeeW6Jj25pYX+oYcpbBzufUEnKXp0zTP3l/NlgLutqSiXHRbq+2k9NNjLn2I2jXo669MA05AsVBZu0VJZs502FPou1lGcxiMLOiS/mho5iZfltzG/lpdgJZbZaI3cT0+hovC+mMzb9R3IwA+wB4m6r2QtDXAR8LjEWG1LINTFdNfF8/tnz/2/WmfwBU9WdV9Tmq+pyTJ0/ehF1IeCLhE//1793qJiQkJFwPsdxyfmjewf2Qb7aUIYhd7uowbKuZVVALE0tIzJbmJNBuWrnq5QlzPZAQS0KX5gAhrTC93xxJNP7TiRfq3TAE0G4pwx9osxUgV+pTfqguOQTXdfTS9bJy48gtGas+6am3V+XcywOhKjry0uOnAak8fs2Tzx1SepwLFBuNuXRsdej7R0hhDhCaw/KoMj/nTuh2ulUg7ZSwzOiaDAq1CoatI58L2WGGznJLRBsp3WYkD0JMDltklOcLmu2YROfFgstY3p3GocsMv+FNVhGNhLOZQzUG0DERTztHcTUHURa3mWwFUSS6epArtM6cWcbBguuNFrefE0olH3Wot3mLgww3bdFFjhzl1t5JZw8LdUYoo7RGId9oyCuPbzP0cgWihIsjRn89Ir9cAOC9Y35lYuWzW4HW0W4F8r0Mv34sIXTSMX7KIdXOAr/bWvDUmJQin5s/su1/xrIuCEGYVA1d59A8QGfJfcVmTXNby/R+h3OBrZ0ZWiphVpCvWbKoNCYhyWe2/nYaK0XGZEs5zJFFRrs3Yjqucbkii4xi0lhAudvBVku36enWPTL2ZFkgKwL5ejvIL0QUlhn5OJb7LFZuJZoBHrr1AI0laGplri5aKOPzGW7pCAW0O5Z07FqTzmgV6DY7ij0HLnpp50o2N2mFW2tpFwXtrCQvPa7wSKYsFiWLeUVZdnRtTtdmsNnS1TlShCEhlDy67yjMz1iybMjNdz6UCj6WO7finjQ73jyv94XTf2yBMArL2zyaRalIgGLfZCiusXtKtjR/bj9WQhWsUuV6sORUZ24qJgGx4D2fH7tlRZcbUYYKkjeCmxFgvx7YjVpsMEb7L4BXYfIRgM8AXh4/vxxjvBGRHWAU578HuEtEqmssk5CQ8DBc6zn699+WiugkJCQkJCTcanzIAXbUUb8Y+HER+W7gJPBjwNcBXyci3wl8HPBv4iK/AhyKyL8CfgT4GlX1qjoHvh74dyLyfcBbVDXVuE54VGi6R5GBAPjrCbb/luKfvPSJX0Qn4W85HPhJoNkJlni0oX2uniUVwcAg5/Pod70TTK6xsCHiPlFPc2O52sh2hUmg3vGEqUdzZf9ZlrgknVBdiZURS6XZtmSwbsOY5XwW/XZbseF/bzIVP+qTpxjs5TSzofpQxipxoixOmoc1KuQLyLPAzsYMN21xMZGq3fK4wtbhsoDLA9VGjY9ss0a5SFZ6k3TsGsutVYBMEYHiUoEucmic2aF1Qnuis2qEI6uWqEUwmcrlHGpHKJTqUmbV/EaBfD/DzR2jBzPKC7nNu5/ZNuYZUgVjcxtHcSSEB0cmh7lUGuPoZfCNri5lljx3xaQf4UQDmbLzppzqijG2YezRIHb8TtZ0c5OXuBbaLU9eeqg8OvZI5cmrDpnluL3CWNsTLdlOTTVqLQlyv4yJpyYJWpw1Bnq0s2R5WJkUwws6CpQ7S9x2Tf70I/LdBZM7jtg4dcTmptGTIlCMOnS9Mw/rzGQCLia+hnGgOSzJs8C8LqnKyA4L6NUSl9k5PLozMJ+NmFQNxckFOKWbFUhrEpF2MwyJc82Op92J53ynRUsl2zV5yWxRcXp3H3LFtxnVzsISTzOl2l3YiEP09HZZoCg7ZufWKcsOBYrtJd0iH1hxiMy8QHHg0CrKc0rP+L4cv9mhE28e3KWurCSBMDbJEUWAwhjlXoaEmIyq3fSEJqMYdeTjjiwPhGVOUXX4eU5XZ1RFZ0mfTWYs+36Bekd+kFFezlajCvHaC1X0ia9i388VrWy0SoswWHkub/c8+GnGdkvj0FEYpDj5XPATxdUm43ILR7sRzC4y2AiOeLvmurFJwUIGWWMjasURdBMor8ZEZYn3me3uUd3qbopNn6r+OvDrD5t8L/BPrjFvYOUo8vDffg9I4/sJf2N8/8v/8lHN//p3X+bTn3HiMWpNQkJCQkJCwpMRqdBMwhMGf/SuS/zHe977qJY5nuj4J/de4YU//4Zbymq/59Lspq7vt996/qauLyHhQ4YobuGGqoJhFAYNpul5jUVUMbY4P7Jkq2LPDUUn3MINiYzVJTcUCumrBkprSZJhFNBCWXtfZCTLlW2eFbGxao5+ZCyzCqZRDjC70xg015pem2it5hqJxTZiURiR6gMAACAASURBVJG5aVdd7WJVQFAV6jYf7PTC2JNtNGgQui7Ddxl57glBkMqjkXkLE4+4MNgI6tIKhkgW0GVmSVcjP9jzEbCKiU7NgjCAm3SWxHiyQyaefCYsz7T4sTHhfhzwa57iEJrbLZGx3eksITK36oVaeaSx0QLdbikfyPEb3ZDE6TesmM3ybGMsrYArjamWZcaVv+NZRn22jD0sItNdePIrBdo42jsbiq0lXZv9/+y9edRt513f93mGPZ35He6sWbI8YKZgMGZo68AqZdEmTenqWm3TrJWGprS0TboSAmW1KbgMpgEahlCgYQhx0zCFEKYYjG3AA3jEgyzZlqwr+epO73jGPT1D//jt972yLMlX1pWuLJ3vP/e+++yz93P22Xuf3/4930Fs+7zY1fnWCJd84Cm2V/QmJXnRUJUptGIlGHoB+k5CP0wknGg6DrKm90iCijA6sWDUryTkJHGMBxVZ0mJ0oGoSyssDqoNc9p92oT1O7OHc0JPta7GVKzyDvKZIWzlFh63MAtSapkqwtuvotpq9WZ/N0ZLBJ0WYqCeN8PatWL7pVjjNAMmoJlbCfS56NabrHCc6MDw3I7RyniTjGl9LNzrfqEj7DVoH2jKhWqXYEyWZFV42gFoa4qg9trBUjSKZKpptj1paVOGJTlOd8qhuRgXViWKjiChVrTFLLd3rrsMchu6402wWWtZPA6ZwhKjYGC+pdgpUFyDT3yyhlq611hHTce/jqAWvcNstvhdJ98Uu0q40utHH1zAaOa9Dd294HKqTseNwd8LoXhfWtNUQsy4FNIsSZpV19wUjfG3tOk2FArPQ5HuKZhwwDaSHinbiJezGdCLYCO1I9qecPg66uR6sC+w1bip25jVXZtUN2dZ/8f/8+TN+z7f98jVKxf/0/32QP/7Ezg0bzzPF3/iF9/D6H3k7b/nYjeNRf/ubPnDDtrXGGjcEQR37SNul/KC6ovPGnmmiise+1Uc+1McCpCPv2lYx+ahG1ZrqjJekRwCvMJUUB0cx5CEVP+16S6KTdaU6b1spzNtJ6NLrovgltwqfIgWXkWUomR5HR0zdiSidwpSKbE+THSh0LVHm9UZkUWYMsobQFUa65/CLBPtwfpyw2tYW11jUbgpB/JFV7nG1JZlr8Ze24n5gEnF1iEkkRlC5J5RWjmMrhaBaGhEhBinOVRLQqac54SEqcVlJJemPNFBti4AMjRTCOhLTgG80+aMpaqOhPd1gM0dz2mGGbSecE9qO3U2kwElFfBqDQi2suIQkQRIqoRMVesy4oZ1lUqTrSFK04sxRWuIspXdyiZ+lqMtCSbH9FmMCdZ1Qlim+NscuDqrn5KFk2IKCYlhRPzpA15rVy2oGd0wp0paySag6sV3ZJOxfHXFwdUg1z4g9R+98QlxaoS8UTr5r5GGpOiXOLMNByanenH7a0M8abOLxZ2tCL6CvZDinCRPxe66nOYkOxNdNIQlkeUNMAmYpVB1TycOQWWi8M1IUbjbUdcJ4tMS1hp15n3FR0Z+U+Eb8wXXqqfcKYoQk8STG0xtVTCZL0tRTOyNOIt2DltlLjt03Yio0LNIgDiCtlgcVBWo/FYFrErEzQ+iKf+XBjTy0GrUy2L0Eu5ug++JM4nsdbak0hL2MJPHojrJUnFvgWkNiJLFxscqo5xm9Xk30Sugk/VYEh315uI5p5xLSpTWqrsjXc4tyCr001JseuzDX7gude83Rg67qPnvMuvOvi3c3lUSkq0a+WzcMQguJHVVtJNe6z6AZyQP+6qwnpHRFdVeMV5rx/UaK7uvEusBe46biK3/gLbz2B18YVPujePXD1c0JavmTT4jl5AOXZzd0u7/5wQs3dHtrrLHGGmusscbTY11gr7FGB9dRQ773t++7ySO5PrjrpLK89YG1V/waLyB0froooWok087OLUC75aCbmo2pCIuaDY/rix1ezMTn140901eIx3G0IoqKXbqgG/hjIRahEzIN4rEloG6l61pvCy0gZp7Y2Yb5QcCUR55+0uFtN0VgpWdWvHsz2WZMI/UpT70VaEZiFRizQDvxVPOMwrbouRWBXyV0keZsizERY4VOoU1En64gKJpTjthomCYiyMrERs/3A0qL97KuNdoGlI7opRFh3rhFWZkmjzYQVxY9bNF7yXFnFiCMHTEomU7X3fS3U4RUkvViaWUqvtVU51pCbVAKXGtQmVAQVCNddSL4M7XY8zUaVCSurHQeTUDZIPSDzs4u7TVkWSuUgzM1OI1rDX6RoHNHemJFaj3pnojK8q2SQb9icdDDryx+ZSXhcODEJi0obM9hE0/Sa2lbI/QADRtbC3pZw6LKWF0cEOYJfj9j9ekhOuv8wyOolZXkTaeg1igj9oYhiUIhyOQ4h6hIjWda5mzkpZwbUbqboRfwzqCMzABgA4dlziCvJe2yW9ePfGf5GMEJfanXr1GpiF1dY4hR0R9UNHVC4w3bgyU69bgqodev0aVYJlaVWBIWacsga9jsr6jKFKUiaepg0uDHHj1oiT3x/3Z9Eb62Iy9UnLLzdM/DMf3CbThiEtG5eLTbUeeLpxEv6dONfO4swNCJ1V4SGd82xXvFvMzIzqzEQtB6OW6XEmLQ6MxjdSDptaSZE2pUaSAJIiL2inYUOntAuT5jKn+HfifMdN0sVpcCmu6LoPeoMx1LS6yMdOaP0h9HQveoTjtCEXADET/HoRNBbhpotjwqqmPRLVkgDsTyT1fdvamz8pvfEY4pPtd1q3vGN8c11nge8H2/fR9f9QNveV72deFgxeXpNVrIex6+uRHqD1yef+6VgG/+8T+9rvWeKjp+jTXWWGONNdZ4brAusNd4QeCL/uG//YwExl9853mudpSN5xpf98Nv46t/6IVBUwH4nQ+LMLFxgTu++3f56bc/+Ky2dy3vaY01XgCIXdDJhpcOU+dlpbzwU1Wtu+72tSRHFeRfMxeRGyZiF4p2chQIIj9lutSotgsMmQtnlzQQCk87CrTjIF28CHTJiXph5ZcwKtlnBN8XOzACwgu3wudUTuzmounS7zIRU7mRhHmoNGCWho3tOaVLCEPpGqOlM4iOeKcJXpP1WklFDEq6ch2nNXZdRaXFRu5I0Cj79igNobLHQR2x1sIPdwqSiOo7ohd+q9pPiF0X+7ijqsTy70hQelwFJNL1T69YsTPzilhrYqMxVjq1ZqNGrQy664qrlZH9dt2+OGmxmfB0o5f7TtGXpMG6SjG7KcNBie63hNKiMk/Rbxj2apZlKil+Z1cMiprWG+HkLi2m5yAo8kFDOFkTI4SgaMsE7zTtQU70mpMv2wVgXuas5hmx71CFJ79kxIrvUk5MZXYgFp527Il96fYqBaqQ1L920vFsFwkRaLzh1HAuXdnEwSKR76tVuFpEmrecPsCkgflen1WTEL2irlKyjQq9NNilJlgRCRKhn4kwU3Xn+HxRYHWg16s5mPdog6bXq2W2obHYcyuUivR6Nan1NE74yEYH7jq1Sz8XIWhatCJKXEqgSxg54eqvDGSdIHPkRCybBJKZCGkxkXTXEJwWKzsl36mcI1GEttNUwpKSgEk9qnBMeiVJ4oVH3i+JUWFtwAdNvHuJTeR6q1u50BPjifvp8fnjh57kQDrFuta4QYBWke4adCnndkxE9Koc6MzTv6Cpt71cb5WMnQjpnsHuJiIO9nLt+6GMUzmFHrXHNoSxPBIhQ37R4AYRFSSMRidyXSsvnz30rtkH6vn1J82sC+w1XhBYNp7v+c2P3OxhvKBQdg4nP/P2h57Vdhr34oiEX2ONNdZYY40vFKwL7DVuGp5IXfjgIwc3aSQ3H+89/9m0lJ3Fjengv/m+dbrjGk8PpdQ3KqV+Win1vV0I2BNfz5VSP6WU+l+UUr+glLr3ca/9mFLqh5VS/0gp9U+UUk//u6KjxE0DxUUrjgQK3Fjs5ZRTJPsSfCKdZY6jr5OldGnN1NCOwnE4i+93XamOP6ta6eDqVmzHADAcB1YQQa/0cXiMKoXPqSstwSalFv5wVLQbHW9z4CQMw0qnK/bEZeEo4KLdcMQItoRe2lK2CcW4Inrhmxob0EnAXS0kWro1EjueumP7ObstVLWjoBMWna1a0DIm07mIJAG76DiotSaurFim7VvpipoImScMPYNPiNuHuZyS5i36ULqrqtEMP2mlEzsQTi060t5WoyKojmuaDhtCUITdDKU7HriJx3xX3YgTSRi3pL1G3DEOE9TC0ju1JDEe1xrCYUp651zs9BTQKrSNDIsK56UL3bt1zqhf0ThDXSUypolEhmebJcYEtI2YNBD3MkzuCEvpJuvUH1vwLae5HL9Ww9JSv7Ik7TeocyUkwn8+e3afE7cfUIwqotf4RhPrbgaksw2k79jslVQ+YZKVXJkPGea1ONEA+mRFejFFq8jJ3pzbT+1RjCsWs4LtE3OCkxmK5OySZsMfx7Urp1jWKUpDmrUY69kYL6lbS5Y4sqxl52BInji0iTTTjF7eELxmUlT0khbnNVpFfNBMshJrPDbxDHs1yVACf+JKgoRAnDqOLPg4mi1KAv0LSlx6bKDdDOhpgt23tGVCtqeh68+E0opWwQnnPkkdSe5ovWGjX3LriQNCVPSzhiJrKNKWk5MF1nq0iaxm8p3M5gVMWolqL/xxaI3ySmwqW9XxvjuthtPiSGMjrh+JXjN/RQuFJ1aGqCNqIed/Owm4icMeGuGTJ519X1CYVTfLlXhoZJaLILz48o6W0PeYlZbQms51R24O1+4/6Z4RS9HrxLrAfonifef3+ck/+uRNHcP5vdWTLv+aJ9A1ysbza+/79E3lEjsf+Jk/foiqfW66wf/Zz777s5Z984//CQCNf2bplGus8UyglOoBPwP8zzHG7wW+RCn1DU9Y7e8Cj8YYfwhJ6v357r2vBb4hxvhdMcbvBL4OeN3T7jAgVm+Fp7yjIfZFzKecpAeqCO22Q2UidCLpKBhZoDzrRHhWdEVaJwSUtLlAGDjcyEtqXeGF8mElwe3IW1pX3dTxZnucNMikRQVFmDhUGsQ714ttGFoszghSAIjQS8RiRwKxmEaZco+K+oTYqE2KklGvgsoQc4+xIv5ioxOPRUXSayiyFkwkGdZ4r1G5xw+6+8yoJZYGbYJYA9YGpSMm7dIAj2qATvzo+4HQGBFQJgFVahZ3iqVdvLUr3k9VYulXeOZfJIWYPirGunH5kSftNWAjxgRCbdAnKrEV9KBUxB5YYh6IpytUKeNqayuFWN/DqGXUqyjrRCwAe47NwYqyTkkzx8YtU85uH+KDpqwTsq2SE8MFIcJstw+ATT3FoEbrQJo6VvOMsJsRA8diM5V7kmHDme0p+/O+UG5qOQb5RsXZu3c4sTknBvFqvuPWHc6NpwyShn7aMO6X2LzFZGIrp1vku00C+aDmYFVwrjdFE9nsr5hXGfbWJdnFBGO9JDMuExZtxoliIQ84OtJPG4pBjasSstSJcK7w4rduYLHbp9+vyBJHmnq2e0vytOVw1uPUcEGaOarWkuUNxWZJnrb0ezU+KqwKIibUgUFaU7mERAf6udBO2nmK6TkRuEaxNSTtHhoGrqMWGYiKw1c52k0pzo+SHt1EvNbL21r5LqM6PtY0mtBqQlD08oZpmeOjorAtdWupW0uROJSKZNZxbjxlY7xksrmk36uFnhQ6WlEmQltfiIgXK1QQPWhFSFz4Y8vJowflWBm5Jr1QzfyWFOtqYYkqkuxZ3KYjORDhqNxz5FqO+6kUz10hrRLxlVeZeIL7fkDXSihWI3ecZHkkaG1OOhnTdWJdYL9E8Z/+zLv50T/8xE0dQ3iKgvni4wSHb/nYFX7w9+7nO3/9w/zpJ3efr6F9Fn7+HQ/zxt9/gO/89Q8/J9t/4qH4wd+7n9bLwqpdF9hrPKd4HfBIjPFoyuSdwLc8YZ1vAd4NEGP8CPClSqkRsAcMlFJWKWWRkvPh52fYa6yxxhovXKwL7JcA7rs45epNCk95Jnh8YX2Eb/vl9/HP/0zSGZe1+6zXnyucf0Ki4g/9/gMA/PaHLvLg1cVzvv+f+5NPPef7WGONDieBx1vXzLpln3OdGOODwM8Bvwb8CvAW4LN8IZVSf1sp9T6l1Pv8agE2YDJP8bAEXajMk+0YkgMjlJEkoEyXLHgkKgqK4jGxvaMvlmLqSAgZuk6V0/QesTQTsSXzYy+2dqELjlFI+p+7Nv2rS4PuBGsEiE6oFzGXrnmyLxZxeEW6I11ec5DIPpMoSYqmo2VUWjrfwO6iT+MMvU+LmMq1RizLus+eF9LJ9lGCNHxrCHOhb5AGglfY1Mkx0GJPSN8JLeAgw846EaBXMtaoIBMrNIAwS8TCzx1RVDz1PMOtLIwc2UCep5Kixc8TzKiR0BEvossQFLZwNHUi9BXriaXBnWyxiceNPemoJslkXOZKRlgkmH4LtWZra4EPIuhMU8dwY8WyFnHb1nDJKK8JUbGsUrwzZKmj8YZVlUFQGOtJM0dqPaoT+sXQWfXVhnyrlACdvYR+ryazDu809UGO6jluPbvPndt7bBdLTvfnvOrsZW4ZHrKRrdAqsrPss7voY1TkxBGVwQb8uJsZcIpxv2SY12TaMWtzEu3pZfK91bfV1MsUM2rBaR68dJLKJfTzhtAYpmVOP2/QSaBuLMoGsXqcOFSEZFjTOoMLml7WkJuW1HomoxVGBQZ5zfzikKaWbWolloGNs9TeMikqDlYFqzblympAL5FxOa8xfYe1Hps5VKXlOqm0BAqZgO45mYHwEtaiVxrvOnHxRgOZJ7mckgwasSB0SgKNWi0d+NpQzzJ8VJwezTEqcnk+JLX+uMu/uzdk1Sb4qHFe088aEusx1qP2E0kurc2x0Fb3nFxngDHd7JVXqL6Dw1SoZUepjF4J/Sd2lnwqShfbKdrTEmLTbng4SGUbNuBOdiYKsbPZHLUi3CwNsZR7TEwCfuKOk0WP7inpbkdZM5H0qn2ye+iTYl1gvwTwLT/xDr7qB/+IcBMjwJ8M//qDj33Wso8+Nr0JI/ls/NV/8s6nfO07/t91OuIaLypcBYaP+3vULfuc6yil/grw+hjjX4sxfitwJ/DfPHEHMcafizG+Jsb4GjPs39jRr7HGGmu8ALEusF9C+L4XWIDKT771s+3n/sOffMdTrv98Ph5Myxb/FA8k8Xkdyc3FonZ8169/mHl1c9It13he8G7gdqVU1v39tcDvKqU2OxoIwO/ScauVUl8MfCjGOANuBS4/bluXgPzpdqYUZBelU1uec2KtpyKuiLRjsQ4jKEIXE606kSMm0mx04SWdrV086lzbLljGRFa3OmLu6X8ylW5VVNc420cdbydx37HnCQOHLyXgBIBaC1/VCR/aFVG4yAtNO5SY73BCuMuoCLlwnUHEayjQKpIljqpJWN3mSK4kxMcKXCVdQ2NFkOeqhHKVCYf7ci7dutqA09jU4RorYSOtORbyhSjCLDeR7jaIvVx0GloJdolexqF0FA7t0NFMM4pxJaE0TknHu9LYxGNHjdjFZV3AjVe0hzm+1fh5gkoD9VIi3XXiaeoE1XMYE7CdYNWfbCD3jAYlxUnR16zqFGMDRdqSJ47phbF0SoF5nbIzHdA2FqUDvazhyt6YtrGk45oQFM4JP9s7Q1MlZP2G0daSs7fsc3Zjyu2n9rjzyx7j1HDOzqJPu0gZnFxyy6kDTvbmWB1YupTDuiCgmLc5u+WAC9MxB3sDqjLl6uEAo4RrHo8sE5Xw7rWK9JOGpU+5NB/y8YfOkmj5vDoJqJXFJsJv9ivLwwebbOQlxahi+ukxuhMDto097pyiIiENFHlLUyc4Z2idofIJt48OSI3nsCoYZxWDM8LpLpuEvVmfqk6Oj13o+MUX9+USXbUpizJjvijwlaGeZ6SpJ+aB0MoxNzND9Jrou/O1u27C0GMey8WacWXRSaAde9rKEtvOprK7JkIWJHhoalHAoklpvPCdj34y6+7zHsx7XNifcLAzJDGeYVaTpg51SmZPzKGIbGN3/uqeBE2FqMQKMiqZUcoCOvXgu/jyWmOncs3GRstMUhQthMkkXIekC4VREL108WOnbYhZwOwlEgAFqMoc22keHROsdKyv3bgiNN094DqxLrBfQvj1939hR2a/66Hnn4P98O6ST+0895SQFyp+8R0P8yvv+/SasvIiRoxxBfx3wE8opb4f+HCM8Y+A7wb++261H0eK8P8V+HvA3+qW/xJglVI/oJR6AzAGfvZp9xcU9a0NYZGQX7aEnic4LdQQK84G1Bqzn6BWlqg7T2wdZXq9m87FKaFpqIiaJfIDGDl2H1ne24gjgFdEFY/dFMxKpsqJoJbd1K9XKKewu4kU806oHrHVZAcak3n8xJHMO1rI3B67EABSxDTiXBBVxKpAbiWxjjTQnmngbCXuBYD3Mm0untQR1Sj8RLye1VGR4c1xoeydhtrgZyl+Jg8OKhXXj9D3x+mOaGhri1pYSVjcE7pFbIU2kFhPbDWqNrSVhSzgu2LLH2QoGwhlR4MZNcTGQBqIjcZ2hYsyURw3KkO1kgRBFhabOTa356TWE4Ji98IE5zR5Ko4XqzolZp6iaNhf9CjrlOYgBxWZDEtmqxxfG5SKeK+JQeOckcJeiWtJljrOjGZsFVLAF7alsC2LJmO1zBmeWPCyrR1O92dMm4JP7W3x4IOnubA74aHdLR65usljOxPa1mIyT/CKdpFyWF57JszPZyLqqw2tNxxUhXyfiWOwveTywZCmkgfEmAaaKsFkQpdZfGrMQVUIpaOSdMM8bbuHHnHk0HOLrjVGi+jVOU3VJFyajUi147bhAXuHAw6qgnPjKdoE6iohTR2nJnNmy5zDaZ9pmTPIGvK8xajIvMqOfaizYY2ygapM5fzuzkM/duKbvrTygAbH3vOuFzCzjrIB8oC2tGAD+UUr10ijSPcN2kbCVksElrW4qNStJUZF6w3DXo1J5OErBEVvUrKoM4ZJLZ7eiTgG+aGX6zIoYmkIlUGZQHBaHhjT7mEnADsZKihxAVIQj3zsc49ORDyKjiKA7bzk010j10EEZlZoZyAJkhMn159T4lTTUaliJUmfOIXKutTTE05oZQFi//qpqtdPJlnjCx7L5gvbD/lNf/Yo3/8ff/GTvvZcOIxMy5bX/8jbn2RfN3xXLyj8H7/zMV531xbf+KpTL6Fe/UsbMcY/BP7wCcv+weP+XwLf8STvWwJ//Tkf4BprrLHGFxjWHeyXIG72dP9jhyV3fPfv3tBtvuF3PnZDtwfwpk5c+VLDz7/jYb7tl993s4exxosVTolvrYL6RGezF6UzdjQlq4LCb7REGwhjSQZUNmB3EvHPdVp8aoN45sahOxY8JvsWdMTsy7rU0oUVSgf4LB6nI0pao0L3HNFE/OlGpsIBhi0qCVRnWmK3qDnbortpdyJi72VFNEYrU8z5FfGiNjqQJJ5iVEFUFL1a0uQeR21JixZjAyEL6NyR9hps4lGlwZeGtNcSnVBoknGN6kkineq7riMXu+RK2Tc6om1AbzbEUUu2p7H9lmQoU/KtkxTG2OuSHXUkeNk+AbHq63y7k0Tsy2iVWAc6Ld7Cnc+26YsYrG0NZrPGXyoIQbM/7VPPMvSgJUsdISpm8x5GB4bbS+rGUs4zysOcZFyzOVoxX+WUi4yk16B0IMtaYlQoIMkdfpmweWbKnRv79GzDXtnj6nzA1eWAvbLHxSsTtPF8xekL5MYxrQseubrJ8qDADlu0DtRVZ9GmO+vBg4w4S0n6LfP9vviSryzVuRa1ElvHI9u5EBVGRU6P5mRZd64tkuPua69f4Z1hcNeUnYsTMuvQ50rqKj0WRSoThJI0Fpu86bTHoFdxcrLgZSd3cEHz6HyTW3sHvPzsFVLj8VGzNVqSpI6msfSShhPjBeORCDW1ilgdODuYcvfmLlcuTRgOStrakvcbofcYmelQaZAZmkZfSwFtjHi598Sq0m+1mKWWWQwbUWMROVZnnVAuhg5dK3yjRTjozHEi5bhfcnjQx0dFZh0xKs6MZ2wMV6TW44MioBgPSrGmDOK1rlotKaeJjE9b6biby6mcewrxgNegnAgRGbX4gZeOvNOERQJbNXplZNYGSXyMlmvJnWkk1oa4tFAZoad4oVsd7VM36tiSEA366H5Ud11wzTWB9HVg3cF+keNtH/9MrdK/+sAF/vVfXLxJo4EPPHrApcMb72jyi+88f8O3+Xzhe//NC4cb//iHr/e/hIN/1lhjjTXWWOPZ4IZ1sJVShVLqw0qpH+n+frrkr7+ulPpRpdT/qZT6bx+3/A6l1M937/lZpdTgRo3vpYpfec+nP+Pv3/qLi3zs4s1x6njw6pz/5KffxXf8iy8MFw71FMs/eYNt+n7pXedv6PaeDf7xW66FD33r//2u4/+/2GkxazyP0B0nNPOYhT4ObPG58K9jq4XneCQ0OrKBj12SYxpgbo+T6VARtRReKF7hepLs5ocSYmGObP46rvWRWOs4MKYTgMWehGsk+8KvPgoMoUuL1JkXfmhlUKkIAZWJ0kE77iJDMw5YHdjIVjhn8F443HWVMLhlRpa3GBNQCkJQsp+eJ7SGImvJ8paYBgnBUBFzJWX8zpwYFcYGoo4kmSP2PHFlMRv1cYddZx5rPWnWglc0ryil+514fCX85ixvpUPY8VFDULjaojcbzLCVkI++dKyVjiQHVo5DhGRSkaSOrGhJsxZ/mIoF36Bk6+V7lHWC280xhdgQptZT1Qm+MhgdGOU1bW1Jcgn0aSvp9retwaaeybAUTrEJJKkjLxryouHsrXu8fFPcH6+uhly8tIHVgd2HN7m8MyYGxb2ndyhMy5VyyIMXT5CkjsHmiqJXM+xXDAclbp4w6EuD51Vf9CiveNWnmYxWJL2GdpUK/111PNuo0CpSVgkPzbalA5/Ie/OiIT+1FOs6L93t20/tsdErsf2WxhsG/QpfG3zQ9Ho1sTbynZpA3G7Ie3J8Gm84kS14aa3gfwAAIABJREFU5YkrnO1P2a0H3DPc4exgysXDEVVr2Rys0DqyaDIS48kSxzCv5dzp7PvGScUdt8kxGgwr+nlDMumaWV16qRt3AsC0E/IdpaTOrdhHpoFokBCWTM5JpcXGj1pj0kCzKeLOUBuyxHF1d8TeVCwpddIJXqPi9lN7GCVhOOOiYlxUWOXRKjLplXAkttVR7PpMxPcCwSlirWWsnfjQjx0hO+JNy7jzKxYzaImNRg9bQmMIA0cYyQxBqA2huyfELjgIHY/fH/JOyNpo/Equ+ZB1szqNwQxl5kp1M1/5JStBO+r6fwxvJEXk+4EPPu7vp0r+ugX4+8Df7zh+36aUeln3np8BfrZ7z0eB77qB41vj80DVev7gvss07tmHnewv104UL3S4J6RG/thNDiNa48UI1XnQRkIeUZ2oyI2lYCSKE4ZaieDKTC3JoSF5LMX15AdTN13KopJiXXl1XGTGQmKV7cxIZPrAo2qDnlkpxruiHBDRYYDQiFiKw5R25MWh4DAldMmJR4ilRa2MpOBpeZ9aGajE8YRWkc40Vslg2sbiGoNfWMbDkqxzD8kLmVYP3mCtx6Rdol0XNT05OZdUyFlGcvec9pumFL0am4hHc5a1FJMKlXsiEGcpNhVXj3qeUWQNKMTBokxY7fXEQURBudtDz6wkS2ae0GqyfiPF4NKKuKwWX+TQGNpTDf1BJXHTJpJaL44bUaF6njxxkkZoZLk9UTIarjg5WrCsRMg42V6wLDNWTULSUSyKfs1kU+LBFXB6c4bzGoXUQGniuH3jgFefuMy9kx2s9kybnMNVAbVhvsxJTpRMJkvuve0Krxxd5vxiE6sCSebo5w2jouLerR0SE2i94YtefoGXb1/ldefOc9dgl3uGO9wyPGTYryhGFTb1jD+cSDx3Ks4mpzfmJEZ8xlcupZ81xKjYGKwY3zol6TesqpRhUrOZC51jWaVYEyhGFasmIbNeqBkrS1yKk0yetvSSltw65i5jO1sya3MulSNcMNzZ3+PkaMF2TwSd28OlaPWqDKMitbM03uC8Ya/qUwcrriVWnGZqZ8gyJw+ejSYurXh2K1CLjo4VIdpAHHUFqleEsdA3YmnEo15HwlDOO7+yhKGkGSobxMlEwXhQkRhxUjlCoj1tMAzTmswIZcTqcCyKTPoNdi9BV5rN94qvfEwj9mKGmRtUUEIHabT4zBcegsLuyTGsToonfL4h56bdSzCFRy0MyklKY/8xjWqVCBcbTTKQ60JFRbTyAB27h8fj4rsTUfp5QoyKuDLoWlHd2hKdQh+JrK8DN6TAVkr9V0j61+MTvJ4q+eubgPfHa6q0dwPfrJRKgNcD7+2WP1ma2BrPAQ5XDdPyyYvf7/vt+/jb//z9fM0b3/o8j+rJ8Ykr88+90g2CeqoW9osUd3/P7/HP3v3S5J2vscYaa6yxxo3Esy6wlVKvAl4ZY/xXT3jpqdLBnmr5NlA+rvB+sjSxo30ep4Lt7HxWaNgaj8NHnhDc8sef2GF30XzGsi97wx/ypd/3B0/6/k9cETrE7qJ+0tefbxwsm8+90g2CepoK+3DVcLBseNsDT8zj+MLFU/l+r7HGDUXXPY6NJk5aESIeBSs24ncdm86XutEEC66INKdbSWfzMmUc+x7SgKoModc5JNkjj1yNL7pp8DSgWiVdOIVs13bdqixgFwY9lSnv2HeoVuM2nXS6o9CjYlCEZYJyijgQD2B7KEmKMe+8uzvUJzxWeyqfYKwnzlJIIpl1LMpMEvp2+2z0Su48vUueOGziGZ5cUK4yoRRkDWmv4fS5A/K0xepALxXqhB015IlY7qGj+AqPG7QWz2WA1Eq3r14lx2LMprEspzmDUws4UQtFJIqoazJYSbKjjSRFS7pZgYK035AULSFo8oF03X0nAuvlNcPJitw6Dhc99hc98rSl31FDWm8YFDXn7thlmNeM+pUI3zZmaB0732QREg4HJZNc6CytM8xnBeOi4lQ+R6vI0qU8sH+KvWWPtjUMT895ze2P8vLTVxnlNV+x+Sg907BoMhZtSpG1vGLzCl994jyvGF7h608/xDfdfj9fNrnAywdX2EyXzF1O6VNu6R1y98YezmlcbZndKzQA1XfMypzEeE7k8jvoo8bqgNbiTX1ysOD0hpQzl5dDcuN49elLWBNIjCdPxUJvUWbSMfWK8QMWNUuYFBUhKgZpzazJOWwK7hnuMK1z7p+ewgXNPaNdAopZlbFdLI6/29pZllXKqk5ZrTJiVDTB8KlPnWK7tyS1jvnlIYuDnghY0yD2lEAovPhB6272qEtMjJ3tpZpdSylN9g3B6c43vuv0tpqkaIm1YT4tuOP0HreP95nkJYOtFa03VE3CxdmI2ol137JNmdcpizZj+eiI3UWf4I3QQLxidUauNeUU7clW0hQroVyReaFidT9P4VwFidCq2nmKtXLt+/61a1CvxOt7+ZqS2PfSdY4QvFyzRMAGYiXWmmbQCmVFdYmu3TEDoPD4QRARs9OE4vrd2G6EyPGvAZVS6ruBrwNSpdTf5anTwa4C9zxh+YPALlAopVRXZD9ZmhggqWBIPC+vec1r1lXBk+D+SzNu2+zx2GH5eW9jWbuXtNDtj+6/8pSvfc0b38qqsz388Pf++4zy5Pka1nOCK7MbLzxdY4011lhjjZcqnnUHO8b4AzHGN8QY3wi8A3hPjPEf89TJX28GvkJdaw++Dvj9GGMLvA34ym7513bbWOMZonaeb/7xP+Xb3/T+z7lu1T7109gX/e9v/oy/f+wPPs7es+hk/9Dv3/95v/cIz+fT1AcePXzK11aP8xR/6/1f+F3spzsP4DM/7xprPFuopT22w1Ktku5QGogDL5xnpyCTDlJxWWOXIihUXSAMCuxuArURy7GOP5lescQk0k48ptTEPKBMJNvtrMA6QSNByf8jpIfS3VYrSVCMoxaVhuOuuEm7hL8IZindPD/0uC2HslG42xrpqg0cOOnM7q76eCcdM2UCjTfUq4Re0nLizFTCOboO3+ZwiVGRk5szMtt1oVPHOKuYLQoaZ2i9lsCRrEWryHxWkOYteSrCSK0j/byhNylJdGD7zFQ47IXwcE9szBltrLA6MBqWZEmLUpGN7TlGRawNZIOaGIXjbR+R8JUsk8CcImuOO7K9rKGftgzymoNVQZE1NI2ln7Y0zlC3lscubgKwWaxYNgnWeA6vDhmnFb28pq4S5o+N6OcN927tULqEEMQy8KvuPs+XbF5k7jIenm3y0ctnGOcVt00O+eKzF/nWOz/EV4wf4eu3Psl/dOYjnEmnfHJxkkFac/vwgNedPc+XDS+wlSxpoyFRnpGVJsLCZVyth7z/8i08ONvmsC3YSFfS3ZxZEcHaiLGBskx5bH/MMKnIjMOowNXDATHCbFFIt9y2JIlnf9ZjpxqwnS0p0pb9eZ8ibVmWKdUsO04Rnb66RZ+ojnnJiyZjM1uxV/UBuH14QGYcDy+3cLFLvdwRvwcFjNKaEKHIGsZFxS0nDphk0kjbPjslRMXhYR+SQNpvcLMUUziSmcYvu+RCLeFMcdRes51rNToJwnvugpjc2Ub0BlnATq3YUdqAaw35hnDWLx2O6NmG1HhWywznNa03TIqKqwdDHpuO8VERgmZnOWD7nj2xi9RBushJpDrpULVBjZtrHOiRJ90V4aQ2UZIzU+H+69yJJmBmcM5gLmZEEwlOoTYa/EYLlZaud6MJfY8aOPzCCrfbRnqfSkXvUXh8bTC5l9d6XnjfrgtoSoMIHAfuWmLsdeJGuoh8K/DvAF+tlPrPeYrkrxjjBeBHgP9LKfWjwD+NMR5ZF3w78O3de74Y+OEbNb6XEo6m+t93/nN3n1/xv/3b697uT7z1Qb7nNz/yeY/rg09TsF4vXohuFn/+8P7NHsJzjl9458O8/5EX/+dc4/mBnWuwAdV5VataS4HbFaNmqbtkwkizEWk3vUzn5p7YE3cBd6I5pnFgIqHVNCcdqhCngdC5jMTKUJ6VolU5RbJvSHYt4/ssqjKUZyVNLlrxx9ad08PRduPjdL/upCS+ASJ2dBLlrJOuGLcBNhpcNPTTBj9LhJaytKzqlP6owgVNL2nFDcK644J6Ou3hg2azWJHoQGY90zrnntM7rKYFyzKTgDlnWDUJ/WHFZFBSpO2xv/NGXmJNYFGn9NOGrc0FMSjSrCUznlsnhxxeGjFf5kznPYz1jPKaVSMzcE2VMOjVbPVX6HsXDHpC6yh3e1RNwrio0FpSKhtvKJuEPJHxb4xWHKwKVt262aCml7TUzpInjlWd8hWveJiebSgSR5a3nL17hy8/IQnDmkietvy7tz3EPX2hfl5ejiQyvKiZ1xl3DXZ5/dbHOZPKb0miPD1ds+/67FV9fNC8aniJLxs8ShUSLtQbvGf3dh6Yn+Kh1Tbv3LmLtz32Mj509SybvZLWGx7YP8W0Lej3K0lYXHSi28qyOV4yGZQsXeet3D2I1HWCtZ5LVyYYHRjkNUXecmU+YOFS7pnsknSfOXhz7VzKpEhMU8eqTXFBs+yO/Va+ZNoWANzaPyBEzQcu38I4Lfnyl5/HRYOPikWbMl/mxxSbGBVaBRZtxmaxog2GJHNsnpzhnUEPWkKrqW4RGoQ9sJgrKTH3ojPS8pCoWkWMoPpO3HW6JFO8CIrdSNZXnTiwXsm4x/2SlZO49CxvWZYZyyt9ESAWDU1jWNYpk15J4+S6OEqcBK6lrwahYuncQS0ixWbbiwMIkGZOxqfkYVonHj8Stxt3qoHMH0fAJ4NGHtCvZqi+E+/3VhJcY8+jas3qzlYe6r061lvFzg8bYPiAXLu+NtR3VWgbsPuJeG1f733uutf8HIgx/gbwG09Y/FnJX926bwLe9CTLzwP/9Y0a0xqfH54uHrxqn72byLPBuz+1x+vu3rqpY/hsvACr/ucAb/id+/mt7/jamz2MNdZYY4011njBY53k+CJG/DwLv9f/yNv5W//shZnk9xN/9EkuPgte+XOBt74IhI5PFMM+GT706Wc/A7HGGgDtRLphoS/2dHYpnTI9F8pESKN0nILCbYvDkfJdAmQj1A61sqhaoeuu2+2VdKiCYvigJeQBkoBeaexM/HSjjbhxwA0C5amIrsSHFw3jj9nj6V+hhCjx+10KFUU1XTcvC6R7BlsqoYcsRCCJU7hKbO5Kl5BoT75dEguPnRnKZUrz0TGLOiNERdkmbGQriqRl52DIZLKkcYZ5k2F0IETYKlakxnPruT1OjhdY60kSj+28hfOu+93La1aLjCaI73KWONqgSa10istDEev1bMP2LYdsjFb0ezWnJ/PjLmhiPGdPHjIuKoZpjXeaPHHUVcL2LYfir60901mfxhuxaAMmhXTNTw3mKBU5fds+pyczXn3mEplx7Jc9BknD6eGcs4VQY24bHvD1tz3Ev3f6k0ySkk/ub9NPal578hHuKa5S+oQP75/l6nRAboQS85oTn+YvDR5hqEserbf42OIs79i/h4+tzvLQapvEeL7x1P3cku4TouJd+3fxydkJlk3Kbjngvt3TYhVn5NhVzjLKKhLjec+Dd8j3nsRjChIgnXpnePBwm2EqFJMsccdJnCYJ7Jc9rA44r+lnDffvnaZvazLraZzh1NZUUgHnFr00xMpQrVIu7Eri4/7VEft1j0la8uhig4BikpQMkppbJ4eEqNhIS64uB1zdHXHp8gZpKraBjTfsLvrsd937wrYUtqVeZGgFo+GKwaCSzq6S2SE39rhNJ9Z3+wl6ZgmtJqYyC5Sez7uLAOksJwG9sKhGCZXiairX40FKO0+pW8u8yUmNF3tIYHJ2xqWDkYhxE39sbbhaZcfWgr7VQsmycv0xFuFkaI2IiaOMIbYa/UhOU1twmiSTcz56se/zXqMPumtUR8JCqEbm0BK3m2vJqaFLO3VKbAYbDV0arL2Y4jurTVVqdGkoT4q/fvGpFBYJfprihh5TXT9HZF1gvwihnglJ6Jlu+zo2vTOvn1PXka9541v58IVDjgxn/uQTN9dJ5srsuXdYic8xN+Z/+Bcf/NwrrbHGGmusscYa14V1gf0ihAufH43jeoq4D1yHq8hX/sBbeM33v4V/+FsfPU5t/FwiumeKv/JT7+Sn3/4QAD/11gdv6LbXWGON5xBBus7poymqMiRTQzvxaAfpoSY2GgzXOmhedWKoIAmHXjpQRAi9gFkp1EEqFmNzi1pZFnd6ESQ5RciDJLTNhDMacw9DRzuM+JFHdZzM8mQUnqzTkt5mIrHw6H4rSXZdopsykWbTy5iPgiqcPg7uUCvDqk34+Pkz1KsEnUnHMAaFfdWMECGzjn7SMGtyplXOcCAWdVWTkGrPzqKPVhA6i7O9RY/KWbQWgWFqPT4qLuxOmFcZjbMU/ZrKWeoqYZxVGBXZm/W5Y2ufe++8TGFbpnVBah3TeUEEMuO4vD+i9QYXNInxnH/4JKVLOLkx59KVCSEotnpLJkWF6hILi6RlnFccHvaPxXpaRe7d2uHcYMoXb1xkK1sCcKK/4NWTi3z19sNcrYe4qHn54Aov711hbFc8Vk4ouqCa27J92mh455W7ON2f8brbznMiX/CXz3yCV/Yv0kTLo802v/rAl3NxOeYjF8/y8ekpPnDpVkZJxdiU7Lgh75rezaOHExZNSmIkeGVSSAd65+qIRZ1xdjDl8nxIL2l5xW2XmR30CEOHG8tvld1NWNQpt40Pj2cKVm2K1gFjPfU0J3jF/rRPkbT8B3fcz5n+jKq1HDQ9bh/vMyxqQlScPbsvMypRRL3Rae45vYNVgROnpzx4+QQAdw33GNqaw7ZglFTkpuWg7nFhOWGzWKFNRFkJwFlVKcs6JQThYu+XPZpgsCqQD2tmy5zprCf88FGFajTmSMDYWfKFXpDQpiO7vtrQDruk0yRKOBMQTSTmAbOX4DYcYZ6IuNhG4fy3KZpICBqtI1oHmqkIHk+OFvig2Vv2OLU5Y3c6YPexMbbrROtGSYJrbTB9SWHUjcxWqUKSVtttB7uZaDQUYn/ZdroNIAzkO4tOSbjULCWkEbWbgorEpUVVcl2rUkJ2igtGjoWJtFvumHsdk0gYOHwRiWmgOunR5bVZDeWu/1a3LrBfhHjDb38MeOZ86X/zoYv81l889rTrzCrHg1evL+zll9/9CL/74Ut8amfxjMSU14t/9OaP8+b7LvOe8y9+8d2zbWC/+b7LN2YgwK++99P8vV/90A3b3hprrLHGGmu82LAusF+EeNvHPz/KxN/5l3/B3/mXf/E51/vGH/uTp3ztiVHbAH/5R//48xrP9eAtH3tqr+oXMhoXmFXXHx3/bAki/+PTUECeSTrm+d0l/+A3PsxvfODCsxzRGi9Z6EjcaGjGEbVZ055oIff4ItC8rESVBr3SqMyTXrGoJEjXyUoIRNQRWzjhbPdb2k1PyANmZmAiLh8xkfCa7IpFj1rCwBMz4WPTanEJmTTC2W6FB9qccsdWZUnaddISj0k8oRc6lxHEdSCIraBvZFx60MoYa40uNfMqY/PEDJs59IUcXThsKrzzInHM64xpnXN+dxPntQS5JI5yt0dAHdvVHVQFu4s+1gR2d0YShuI1ZZNQt8Kddc6wnOc0dUKiA71eTYwKowOutYSocFHzyMEGj03HnBtMObExl5wd63jV2ctsDySc5Fx/yh13XmUjW5FZx8tuucqtJw8YJDW9RIJcrAps5Uv6tmEwEj3MueGUWZ1ze2+f23v7JMpz0PTYyFcsmoyRrejphvt3TjG0NUNTsQopn67Eyq+fNLx8cIUr7YgHlqdpnMR/393b4eW9K5xJp4So+djqLL9832t59dlLLNuUW7YOGWclrzp5mS8fP8r5apt37t3Dh66co5811K1lnFVoFcmMY5KVfOldF/jKU4/y2o3z/NXbP8It/UOmdU7aa8lHNWbYyjmqIz5oDuuCL9l8jEWbMcoqCdFZpdxz12X6wwq3n9N6wx35Hn9p8mnOjafslAO2siWpkc5qamRGJRSBOHAkvYaebbi6GDBdFJzdmjJrc24v9ghRcd/+GXbrPqfzOf2kYdGmlC7hzNYUY8TFZTwoGXVd+c18xbnhlDYYUuMY90u2xwtCbZiuCowJqHGDsR5dOAlGOgpH6sKYjq5NyaqPUGuiiTKbM5QAppAF4S4DeqsGp+inDSEqKm9RKtJUltR6Tpw7pHES365VZHuwZFoKv7vYKrG2c+o5I1HnqtbYxJH0WkIRyfbEoo8uyjyaiHKaap6JPiL1xCMLTd1dg2mAcXscLpXdtiA0BjszqEkjLj9WPtvq7gaVeeFhK+S4dNHvtudQHsywJeYBP/YSgmUjzZnr/92+YS4ia6wB8Ob7nt+C99fe/8Io9M7vLrlju3/d6/+X//TPeO/5A86/8Vuew1FdQ+MDZeMp0s+2GPr1Z3AM/+Yvvff4/z5EjH6J5cmv8ayhTKQ3rKlspNevYCjWcy432MQTTzu800LVuHeBdgZzsiVGSCeepjFoHbFnlygVcbYrDsbSMTLdcq0jfliTAipvqVYpatCiHieUMibgvcYYSeeryhSbeLGi2xBKRNtYiu3V8Xp1mVBslMQIq1lOf3uFUpFSQfAKvSn0jCMbuOr2FYOioW4srvMc3tkbcubElBiV2I4B+/M+o9NzplVOuZSp/0FRS6EcNMPJiuUyP056BLCpJ0scpc9Ieg6jA/NpQZGKx/XmZMGFwwnjXslmf8WizoQmYjwnhwty07JX9dnMl4wySRbUKpKblkR7BklNXQ7YLQe4IGNvguGxxZgrVybccmafZZuSak8bNFpFLlVjQlSsXEqIiteeOM/FekyiAufGU87mh5yvtpi7nA9cvoXFPOdvfMmfk+uWNz/2SlLjOT2cc+/oKplumfqCNhjev38btbcM+hW75YBXblxh2ua8/70v429+w9vp6Yb3Lu/gof0tBnnNIG24e7zHHb09Fj5j2haMk5KTyZxct2gV6OmG3qBmnJR8yJxjZz6A1NHrO1aZpG5uFwu2kiUXZyNed/Y8szonG9ScKuacyBfsDec8Nh0z9zm3pf8/e28aK1l6n/f93uWstd66a/ftbXo2zQwp0pRoipYsWRAtwZYlwDYQf8iGwHYS50sSJwoUxRCgJI5jKU4iQ1ZiRgpgR4GVIHFiKJJChw6jlZu4iDOcGc709N59++61nvVd8uGt6RlSpNjkNGfIYf2ABvqeqjrnreVUvef/Pv/nOeL7Nzyfnpxn1qZc6J2yX/aojSbqtAgZGu66ec1aXHJDOh7dOuJ855Qb8xGTNON9g6uM4gWvzDc4qLs81b/Hx+tLXH95m93LR6wP51gviJVFCs9atyBWJnijt+EC6PLgGOMlYhcWdUxRxQwHC+o2QusGn0HbaMhaGII0y3MqsvghaO1wLnw2mzoiig1tbEOSp5X4VqK1RfYdh7MuWdwSK8tmZxGsB+uYUV4ySCtmdYIQnkUTB9/0VqF1SBaNhjVxYmiVw+dB/qEji9wscBsCu4jpbc+pytBYqbTDGhkmyoDKW6pJQr4WGm3b5fNoW0UyWuBcSJ205xxSeEyliUbLUDXhGXQryl6QjhkjcYNwcW2txO9UpGkLaYsxEjUKx3yQPrRXWVWw34a8lbHmX6/++1udF/amAHzqxgn/0j/8KI3541+HTy49yh+0efFhvK7uKxzrg7999YH3ce1ocf//v/iRlfZ9xYoVK1as+HKsJtgrvi4OZ390Eu/ct4cf9Jfjb/zPoZnzP/rfPscnrp1w82TxVR7xtfGrn7j1UPf3MPh7/89Lb/UQVnwLIoQnUhalbbCOW1Zbu50KayVxZMiyhk6vIolDc2CehoptFrd0smD5FUUGKUOYxav/2llMN6spZwmxNiExcC8njVtYJhTm3ZokNggBsbZ0sppYW2Jt8EAUGaoyJo4MSWRw+ylah+pdEhnybk0Wt2jlUEl4nBSeOGnBCdK0JYkMkyqlkzS0k2C711QRQkBjFVsbU7KoJU8bGqPJ45ZeXlHVEcaGCrtz4r7EQAnPfJ4SJy3GhqCaug0L0K1V5P2Kfl4xrRLW10OGwaIOFmrdtCaSIUlymJXM2xgt3XJZP2J/2mPSZEg8c5OQqFDdP5h3qWyEko5JmTLKCjayBWfyKdv5nHdfvomSLiQZKsv53piPH17CeEllNdeOR7x7eJvWK/bLPnfLPu8e3qZyETcXIxYmZqO74C8981lyVXOl2CJWllmV8M7hXc7EEz41uchnxuf5yL3H6cWhwv7E+iHfv32Fpzp7vHd4nb/6Qx9hTS+4Wa/z6RsXSCNDqg3vGd3i0c4hPVWxFc34js49tqIZSjhmNuXZ2TleLrcAeDQ9JNMtbatoW4USnjRtl82fitppemlNplp2OlO0dlRWM4oLMt2SJw2/cfcZJrbDu/IbvHd4A+MlkbTcOFzjYNIlTgzdvMKaYKPoEMyLlFw3PNXZoxvVlDZG4biQnJDrluuTEZGwnO1OSDdLylbTjRvuXt2gNq+9/1J45m1CJC2FiZfvQcS53pjdwQRnJUp6srgNqy5pQzuPSdOWOLZkeYOObEgFjQ1SOrKkIYkMOrLBojFpybKGKDZkvZqmisjSllgb+mkIUDoqctLI0DQ6NM3KZfPhsuLejRt6eZg7NFVEmjUUd7qkSUuSGPh8Dyk9Sjm6eYVODfkyqbST10SRCed63IZKtnKgPL2sJokMdRmF81F60shgjKST1URxeB690YJet6ST11ij0MpSVRFZ3JIl4TjpMrgpz+sQBhWFpM5Yh6bmSD24YcNqgr3i6+JTX+Im8vuvHHH5p36Dz34beyX/p7/2PK8cfm0T6wdNgZyWD677+kq0X0Yf/7XowFesWLFixYoVD8Zqgr3i6+SLq9W/tfSi/vjVt7+jx1fif/y9a1/zY37pdx5MnvEw1gb+zm+8+Ee2Vc0bs0/8h7/1yht6/IpvP5wTNEYF3XIdMy1SpAz/j2PDfJ5SFAnY4x/LAAAgAElEQVTzcc6iSNCRZb5I0doxmWWUdYSUHmMUTaNoGk1VRRSLlHy9YLpI0YllOsspqoRou2ReJCR5SzHOaFtFWca0raJqIuZFyqKMmc0zvBW0rUZpy2KRUlQxYqumqoJOc3LaoVgkzIqEqg7bZvOMokgoTzOSTkO1tMm70D/l8PObRIOaySRHR5bqOMNYSWMU8yZEXgvhWdQx00VKFIUAEWclbaM5OO0xLxJm84wsb6iriCQyTKuU8fVhiKKuNU0dsahjqibCOhHCP07z+5pt4ySTIuP2yZCyibi6t8HeuM+iDVpvKTx35332Zn1ap2ic5vSox6KNOS0yBlmFFhbjJcdVB+Mlxiu0dPTjimFc0liFko7KRAziih+6+BJTk3FzsQbAftEjVw03ihGzNqGnay73jlnTBS8tdtivevSTij934XlS2XJiOpxWOV1ds6hjro1HPDk84MnuPj1V0frQTxJJw14z5A9PdxkN5zy+dsh7RreIhGVuEq6WG9yth5yYDjeqEX84PcfHTy6xV/b53buXeXa2i0VwVHSwRoEXLIqEsgjvSapb9us+zgsUjo5qyOKWLxxtcVB3WUsK1tKSy4Mjfn3/HQA8ld7h0zcuMGsTvvfSNdZ6QadftxFZp2FapDx3dIY/dfEap3VOKlp+eON5dpIJzxbnAHi6u8elwQk3yxGZanl084hIhSJJNKoom4iTRc7hQZ9pk6KF485kwLjOME7yytE60yYlVS1x0mKdwPkQojQrUlSnpSwSimmK90tNNjCbZjSNZjrLaYymqTXOSeo6oixjmjKiPM0YDAqKImEtL5HC8/LeFlJAa9T9GPR5k9wPJOpETYiSLxPaVhOnLbPTHL1R0ZrlOflEQVmEc7OsY0ylmVdJsIGUjvk4p201RRWjIsviNENGLpxPZUKaN5R1sFKczLOwYmQ0dRGFFShtGU86LIqEKDYcTzrhvsvvlWKeUNYxSjmqMvQQTGc5bauoW40x6v7K0YOwanJ8m/Fmpe3927/yab7vsQ1+5a+9j5f2Z8yqr8EccsV9vsH5MV/E1aP5Q9/n3/vnL/Fv/cCjD32/K97GmDB5bOdxcAKoFNGgph2nxGsVfhIjZhK/2WLnEVZ79GFEtd2g78XUQxs8p5fuAjiBHmt87Km3PHYaIzstrtK4kxi5XmNrhVEeWkkzSYiONHbDYCPF8JMJkyeD+0DnuYT5Uw0ysfjjBNtviVKDu53jzlZ4K/Be0pzm+K65nz7JZg0e6kWM3otZO38bLRwbTx+xvzdExhaER5aSeZHQzWvmVYKdR8xbibfB2cSn4XtUR5YkDQmG81mKt5LSx7g6XBRYK4l3CrwXWCtxjWJhgvOISyVNrcn7Fb2sZlYm1EZRVRFn1ycsmmXTWqM5mndQyjFvYhZVTBIZru5tkJ1vGa7POZp3QsNYZDBehUmok5zpTSlNxJ3TAWs7BXeKAXdPBrxr9w4byYJYGhSOz012UMLxHYN9Hu8dcK3YoDAx71y7S1fVKOG4Ww/59MEuWWT4/u0r5KrhE6eXWLQxd08HzHsx5wYTUtVyNh1jveRKscWdYkCum/vyCO8Fjw2POJNO0NLx0nyLFw63MUYx7BZUTUSkLcZKiipmvR8a8j55+yLdS8FxBOFxRiJv5YgLJf1OxWHZZXftNmtpSe0iWh/qklUZ8+zeWd577gbTJuFsx9OPK56vdnlnepsffOwl9so+5/Ix53tjXm42KaoYaxRuHPMnv+t5BlHJdqZ5sTzD93RfoVAxz8/OYJzisXyfrWTO79y5zHt2brObj2mtohdXtKdn2Ll8iBSv/YBUVnN+OOb2ZMC57hilHC9cO8vFc0f084p5lZDFLfmgpG0Vdhwj8vC5NMsL3uksu+8H7ZwIk28nWLQpej+mHVhkJREbdbhIlo7KaATw1O49nr26i05C0aZsNa1VrHcKDqZdBklFGoUGwrqKkcoiCo0RYBqFN5IoDzIdPLSThGhQs5ikYaKc6JCCWWYhXXJ5HCFgXiSY5UWwjC3eLf27JzFy2CAPEuqd8Fq5SuEjASh8qRG5QRzHtF2LPtVUSYJYrxH3EqbDCKE9ZhqH5MtSIjcevMdtNcF+m/Hc3a8eef2w+N0rRwD88H/zmm3f88tmv293HnTi/Pm7D/Z6PYyJ+JdL+Pyl3/3aq+6vxz+U2vqKFStWrFjx9mIlEXmbob4WD5kVbzn3ptUD3e9LJ7JfT3T6l/to/NNP//HBQitWPHR8qFiJJKSxYQW2VYha0syDHVc7tKGSpjxipoMH7kkUbGpzE3x6l368opbY1CFrgS01SI9bRIgq+Pi6RoETIfmtDv7aXhP8fo1k/A4TvKwjR3HWgRW4VuJ7JngAA3Y9VJOpJem1hPyOQsx0qGA3AnEvQdQSeRxhck8sDUdVByE8nbWSODVo7fDrDW0ZYZepiaobeiCirMWXGqUci3GG1pbFNA0e2ZVGRg5vJDQSY4JFWhwb5sd5eE0d6NjgWkV1mhInBuckszKhutVjPsmQMliVzRZpaBq9HdIcrZWcTDvEOlQEh4MFpYnQyjHIKvqdiskiY1qnTBYZWdTSWMUgLpHS8/n9HRqrsFZyNgsFnpuLNT55dJFIWp4Z7JFIQ+00L4636OqarqqZ24Sb5YiXp5tEyvHMaI/CxVwrNmisYlYnPLl1wMXeKZe7xzzaPWJiMq4sNvnws0+xN+3zwsE2r5yu8+KtnZA+mc44bLq8PNvkc3fPspimWCu4d2eN2Tzj+KTLfJHS1ppJkSGAuoh4YbwdFkPasArQbrRwNyVSlrWk4EYx4lL3hLtln+vTdRqjyPOatlXcnI14dHDMmWSC84JPTS7ySrPFE5177OZjGqe5mJ9QVDFRZLG1Ij8zZ9Ym3C6GnM9PGeiSq/UWZ6NT3j+8ykmTc73aoK9Lntm8x17RxzjFo/2j0FA7qtgf94iUxVpJqlo20gW11bzvzE0y1fKOzXs89chdJmWKFJ6yjFHShYbAxCByS5w3+FLTjIMUy7USoR29vCbv1CA8UdZCI7Fdh8gsrmPxSwlTmrZUrWaYBj/0tNuwNZqytrQE7KU11knSuKU0EZEKjZQAzkl8bsJ3gCCct04ill7cqhfuJ8cRzDSmUeh+E9IdnUBISHp1eL+KGKRHxRalHK5W4bm0AlsrbN/gFlGQrkhgFgUv7dzgFxofeXSnxYxafMcg76bYjgue2HdjhBFhtcyH74YHZTXBfpvxk//02bd6CCu+AbxegmOd5xMP2Bz5er7cBPuNWjq21jN5CA2YK1asWLFixduJ1QR7xRviif/kN9/qIXxb8Muvk3L8/Idf4q988GNf8z7kN2h1410/88+/Iftd8TYlciSvpHi7rCZJcLUimgrEXOOXWmURhQqSTxwu87g8NHj5RiK0hzRUsnzkwz4iTxB0CnAgrEDWEm8F8d0IUSh0KcALzJohvR0tx+PxwuOMQHiQuYFSoVODt0HjHO3FWCshdVSP1FSbDt+xy9Q7cJnHpw4XeeTyWng3n1DUMb0sBNaUk5S8WxOlhqbV1K3GW4GOLaYJDXttoxFzRVEk+FJTVzG4IBHTaUi8bMugwa7KGBE54pcz9FGEswoqicyCvtp7KPY7xLuL8JwbzUmREceWqonoPnmKWgaJKOWoW4161d7MhbRI42SwGGw0N65vMuiUdOOaoo2ZtwmDvGRnEJJg333+NidNzkfvXgoNjVFDP65IpOGV+QYf279EHrWcSSfsVQN+/94jfPz2RYTwvGvjDpvxnA9dfYqXJ5sczLt04oYLnZOlptoybnOuzDZ56XiTjZ0piyIJqYaRYWtjylNr97hbDnju8AyfvXYe5wR5r4brIQAsSRuyToOpNZvrM3YHE2Jt2diYUbbhNcWLkAxoJHZksE5yUPQ4m03IZMP18QjrBdODLtZJnJEsmrDq8u7ODZ7p7zFvEz46fpRNPWMYlRxUXUobB328E+SDkjxpOK46fPbmeRYmYU0veLnYYmYztqMxmWp5YbzD2OTsZmMu9445rLtM25TrkxHWKM6sTXFLu8pctwyjkicHBzgvmJkELS0b6RzjJK1VxLG5n/DpvUBGLqQpxo7OZoFSDhU7ut3QQBnOtfC5TEcVyYFCxRYRO3ylkMpRVRFpFD7w0zqll1eMF6GRtypjIumwXhCpYOd4NOnSWoWzAneaoGKHiF/TUttphC/1/a7+dhHjMgc9A/MIM43xRpAMwzmlVEhTFdKTXE0xpcZZGb4DrMB1bEhtBXBBV47w+CQkQEq9/I5JbTjkq+/9VgORQxQq3K49opLIRuCLB1dWrybYK94QzZexflvxjeUPb399Ovtv1AR7xYqvFdPxUIUfbzUPS8Sm60PjoCRESlfhh5PIoRYSIkf3lgg/gguNmEZgBWoh8bHD5Q5hJMKHKHOXWVxu0YcRbT/8qLZDG6LOE0t1xoRl5XH4wZQHCbbjcPMI4QWm0sjTCFcrTD8sOwvpw7bUIxOLaCXRJJxXIgqTbr0QNE6jpaVaxpdL6VnbnNE0ijgxNLc7FJOMNG+QyuGtBOWJn82hb3BHCdGwAuERaRizdxKhPNG9mHqSBn/tyFHtGMxWiz9IELnFtQo7CcvhomuoFzFpt8ZbwXySUZUxbRMi1IsqJkmb4OIyC+4oR5MuZRsFZ5YmYv9ggLeCtZ0pW505p1XG4bTL7fGQtbRkM5vzxPCQtbjkY9cfYaO7wC19j3fSKdeLdSob5AGP9w+ZmoyXJ5v0kpoLo1OGSckwKtmrBox6C04WOVvdOY/1j1iYhDvVkJemWzx/us3nr+wyX6RYJ3jizAHbvTmTIuOZ0T0Sabg5XWNRhosTCPKXi++9TX9jQVNHJFHL4+f32enMONuZ8OTogFFW0BjF+bVxmHxZydbvKUSpsE5yrjtmZlJemW/yfWevUtQxcq54bP2Ibr8k1ob9skcsLN+Z3eJy94jCRNxt1lA4GqcZtxnGKJwTaOVYVMtkwuspX5husaMn1Fbzh4vznJguj+aHXOodc3W2TmljnsjvcSE/5aQOkiApw++uFo5eWnNztsbNYo2DqkuiDIWJ2S/691/3SNn7k+u9gyHOCZK0CemonYZuWt9P/tTK0tSa+X4XlEdph5SO6lJDnLT3pVbWvJYKXJqI40W+dPsIs+NBf8GsjomVve+XvjmYk2hLkrWk28HS1lcKZlHYbyPD590J7DRGpRbZDSmufhl/jhM4JzClpipimGuSToN7ao4+irCNQk01olDI1KAih6gl6DAhDxIU/1pDa7cNk2i7/H2M3P0LCTyY3jKuXYHtWdT8j6YhfyVWE+wVK74BvJnNpg/KmzG//gcfucLzD9i4uWLFihUrVrxdecMTbCHEo0KIfyKE+AkhxM8LIX56uX0khPigEOInhRC/LITYft1jfkII8Z8JIX5BCPHjr9v+biHE/yCE+CkhxH8rhFi5nKz4luQ//ibUwn+pbvvraZT8avzch77Aj/3C7z70/a54G2EFZmSQlSTeC9XgILNw6MzcXx5O9oPMIb8SY9ZCw6HJQLQSr12oQkUO2wtSDWEF2W2F169VukTiQv+UCY/TUxWWj31ojtSZwfZD1Tzsx0Ps8KkN0gztUaca3zHhcZMIr32omFcK0Qiqs8u0OiuQiaUZeAoTc2uxRieryaOGtlV0k4Z2EeM9qDMFUd7gnMS8WgnUjuLCsulLgbMqyBWWF8am0jCLkM1y/JnBGgmJC9ZkowbvBEI51KDFNAqpw21aW2TkiLMWWypso1gsUrp5hVwm/AnlacqI9jBj/+aING1JI8PZ7THdXoX3gkUb471gvbegm9YcFR0y1bIwMXtln92NMZvpnHeM7nGpc8zNxdr9qusgqYil4epsncpoBnGJlo6tZMadcsgr0w2U8FxeP+Z8Z0wkLf/v89/BftHj1niIEp7exoKLWyf8ia07XO4e8Xj/kPeevUlH11ydb3A6y1HKEa9VPLFzyONbh6wlBY+OjnjnuTtcHJwySEpiZZg0KYWJGCYlZ/tTct2ERlLg8H0Oui1nelMcgsOqy2Y6Zz1a8OTGAX69YTOd82fOXeGR/glKOJ4rz2ERvKd7g0FccaMahbdV2NDweiujrfV9//REGX7ohz8TTgkkP77xWTLV8tziHLXXPJnvc74z5uXpJrWLeCzfp2hjnlm/hzWSSZmyaGNaq+jGNdM6pbIRsTSkKjQVFiamrINU48LolF5cs705obNctdDKkSahhyaNDOXSF/785ilnLx3RXSuIIkMxzlj7ZPCfF1GwtAypp5ZYWaTw7PRnHB32yJZJiLEOVfNYWk5mHRzifjOkXTbqegeiCc2OWAFrTVhFqBTCinCuaHvfOjA5VkECVUZEebDi9B2DaZfn0PkSpMduNEFaVodVg+RYgfQI4WEWhefQSHwjiRNDtB+BCPIwmVjssjEaGSrnRC5U0K0I3xcPyMOYwI6AX/Xe/zMAIcTzQohfB/468GHv/f8qhPgx4L8C/lUhxPuAH/Te/3khRAQ8L4T4bWAC/ArwAe/9PSHE3wP+deCXH8IYV6x4U6nahy+duX1acG4tZ/8BnUe+lNp88ZjGxTemOdG6lXXfihUrVqz49uYNV7C99598dXL9un0ugB8FPrrc9nvLvwH+wqvbvfct8ALw/cBlIPPe3/syj/kihBD/phDiD4QQf3B4ePhGn8KKFd8SfN/f/QiL2tCYbz7d+5WDLw6x+czN07doJCu++QkaaJc4mrMNshZQy1A9BtRChkpR4hELTXnGBg2l8BS7Di99CJpZok81tAKvHcWlFtHI+xVtbwQmdzgNPrOY9RZsaFTy3WUlyguIXdCbzlWopMnQOClbESrbRqKW9/eZCxWwVuISB45Qda+DxZjvGWqj6ccVdasZJsHOrrGKfFhSFTHeSaJlsqNrg/0erQzj8OATi51FuEVohPSlhloiK0G9ZUB5vAkNnAiPq1VovjIC3yjccYxbRCF0RzoW8xR5O6WpQqXOlwq5bHZb3OlRNhFp3oSmwH7LaHdMMU+oWk2iDWUZMxnnnBYZo6xgmJbsdGZs5Av2yx4vHG6zN+vxzrW7bKUzpHCM24y78wGpMuzmYx7rHfLSdAvrJM+s3+ORzjGXu0ecNB2uTUcsmphL/WMudY7Zr3rcXKyxuT25H6Yzr2Oe3tznQucULS2ljWldqFzeXIx44fYOUnoGnZJHt47oR6EQEZInFc5LFm3CvUWf65MRn712nufunmG/6JGqFuMV6nQZUBK78Dp6wbxNAKjda9pboTyTNmU9WnApP0ZLx61qjU8tHmGoCt7Vu8WdYsjY5LxrcIetbIY/XyIkOCuR0rORLuiomg9svci1epOhKnh/9wpnkzHXinUA3tu/xvdsXGOvGVDYhB/YfplRtGBzfcYwL5mUKak25LrhyeE+Z7IpV2abxNKSRw211Ty6eYQQnrW0oBvVbOYLNjtzsrgliQyxtgjhmRXheZ5bD2F1g6RivVNwYTjmsUv7xD8Wgm18uWx8TFuMUbRWcftkiBKOzqDCWMmiSDg47iOEp1m+bi/ubVGaiCxq0ZFldpqHz23XBPmiCwFLy6+IsGJEkDYK5VG5odoJjZrUCrVcxYpSg5lHmDZYJ/pSIeY6fGcYiWsl5skCmViMUfjMoqJXGx+DntvmyxCahQ5BNLXEGxHuO1u+71bgEwvRgxeQHqoGWwjxF4EPee9fBLaA2fKmKbC2lHy8fvurt239Mdv/CN77D3rvv9t7/92bm5sP8yl8SzOvV2mKb3d+5tc+z5fJi/m6MA+x0vyB//q3vujvv/iLv//Q9r3ibYYn/DhmNjgHrJkg6QBMrbAdh1ceryA+kfjY46VHnMYIGybOaqzxmUOfRJiBhcSFH77oVbmJxevgle11mJDLyIaJcOKQdZjQmvnSScQI0A7ZiuBnHYWJriqWUpNK4n2QmqAdvpWofhscSJbHRIYYarl0RTBO4r2gp2sGnZKDoz5JZOj0KkytKOehkdHXClktvYCtQMQOoT2iEaR7oZFTjxWyltiOQxXBq5hX/XhduEARZtkA2gqEDc9H9RvaaZg4ucTjF5oob8MFBDCd5fgsjDfSliRqyTp18Cg2wQmiNjpMfAQo6RklBXI5caqt5s5kEBrk8pJIWI7qLr9/5xFemWxwNO5yLh+jhGdhEl68uUM3rhlFC1qvuFf12Sv6NEaz2ZnT1zWljTlYdHnxzg7zMuHeuMeF0SlJZOjpmoWNuTrb4NMHu/zBvfN88u4FbozX2BzNGPUWbOdz+nHFSZ1z9Xid6/fWuXK4wZXjDV66uc3t/TUO7w2Is5Z2mnDrcI2DosedaT94PS+dJfJrEVJ4UtXSjyqmTYZDcHs2JIoNLxxuc7ceMNAFwzhIH24Va9xq1tnUM6Tw3Ct7RMKyGc/pd0u8D/KIflZRWc0XZtts6BlHbZeX6x1Gas7T2R36uuZKuUUsDE+ldzlpcq6VGwCM2xwhPFJ4NroLunHNVjpnGJVczI6ZNwmNU4ySgrWk4HL3iJufP0O1lIykaikJ0UESoqRjO5+jtcMYxVpScPd0wLROcV5QW00kLWe7EwZZFT6nC41zgrVewbRKyJKGkzJHSsfpfh9Ta1ytaIxmXGTEkWHUL9AiJD+2jQ6T6qWbCZMIJJhWBe95AaoSuEbRTBJ8K0mz5n56azIqsTbIp6yRS19sj7HhPPIdG1x+AJVYlLYo7dDaQiNxTiBSix7rkISaOlyjkKUKyaxLj3w82NwR340RS9cioR+8wPXQJthCiB8EfhD495ebDoDe8v994NR7b75k+6u3Hfwx21c8IL/0O1ff6iGseADcG5jYzirD1cPFQxnHX/ngR7/6nd4AL6xSPVesWLFixbcpD2WCLYT4UeBHgH8X2BFCvB/4deD9y7t87/JvgP/r1e3LivbTwG8DV4FSCLHzZR6z4gH4BvSsrXjIXD2cc/mnfuPrfvxvPnfvq9/pgcfycCbqr/KPP3r9i/7+cz//Ow91/yveJghwNvjN+iZUiRi2wVpLcF/+IVuoNyxEwatXGHDrLT6z2JEBBzZ16KlCxpbkVhzkFalFVAqWHr9yWcV2rQrbrcCrYNOV3o4gseTXI4T06Plry9K0kmbDBi/trgnLx5sNej8OVW5lX3tKrUA0Ag4SvBU0LsgLLm8c09Ehze7c9ilCePK4Jc5bVOQwjUYsE+dEKUnu6dDkONP4jqU62yK0x+1WYcyRw64ZfL1ctnavymvAKx+Ws5c2hzo3YbFLedxCw2ZN/8yMTl4jUhssB6VjY3uKc4KyCtX8uo6YTHLSXk0nr7m7PyRLGgaDgkfXjhg3GSdlHpb7dcuTGwd8185tHu8fcqMY8fHrl8jiljxq+YHLV2i95DNHu3z09iXO7ZxyJpuyVw347PE5PvnyJaTwnO+f8ljvkCuzDV6ebFI0EUnacHnjmPPrY7pRzZnOlMOqy/XJiKt7G0ymHRZljDFBkjCvErbzGZMmZb/o8YXrZ6jKGNdKymnK4iQLPtd1sOCrFzEidthCc/vlLdLIoPrNfbu4csdinGQ9WZAoQ+MUN8sRo6ygrTXzk5z/79rjHDR93tW/hVlKIX7z4BnutkMud0Pq4kHbo6trtHIkL2REiaG1isZpZk3CxObsJqfsNQMOTZ+RmvOB4eeJpeFGvYFF8iOjzzOKF7yy2GSv7FM1EdMq5Wje4XDR5aDqctJ0aL3ivRs3OK46aGkpTMx6tOBHv+9TSBEqr5WN+MJnLzCvY8oiYVaGivcgLxl0SmZNyuNbhyTaUBnN8SLntMooTEw3romGFfGxpKkjUm3opTVlHVM2Ibkx6jYMR3O2z4yJtSFPGorlcQCODvskaRsq1w5cqWHQBknX0goT6XGRR2hHfi0i6jaUizh8F0CQDZmlR/VJguy04AVVEdO5GqFSg4wt8VFIdGzKiHac4L0gmihcrZCRw6y3RJENj6+WleyuDTIx8erKlKcdBt/seF+H8T0gb7jJUQjxXcD/AvwB8BGgA/wD4KeAvyuEeAJ4FPgPwwvjPy6E+IgQ4r8A1oC/6b0fL/f1rwB/WwhxA1DAP3qj41ux4puJT914+2qTf/qfff6tHsKKFStWrFjxTcEbnmB77z8FdL/CzX/9Kzzm577C9s8Cf/WNjmnFihUrVnyT4kIFSi4UqhC06waZBbs9IX0IhDhVtBsGUapQudU+NBt6UJnB76e4YYucaszQQKNohi5oqWOHbMHaYNPnBm1oijqOgoVXRKhMxY524MALivMGjAwJjdrjPSQHivqMwXlHtBfT7rT4RuLOVTCJQ5V7qQl1HXvfOs8bybxO2MzmaNmgcJzvn3JUdnFO0gJSerx3+DJCtgK32cBC0wz8smEz2KGJaYyTHqGBfosAfCuRhcINgrWer0MIjygVtmsRjcDnIZnOTmNkt8UJRZK2ZHHLvEpI8pa2VfQ6FY1RVHe6dC+GZEMpPKP1GdYJ+mnNMC/JdIvzgspEzJsE4yRb+YyTqsOZYfD8L23ECwfbXNg6CQEocYWWlpcmoZVKSs+F3ikLE/Op2+fp5hW7Z06ZNzFP9g8wXnFnMqCuNaaKuHD2mFS1SOGZtwmTOsVYxdFhLzS2HaXo7QJrFFFsuDQ64ajsclpklK/0oeNQnQb/aj/bIkIWErFd42IBjULMFGqnwhA0yWnaYl/KqXaDTnneJMzilCe7+wDcnK/RiRo6vYo0MhxdG3Hr3BoXkhPOZae8PN9iO5vxqclFnure40TnPHt6lmeGexwd9dDvnGNbxXiWca43ZhBXvLA4w4+NPsP/XX4nN5oNKh+xq095b/caHz59msLFfFfnGk9ld/nE0UUg6PuTyJDFLScvrLP93TP2yoj9qsef3XiBl6MtKhuSOI/bYKW4mc45rLo4Lxk+dkInbmlMmAIeLrr004qjeQclHYOkJNcN1klmLsZYxd60j3WSdh6TPT3DzRMqo0MVO6+IldkkvMQAACAASURBVEVLh6k13VEDgJLBJtNZQRq3TJsE30jypKFpFN3PZ0y/u8IXmmgmcecbbK1CaNNGg44N5VlLJEPgjVAe10raoyw0O+sQIBXFNmipW02xa4mUozUac7EKqzgCyCxSeky2bKZWDmsEYhkuhCDorKWHIoZhc7/vw/ZDVbvZtHwNBexV0Mzbhc/dHnP16OEu+a94+Ii3OE3xw8/vv6XHX7Hi1SZdlzrarRZRy/tSBl8rhHLYjgvNfp7g8tFKZG4QM41rZYhPXrp9qKVHtTQEFw4jsctYdTGOULFDlhLbN+GHUvvw2FqFv1uBGjSIhUJYQrLbQRLkKVYwfE7TbreoJLiJANBraYqln65aNlHmBqnCvoXwTOqM0zqn9QrjFZXRLIqEYVZhTXARiQY16fkZKrbEm0WIcl86mgjh8Wstcq7x4zhIOpZjd4MWsdBEiUH2wv/FsEFPFD4NFw12HuQvWd4gY0tVxMyrhGKe0DYapVyI1R7n5OdnaOkYz3OUdqTacHrcY1olJMowrVMOFx1uToakuuXy4Ji1uGSULpi1KVemmzx3dIYnNw+40D3lQveUtbjkynSTxipSbTg3DN7We0WfZh6HCZ5VPDo45qjp8Mp0g2gpu3n8/D79pOLOfMC1kxFX9oL7yPFJF8oQ033m8UM6WU2StlzeOCaWJkyuyxi5WyIriWmWbhOALCRs1USxQSeG7d1Tdp4+wJQanCCSlmKaUp1tkXOF7oSLirlJeKXYYDcd81j/EOMkzkkWVczwwhiJ57nFWXbjUy53jrg5X6MyEcdth8LE3Jv0uFsOiFKDsyokhb7qbe4ln9o/R+s1P772GXJZ87niPNfbDXb1KT+y9hwzk/K54gKRsHz/1hXeM7qFEJ5eUpNqw/Y7DqhtmChvpzOOTJc/s/EFvmd4jcd6Rzx7epZbxRpdVZMqw7jOiJTj7tGQYV6GCHcPt4+H7PRmrGcFd+cDTqucYVKy2QmuI4+snTDMS/obC7KkQact+7fXOJh26SU1WjqO5h3W1mfLizFNN2qojebCzglpZDg87dHZKCjqGHerw+RdTZCICU+72Qaf6qXntZA+yECcwFmJ8wK7iMJFZRTSFTvrBcmoxFkZPOOXF1PeA7MIFVn8OKRm+jo0N/qeIcpb2jJIoowJkiwSh1AObwV6uwiPiTy2bxGJDee69OE4D8gqyOVtwo//wu+91UNY8S3AT/0fz/KBp7e/+h1XfFshhPgA8JcIjeXee/8zX3J7SsgyuAM8DvyX3vuXlrd9D/BnCT9vPwj8G977W2/i8FesWLHim47VBHvFijeRt7Z+DVVrv/qdVnxbIYTIgf8eeMZ7Xwsh/nchxA957//F6+727wE3vfc/K4R4JyEA7E8LIfrAT3jv//JyX/8EOPnSY3zxAYOXrqglPnKItQZTK2hFqAYL7le1XBbs4YgcfhyjConJFKIVeC+xozYs2XqBl6/tX9hlY2NukQ7cwBAdRLTrSy/r3KJPNGargVIFP2kJLncII2GjQR7F+I2GyZ+0UClsI5GlhC6hyVC7UB3VDrOIcKXGWUE0VnQuBg/i40XOdw7vsJ3OOJePud0dAjAaLHBecHgyRK+VRLEhiQzi6ROms5woNlTjFJkaXOpI10vqezl+0KK6hl63xK4JZqc5/bWCUjuE9LQdFyr0QJSHtD5jZKiADxqECJXxLA8Vx7rV6MTQTWvmVYI1MqTi9UGnLfMiRUnPZJ6htaWfV8HXW3hmJjStXRlvcHzSJb6SsfMXbtI6xaRNmTYp4zJls7NgmJRo4XjxdItZmfLkI3sMk2BtN21TXj7YJIoM/bRmqztHCs+0TpkWKUKAO46pOpo4bdnYGjNMy+Bd7RTGS2JpuD0bUpYx7jRBrNX0L49xXpDFLWUT0WYtkbZoFRIGtXREyrK5M2E8zYPHswn2bT5ZWhcqy6XOMZGwOB++vffnXfKk4Ym1Q/bLHodVl8YpJnnGRjTjcu+Y0kYc1D2k8PSymkmT0VYaXyn0RKE2HGezKbeLIX9i6w5fqM7wfd0v8M70FpWPuFZvEgnL+eiY7+2/zD++/X7UhqOrKg6bHqM8vHatk1RNxHY+Yyeb8Vh2wF4zYKBKclnzZH6Pvi753GQXLS1aWkbpgv2ix8baDA8spilyUDLolkybhG0dVhaMS5k2CVUTMcgq0nRBog0HZY8sa7BG0d0Mq+ZaOCqnMUay2as5XuREyjKpU6pWc6Y35dZ4yPZoSlHHzBYpYreEeYQ8SbA9S7SvMbshYVFlBrOIEKVEb5W0lUYoj0wNOrK0iUCchMq0NQpPsMhMBzVtpjHHGT61mCY0ULpKoSeaOo+gkbRCI7XDe4VdpkDKyOIqHZqjCee48ATJltXB+lJ4vHvwafNKIrJixZuAc55/9PvXqcxbO8H1wK2TgmdvT96U4xXNypv9W4D3Aze89/Xy7y8X8nU/OMx7/yzwruXk+s8DcyHE3xRC/DTwHu/9H9GqvT4czM5XUrYVK1a8/VlVsFeseBP4737rFX7uQ19g1Inf0nHMKsOf/tmPvGnHuzuueGzrK/VAr/gm4UFCvr7SfS4C7wP+GmCBjwghjr33X/Qh895/EPggQHLpnI+ONabvUKcaOwJ9FGFTh4+XIkoBvlFBi1wovACfOsRChqquje5XmtwycMVljmg/pu1bvPKISqILib/Q4kpBu9GGfWUOOVs2T7pl5brSJCeS+nxDfDOmPt/gezYU08tgB4b2uNQhTmOGLyjG7zSYRhL1G1RusLMIIkc7hFiG6t18nKEvBa3zdjylo2penm1xeXDMtE2JzlsOTvo4KyiPMy5dPqCoYgadkqbW5J2aeRH00p1zs9CYmNco6ZiVCVFq8EBbRIhKIddr0rTFOUE1T4jzBucE6c6CSFvypKFtFYtJRndYYK2k2wmJk1UVMegVnF5bo92UDLoVZRNR1DF52pBEhkf6Jxgv2Sv7nCxyRp2CVBse3z2g/0jFUd3hznxAaxV1q8mTho10wbRNMU4yrxI2e3M20gWV1RQmZn/eJY2D/rafhPTFK/c2QyXdCVQcQkOKRcojO0dEMhQpChO+S50XHBUD5mWClI61i6dkUUseNcybhEUdE+tl06cLn5VFkTAjI05aOmlDr1sGHbMEfTvBnq9wTjCIK0ob46ThpO3QUc197XhH1zzZL5mahHGT8+H9p3jv+g3e3bvJ1XKTG8WIeZvw1Gif0kZcqXcQrcSdrfBecFB3cQgeyY84NTnPV7u8N7vGn8pf5pPlZV4ozxIJw64+5V/e/Ri/cfyd9HTNXtlHSUfZRijh6aU1uW7RwhIJy141YNzmnE3HJMKwEc15ZrDHJ44u8sQgRIucqpzKC2ZVgm8UWdyipeN41sFYxXq+IFaWg0U36PTrmONFziALY6/qiDRriJarAQ6BEp4ospRttFwdcLRW0jRhmtlLa/pJxaxKsIuIfFRgT5LQ4GsFLlL4MlSKhQwpjXgRVhsSi5COtojx2iG1x603LI5zRCmR6w1+ufriXUjiVKkNDZMyNAzbrea+9l0IcCbYY3oXAmuE8ojE4q2gncehgXL5WcPIEHbVeZ1F5gOwqmCvWPEm8HMf+gIAJ4vmLR7Jm83KnP1bgAcJ+fpK95kCn/Het957R6hy/8A3cKwrVqxY8S3BqoK9YsU3iI++csz7H11/q4fxluI8/MrHbvCX33OOLH7wK/8VbyofBS4KIZKlTOR7gV8UQowA472f8lpw2O8sNdh/6L2fCiE+Avxrr9vXReDXvtoB2502BMXEgvRmTLVt7keFA/er0xgZXDGER8QOnMZbGezwahXcM0Y1fhrhu4Z25IO2O7fQatp1g/LLqPPU4ZchEq5nQ0umEyG8opWYjkcIqM8YKBVq0GKrEGPuOhaZGuRJit1umD4h7mudTa1hHlwIXtWLAxy8sk52ZkHtNLXTtF6xm5wSCcvNckRtNdv5jDxq7zt1aOm4uH5KbTU7G0HGNbhY4YFZlbA7mnA471BVKUlieGznkGmdkmxbnIdhVtFaxdGsQ29YYJ1kmAfN9MGkG6q4RtEZlHgv6OYVk1nOoFfQyWuU9PjUIYVHK0s3dXTiBi1ccJtAcG28jhCe7d6MykTsdKZ0dIP1go9df4QkbbE2xMQ/tbnPvE148e42UjmS2LCZzTmqOpyUOYf3BuzunmC9YDNfcGs8RC6t3nTakqYts5MOmzuT+6/TUdFhXgX9d1VF5HlN02g6Wc3u5pRhXGCcYq/oc7rIKE7ysOphJGKukes1rpV4K9Ev5oyfntPNa4o2QiWWdkMgThJYazBecnO+xmY2J5KWjg4qqkFScVh12clmbMZzpk1GpluuF+v0VMWT+T2mJmPSZHRUeG1kbiADN4+oreTOfMB6VtB6xePZPp+bn2eoCp5O9vie7BU+ySN8rrjAO7LbrOs5j3UOeX66w0v3NunmIbhmPM3vB5/0RxW3mzW+f+0lPjc/z8RkfOjqU/zQpZfo65Lz3VOMUyjhsU6ylpbBmjAytEuXjm5W04kbjosOZ3pTdjozqlRjvaQ2muN5Tpo1GKNI45Ze0lC0UXBbqWOyuGVapKx1C+7eXOfipUNGeUksDbMqoZ9U9NKazrmGaZHiOwYdW+xRgos9stsi9hOsUejcYCS4gxS5VS3DnwStCHrsKDE0VuC7Hr+foLZrzCIKVp2pxfugqxbLMrKtJHFukLcz2p7CbDWItVDwcrnFGRlWq5QPrkW1xPVMsAxcxqZ7I1HjlQZ7xYq3nI9ePX6rh/CW8y9eOOBv/Z/P8Xd+84W3eigrvgLe+wL4G8DfF0L858Dnlg2OPwn8O8u7/TxhEv63gP+AZV6B9/5F4H8SQvysEOJvA3vAr37Vgy4n0iJ2wRat1wYP2uWkVSYW2uDvjAzWdL6RmLMNvlpeqC1lG1J5fBqaIVXH4P9/9t48XLbrLO/8rbX2vGs6deZz77n36kq6uhosyRpsjA22wcTM9BMDAUK6O00HCGASyNA2TYcACXTSnfTjDuGxaeiH0AQMIWAcm8l2EhvPgyzJmqV7dcczDzXvca3Vf6yjY10s2VKwrGtcv7+qdu2q2qdO7aqvvvW975toVKSxoUGEGimNEygZgYpqsOCl7vlEJg+LbJ0avKhCJbVbphYWMT4YJVEWUyrqucqJLxPtrAHjGkYe1rOopIZSIgfuCzhaHiOEZStvcm26zbnJLMZKjoW71FbS9HPmoxGpV9INx3SjCbFXoaShG43Z2muxN0zpxhMWkyGdOGdr2GC5OeT2o5e5eWEDKSxHmz2WmwOOt/fxhGGz16SdZqx2epzoOr1pqd1rFvk1SVLQiArasRvH0JlHK3JjJ5MiIJmduN8J0o22hKrGIOgXEReHHTpxxkpjwFw0pjaS2ki28waP7C0ShDUrrQEn53a5YWGLXhGzMW6CcJZrx2f22c1THn1ymd3HZ5lbHOBJw2rTCRIHwxjA/QAwktl0wtzCgEBpfKUZlSE7+02UNORZgOdpIr9G14pWVHCysYOxklEdsjdOKPKA1vwIawRhWhIuTZAHCX1pJ6NY0IRhTW+vQW+UoDOFqCQ20tiJR6UVK2mfbjBGHqzGLaUDait5fHeeT+8cASA4SHo8N+jyBxdvozA+p9INUq9kp3Q+1GbiESUl4WxG2s5ohzm1kVzKZjgVbHBjukZPJ9ybH0VhuTt+kjl/yHv2b+ZcOc+iP2A+GvE1J846OztgfmbIYmdIIyj44OVrODOaY79Ouav5JNdG27zh+ns5N+6yXrRZDIcUxmM7b5BVPoMiIvYqmmFBXvrsbLcoa0XkOVHo1rjBsAqZVAG1kTSCgiR040e+X1NUPhs997+otKI2ksSv8DxNpRXd5T6XtmfwpaY0Hv1zHXp5fCj0n2ymqFCjK4k4sM8T0qLTg4IWEEN3bglp0FqCFa7QNu78JFMgLGplgh57iFA7y82Jh9UCP6zRhdtHBm7cI78+x6zkBJdd8qtSxo2OTTzw3XtDJDW2U7mU1ANk6S7rbvUFP96eYtrBnjLlhWKaXc/bPnAGgI1+/iIfyZTPh7X2PcB7/sK2f/y0yxnwo89y319+YY9uypQpU778mHawp0yZ8oLRm7hf++95eJP7L/Ve5KOZclUgQBx0k2wtUH3X57EW1zHOFNa6ZV4V16i+h3ewLGuNINhVTmhkwEYaz9dgBWrfw1qIzgdIaZy139jDGEmwL/F6ynXACkldKKwR2MCNlIinrLkORHC2UaNrSdCTWP8gVTFzXWCxFyDjGhFrTCURndKlJx78nrazzg5PKUPo1yxETht6V/scD4+XGZqIr5l5nNfOPsZ8MGJYhTy2v8D1zS2OJj06QUbDL/i66x6lmeQ8eGGZ2XDCidYuN8xtcevMZWaCCakq2Ro3KLViUESMq5CtUYOXrKxx59wlluPBYRLiSqPPHUcucdvcGnFQkfgVjaBgOIrpzI2otGJ/s4UQlqpShF7tOr24lL+1XgtrBaM8pOnnBKqmtpJuPOHSsMOZ7Tm0Edy+dJn5eETLz914xd4MZa04tbTNnccvUBvJII9QkebIjZt04oyjjR6TOmBr3ODIfA9fGZZaQ1567CIXt2fISp+N3TZ7k5i9Scx8d8B4EjLTHtNKc+aSMTesbPLK+bOM65BBFXF50AKcAHYmyRDKstAeoZRBKoOtJL7SREtjqkqhAk11YNdG6v63ItJc29phv0hYjfbItM+Z0RxtP8eXmnacM8wizk+6rMb7ALTCnJVGn/tHR+mqMS/tXGQ/T9jMWgTtAnPw/oqDikBqEq/k3KiLRnB3fJaOmvBItsL9xREUlq+Kz3BH6zz3Do+xWbWYD5yF4XAc4SvNpAjoRBmDIuLupYu8pLWGFAZtJU2VcTTY4+b2Og/sLLNZNDFWHI77AOxMUnpZhFKGxcUeZeUxLJ0QVUnD+c1ZtgcNLu+22c9j0sCJXavKIw4qTi1uo4RlfxKT5z5bgwZJUFFryd5mi+OLuxTaI6t9rr/lEqFX40nDxvlZN4KVee487Jaum10oVLNC+sYFAHkWmhXVKMDshe6cz9z/SymDyiRi6BFFFTJ2Fn469wjmJ1gjKPZiyOVBFxuKXoQXurGUarXAFIpq7GPTGpHUrtM98JCexR501qVnELXAJBo/rp6XrGhaYE+Z8gKxPSqx0y424IqnaRjSlClTpkz5SmE6IjJlygvEb3/8AluDnL/1iuMv9qFcNVhrX/S4+ClXAdbZ42FBt2pELZH7PjawxBd8shMg4xprBKal8Xc9N3NdCcqVEtnzMe0a4Rl0LSHUyH1FVUmKOY0dBk6s5Fn02MMsaBevPPTBs4fR4gawRrm50MBg1yLMfIk8EDbVMZ9NhzoIwLHd0tmH5QqZVghpsZ0KqwWiFMimRQpLXSsaUUEoa9byDn7sRHKf6J3gO+bvZagjrgm3OZfMcq7uciLa4ffXXsrXzj/BWtFmPhjx6uUnWJ9ps5k3WY77LEcDAPpVTKkVX7V4jkwHBEqTqpJbZy6TqBJtJSMdUltJu50zF46ojaSyitiv8KVmWIacWt5iXAVuDvrYDpVxnd1Q1e7+WjoLN6WJvJoT7T3XhS4jhmXITJThK81ie8hSOjiMQtdWsjtOUMpwy/w6vjCEquaT54+hc49Xnn6Clp8jsWTaZzdLSPyKldQJO+fCEXtlymJ3QOTVDIKI0KvpJhmpVzKfjDmR7rJTNNjNU17SvURT5dwzWcVYQSsqyGsPOqCkQUqLsQIpDUUvIZmdsNwaoI3kUq+NEJAPQ0RwMP+bK/x2QaoK5qMRW2WLI7FbgdspG4chOZt7LSZ1wF6VcsfMRR7or1BbxX07K9yYrtP2JsxGY3bz1B2DEVQ7MbKRcSzdozAe1zZ2eCg/yh3xk9wUrgNwvpxjYkLuiM/xkugiO1WTx8cLSGHYyRt4nmGQRUhhyWqfGzpbjHVA25twMe+yJVq0vYxQVrRVxo2zG1wczbDa2CfxShbSEeMqYFL65KXvVozCknwQsmMEK10nKp3vDgiVZlwGbG52CNOSZpI7S8UoJ5A12grSsGQyDqkmAVpLuq0xfqOkHWRcGnYYTiJuXlqnNm7G+2I6QxiVZHsNbKPGD2uq3HOfC8LpHTiYhaeSqFijjUCU0gkjfU1VeuiO01RMxhF+WFNXHlGzwBhn7Wd8gxCgC4UZuxnrp1YRhLSQH2gsMC4KfehjOhVMPJAW2S3QuYdo1FA7+z6VPPdsh2mBPWXKC8j7HtnifY/8Rcezr1x+6T8/wRu//voX+zCmXAVI/2BMJAtQPQ+dGtCCsmuc+DA62FFZtypbHwgVA4PuVHhbAXVbY5pOBFmnBukbTOD8rdVQoTsHLgC+e2x/28P41iXH+ZqqH2CldSMnWmDmKmwtsRWonodJDtxM+j603RevraUbK5EWqyV+WFJp56VrQoOeuK/VbnPM7iClNxuTaZ+P75/gld0zzPkjzhdznJnMc0frPDc11jkWOzHicuIK6P0ycR7HXs5iOKDjZ2zkTRqqoDA+Ta/ADzQLwRBfaPp1TGUVC8GArbLFg/1lXt49RyJLNJJElnxqcIxA1qR+ibGCW7rrlMZjUMxxJO0jheHTG0fdD4NuQaE9FhojEq+k4ReUxiOQNecH8zSCknaY0w3HLEZDFkN33P95/RQAnSgjCSpunT1Px5twf/8IgaxpNyfccHybE4lLO9yrUsZ1wHI6YFhFnEh2CWXNdtnkwnAGgJlwwrgM2P3oEjd//WO0ffeatL2MWX/MKA6JZMXlosOlfpvQ03TijForXrKwTuoVHEl7PN6b59TsNt78pnv/YemVMZ4y1MDiUo/NC10ncCslxjhnjdQrOD/pEqkKXxjGdXDoANJIcy712wyKiGtXtnlp5yIf3LmWrPQ5m80zHww5kewyqkP8g9EKG2mUdO+r0ngcC3fZqlrcmx/nlfETXB9sMjYhezrlnuwEN0WXuSs9SyQr3r9zPdpIGnHB9laL+YUBu+OE2WiMJwyXixk8adgrUy5nHQZVxHw0IlYVp9pb7BYpAOMqQApLO86Jg4rNBxcYXmNodCdEfs3lnQ7tZkbsV26sRGlmZocMRzGjLEQpw9awQaWdK4nv1TQaOaNRxHzbjbEszbjRKH0gihxVIdpKpDCcWN7lwlbXedsPPWrfYLWEUhKcTSi6BuZKlGecw4hvnCd+uyQIXcqpCDTCN0jPoHOPOCnQtaKu1EEyrHSC1bRGRTXWF5hCOW/ssQfNCtEpsQMfjHBpj2NJHQkneoycDz6lRDYrdOVElKZ+7g2i6YjIlClTvmT8q/c89ozbR0XNnzyw8UV/Pmstf3jvZWptvuiPPWXKlClTpjwb0wL7KqWoNb/2wSenhcGUrwj+4e/exw//5qe+6BHu77j3Mn/v7ffyax988ov6uFP+2xHSYguJVAcWe4GhnqucHddsgY4Nols6X1ojUKGmnqmdhVakEZcjqCX1XIVsVEjlLPpoV0hpEZVbZtapQXgGqaxbDpZQdTQsFy5RTx98/Unr7ADFZ41/hGfRbY0NDDKtsLFGeQbVrEBa1xGXIPZ9hACxFWKtQIQGLBTaQwDFMOTR3iIdP+NEuku/jg/HN0431rlQzDLSISMdslM1ORL3eHS0SNvP2cobrOct9qqUUFYcTXo82F+m409oeRnzwZCdqkFufDQSKSwbRZvHhwucaOxRWYUvNVtFk7WiTSBrmn7BYjTkVGuL+WDEdt7AVxpfanxhSMOS+daIQGpmwgkAM0FGyyvoFTFbWZN2mNP0c1pBTm0UzQPR36COmZQ+C6nres/FYzqe83kOZM3mpElR+awm+xTGYz1v85ELJ/CEYS9POZr2kMIy0iGXJh2yyifyaoZlRDvMsTcNWTjoxgLs1SmDOqIwHmfG8zzaXyTPfYSwzEcjXrPyOMfiPTp+xnww4vrONm0/p3ngZb1XJGwMm7Tj3CVkhgXJ/PjQBtIP3ChApn2CA6u5c6MuK3GfI40+LT9nsTnEk4ZhHvLAcAUlDK+df4zXrj7OWAc8Olo8FIsCzvrRN2xstymM52zwTEC/jvlI71oeKZfIrceJYJvC+HxicA0P5UfQVtJQOavpPkJYtBGcXN1mIR3RjnN6RcwTvTmMFWTaZz4Yshz1OZbus18k9KvYiRGLhMujNrvjhEl1MBoCeKtjJsOQbBI6271e6Kz6+g3WdtuM8pBaKzqtCfk4oMh9RtspjaBACsv5R5YIPE2jkVPUHuPSJ6t8NidN9i53nKBU1fTziLVRG2OF6zJrJzS2RuBv+YikprghwySGIKqoBwHiYCQr6WSYsU9dK4Rv8MIa6Rl8XxM2CrfykubUQ98lP5aScGGCF1WY7Qjla+TIQ/oG1S0Q0qI87apg6Va99ELpRlOabmxNCPfZoEu3auUFNbZ67mXzV3SB/clze9z58+9hUn7uTM3Pv+shfu2DT/Kxs7tXdNa+6S1/zt/9zU9dsa+1lid3xs/4HL/+oSc5sz16xtve/Puf4bqf+qNnvO3/+cBZfv5dD/H2T1x81uO31vIHn75ENS3Cp3wZ8Y5PX2ZS1rziF9/H//WexzjxpnfzJw+6c+zbfumDz3if/qSirD/3fW6t5cG1Zy/K13rOHrCXVfzNX/0of/yZde6/1GNS1nzq/D6/+Eef9ecuao0xV4pStbF84twe28OCh9cHz/tvnTJlypQpX5lcdTPYQojXAX8dF8NrrbU/+0I913e+9SMA3PIzf8rPfNvNvOHOo3zgsW2Az+l4nfvfvwWAh9cHh1+0tTb8w/9wHwutiF/5wFl+6NUn+bZbVwg9ybvuX+dHX3sd//Q/PXTF/Z9CG8tvf/zC5xzTj/z7T/G9LztGP3O/0sdFfehE8ZQ47MSb3s2PvOZaTi+3+InfuY+f+J37viivx5QpXwr+/u/cy//yjadZ7+e85X2Pf+7tb/8033DTEt9y6zLDvCLyFbf93J9xy5EWjdz0OAAAIABJREFU73rj1/D2j1/gTb//GT7106/jzn/2XgD+x68+wT/99psPH+OBy32unW+QV27Od5TXfOiJXT70hAv/WW5HrB94c7/5m2/EWssNP/0nfN/Lj/H9Lz/OtQspoad46/vPHMbcw5WfAzcsNrncy/jh3/wUv/tDryANr7qP06sWEWkXHlErMC6wxUiLGfmotutKC2nRYx+rakToutG2luilAs8z6N3wQAgpoZB4aUmd+64THmnsQVqf1rjURgki1kil0WmNMQIaFWjpZretgEIhGxV2L0C0K5RvMFogAmcbJgOXBKk6JXoQYJsaXUuEdnZeunDdz3EZoKQ75sQv6VUxy1GfC1mX0ijubF/AF5pM+9yzs0onyljqDhjXIZ7UPDGYYzEZ8uDOEnPJBJ0IGgez0CMdslM0GOmCx/oLrDb2+cQlJ6TuNsfcNrtG08tZz9uEqubSuMOxdJ+VuI+xkr0yIVYVAxsxrgLm4xH7RUKuPYwVdKIMYwW7ecpMOKFfRfSrCGtd2MyN3U12i5Rj0T57ZcJG3mKDFqMq5OTMHkeTHlIYaqu4lHcAGFYRDb/klqPrZNrn0qTD5qTJ8dl9BlXErd3LtLycD2xeh7GCUiuEsLSDjM1Jk2EectPSBtoKtooG909WaAQFZ7dnWZ4ZUGmFtoK7Vi9yMt2hqXKGOqJXJfQqF14zqCJqI9FGsjZoMb7cdAFBR3s0koJ2kLEhm4jQvXeqSiGFxReGjp9RWSfuXMvaDMqI1bTHcjJACsukCrhv7QjpasmpdJObkjXeuXkbm6MGufZoeC5tssx8bKlYPLrHsIrolzGPjZd4ZftxelHCJ0bXcD6Y47pwk1viSzRUzqdHx3jSn+dYuEvHzzAHnf5Ce0SqIvFKZoIJy4nn0iOriOvSbVpejmcMrSDgsf0FBnHE/iRmJskYZhF56bObpYRhjecZKmXRpWTzXJfmypBmVLA3TGmmLh10NA6RzYy0lTPuxywe3SdSFfsmZuHaXYSwhF7NpPTd/nsJnbkRi8f26EQZUhisFUwqzyVxltIJkWuBzRT6aO6EoLVEJE6wSOBWhIQylIWP38mpJgEISxxVDHsJWhqUsuT9EH+uRjUr/KCmDn3KwnOrV+2KuvSwjRphBNoIbCVRnnHPAaCM01okGhXVmIlCSItQ1q1qCJeCKrzn7gx2VX0jCCES4K3AzdbaQgjxH4UQX3+QKvZFY39c8nd+45OH142Fn3nng/zMOx981vv84b2X+YabFq/Y9q7713nHvWuH19/2/rO87f1nD69/9GlJfife9G7e9cZXccuRNm99/xn+32dYst7o5/zRZzb4o89scHLeiRHWehk3/ZM/Jav0FUX6L//XM8/jL54y5eriX/zJI8962zvuXeMd965x2+predW/+C+H2x+4PODEm959eP2p4hrg1z98jl//8Dl+6ptPc6ST8KO/dQ8Ap5eaAPx/Hz1/xXOsPy34ZpBXBMot5v3Wxy7wWx+7wF3HZ3j7D34V95zfv+J+W8OcX3n/WX71L5y/v/7hc/zoa697Tn/7FJzPbelhc4WIa4SyCA2iUTkPayvQgwB8g3cuolyp8JShyjy8fQ+zkmNj9+PJmKeJjsae87L1DbpUeDseeqlAbgXYxQKhLLpSSM+glHFf1sotUQvPgGfwfE1tBMI3KE+jax/P15gDMRWe2x/PCScRFnvUxZFrcEvNRpKVPnGjIJCah3cXCOdrOn7GhckMe3VKJCtm/TEn2zuUxqOwHmtZi0C58Yy1UZtb59dZn7TolQkXhl2ONnqsZW33d1cRJ5u7GAR3Hz3PpA6YDd1K6rB2CtG9MmE+ciuomQ4Y1iGDMqI06rCANlawNmoReTVpUBJI54GtjWRt1CYNStb22zTighu6W0gsEstO0QDg0rDD3ijhpsUNZsMxoazITMBW3mBr0qQTZRS1x9GGc+HYyFs8srVIO81oh5nzlRaaXpWQ+CWj0sWgj7KQqFMzE2XMxhMiVbNbpHzqieOcOLrDfh6ja0UgNdpIjjX3ua11CSkMhfF5YjzP2qhNL4sIPc1gHJFEJeMsQFeK9MiQovAYjCPC0BWqVeW80tECU0kyHQAQq5IYWIyHZNpHCstm3mQ2HDMXjThXztJpTLg8aeNJzXXJFnfMXORD9Um2Jk0aQeESA6WF0DmynB/O0PBLHu0tcGfzHNeHGygse3XKR0fXcnNymXlvyEXV5fHhPJGs2CkaFMZjVIbEXkW/jFlO+tRGsRAOMVYwrgMuZF26wRhjJUpYeiP3IyMJXNy8r9y5o2uFF5f0tpqE7RyjJEE7J899ANppdpjwOS4UE9+9Hl5UudGYKnLR68D+MGGpM0QIy2QUIpQlL33SsEQKy5m9OWaSjJ2tuUPBskwqpLLondC57yjjHESkRV6IsKu587kHeCxFX5tB7kSHntLYUsJaij45RviG4X6CCgzGCJfIKiz1xHOFfOFGS8ROgFzKqWsJwro0x9hNMejARaVLYTGtiqrwEMpgUaDBjD0Xef8cuaoKbOAVwHlrbXFw/UPAtwBftALbWsvLf+F9lM9zrOLvvf3eK67/7icv8o9/7/7Pe5+PPbl3xfVv/TfPvPx94k3v5me//eYrCvyz2+6D8t995PwV+73rja96Xsc9ZcqXK08vrp8rv/BHj/ADr7rm8PojG8MveJ8/uOcy77xv7Yptnzy/z3X/6x9/zr4v++fP/FH01Pk6ZcqUKVOmwNVXYC8AT/9GHBxsuwIhxA8CPwhw7Nix5/UEQojnXVw/E1+ouH6+fL7u+dN5tiJ9ypQpjucraHyu597n4z/ec4lXXjfLX7/j6F/6sf6qYy2uQ1pJ8I3rXoPzkfZA1xJTKVSrdDZZ15ewF2FCCbXALB+sPijnK2wKhWxWrvOY1khl3ON7hrrrlovNikFYge9rapyNlxdoN5pSKaSymF6AminwPI1e+OwKBwcdcqUMRDUCqIc+qllhaonva8pCHgrGwHkvWxTZOCSf8TjSGrBfxoRxzdGkR6+KCaXPsI6ojWJQRuyWDUrjcb4/Q+BpFpORE9gddBsXkiFPDrqc6myTqhKAJ4ZzXNfcYS1rEamazazFI5sLCAFfe/wJTC2QwnJp3GFQhswnY7Lap+EXHEn75NpjY9xiqTFEYtnOUp7sdblxdotG4Lrv4zrgpSuXyLVHy895uLdIbxJTVB53rFxy4xsH3ev1rE1tJGe3Z6lrxemVTSSW2HMjj5/YOEbo19yytE7qlXT9MZVVPDmeZVI767hOlLEcDyiMYlDGRKpiUgds5w1GZcCR5X12xwkAndbk8LU5me5QWcX5yQKXJ212Jin7/ZTZjuvgN5KccRbSTHP2LnaIZsYUhUsS9JUTMXqeoRx5iJazaxzULmXz1ctPUBiPrj8mUwHbWYP1QcIwCTnZ3GUpHTAoI1pBzqO9RUrjcX2yxWIy5GOPXUNrZoKnDEmjYLTnjv1Io0/qlWxmTR6arND1RlwfbrDrNfhA/xS/ffllfNPSAxwJe6xGe5zN5rk07vDkdpebljeZCSdsZk1qo3hwb4lXLJ1nrANOpjtcyGb40zM3EgQ113T3ODm/S8MveHRngdCrD633lDJIafDSCiEgjKoDUaaiKHyqysP3a8ajiKSToZRhuJdCJbic+VAo5lf32V7r0JwfUWhFXvqEcUV+uUFeSra0YFs0WJ4ZsD+JoZRuRMxzHX1rBWquwFpBXSmsFs4Xe77CvxQhrx2R9yJCI7Da+eebSlFUPiLSmBMVoa+phqHrPitNuZVAs8LWCpXUTjCtLUiL0MLZfpYSkYIX19iD81tHbjQN4QTYppJ4cU2lJVZJZFRj+8Fz/qy72kSOW0DzaddbB9uuwFr7K9bau6y1d83Pz3/JDm7KlClTno0XwmZwypQpU6Z8eXK1dbA/AhwXQoQHYyKvBH75RT6mKVOmTPmCnN+dvNiH8OWBES5VL9AuqbE4SFMrJSotqXoRQgtEVKNriVQGPOvEhrXAjF3niko6MVLl89SapBdVbq76KQ4stawWmNxzAsdK4m0F6FXttsW1s+FqVuhSYQPXpTZaYOSB5Z+WKOGOV/karHBd91qitcRogdUS6RlMplDSMBrE0PPZ6jRYaQ2YjSasTdqsJH2UsDRUwVbR5LHdeY61e1RWMh+NKLTHmQeO0Lil5IndORpRQSfK8ITGWMGwcjPKlVHsTlJaQc5DG0sstEeMioBTi06ov5m1GNcBu+OEpeaQUGkaXoEnNIHUSGG47+JRWs0JYy9AG8n2fpNue0x+IKDby1Pm4hGp5+Zo1yZu/rsd5/gNTShrbpjboukVKGHZzRImRcDpxS16RUwga7YmTWfdVgWuS6kVc+EYiaWyil4Vs5en9LOIVx99Al9oCuNhbEhpFDtZiicNa3stTi9vYaxgKR2wEveprRM3LoUDGirnz3evR2LZGDZphCVRXKKkIa88Ak/TKzwGtQLf0okzAq9mlIf0hwmjZoivnDVjGFWusyosr1w8y07RYDnq80B/hZlwQlF75KXPuY0mwXWalbSPFJbdPMVXmu28gSeMe11CzWA/odHJKEsPFdf0s4iZcEJlFMvxgHt2VgllzVc1zjCvBry2/QjbaYuHJ8ssBgOuCbcoQp+NsMV3nPoM9+8fYSbksLvfiXPu31thb5xw+voNF2Azt+9Erv02SeBmzLvphPObs6RpTla4/8ckDw91DNYKDGCMs8hkK6Reyp31ZOEThhXCM6QzboUn8muqWtGaHxH6NWWt8JRhsNGkebyP1hIhOJz5tkA0m1EWHsrTVPsRIqnxQo3OfWwpEaHrIouJopqt0YWHKCXFsQJPWUxg8KKaPAsIoooy9zG+u58f1pSDEDxLELlZ6ao4KHOtQOwFLv1x4iEbFXWpnC4j85CpWxWyucJ4FlMLbC3QWrpZb2mdlWfw3CcgrqoC21o7EUL8XeD/FkJsA/d/sQWOU6ZMmfJCcPNK68U+hC8PJJjtCNuqoJYu/jjSyEKiKwWhRvR955NrBLVQyKHC+gbrWydKLJwDgZAWkdQI6ZZzAdSuj4kV0Y4iX3ajI2bsI+Kaqh8iaknd1oj90MUyK4W37aOXCxh6lL5xX65GYEqFHHqYRn2YLFnlniv0jYBSOmcI44RxtvRAgi8NMzMjJnFI4Gme2Jpj+fiAhl8wqCJCWYMHS9GAesYlBoaypl/FFLVHemyAxHJydpdhGbI2aNGMCpbTAWf3Z5lNJ/TziPl05Nw75nfpFxFxUCGxBKpmY9zCWMFMkqGNpBXmDKqIrXGDNCjdtqZL7ptUPkpYwqgi9p147vz2DMZIrr92m8uTNoX26GURR1oDOsEEXxiafk5hPHaLFCkM/UnMTQsbPNmb5ZrOLo/vzrPa6VEbSb+ICP2aUzNbZNqnMooz/VmksOSVx0sW1pjxJhTG457eKnntsZgMWS9azDXGXDO/R8vPWY76JKokFDVKuGJHW8nlYobz+zMsNYc0DoR1N85vknol2goe2VvkupVtQq+mdeDdnWmf83YGYwWVVvT3U1RaU/Qj98PLCmJVUZiKyipmwgln+nPsDFLK7QQ1U7CfOwHhjZ0NVuN97tlbZVwFfKx3jNNzW7SbE/LQZ7SVggARGPpnZ9i7qWDTSE53tjjW3Of+/SOEsubGeI1Vf5euGnH/6CgPj5aorOJYuMvdnXMHJ9ERdouU9WGLna0WYaMgCGpOzW2xVTZpegVx6t4Lu1lCqRWXhh3nzNIaM5pEVIWH1YJ6EICFSkAtLPLJGO/6EXWtMLMlQViRDSPAkI1D511vBUXuY4wgCiqGg5TCd69bc36E1yrxlcaTBm0knjIMiwBfadKwZKgi59JSSGha6tKJkxEQxBXlJIBWDblyLiKtEind+BiAriRhUmGMQG4FFLGPaJWUE98JGj1z6GnPwHeJjdLCbIHoBdjAYHInaKQSIJ34We0EmPkS0wuciNoKdD9AjaUbQcOHpn4+H3VXF9ba91hrf8ha+9MvlEXf+/7Bq1+Ih50yZcpXML//6csv9iFMmTJlypSrhKuqg/2l4tr5xhfc511vfNXzFhR+7Ke+npf/wrThPmXKVyL/53fd9mIfwpcJFtEt3IiFAALt/KZ9g5TOws961iUkhhohQEcGqQzWKESsnTBS4Oz1pMXzNZUWmNFBh0la8mMaGWg3YuIbZ913kNInGxVWC+e7O/ap5yrQwnW9GxIVavTEQ4w9TGgQwYHFmj3oXAfGNdwSlyZntXDfpgJM4Tyci8pHa0E3nhB5NetZi8VoiEFQWcnZyRyTOsATGiksvSrm4rDDIIsO0/8SrySrfQSQ+BU7WYPaSGajsfPtBjxp3LZ4Qlb7bIyblLVipTWgl8c0/YKLgza+MrTDnL1eg4UjTi/gK82Tl+ZBWI4t7xEHFTujlOtnt/F9zW1LF+lXEZVReMJw89wGHT9jp2iQWx9PanbylL0s4Wizx62La3SCjGi2ojaKTpKR1T7Dwo21RF5NaTz284TaSiLPWQK+avEsiSy5kHWprKTSinaYO+GhMpxo7NHyMpbCPgrLhaILgMIQyprNosWZwRztOCf1C7La5+6588z5TuCoraQbXDnCtVd+VmyYx86WTvoGU0mEb4jiEl8YLucdJJbHB/MsJgOUNCRRSRFEqLMxg1Oane0WK2mfE/Eu8/GIM/tz1LXiM+srHOvus66bqIGHSQxeq4ClikEeUtYe57wuL5lZoxtMeKC/wtnxHN8+dy9LXp9vmHmA7brF+3ZOE3UqfKHZKpv4SrObJfQGCUFacsvyOp40LEUD7tlbpdSK2XhC4pXMJ2OGZcil7RmEsKSJ63aXvRDVrND5gfe7AaRAX5MhauXOz1I58e5Bd1mIg9EJ60ao8gtNkuv30H0f2hC0CqrKo+4FFFGFrzSBpxlOQsKgRhtJ5Nc0ooKxCChTDYXCTyq0locWeMIzCAEqrvB9zbjnxJEAfrtwYkgLQVCTreRuJUyCUBbPr6l3I4ic4Nl6FlsoolaBriV1042Axc0cYyTFxEf6zhrUzJeoQFNXEqEMKnI++DpUboStWcHouZfNV10H+2rhuoVnLsJbkcfLruk+422LrYi3fM/tvPcnv/bzPvaj/+wbn/W2T/70655x+2tumOdffuetAHz4TV/HX/sLntxTpkyBd//487exfLbRjm+5dfnw8lu+53a+5+7VZ32MH/+663jDHUee93NPmTJlypS/mnxFdrABvuvOo3QbAd//8uP85kfPszHI+dfffTvXHkSXR77iX33XbfyD/3BlSuJv/MDLuX21w29//AJv/v3P8G++96Vkpeahg3TH77j92b9k/8Zdq8w3Q0JPcevRNvdfujLi+aGfez1J4PHOH3sl913s8b/9obMPe3rAzHff5b7k7zw+w589tPmXfyGmTLmK+L0ffgVv/8RFfu9Tl/jV//4u7jw+wy/+8cO8/uYlfuDfffIZ7/O6Gxd4/2PbVNpy80r7cPu7f/xVHO0krPUzvuktfw7Ar//tu7lxucV/fXSL19+8xP6kYrbhRHG/8/GLfPfdq/zyf3mCt33gLD/37Tfz7vvXaUYe33H7Eb79thW+52XH+O/+7Yd454+9kusWGtz0T/6UH371tfzkX7vhhX9x/oogColQ9qB9bUg+EzN5SYYtFNozYAT+UFI3resGe4ZwR1E1K2QpUYOQeqXA1BItJCowVLnnHk9aZ6vnOastU0m0VIhcoWsBVmADgy0UKq5dqMVTZIqi6zpnZidEVQLd1IjAuDCMQYAoBaJVI0YK4xv8AyGmqRQy0JhKIgfeoWWf57kZ4aV0QCBr9suY2XBCrDSSAoIxjw4WyCqfzkGgykyUURtJ4rnQl6zyWe30KLRHJ8oYFQHGCnyp2ZmkJL6zwGuFOcMi5Fhr3wVlWMGD6yvExyrmkgm1lRxNe7SPZ0SqwljJqAxZXtpntenmpHdFykzkQnNuXNhkIRpyadJhMR5yLN6jsoq9MmUza3Jpt8PNy+tIYbmus0MnyNBWsFcmBLJmN08Pj+O6zg69MnZJlFWIwR1/K8g51dgikSUTE7CZNzFW0Dvo4t89d54bWxvM+SN8oRnqiP064Z6dVRK/ZC9LaEc5Shj2JzHXdnc4mvQ43dxkIRhQWcVEu+65wlBZdRi489D2ImnoOrwNvyCvffTARyQ11jhxW6hqMu0Tq4pjjX18qdkdJ+5+Kz3G3YDQrwmDmk+ur1IseLT9jOPtPR4pF8lzz82ee5qxb7GhxmgFwjIYxehCcbmW3NxZZzXaYyXs8dBomU+MruGGZINTwQYn/B2aCxkfH15Lr4r52LkTXL+8xfHmPoMsohUfdPplicLwsrnz3LO3ysVeh34/4fTqBqVWhFGFOljtkMKCFuhCISqBdyA4rnciouWxE/YZgcgl2X6MjGrM0Ee1S8zIx6YlplL4yxOEsLRWhlS1Il9LsanGnymoKif2jf2K/plZzOk+VaXIK4/IPwi7ERYV11QTH4zASyuKUQiVwGtWLpznIAwGaZEjhewa7MSnNAF+O3Pn/X6AnS1ch90KrLIYI11ITWCQvkYIS5V7h6tTh6FC1ukthABbycOQKaslRllM7spkoV3nHvVlmuT4peT/eNpy7pu/+cbDy6+7cZH3PuwK1zfceZQ33Ol8bZ9KkFtqOaXL977sGC+7pvsFx01uO9rmvkt9PvLmr2O5HR9uf+ePvYr3PrTJ//wbn+Rbbl3m3fevH6bJ3Xq0QzcN4A8f5EgnfsbH/Z9edQ2NyGN3VPKv3/PY8/3zp0x5Ufnwm76Of/+x8/zE604dBro8+YvfjBCCu050rxi3+JffeeXoxVu//w4GeX3oRf+r/8PdDPIKre3B/rfylvc+flhst2L3MfeT33CK19zgbPX/xt3OP7+TfNZx4u987UnAfR68+ZtvZHfk8q5Cz52XQghuX+1c8YP36ZenTJkyZcqUp/iKLbCfjbd+/x3PGETzZz/xtfyn+9ZYbIWH2z5fcf1L3/dStLG85oYFLu5Nriiun+J1Ny3y4M++njT0+Lffd+Vt2rhiQUnxOfcD8JXkb778+Ock0E2Z8uXASifmH73+NAC3HGnxwOUBQjzze/0v8o23uNGNmSTAU+4+rcg/vP2771o9XOkBVxj/txTC3TTgB7/2JG+Yhsd8UbGhweyE2NRZ7U1uzdx8s3LdZzFRGA9ne9f3sN2KsmOcdV6iMW2D6PtuDjr3sN0CDlT/cqIwiQYDaj9AdysXlewbRCWdHaBnoHQdOm89wPgWM6ddfPNM6ea5UwGRmw9VWwH1bOXmUFvaXZ+rEBOPygpUVCN3PJjTLrziwGSgm07YHjS43G/jzRjaccZ8MKIwPvPBkO2yyUrYY2m+T2UVoai5d3CUQDr7u7PDWSJVs5QOaB+4dXT8jFIraiPxpOGuhYv0ypjaSmojecnsOi0vY69KuX97mfBiwMmbdxjXIalX4AtDYTxqozAIVtI+Td91QDN8mkHBiXSXTLtgl9ooTjU+G0Wxnre5d+MItyyu01wqSLyK2XBCNxiTyJL7+kfolzGxV7ExbHL97DZtPydUNYMqIq/9wxnybjAhVQVtb8Ijo2XWMzeqZawg9DTXtHaZ80fkxkdbSb+O+djuCbaGDdpxzuV+mziomFQ+Ze1RlB7XpLu0PNfR3ipbXMo7nBvM0o0m9MuIUis2dtokaUHg1QwmEWWt6CYZTT/Ha5cYLWDoY+KKTPvMBSM+uXuM5WRAr4xZbI44v9XlmoVdVhoDstpnUIYspwPWJy32VEIryFlsDTmfzbLbc3VCuC3JYuG6rFqQNnOG4wZl7vNwf4m4W3Eq2qDdmXAun+P+0SomFdweXeB0uM7EhHx6dIwkKViMXR6fPbCLPLMzy0JrhCcMpxsb3D5ziZ20wW4n5fKgRV76zKQZANoKtvdaqE6JPBejCoG36mbhB4nvOvdhRVl62EQTt3OKzCfo5tSVizGvSo9md0xZeuSVRysq0FbgHdMMd1MA0rhgnIXUWpLetI85CJLJS59KK4yRUEp0HbhVg0y5c7WUiESjnogpTub4QY3wDDKyaGkpxs71BGAyDt0qVGgID/Y3Y+fyozxNWfggLFYfBEEZ4VaZRh4mditOjDxaDyt6dxWgBaKQ0KwQIw81X2EDja0lwY6iCNW0g/2XwVMST33uaPqpxSb/4HksA3/rrSuHl9tH2s+6Xxo+87/gSCfm9Tcv8iOvue7zPs9KO3rOxzRlytVAN70yCev3fvirn1O66p/8/a+hHX+2kP6GF1iHIITgp562ujXli4XAphrhO/Gh57uK1CiDF9ZUdYi3LzHSYiKDCjQUAUhQae1GP0YeIjRYK7C1RHgupc12S0QvQM4VaOO8toUEa0CkHFr5iaQGC/GWYHDaiZ5sohHWFS3UAqk0hFDPghh50CmdUHKpcPv5Aj+unGfwTIUfaMpaoruWQitGeYi1cMPcFv0ixljJrD/meLjDWtWhsm3anhPeVVahsNzdOcf7tk5zsrnLzZ0Nzo5mafgFBsGRuMfjw3kW4iHHYlewDOqYI3GPwnj4QqORDOqYC6MZ7lq8SOtbHyeUNQ1VMNIhO2XKxrhFNxozH41oeTm9KuHCyFnVXdfaYdYf8+H+Ivt5zEw4YSXssVG2uDB22qPQr5gLxniR+7+Vxjs4logn9uZoRgW+1HTTCTOBK+o2sqYbWdhPuX51k24wIZCuqLuYd/nwxWs41t0n9ioir+J0exNfaC7mXQZ1yKQO6JcxW8MGReGxU6WEQU1W+hBArSW3H7mMFJbtsslG3uTCYAaASREwKgLy0tnKJWnBqBczMztCa8lgmGCtYHZ2jFQG5VmKVGKMRFtBpgNes/A457JZAqnZGDbptCYMSuebfaK5y0fWTtCeydmaNNkeNmhEBXPJmGYjo7fjCmy97GzfpDIYrYj8mqJV0G5k7IxS7uUo3YUxR4M9vqpxhrPlPO/dvRF4TZvJAAAgAElEQVRm4aboMl1vxKw/5iUL66yN2whh6aYTdkcJs40Ja3ttLm3P0D01ZtYfI0NLrCr2sgQpoDeJaUQFgdKkac5gq4FeqKhqiZcFLhXTCIIDH/i6VoTNgtCv8T0nxO0XifuxKiyeNIRJwaTwKbUbtaprJyY0RlDWHvPtEf0sotKKZpwznoSEfs3+WhuZVhAZKCRYkOnByJZ0vvXF0QoKhQhrgtiNi0zKyI1yyAOBswXpa6y0FCdr/LBGKwuppa4U/pkYfbR0ox+Bwk9LqkEInYooKsl0iGiXDL8aRCWRY4mJLLZUqNkSqQxeaDG+RF/v/LPF8yiwpyLHqxRPSd72t+7ittXO593vrhNd3vGjr/wSHdWUKX95/vZXn7jieuSrKzrQz8bppdYzrgRNmTJlypQpVxvTDvZfAW7/AkX4lBeHuUbINXMJ/+j1p/nut33kxT6cq4Jm5PHGr7/+xT6MKS8mpUCGGs/XlIPQdZwOlnGFAL9VUiU1nq/RnkEPAuTywdJvpPFDjY6dtZ8MXUfbhhpdKtdhjjRhVJJpgVQWqQzlfkQwkzsrMgHK09SFx+TuCYEy1JXCO+iI61rit1yqm/I0RLhlYu36UU+lx4lIE4Q1ee4TJCVSus6W8AzDLKKdZJhIkHoltZEcj3dZKzocD3c4GWyz6u+xUbfZKlv4UuMLzYI/4LaZy8z5QxJZ0vEn3LO/yuVRm7mFEcfSfWa8iRP1VQnnxl3moxG7RUonmJBrN4Lx8tlzVFaRqJJL2QxjHTCpAxKv5Gijhy81DVVQGI+L4w5SWFK/xFjBhaxL6hcoaVwSY9Xknp1VJqXPTXOb3Dq/jsGlcdZW8dD+EnPxiEkdkIYlq80eoyqkFYxYz1oEsmZz0iQJS9KlkkJ7hxZ5oypkc9Sk2xwjhOVo0sMgqI1irWjz+O48/z97bxprW5qX9/3eaU173me+8701dvVI03SbNhBhSCDYSWRbihOZJJaRkCxnQFHAiGBHkeUEOU5iJ5GFLMdWJOdTRIgjwDbYguA0hLGBpqq6a7hdded7pj3vNb1DPrz73i7jHopu19Bd+ycd6Z417PWeu/da+13/9X+eZ3reQaeOJG3Z7y9ZmpSD7oJEWmxQSAKZbslVy2emF3jpzgGdXkXTaPqdiqZRNLXGuSh6cy4KY4UIWKswxsWWhRCrt+tlGi0iASM8t9YjUtnigqDQDVp5Mm15OO0xW+VcvDLlj11+GYXnsJOyqhNOJ1Gs2ctq5vMhyaUVTaKjWNYqim7NZNaJY3AxiOXmw12U9Hx0dJuPd17luewu2djye6vLnNsuF5IJADZI5k2KFAElAsNOyaoxXN87Y5yuubnc5Y4cspct8UFy2Jlzaz4i0ZbpMqffqehmNetuip0lqEH8rFetJhtWMXiojtaQttU0ytO2Cq09aR4FtbZVNFYzKEomsw5SBoQIVKsEaTy9TkVZx88iQC+vWFYpg946PiEynjBLUOMa5zXSeJTyYBw+k7izlJB58tcN8qMl67tdupfnqNTFVjEfhYkARTdWzKt1ghABVynESiF3a+xTa4q0pVylBKDIWmytCZWiXHZR4xpbK3Tq4rWj41G9NlrzrTXEjyl+kpAerAn5xrLwTbKdYG/Z8hbxN//MR/i2p3bf6WG8q/iR7332nR7Cli1btmzZ8paznWBv2fIW8ci9YssX+LMfv/JOD2HLO00Sq1dtr0UVNoZW1BqxsbRDxCjm4CVKeXzqkDKgeg3OyhhIkUWBkt4EU3g8QkfLLZHGaphUsaoG/AvRydo4QgBlPELGSqZJbIxdluFxsIYQEEL8ERIQHiljlTvGRcd1bCz5nJOYbBOUIQICcF5SO02iHCO9wgXJry1u8D3Dz9DZKLVmNpbJuqribjN6XL0GODBzPjq6DcArqz0+PniNm+Ue98o+iXJ8ZHiHW+WIYbImVy1H2RyFp6tq7tQjPjO9gBSBRDoOsgWptKSypfaGu9WQeROFh88MH3JWd7i52OGoiJHue9mSVFqOqx4d0/D+8f3HIslfev1JLo+m5LrlfJ1zuuxwaTjlev8cLR1dE6vTrxzvkiaWAHTShsK0zKuMl6o97CZ0pJM0HHbm7CYrSmc4qbuclQVlYzDakXUbjLH0spqOaXiyf4oUHuvV40CelU14/uyQdZ2Q5u3jyjRAJ49R6W2rqRYpxaBkbzxnr1ix11mxbhNuv7rHvbxieVaAlZhhDCHxCA6yBblqOS57JMrx7Pghv3HnKu1pTttrOam6PNt7yIeK2/R1xadfu0zeaXBesKwTxk+dI0Rg5mN7W7NMkJ0YjmSMZXre5Y88dRM5Drw02eOXmyfJjlo+kN/hmfQeF8yEnz79KJOs4HY54s5iSAiCh+d9+r01qzJl0I297j1T0dEND6se/+/tG/Tyml5aU5iWbqem7mhqq6msjsffW+O9IE1stLcLsZ/dWkW3UzE97VId98ivLmLlX/lo4UesIq/rBD9J6IwWLKsUqQOuVrSZoq016yT2vafKQVZTt5vvxAD02thHnXiMcTi3scqDKIBuJNWhI7ES+jGIRut4LfBeUM9TQivJRiuWZYoyLoZAeQF9i5Qe72W8dmhPAFqryDoN1ayDGDXx+uAEttQk3YbQYWMLKBCpi7aNuYNeG6PdlXt8vr8ZtjOALVveZv7kN13kp9+jsdryS7jibHkPEQQhd6Sfz3BpgMsVtAJKQ1MrZGYRpwkuCYTCQb3xpq0UQUc3ELoW5ppGBMJKQ+qRiYONl61zErcwOEBkDlycsAPYRsU2EeWxVez9N3mLbTRJFhPt2ipBpm6T3gjeyuhz7WKCHCcpvm9ppMGtNU5EdwGpPWGecPHpKaN0zSvnu6TKMjYrJrbDh4tb3G52eLk+BOBQzxjrFVXQFLLhrhtxpxzR0TXTNudKPsEIh0dwtTjn3HY4ruOEziHJZMuVfEIbFEbENpO1TzhrO9xbDwhB8GT/GCkCpTNI4TlpujRec1J2udY9RxaBlU2pnEFLz1E2Y25zGq85qztcLc7pmYq+rnh5sc9J2UEpz6TKIYNrowmZaslUy3ndoXb6cWtAvUwZHa05KJZI4Vm1KevakGhH02gu9Odc7Z7T1xVtUPz6nSdYLTKU9gz7awZZxW6xYpyu6ZsKLRy116xsyknZpWNqbFDcnffxXlJVBldppHHs78652o9tFT6I6Lxy5JEiIAlo6VAi4IJg/4MLtPTUh5rzaYd2kqEGcWJ+lC54MnuI2vF8fr1DX9fxRit1UCoerjcT7/weR8mU73n2RT59epF1naCkJ9WWRZXGdM9lGl1yxoLmTodwcRX9p4PkMJ3zycMlp3WXl1b7nLZdvr33EjtqyZ/c/W1+a3WNm9MdpvOC8WDF4c6Mjmkokpb7pwOU9MzSnMt59Ou24/gezOooMsx0y062QgvPneUQCjifdSAIOnm0JK1rTesUtlGYrqMYlugdH9uFMseySmkbHRMhswatHKvdkkQ5pPS4hQEVqCpDVjRo6THKsagTjIo30Fp5VBEFjX4VPeorF2+O8cRURrvxq889TWmQpwm+2AgdZ3lMaM0coY7iyro0hLUm2ykJnRa7MDilCE6yanJ01mKnGVWdofYqGLbI+xl2v4nHtbHlxDcKknjeR8FlFE8LGXCzBN8KQs++6UvdVuS4ZcvbwN/+sx99/O//4FuvvoMj2bJly5YtW7a81Wwr2Fu2vEVEh9LI933wiL/7H37sS/qavxf4rR//7nd6CFveDYiAUJ7mehV/9aC6Fm8FIgiUcdjdBp1YCAKfyrhu4AhzQygcUnsYNwQvUMMmVi1VQEiPN9HzVvcb7FoTaonIHFJ5ApLgNsltJmA2oi0hAjqxWKuit/Ba4WVc304zSD153kRvYC9wezVUCu8FqtPi1hohQxReOdjJVo9FaD1d8VT+kCpEP+c9PedeG4Vzt9sxD+po41rkDdeyU3wQ5KrlqfyYc9vh09PLJMpytThnagve37tPJltO2y6vrvfYTZasXPq4untSddlJ1zzRPSGVlrnNWVnDpMkpdMu8zait5oOje/ggOK573JzucKE751r/mFRaXpwc0E1quqYmlZbb5YjGayqneXje55PXbzJvcrR09ExN7TRKBO4vepzfHZLvrjkYLLh88Yz9YoH1isoZJlVOv6jItOWD+/cYmpK+rrhVjjitumTG0t2bMVkUCBH46Di2x5jN33badHlpuseySikrE9+bxJP3K6p1QrdfcnRwyiCNaZVGeNog8UHS0Q2SWMlvvOK8Lih0Q6Fb9rMlksBNsYPSDjmI4lglAoVqmLoCSeD93fu8st5n2Clj4qcXVK3m4brHL6r38WznAVezM/Se4+d+6ZsZPHPOdJ3Ttip+NtpoUVnXms71GUXSsjKOu8tB9DEf3GOgS2Y256X5Piub8u2Dz3GoZ1zLTvn2Q83JuMtv37/MsCiZNymZthztzrh7bxw/9yI+hTjIFyzalNfO4vKq1bRdxV6+5FJ3ymvzMbvDJbNVzuTWiMGlGXnWkpoo3K1bjbUKrTx50sYWEOlxm6pxvtNGcWzePD6103GJswpbaUbjOR3TcH/Ro201h8M5J+c9jnZnjPprlmVK1WaE3JHcS2gvxyq6KiyuleAF6e0E+0SFG1j8RkApZMCvNPlOiU8s1klCrRC5JTE2tpV5QZgl0G3RqUWpgO+1hE604Qxrjb9QgYvpr6ZXRwvFxD1uLZP3MtxhjdI+CqWDQa0l3n5lx6tHbCfYW7a8RfzB3JTv3vg2f/rW5B0YzTvLX/zOJ9jppl95wy1btmzZsuUbgO0Ee8uWt5k3b/LzjcOj1MYtWwBMZvGPxFKNQmmLs4akG+3u7MIg91qaSiO1R6cu9ktnHjyxNxqi4MmJWD0Ggot9k3VlCFbGfs7cbiwAo3gpBIFOLM0ywXSaWIl0m2CRtY4V9kELpUIUIBuJHDZUZRLFkEJga41IopjS2S90WoZSQ8+i5Rf6TSFWYC+YCT87+TBPFsdcTU5RBF5vdqm9IZUtS5fRBkVfV2SyRQrPQK+5VEwBeH52xEdHt2mD4mHV5/+7f5Wnd054dblLpiyV0xzmCy4V08c9zSdNj1vLEa/c2+PJCyf4IDnKZygRUHjuVSMerPrcGJ7R07GCeKuMgTJdUzMwFQ/rPneXscp+1Jnz3MUH9HVNVzeUzjCpC2ZNRsc0VI3h6o1jKqsZpWtsiPZ3NydjlAhMH/Z431N3OcgXdFSDEY7ztsOnH1wi0ZbcWDqm4anLJ3R1rIxaLymD4dZqzIsPDh4L7YxxtIBKHUp5kqzl2d3jx5XqlUt4WBUs2wQfBN2kQQnPtMo5nxfYWpPkLWlieWrnhJ10RaYt7Soh6TZReBcElTcsXEbtNftmwazNKEzL5YMp1ktmTc6lzpSXpnucVF3eP7hPX1dc/6a73Ly/GyviMuBvdWCvRegovhNA6yTdrGZeZiyrlMN8wVCvuZKeQx+Oqx7/dPIc39J/nT09Z2TWlD7BqCjgfHB/xOWLZ2jp+eATd+ibis+d72NH8TOppefG7hmFbvj8dId1azihG5M08zVaOJT0uE5JYxVFEp/oHIzntE6xmBb4jT1l/bsj8o+cY44N+skFjVOsG8NqEdMw93orTlyHpjLk/YpVnZCblro2FFnD+apg0F8TiJaAibFU2pMULW0tY2W61KisjeeUlTTj2DOvC4uQnnYa7TabJhZr6vMcsQO6E/eRIlA2CpNY7BCk9CgVqOYp+aBCKU9ZJojM4RuFUDHVlUI8fgJl8pZqnRD2m2ir2Ci8FpB4pFPY/CuHoj1iO8H+BuFTP/rHePnhgj/393/jnR7Kli1btnxpgsBZ9djVQz1M8Jc8yQNDeKLBOUHQUdykHqbYvQZnDWiPnGtkI3DGE7xAGo9fGWQpCXsevzCIRuI7FqyENPpXy8TRlCaKINcaJ6N7gL9T4AqPcIKgAmqlcD0XH1Nn0e+X3TrGZwuolimhjCJJEo99dLfsBCEoMB5zP8E+KcmUZbbMkCLw2fIIU1henBySSksmolCqqyoO0xiVLoXns4uL9E1F6Qy5asllQ66iP/XFYsbSpdxZR9/qJ8enXM4nTNuCVFpKZ+jpCuslS5fyymKP1ycjro/Pef+V+wyTNal0NF7TesWddoj1ksI0dFTDWV1wvO5xrX/OfrEgU3GM98s+ZuO2kmxaQs6bAhskjdO8er6Dc5Kj4ZzLoyldU7O2Ma317ryPUT66eqQNF6+ckUjHok1Z2YRlm/Jg0aNtVUxF7J/Hv1s11F7zu5OLhCBYtQnTdR4dOFKHENAsEmQpoR+oa82N/TO08CzalEldMFnnzOYFBAhO8sALkvuGZuxABlSvpZ6n6LHnt1+9yrc983JMJGwlba2RMtB4zcO6z/s693EIjps+u+mK43WPXLXs5ku6/Zi0eVJ1OV13+NX6Otf6ZxwVMxbjlOPTPia1iCtrRKMITpB140R2ct5lf2/OYX/B/VmfV+e7CBH4xM5rHCUzCtlw1nb4f86f4hOjz/N6ucNJ1aWTNkgRyPsVhWk4XnYZpiW5arnYm/H6fMT5vMPeYMl+saCjGz6ydxcpPJ+bHnB7McR5yWF3QWFaJIHGKBqnuH885OrRGUZ6dnYXlI3BOklzrUJZRTuyGBE4Pu1zsDdjtciwVlE7xXqWo9Lo5lE1hrNVEc9T6bFWM3/QZ3GuUTeWm8jz6NyDjDfawnjaJt5Uu0YSOhZ/mhJyTzqoUP0mnpPG0zSaZFThbLx5DrWKx6k1wUqyfo1tFc5KVG5paoM2liSxlKUm7dW0tSYA9jSDfktwkmqVEKzEFC3tLAURMLcTmgstzZ4Fs51gv+e4OMwJ4b1YG/36453uwv7sX/1eQoD3/ZV//LYc7+f+029/W46zZcuWLVu2vFv4mibYQoj/EVgDS+DDwA+FEB5s1v0w0AdGwM+HEP7vzfKPAH8R+DywD/wXIQQrhMiAvwHcBZ4CfiKE8NLXMr4tW95Jnjvqv9ND+KJkRr1tx/oHP/AJnrvw7vx/2PLOIGT0yhXKo4zHHTSIAPZKBa1CqFhddNMEu9NiMoutNTq1tLXCZ4CT4GIipOi1qJFDiIAfOdpVgsot3spNJaoheIkPIFSAXotvJaJUuKFFGA8C5HlCOKqQgGtUfJQ/N6ADpl+TppbVIkP2WoQMKOVjFTVziI4luFhRd5cdiyaj0ZYsa7Fe0aD5mdMP8237rzK1Bf/o+P2M0zVHWaxel85wOXMMTcmDqscoKZk2OQ9cj8oZMtUySkpenB5ypRtt2FqvuF8NyFVL7TVtkNwthzwseyjhKXTD1dGEYbLGB8n99YBRuua12ZhBVlFbzW6+RIrArdWIWZUxztcY6UiUZNrktE6R6xadVhS6icu84mxVsCpT9gZLjHJ0sxojHZmyrG1C6xWTKu6/WOZ0ihopoJvU3F0MmM6L6Ce+8So+3JlxqTd9XL2/tRrz+ckY6+RGICixa01vd8XiuMuFK2d0TcO8SVEi0E8rMtXy+fmYs2mXJLW0rUIpT7tIML0GbRx14mClkUV8b9ZNFKp2BiWVM5xOu5A69J2U5LmSnq5Z2YQ2xGvmfjLnheUFCtPw6myXfNxyLTslEy3/ZP0+zmcdTGI5mXd5Zv+Y/c6SVZ2wXkaf5lAr2FR0l4uMvFszX2dc6U8Y7JXcX/VxXvL8/IgnuqeM9YqRWdFVA35tcp21TVg2KbXVKOnR2jGtcso64fZ8gEdwrXPGTrrCjwStV/zmncscDhc80T+lo1s+NL7LrdWY3797RKIctdVo5RikFb2kZtlPmVcpIQi6aYMPURgo+zH5UmSO9SSnv7vifN4BQRzHssDkLdrElphylVBk9ePkQ+ei2Lh4dkmiY1tPU5soKBzVuFlCyBzGOGwbq9lp0RI6DSEIbKuR0tOu4pMov9bovXW8XihPqwzeS9KipZqnKOWpy/j6yjjadYKrFL2dFSq31MuUvF9hdfyM0ErEShP6bbTk3Pjhq15Lm0Zxpcw9wb19PtirEMKPAwgh/hLwXwL/iRDiE8B3hhC+TwhhgBeEEL8MzIB/AHx3COGBEOK/B/4j4H8Ffgi4FUL460KID26WbUtfW75ueTd6Pv9nb3NM+TbJcsuWLVu2vBf5mibYjybXGySxkg3wJ4Bf3WzTCiFeBL4DeB7IH1W5gU8B30+cTP9x4Mc2+3xGCPFhIUQ/hDD/Wsb4XqKTbDt+tnx53u4J9pYtf5AQgEYSErClRvUbXKkxRYutNb4WqNxB6sGLmMZmPO0yQRQWvCA0EtOvY2W6jT2YzkqU9hDArQwyt6gsWv3ZSpN0GppFAipEYVPPIucadmpCEPjMkyaW+ixHFDYKKXVALhViEEM4dGJp1wkycVgfq2y+lY8FUsELlPbcX/RYnHcY7S64tR5xo3vK1eKcO9WQoSn54PAeRjhulSNem++wm8fURIBCN9gg6ZmKnoFJU1A5w2en+1zuTfFB8KDsRXFhmTEqYorf7ZMRNw5OUcIzTOOytU14uO6zbBOmq5xFnrLfWeKDYNRZM6tzbp2P6OY13bRmP18wazJuz0dUraaTNvSSitOyS2kNr7x6CE5w4fopALMy44nxGZXTaOm5t+wzW+aPrdKsVRyO54zzNY1TTKucVZXEpMvXctL3zbg+PmcvjZX0O+sht6dD1lVCkliqdYKvFdmgZni4Zq+zJBmdI0Xsg1XSo6XHeslp2eX4rI82jnKVPA4TIsSnJnVp8JWO9m95i1GOpGio1gnaOKyPIrlgPO5KRd1o+rrk988P+UDvHi8sj3iqc8wvv/wk779yn8YpfvXeNfauLXhfdo+P7d3m0/IiZWOY3O9z04y50J8jRSDNYxIhMoCA1TLD1wqfPQqDiULJ6/tnrFzKvfWA3zy7wjODYy6lE27kJ4zMmt+bXyRTLS/OD8mS9nFaaJa0zF4a45+UHGQLxsmKkV7TUxUf7N3lbj3kuO6hpYsWkL1jLj0VxbMvzg5Y1CmLJuVqb8JTOydM6oLKah5MemjtqZYpaSf2P2edhn4RLTaLtGFRZqzvdxlcmrGyMYjGlhqZOhLt0NqjNgmpUnsS7ait2lwLNumpG7s8MTeYQRVFx8cpPntkuwcmsVTzFFnY+DTgVgc3Uki1SWxMHK1TsWJ9bmiKTTVdebyL56g0nsWkQMiAWGia1KC0QyQx6TU5WmFbjZuZeP0R4GpFUrQ0sxSn5RcSZ98EX3FGJoT4J8DBF1n1V97Q9jEE/g3gT2/W7QMvvmHb+WbZCbD4Issf7fPF1v1LE2whxA8CPwhw5co2evkRo07yTg9hy7uct7Oq/sPf88zbdqwtXxtCiO8G/hRwDIQQwn/9B9Z/2RY+IcQ+8Gngvw0h/C9f9mA+fgZVZvGrFDdLorVOJ8BKg/akv5+zfrpGbCLO/Uoj8piwJlTAefHYESRYgbUaJFgn4mPeJD7SdU38IhdrRbvKEQLkKEauU0n8oEVsXkt22uhrPWiim4gOiFZiliLGLC9S8JAca2xH43OP6Fj0cYLLPdIJ/MCCgapM6I9XNFZzlM+wXjFISn7r3mUuDWd8YHgPLwRH2Zxctaxsig2KF6cH7GQr7q/6FKZlL1uihSeRlq6Jrhp3VkMar0iV5emdE5ZtdFT4wMV7ZMpig0QSeFj2ePhPL5F88ow8abm+c44Pgky1+CBY24SXn79IyDzvP7wPwLQpuDMbULeaflGxV6yY1AV3T4eYxHJ4+ZxUOcbZCpsr5KO49zrDSM9inZFsYud3+mu6pqFjalZtyrxJOTnrMRyuUHlg9IkzeklFz0SR4MOyxwuvXQARCC6mcd64cIokxDYV6dDSU1nDadll1RikAK0ck8XG7SLEpE6TRpeaYX8N/TVSBBqrEMM40Uu0I1GOXlbTdBWNVXRNjTaOttKYzD62WTXS4xGMkxUPmz7/5rMvcGs9omwMUgR+d3qJ0e6Ky9k5ctfzmckFloOUImk5WXXoZjVlY5gvc3AC1bW4pQYTkNJTLlNuiyFCBA7SOdfzE54uHvDS+pDPzfa5ZwZ86/gm+2bO013DrXJEr6g4uTdkdDCnkzTMq5TrH7nLICm5tRxxixHfsvM6A73myEwY6RW/3DxNV9U4JCuX0tMVhWyQQ8/CZrx4fsDSRj/1K93JY29zHwR11jBfZXgXzzkhAnWrGRUlizJDDhsGecVs0iEpGtwyw8u4TTnNGHRK2kazO1ow3dyAqV8Z4J6wWGMxN3OasUPs1KznGWGtoONoZimm19DOUkQe27mEhCRxVBcrfCsxiaWcZojEs5plCBWQFyra0sRWDy/x0wQ8uNyh8thOFnZr/HmC2i8Jm/YxKQNJ2lKmsZVHJB4xMfjUoafRO9uXb76Q+RW3DCF8z5dbL4QYAH8b+PMhhPPN4mOg94bN+ptlX2r5l9vni43p7wB/B+BjH/vYVtn3LuAv/4nn+Ks/88I7PYyvCy6Pi3d6CG8L33Rl+E4PYcubQAhRAD8JvD+EUAshfkoI8V0hhH/2hs2+ZAufEEICfw34zbd77Fu2bNnybuVrFTnuAn8T+OEQwl0hxJ8OIfwU8DPAf7XZRgPPAY96sEshxOGmTeSPAj+7ebmfBb4V+OebC/jvbttDvn74gW+7vp1gv0l2t4ErW95dfCvwegih3vz+KWLL3hsn2F+uhe8vAX8X+Atv6mhORG9qLxDDJgoWZ1GgJPrx9/UTDdSKIAOq2xJSHz1pVzo+ZpfQrg1ChU1VK+AbhSlanPbgZBQ5bqrl5NE3mFYSAqhO+9gH15ca0UroN9iTHDlukJkjeMBDve/oJpbQg3aa0VxswQObxDfhIXQdYePH7VeGw2unFKbldNkhVy23ViM8gm+7fJOzusPr6zGzJueZ/jGN1zReoYXj6cExNxe7jLKSRFpuznbwQdBJGnayFfMmYy+PnZiNVyzbNFa4lUULz9KmnJcFLgicl+x91116SXxbfb/fVR4AACAASURBVIiit1vzWH0FuP7cfXLd0nj9uHJ9YTjHBxH9h0UUwfW6JYl2HBRLtHSsbfJ4m5NVl9N7A7p7K5TyXB7GNpauqTmrOvg24+a93ShMKzWd/Zb9YoGWHi08J1WXaZVz9/YOwnikDlw6OqUwDbvZEh9iG8XaGs6qDg/mPcoyIctamlrjNu9zqBTpQw3PLhn11hSmJdft479bZR4XJLXVtF7igkCJQG5aBmlseUiNpbQ5zknSrGVuc4ZZyaQtqL3manbO/3X7QyzLlLoyDAcrzquCXzp9hmf6D0ml5X3Dh/SSmhfuHNHpVEzqBOckbp6QnCnCoCasUorrcxJtGR2UnM47vHJ/n0xZnuvf5+n8AR/v3eRSOuFXzm/wa5NrfHhwF4Cbs12U9HR3V3TThlmZ0TrFTrZiP12wMDWSwO9ML/GCPORjw1scmBnfMXqJTDQ8X17iuOpxbz3gie4JpUsYmxUf33+dlU351K3rfOTiXRqn2C8WNF6zahP6WcXt02EUaFYp3gtap1idFIwvzKJY0XikDIhxTVgZyjrBdBsaq1DasaoTnFX0iprZx1YwTWkqQzhqEZlDaQfK442H+ylBQasMyWjjYT3JCbnFWomrFFm/RsqA6bQoHS3+vBXx3G0FoUwIAULmUBOD2KlxVqITh7cKvVfG1h0nQAWqVYIyHjXR+N02tnw1scWMviNLLc0foqT7tTbt/vzmNf53EZ+nLICfCiH8mhDiF4UQ/w3RReQ/DyFMAYQQ3w/8NSHE64AC/rfNa/0t4G8IIX4ceBL4ga9xbFveBl77iT/+Tg/hXcmf++S1d3oIW7a8Wb5Ue95X3EYI8c3AenPN/5IT7De29anR6F/JoLds2bLl3czXKnL86JdZ9999ieW/wxeZPIcQSqJ935avE/6Hf/fD7/QQ3rVcGGZvyet+5PKQ37k9fUte+1852+atrxfeTHvel9rmPwYeCCF+FPggMBJCrEIIf/+NO7+xrS+9cTEEKwkORKmQoxo/jCmLSWapznKEFbFXuokCRpO3uFsd2I3Ji6FSkESx0SNxITIQvIxVbeljf+U49lPLTcU8NBK/NKh+gzg3+L4FGZClwJPAoMVVKtr/SQiDFqyM1bp1ghlWeC/hfoa+vKK538F2/caKLI4BH/t2WxeDL2ZtTqFbbi52uNo9Zz9bUjtNIh2funcd6yUXBzMy1ZKrlqNixtomZMpyY3DGSdXFB8GdxZAL3Rk+CJY2ZVrl3Hk44mBvRqqirdiyTmisZliU9LMSs7FhW7UJZaupmvikQGvHbndFxzTUVnPrfIT3giu7Ezq6YVrnrKymdYpuUpM/qgYjOKs63J/0kTKQpw3rKmX3woxuWpPrdtPjLbFe8dqdXdJOg28UnVHJweEZPVNTOUPdaNat4XzRoS4Nvb0lvaxmL1/RNTU+COZNTmkNHsH9WZ+m1vi7OfLSmrZVtIuEZFCTJJa1Srn4yYdIETDS4bxk1SY4L6msJlFRyLiqE6oyIc1amkahtedgsHhcKcduUv1CDI8ZJmteXu4jCZTO8N0XPsdLy30ar9lJV6xswmdP97k1G3JpMONSMeVSMeV8p+Du7R3SQUVba0RhaXOLBqQVNI2mrgz93SmHwwWV1UzrnJ9+5cP8e09brqfHPJff5erRKS9Vhzy/OKKjm5hs2RiMcjROYb2krgxrm1AbzRPFCYVsuJTnrF3Cb06vcCGf84HOHZQMfKi4zRPZMa9W+zw/O+J41eXZ8UOGpuRKfs7BU3N+4/wqrVNkumXRpExXOZeGM8b9NblpCUFQO8W90yEijSLG1imkcvjn+3Q+PKEyjmqSkY9LFss8CkmtIs1apvMiJqsaT6gVutsilaeZpRQ7a9YnHdSFaJnplyba8DUauemNTxJLUxbUKon2nYuE1ng6gyraOgbwUkPHohKHdwJ5uYm6jUrR1oqkXxO8QGuH7jvs7Q5uaLFewNgiFho5avAXHcIJ9CA+MVF/CJGj/MqbbNnyxflTH730L/z+g99xg93uVmj5VvKD33HjnR7Clm88fhW4KoR41Lv0R4GfFUKMhRCPTMwftfDxxha+EMIPhRB+IoTwE8BngF/4g5PrLVu2bHkvsvV1+wbj49fH/Prnz7/yhl8jP/Bt1/+lZT/2fe/jx77vfVz70Z/9Inu8t3irQjUF8J3P7PGLnzt5aw6w5T1HCGG9ae/4n4QQJ8DvhRD+mRDirwPnwE/wFVr4hBB/HvgQsCOEeDWE8I++9AEFeIEqLME4fPPIsita7WX3NNXVBqkcMtu4gdgYYS6NxzcK2W0J5wn0Y0Ur+Fh1dK2MwRfG4br2sd2WEPGclHWsKflcIg9qhIuOCH7PE1YapQKu3VTFA+jE4WSgbRUyiX3crtQwbgm1JhiP7LeEtYYAUgVCLWm9ZF0nSOl5ebrHR3bu0jcVv39+RKotT/VP8Ag+uH8P61UMEGlTbi3GHHbmzJqcBYFRFoNfAEjABsUr0yHTRc6F8ZxLBxPK1pBpS2M1+90lrVcY6Vg0Ka6WPHwwJOk0HI3mJNqRaYvchH8cr7rRDUN6LowWpMpyXhXcvjcm79UsROCZvWOO1z2sl0zXOdP7fcww9sTOPjfm8APHj3uqZ3XOvXKA85LGqsduHNeunOC8ZJSuebDq8+BsEPttgU5eY4zloLfkIF8ghadyhgerPnde3ic/WrI+L0AG8kFFOXD4euP0kTqcVawbxVMXj9HSs2xS1q1hXmbUtY6x6rM09v53NvaLgLWStjSobsPrLxxx8LEF81eH0HO4WrG2kmqo6QbJUT4jVy1GOAa6ZGAqjrIZV9IzZi5nVufcnQ347L0D5jsZh505V3oT7EXJ+TyK2qUKuLXGyUDoeIQXtCvDWV7wgb0HdHTD75xc5NJ4yvOLI87aDh/rfp4dveRD+W1ckPz0qx/iid0zXi136GY1k2VBlrSYbsnJukNpDX1dcak4Z1fP8UhGes2desSvzW9wLT9joNdcMBPen9/hUjLh4bDPS8t9FiKQSstRMuMTO6+xdCk3l7vs5Stm65xJlUfnlaTGeomSmk6nomk1zgsa4nlsPjSlKhOU9pidNVrFim+WtCgZKBsT3UicAhWQ2sXqdqswvYamNpvPV4i2gKMqhtRsnhIp7ajKhNCxFL2KcpkiMkfyqCffSYQAYTxZt8Z7gRCSLGupa4Pp17SliX3xpaYYltGNSAG1RA2bqKfYibaZUnpQUcsRpglu0Lzpa+t2gv0NxnNH/bdlgv0j37u1YHun+Nee/uom2P/2hy+8BaP50mw7RL5+CCH8AvALf2DZj7zh31+2hS+E8PeAv/dmjiVagcxsvAndTHxxAlYJrQq0l1uQgbY00XLPeNAhtl8A+sTgDgKqlLDrsJVGrBUhc4gkEGqFVwGVeLwKMDeExKEepLjcE5KACAIhoqCOTWJbyHz8EneCIKKNX+sFQgW8j6mQ1sYJukpd/OJ91DQTiGMEfMdxOuvyxP4p52XBld6Ee2WfC/mcJwan3FkNOa07HK97XOmdI0XAIyiURYjAveWAB5Mel3en/PbtS+RZFOpd6M95bTLioLdkkEVR3iMLOyX940lzbTWTJmf5whj95IKLF84pW01hGlIlKa2hdNGabjrt0O2X7PVWaOG5OxvQOsV4d4FRnt1ixazJuX8yIMksibFcvHZKP63i8XY24w+SyilePxvRHBfQtUjjOdiZMdikQPogOC273Hswiv/fXpFkFq0814bnFLql8Yp50+HubEDTaNS4ji052j+2zTu8dI6RnnG2ZrURW3ZMQ6ZaXj7bY3ZrQHq4xjlBO81gI5TlfoZ3Bp9Eb+x6aUAEmlrTvTrjrOogDmrkwxRQ+IGln1Sc1wXXijNKZ9hP5tQ+CkQL2ZCJhloYlPQk2lKVCbcfjni93eWbnnydC90Zk0VBt19SfXaI6zt80DwySxXGU35uSDU+paMbPnHwOlJ4Vjbln999gvIw4UPdO1xOzrienvCvX/scizbjNRV1DHkaUw6BzQ2N49XlbrwJUCU9VXJgZvRUxWvVDv/43vt4dnRM3THs6gUDtcIIS29Q8dnVIS8v9jH9eBNRyIai3+CQZLrFeokPglmTMy0zxkXJ/LjL6HCOdYoQPP5ugb2yQiqPUp5uVtNYhTQB6yVCOMp1Qr9f0jpFVRl8o6jXBhYGOa5xC4PIHW0jkVk8z6pFTtqtsY2iOc8QXiC6bTz1rCTt1aSJZbXK4uT6dkbYbx+fr7bWuMTSTDLMsEII4o164qhrEwXRgzZa8xFvomVh8SuNMwGZOMTDFHFQ4+s3n4S8bRH5BuPRReitRn6ZA13deW/Y0L1TiK/yTX6r3pc3+l3/5Pd/QZax19u6pWzZsmXLlvcm2wr2lq+KLzfF+z//wif5y//w9/m5zzz4Mlttebt5q+69/sy3XObf+tAFhIge3z/5/R/l9nnJ0we9r7zzlvceHnyrEAuNOVzjZcA7gXcC1WtjyEsTWz3kuI72Zt2a5iyDAP5ChZTg04DRDlslqPEj+y0Ld1LaPUAETLfBdmM4hr9QkaSWepohlEebGDhR3+p+ITTGOHweRZNByljdJsRqrfEEDzpz2FojkyiECwsNuYtpb5MM1W/odyq09GTakquWymleWexyo3fGjd4p1iuWJuVXbj7BaLCikzRIAh3ToIUn3bMo4Xny4JTaaSqruT0ZcjCIRi7WSx7OepSLlMPDKUoEylbjvWS1Thn0SvY/8pBU21gpbAwnm3YQ5yS2VQz7a64enTErM9at4f6kj3OSJw5O8QiU8GSq5f6iR7dX0ctq9osFiXLMm+yxTd+DZY91nVBXhjRr6V2bkGpL/w2V60ldUFvNyazLcLxEK88oK8l1S6Is1kuWbcrdxYDJvKAoapTyGONYzzP29ucY5djLV2gZUzQTZZEiVu7XNuG47rEqE/ILS9bTnKxf43uxypkklnLcIlQgfS2lvVERnCCsdUx+XKfko0kUxw0tpmjw82iBKEVgbjNqr5nZglvliKEpWfuE315d4yiZ0TU1QnTp99ZMzrqYvOXV810uD6c8dXDC6brDYrcFJ2JwyjKJtpQq4I5qXp+NuKcGfGzvNiOz5pniAdeLU15YHPEzDz7Ih0Z3eSp/yK5Z8tpyh07a8PC8T6eo2e8tebjocmkw48neCad1l//j5jdxdTThSjHhMJ2xqxc8lT/kxtUTli7jZrnL8+6IK/mE2mt2zZJr+RlX8nM+v97BZZKFzRibFbWT5KqlRrOfLThWNr5v0nLxyhmNU6zKlE5eI44qqmmGSBzFaEXdahqr6OU1rZM0Vsd0TYjpq9MENWzwVmL2SprzjGQcW0JkEtuLhIhBUTUpeb/CZRbbKISMgU40khAEWsVqdztNUVdKjAjYk5zsaAVpTAWVnRZ7khNSH89nK8GC1B4xS/C5Q8j4hMPXCt1rsbWKLWgBktTS/iG+SLcT7C1fFerLJALudFP+53//o3zz1dfes97Yf+TGzlvyuo8uOF/1zm8Bu90Uul/4/Xs/cPSWHGfLli1btmz5emE7wd7yVfGV2hSUFHzi+vhtGs27jw9ffvelGL59IelbtnxpROEY7S6o+gZrJXZpGB3Oabsqigk7UdzU6VWx8pxYynnG+PKUsk4IQWBbRXJpSZa0hB1BWxrSTkOeNjTPOrQXlCcF7TSjf7ggAE2jaUqD6rZkWaxslusE9mo6nQYlPUp66rUh79a4vCVNLAFYHHfZuzilajVaesqNAGswWOP6gro2NOcZnYMVUnrG+ZoX7h4SnKCfVhzlMxqvubnYYT9f0Nc143TNx669zp3FkG4S48LvL3pc7s+QBJZNyjhf0/pApi3XNlHnZ+sOZWNIjSXfbZgsCnb7K0IQVI3h+v4ZRjluT4e4NC6TMgaqTF7c4dKH7zNZ5xx0F1gvaZ2K4se0ZVTEqvKiTaltwrJJ2eusyJSln5Q0XjNvMl55sMd4sMIHwapK4vsQ4MpoQiLdY5u9W4sRZauZvD5i/8ZZFJZ5yZPjUwAS6Vhbw2vTMWWd0M1rBr01s3mHJG25sXNGOTBvsP+L1fDJOqebRrHZamM92DpFu0qgaNk9mDNbZrhG0h+tUdKjRw4lAuabF0xmHQ52Zzw4G9CsErJeTaEbDndnPDgdkKaW0JXM24xERrHbK/M9PjW/wbAo+a6jzzFpC47rHo3XDEzFMK+YVxndYRkFiIuClx7scWP/jE7SkPQahAgUWcNkkjIarDg97rN3MOP0tEfRq/ncfJ9LnYRdveTITHFdybpIeH52RFfVTGzBXrbktOxweW/CvEo5XnTJjMUHQekSnuvdp6MbHlY9pm3Oz7/yLN/39PNcTCf0ZMWBmZHKlt+cXeOV1R5aeB7WPY6yObtmwfu797ldjVnahGmT87nzPS7250yrnHGyZpys8Qgap8hN+/i8VjKwP55zbjoUWeyd76QNjc1prIq2ibf6JEcrrJfkSUs9qhn21yzLlLbRdA+XaOmjReNZB5XFp0y9S3NW65Smif3rad7SLyrWjSF0aqQILFYZnaJm1ijStGU9yeldnlOVCW1pMEWDMQ7ZrR8HFdWVYdhfUzaGUDSPLSy7RzWtU9SVwWTxyZZ6oorBUuLNq4u2E+xvMMR2GvUNz7/zkYv8lX/4/B96v+94eu8tGM2WLX84tPIM8opBXuG8xA9jMqEUsZ3g0ReskvFRsvOStlNipKef1XHSvfmRItDP6hhnRmyd6Gc169YwuFaiRCAA2aZVQg7D4/1qp+jlFUoE9GZy3TpF97DBBYGRUfTYOMX4WokQgU4SJ3XdtKH1klS5OM4u+LF4LDgbZWs+fvV1pk3Og2WPS8WUnq54KHoclz3I4f66z5XuBC09ibQMkgrZD9gQhYj7xYLTMj4aqqxmZ7BiVucIEajKhGK4pJfWHPUWJNJSpYYXH16EMbROMcgrch09iw+ykkxZhh//PLXVlJVBikBlDfu9ZWxN6TpWbcqiTWldFHJ1k5pM2Tih8ppf/62nOHr6hIu7U5yXKBlbPRqvuD6MgsdZnZPpltuLIUoEhnmFvBb/zmcvPMR6iRaeW4sRu/mKW7MhqbH0s/qxb/flS/dovKLQUbx4VnVIpOX5B0dcGM0YFeUb3v+NH3oQ9PKKbtJwuuxwcWfGrMz4/9l702DZsrQ871nDHnPOMw93qFv31tRdVfQEzdRAdwuEQDbGDJKDkBxIAThsBAYkozDY/gESYUPIYdkKQUiOkI1DwrJ+KIzAICQMZqbphqaHGrq66g5175lz3vNayz9W1unqpqBu3Zqa6nwiKuqenTtzr5N75z4rv/V+77vZ9tdXqAxaGAoTMFh6hEdbDbMyOveUVsJxYXMEgE1znjrY4L2XnqOrC1pBxTt3bvr3RRU8Pd/kqdMNunFJP8pZixfspFMaJ/nE8RaDToYUjqN5m25csjOYIoSXFbXvP8Y4waV9/0Xjvr0TsjpgVkbccAMSVbMVTtkKJgA8vH2bT+a+SX3WRBgnWA8LaqNIUt8w+ORzO9zq99m6MmU3HrMVTamd4quu1BwUXW4sBuwmU7ajCT2V83j3JrXVjJqU3IQ8PdtgkUSshXP6QUY/yBjXKR/cf4rSamxL0DhFbgIq451v1uIFx67NVn9GoAxSONrDEc3SU7wV+M9LEtQoYRk8nLOoQoz16aTpmp+gdyL/heyFa6oyimi7IVDm/LPbS4rzRt7GSrS0557csa4pW5rKKOJNv62bFsS6QXfmZHVwfv8RQC8pcEDYmfsxR+X5484JGisJVEERayLl3W6EcOfje/Iu73WrJse3GL0kePmdVvy55l7P8bsurRL0VqxYsWLFijeC1QT7LcZ/9tX3v9lDWPE6cmWj/fI7vYFc2/z8Gs+KPx8Uy5TAF6qQizKkXqbsAchltchYyek8xVjJJI/Pq0u1lRjnl6lfvGQ7yX3z3cmzw/Pq9fGog7GSWRH5KtSy+m2sb47yNnOC2ihGWQLA0VkX63xF+nTaAuB41j4f0wvjK5e/wwvbpkVEbSVFEzCtY7I6pBOVHBVtjsoOwyijH+V8erLOrIw4zDvcPutymHUojUYv5RWB8v+vrSQNvHzlyZNNDmYdQmVAOBojOZm3aKwka0Jqq0A6plXEqEjoRr6C/cIy/rhMsE5we9plezCjbLx1XycofQXcBNw4G1AbRTcqGMYZm8mMSRVza9LjmdE6W9dOODrr4pxgtz2hNoqtdMpavEBL6+UbRcIzo3WMlefv5zz3VeJY1RzN29zJuv7c5C3aUUWzrJh3Aj/mWNfUVnF73mNSJkyLmKdON9jqzRhlCbVR5ysZvhKvsU7Qiwq2khk73SmtoKL9Ihs7iaNxilGRYBGcZP68BspQLyuyiyrALq8x6wQb/TmfnqwTy5p+mFFZTaJqMhOhpX9eGlS+ObNMqayipSquDk/ohiVVo4mW8g3w1dHjWcs3Zpahb7I1ikg1XOqOuNI7ZSed8pGTPX75zkOcNB1mNmZXj/hA5+N8Zecp3tG9yUa64KxIqYxiI56znsx5/P6bXFk75cOjC4xq7xiVyor7khMe6zzPfjpmXCf84u1H+GS2w6huYRH0dM6F+IyHOod8fLzNr9x5kGnjP0f9IKOjCtaDOdvhlK1wyqhMCZXhNGthnWCcx/73qQPGuX9vF1VIuTwnxgnKRmOcf08j7Vcr5mVEYyW3l581KRwHow7OCcaLBCWtX+FygkUVnK9ovfAap4sU5wSHkw5FE6Cl5fadAc4JZrl3sJqXkZfOVMH5/aZZflZf+FyfzFu45edfCm8nOC3888va/w4v3K/yOji/nu6G1QT7LUaoV6f0rcqHfuSDr6kzx3/8OUmc98L/9Fff8RqMZMWKFStWrHhrsdJgr3jF3O2kathaxaa/lqy3X1tf6Z/6tsf5vg9c433/w6/e82s8vNN9+Z1WrHgRjZFMs5im8c1I80lCEDdMrvdoX5xyOOlgGkmdBVBKWtsLjm8M6O7MuH3mr7dWUlHWGucEUxFjjC8saG04OOvSvzjmznEPWypaw5zrN9fprC04GHcxjUQq6629tA+aSJKKxSQh6RQcTdrowHA47pxbxd0ZdVHKcvu0d94gWZWaKK4Z1SlC+GML4bh9a8jeQxP2ozm/dPth3n/1SQ7zLlI4TsoWwyhjvzNGC681f2TnECksjZMcZR36cc4gyjjKO6RBTagMgzhnK51TGO0r3drQWMkwzamtr8zNy4i9vTPaoW/6qo2iRDMtIqazAVFcc2Tb5Ccpg/tyGifpBTlZE3KWpRxP22x051zsjIhkQ2k/Mz2IgoZ2WNELc+7vnZ5v3++MmdcRkyohqwNGs5RyFBP0SpK45r7hGbGq0UOvcX9+3kNJx82jIUobwrBBS8tme06iaxqnCJThMOtwOOmgteG4blPebtG7PGaU+Sr8zefW2bt0ytk8pdfKWUsyuoHX6BZGI4VjVCScTNrUpfbNqE7QNL7yfWpaWKM4EQ4pLXFcc2xbzLOY0Y0ByfacplGs97w+PTMhO/EUheX3zy7RD3L24zFsw1HeIdINdyZd8jQg0g29MF9WaguOZm3mo5S0l5NNY1q9glvHA7bXJpzMWxR5SNP1evP7WqekquJrBk8wszEfnl6ksYotPWFbT9jWYwLR8Kl4kycPNrm2dUykGrQ07MRTYumvzY+ML5A3ATvphJ14ylAvuJYcYRLBO7s3uFEO+VdPfRFb/Rm77QlX0hPaquSrN5+mtJob+ZBcheQmIJINkWro6IJY1nTDHOskoW64Pe8xm/sVhSIPieKaO1WXXppzcNaFIZyMOnQ7GZM8ZpFFDLoZ6IbpIqYuNe1uzsG46wN/2gW3TvqkacnRSRchIUm9PnpaQFZEJFFFqL214p1K02vnHM98FXq4PmOa+ZWugzsDkm5BXgWURYAODGlcMp60EAJ63QV3Rl20ttw68aYEcVxT1wqlLEfTNtZK5lkETpyH54ynd58nsZpgr3jF7PWTu9pvt5/wJfcN+d03IFlyxb1xcRUKtOINxlpJPo+QgaVpFEI5qkUInYamUVSlxs4DCCzRek5VKQgtRRlgaoXSlrLW5LMIoXxyI9p6P9xeSXMcU4YN4iBG7+UA6MQ7QRSTCDnXsJXTnMWYfoWpJPNFC4SjyELvgV35GGcVGaK4opqHJL0CU2iK5e/hDmLKHWhqhcsVqt2ggwadNlxKz1gP5jx+4RbWSTbiOZFseH7eY15F7HfGPiGwfUZr6RUdqYbpUo4hhONCd8K48PfaUZaw35swryI20xmtTe+X/ULCHkAnLJH4VMi8Cbgz8b7WvVbO+mCGFI5eVGCHI1JdnTuC3Br3WRynPHjtNsMoI5INoyphVPol+M10hhb2fJy1kxxmXSqr0NJy/XhAPYlI1nIGnYzu2ohE10hhSbX3AD+Y+ZW36WmLwcYMqQxb/RmRbliLF/7cNAF3Zl20MszymKoMvCtMpZEbBVHQECrDfnuM3ja0dUU9UMvGWO8Q8unZGs8er1FNI4J2hVSWIGpYZJGP3U4rilmEkA5XSURskKFldtJie29ElQWoQYmUDudgVkQM4pxpk9DSJbVTtHRFb5mQeDE65WN6nxvZwDeP1t7r+7oZ8tDuIYmuWW8vaBpFPosJkmWc90Ij1x1JWDM/ajEPIp6otugFBWlScSE4pa8y3pN8mo+X+/zy2dt5tPM890VHKByB9O9fNyi8VMpqAmFIZcV+eMbmxpRR02JUp/zh2T5r8YJHOndIZUVbFTya3mL94TmTJuGsavFrh1d5x9rzrIVzBsGCVFXUTnFatVmYkHkT8qGjCzwwOKYwmmb5pc45QRTXNI0iSSrKSpNENfMiQilLs5RhFVWAEN6PfDRpsT6YEUc1plEYIynzACEcdaO8l3Wt4dgnr9ZBg9aWvAwxjaQQXu5hZgHheo2xAqUsRRHgQuG98Y1ETjVV7L9sNZlGdQ1lHWCnAWhH01JUN7Cm1wAAIABJREFURYBIauzSQ39xkhL2SppaUU8iEA6Z+ntJ3W1AOaJuyd2y0hOseMVcfgWTsqsrje7rQiu8+7jW14v3XvnCtWFcsWLFihUr/ixWFewVr5i111iq8FbjV37gfa/7Me41Lv214ue/9yt4aHuV1LjiHnDgSl8BK+plWmIl0V3fkKaUJbqpKR/OsUZSjyOQjuoshsCitKWY+2VbVwtk0mBnAe1nNPOrAhJLXStM20CpCKMa00iqSkMjYd1XoGThP0MqtBizbEIzEoQDC1GvpJxFFC5EaEtVacJWhbOCplK4tsEuAlRisInBLDT6IIarOQOdEUlvLzepEhoreaB3xH3dM55f9NDCMiljxmHCvIkIZcNA5GwmM2LVEOuaji5pByWHeYd2VPGJWzu8ff+2t5uTlqwJmVa+wSxWNWWjqaxiWkTMs5iN3px+nBOrmsYqpLBYJ1k0IWdFCyWtt7PrTVjbuk2kGkqj+ePTHc4mLQbdDCEcgzAjNwGNkxzmHY4XbWZZhHOCNK4wjeLBa7cpmoD99ti/t8JSmIDnFz3vT90oikVIZ22BVpZHdg6JdY0WlsoqjjLf7NkUAb3BgsVZAk7Q3SzpJwVr8YJBmJGoGoXFLGuDEt/gujAhozLl04fr/vxpS708N6ZQCO0b5JpGInKF7FfIqMHeTjBbDpUY7uue0RjFyVGXUjhYWuo9P+nxYOeQnsr52GyX3XSCRZDZiK1gzGPtm5xVKdZ5L+heO2cyT/jE9R0u7pzRjQrmSUlVaJxdjlj7cadBzdWrB0yKmNGkxXHZ5rdu3scDjx3QlQW7KiOOnyPrhXxyscNTiy32kxGhbJiXIVkccpi1OZ20KHYCNuI5W8GE+8MjqkBBAl/W+RQ36yF/PNtHCscwXHAxOmUnGLMZTCmjgLe1b3NStzkou0CXS/EZbVUQRT5R1DjJ/ekJpdX82+cfop/ktMOKrA5oGkVxmqC3Z5hGsbACaxRx4i361gczjk66XNw+Y1r462ZRhhRP9zAbFSWhT9WsFKWAKK79SlLHEJxo3FBQlZo4qZDSURQBZhEgjKAsgnN5mFKOqtFUlSIIDMKAMwK0Q4SWchESDjKCgU99zYsAcRLi5hHyao41CjVVhBsNi6lPZDVz79hlt0rSVkldaTrpqoK9AtjqribCbwZXN1//ieeb7Xa+3YvRanX7WLFixYoVK16KVQX7LUw/CTmc3v23rRfY7cXcnhQvv+Nd8CYXWj9vkQLs3QdC/Une5PfVvZqxr/jCRjiSYU5VaZwR2IVGdb1etio1QdiQX2iIo4amVhBYZGzQgaGahVgnEMrCLESulUhpcSZkcclA4CuVUdTQpA1uqc90jaQ6SpF9X4GuiwC9U6C0wRqJcZrojsZey6hHEbpfobWldL4KFtyMcFcXNJXCLgLQFhEbXCXRQYMRChMKyk2DaCSxrNnQM/ZaE+Z1RDso+f2DizyyfshGMudicsZWNOWsbnFc+KbKUZUs7cosiaqZNRGJqtlvjTFLWzyAm7M+gbScZQmduEQJx5SYg7Mu922eEgcNW5snpLo6r3SPi4RAGaZFzOlZm53NMaeLlMe3bhMtkwpPyxbPjobs9SZ0opJB5INSDvMut+ddYt1wMOpgGsXFrTPy2lvaPXrhNt0wp7GKyiomZUJlFbVRHJz2aLV8Ap4KLBf7Y2JVU1nNvI4ojeZk3iIvA3ACFRrGZy0uXDhlM52xn/qKeCAMgTBkNuSsbjGpYrImxDhJIA3XzwZotaxSFwE6Mr6JNWiwoxA59NeCtRIXWtJWQbaISa5MWUwSwlZFS1e0o5ITfJ+ArSVrvQWjWer16zpjLxlzp+jxQFrwXLFG7RRDPefB9iGRavi1Jx5ga2uMaRSdXs7BuIMaWkLdYEuFTBuktBjrrSoXRcil4YhH1+5QD6UP5tnP+NfHX8RXDZ/ivckzBMLyUHSHjiz4R596H7NBhBaWq8MTplXMTmvK/b1T+oHvN3i23CAWXgPflxl9ldGROR1ZcNJ0+P9Or3ISt7mYnJGqEoWjpzKGes51uc6T8y2edeu0tJ879HROYQPWgxmpKnlweEQgDbkJmJVD6loRHiuifYNIS4yVCNEwP2xj133gixCOQBmUdARBQ1Vp4msT5sctCC3kChKDkA5rBVJbTKYx+wVJYMizECUcRalxVoC26E5JfRbDmkEpS11pysMUOjVKOcygIdDWNzTPQ9C+sdk5gboZw5UFYqukCkLisKHMA9gqsVYQtyqKLATtcEai4xqtLLVw5NXd51C8JhNsIcSPAN/vnFt/0bbvAN4BGOAZ59xPL7dfBn4U+BRwGfhB59xcCCGBvwfMgUvAP3XO/c5rMb4Vr4xf/P738f3/4iP86pPH59t+/nu/gv/oH/0m77z4ysJKvtAmYhudu1s1+Bff9aV820//9j0fZ/W9ZcWfV4TwfsACkNpihSMIDFWpEQKsFYSDAiktzTRBdWrMJCDYrqiWbh1oqAdgMo1IG+jWMA6QoYHla8jA+sm3EwjpoFv7P+C1hEbS5BqROprjGNGvqfoSV2iCQYkODIEyftIXWOoLJbG2/g86ILRDhw0N3snEATpqqEuJMwKDQGHpBzmRbJDC8dDaEZ842aIdVVxIfFrgZuQbCKWwNFbxkaM90rD28opJz6cs6upc3nGct4h1w8m8xUZ7QaKX8eFFwoWNEb3IJxQCFCZgnkeczFukUcXZImXYythcnwJwbe2YQPqJ/ayO+dSNTdY3ZsSqPm92BPjD0RoAx9M2nVZBYxRr8QKZuPNkvWnl/Y9vjvtMpwlCOWwjYRZAq2Cz6xPzpHDM64hb4z6BMhTLyUo5jRCZ4tLDB/TCgkGU0VLVMrFTkruAxiqeHG9SGcXxnR4qMQz7c2ZZjLWC7KhFMCgI04okqpHS0k8K6t4cJS1F488VfZ8s2IlLAmm9bKKVeb/k2l9DShtsLSmqgEEn42Y+oK1KbuYDtLCc1B2OqzZPzze53DplLxqzF49577VP86nxOoPegqpRaG05nrfOrxlrBUoCtVw26sbclH0e6B7R0zlPzzf54v6zpLLipO7wi7PH2AnG9FVGIBq+8eLHyUzI07NNQtVw/XTIe/av82jneXaDMbGo+YPFZf6vo3fxQPuI9cBLRvpqwXYwpqNyoo2aSZPy9GKTwmhSXbETT9kPR95tpH3Es9kaNBHPzYcczdqE2vAlW9cBCKRB4s496LvtnObRkkUREmhDsUwJVd0KrQ2LMiROKyZFTNkoFvOYJF3Gxq9lFFmI7NRI5QijmqoMCAKDa9UgvE950MmR0mJvpaj9DGeF/xLdbpDSkUQV+VFKsJ6jtXf70PHSf9wKMAIR+uvP1BJxsYBGYWcBwUaOtYIgaignMbW2COmQ2iK0xRrhZWxAr10wmrTu+l73qtd4hRBfzXlQ7fm2feCHgB9yzv0d4G8KIa4tH/7HwE875/4+8DHgv1pu/zag65z7seW2/00I8eZ3cv055uGdDr/0/a9cD9xLApT87Evj7Xs9nv7xv8TPffeXvlbDe8vx0HaH3/+vP3hX+z6233tVx3qlGuwP/+hf+FMf+9f/+Ze/qrGsWLFixYoVKz6bV1XBFkJsAX8F+Angr7/ooa8D/sC58/rlbwNfL4R4Dvga4PeX238T+Cf4ivY3AL8M4Jw7E0IUwNuAj76aMX4h8/e/+TGSV+g28et/+2uW//oCKz2/Brz3ytpd7xsHip//3q/gG//hb9zTsV6p9ObP8iR//EL/FR9/beVxvuIecQ6Keei9ZQMDRmCtwDUStfSYFsJRVxrRCEwlQfqqNLWkykJ01PhblBG+IqUc4amiSBXUkqxQUElM4HxjWSmRaYMpNFQSUQtcCE2pcamBha+eRzdD7LWG/CSF9QycHwuzgCY0yE7tpQe3I+pNgYob6pOEYCyRD8wxrQalDXMTc92tYxEkqmZhQrQ0XB2eMCkT/nC0j3WCq90TRlVCrHy1eLsz4860Szss6cQljZV84vY2rbREK4uxgnZQsdmZk9fLBiwniJZV61GZMq9CZnlMNo3p9DPacYmSlnZckgYViRZYBJMq4axocf3GOnGv5MLuGZFuqKymqvS5xRpAEjSE2tAOfSWyMMF5+t5J1uLwxhCRNoSxr0SaWtIfLAjXDbH2v5uxkpvjPuOTNkhHZ5BR5gFSOS5dPKEbFbS19/AujSY3AbdmfRwwXiQ4J6jKACm9JaORMF3ElGcJQa8E5ei1C9pRSSgNkW6QOAqpz6vngLd4WyYElkbRSwo6YUlpNWcf3SC4Mkd9pIN5NGN80mZ374xRkXIYdrmUesvZ54s+N+cD8jogVjW38x67yQQpHFf63if8o3d2EctGSSEcrpSIswC7XYB2LLIIoSzzO20ONrsQwyOdO+wGI0JheK5Y51bR5zfy+3lb7w5dXVBbxUnVRgrLs+M1tnozzsoWti0JRENH5nx55yl6Oqd2ik8udvid+j52kwmPpLdRWFJZEQc1nW7BzMQcVl1mTcyHy4v0gpxUVuee2i1d8nBPkJuQg6LDrVmfzdacWNWc5N4hLNQG7Syn85iiiQhT36zsai95mS1iL8kpQ4oiIIwaqkph6pC0XWIrRdj2DYxKWUwtiWJfvXajENMuyLOIdqvAbpakScW8TrBWIM5C2KvJyxCUQ0qHWJ5rB5h5gHEg0gaXaWxX4HKNC32FW8wVesPLS3RgQDqMkbhaED0TUz+QYxcBVjl0YHCAs3d/r3vZCrYQ4peEEH/4Ev/9B3hJx999iadtArMX/TxdblsH8hdNvF/Y/mc956XG9F1CiA8JIT50fHz8UrusAOLAn97f+uH33/VzXsoX+V4mYJ/L93/w2svv9KeweZeyizeTS2spP/IND7+i57x9796r2MGb3GAo5UqksmLFihUrVvxpvGwF2zn3dS+1XQjxbqAGvhsvEUmEED8M/CvgCLj6ot27eM31yXI/sZxkd5f7svx/53Oec8RL4Jz7GeBnAN797nevSq0vw24/4Se++VGEgG9/z0Uu//C/ednnvFhL/D9++xfd87Ef3+/zf/zuDb74vlfumfyPv+Nd/PPfu8Hf++ZH+fKf+Pf3PIY3grfv9V5XV41HPicx8ae+9XH+2v/6e6/b8V6Kb3hsh69+YINLa3evQVux4nMRAqJWRZWF2EWASI0PmnH+MSkdxTTyeup2Q/JMRPOIDyMJeqUPgFhWSl3imx/VEy2KCxUyMlgBlBK1bGi0BzFys4QTH0wjhxVSGZoiwDkQhUIOS0yuKVODWlZt+aMuwSMLjJGEZxKxZWmOEsSwpF6vCVuVb6A8TCmvFmgj0IGhLjW38gGTOuYo67DdmiKFQwtf+tpKp9ycD4hUw2mZ8pEnLqPbNeuDGYG09NOcoglwgBSOjcGMqtEkQY2SlqN5m0AbTk46qMDSzAKSNd80KoVDaUsQNLR6OVHQoKQ9r9hOypiqUUxnqW881Jbu+oJOXJLomkUdcuusT/NMG33/nCSqiIKGQBmcUZSN5vigh9kUnJ10aPUKqlITDgqaWpHGFUo6FkVILykoGs1ZliwDhAIfDjIoGHb9+bx8aYTEoaUh1ZWvxjrB4bzN2UmHziAjW8RYI+h0c4rn26SXJlgn6LQKyloz2J2QhjXBuiGU5vw6W9QhszKibrxWuDY+JbI2irLU1NOIqF8QBP45Eoe+OiP61S6zL8vBCZJeQVFrTiZt3rN2nY9Ndnmke4dekJPomsudMz5+uk0nKnl+3uP4rMsj+3do65KLwxG3xn1C3fiVACfQe5kPRWkkcVz71RwBnx6vcRB0edfaDWZBwpr2wUQXkxGJqjksu3x0vEdjJTcOhzy8f0CoGyZ5zLSI+H11iaLrGxEvh8c8HD8PwH54RuX8NO/JbJuuLshsyE44JlqmPqaJb2bMTMSoSRk3KbezHtc6RygsFkVLl0TSByj97vFldtsT1pM5J3mbfpzzyee32RjOyKqAbBFjFprO5pxFHhJGNbPDNkG3IopqrJXnWubFLEYElqZS6NBgjESH/nwobbBrfmym8Xr4IPZhVJ1u7vX5scU0kqZSiNj4Va+owUqHAIJuibmdYrWDwNt3ilKi+wXttGS2B/lJSjTM/XMzhUh8Q6p9ZI7JAkTSkHZK8hsd8l6NUHc/5bxniYhz7kPAh+C8cfFvOOd+YvlzDnzviybSXwr8Q+dcLYT4VeA9wO8BXw68MNv7N8D7gP9dCDEEYuDj9zq+FZ+t0/0rX3zxZfe/9qJQmB/9xkcYpCHGuVcULPO5fOu793n35QFXNtqvSBLxC3/rK3lkt8tffPv2PR/7jWSYvr6Sie9635XP+nnzzbBgdPCt777wxh93xVsKZwVSOmRgMY3wHsXGNxMaIzEGkI4o8X64+aWKWPvHEA6RNtR5QNyuaOYBRjrcgxnkGqEcQavCJRIhLXFaM28kSjqa1CAqiRAOUys/gQectphFQGstI5tHaG0I1nJyFSMqL7Gr1izaCJL9GfksRoQ+Qr0oAngoQwHWKBC++fGw6HClfUInKElUTV9n3Cl7nBQtGi2plo2Cm/GcRx+8Saqrc7eP00VK8UQfdf+culYMuhmNkdRKktc+8U5Jy87WGAGYgSCQltpKYt1QNH6ifXjaIwlrTqctykV47qzR6y5otwo223MAjhctGis5yVImU5+yF75jThpUxKrhj2/uEicVQkBZBIRtLwHY3RlhrKQOarbac2qrfFz63P+9mOQx80WMDgxR0FAWAXuXT9hMZ/RCn0AYScNpmXKw6NKNCj59vEYrKWmMIu2+yMnKQWMkDz12g3bgZSShbJb+3g4pLNMqYVZHHM3a3pt5HiIyjez7hjp7EOPWK/8lKAtQ7ZpyEVKWCrZgGGcM2hmTDzhcFsJJhNtrmC1iHtg+5rDs8oH1J3gy22Y7mvD+/U/wm/MHaG1WnFQtRiKlu33sUzRnXfY6E66snVIZxe1pF9mulwmRvulWCAcIru4c8+zxkIt7I8Z1ikHykewSEkcsa3ajCceiw7SO0cIgtx2NleSVvxZ6ScGoTPnnT76LveGEL11/loeT27RkSV9lxKImlX6iOjEJfzTZo2lJzuoWtVXsxBM2wylbwYSHk+epnebX3QPcKXo8v+jRCwsKo+mGBVdbx+y2J8SqBgWLOkILw1rfN5JqaTGzgHRjQaAMpQioKk26ntFJSg4Pe+zujMgr/2VruDdm9NwA161pKkU1D1FJQ56Fy0bIhrrW6LAhDmvmi5huq0BJy3iegHDYZZKps/4eUswigqQmimtC3TBKYoK0pp6HhGFDs156D30nSNKSefMZKRSdxu8jLXXu3Wh846VGbWe4IiCImru+171qFxEhxFXge/CV6R8B/oFz7pYQ4ieBfyCEMMA/cc49vXzK9wD/jRDia4GLwA8st/+fwDuEEP/tcvtfc84ZVrxh/LPv/OLzf6eh5u/8xYde9WsKIbiy4Sfub9/rkYaKrHr50/rIbvdl93mBb3/3BW6OMn7rmdN7Huer5Zvesfe6vr77PNDEX9tapXKuWLFixYoVd8OrnmA75z7F0jHkc7b/LPCzL7H/c8B3vsR2y2ccRVa8Cj748Ca/8smXVNf8mfxZjXBvJJdeQcX8Qz/yQdaXyZJ3I315PXhsv8e7Lr0y+8JXi3gTjPq+9/33rqNfseIc4ZuRTKYRocFZ33ik05ziNEHNFHKnoJhHvjGsUBTKEbUqXjCoVJFBSotqNZhCQWig9n7WIvWNhqZRvrolvD0a0uG0QypLM43RXZ80J5TDausb0WqJSEBKi4gM4jREbJbYTk2de/swJgEMKvIsJE4qrJWUByl0a6JnEszDCzbiOTcWQ47zFl+19SkGwYL1YE4vyDkp21SN5g+evsz7H3mCWNVIHBLHfntMO0yo3zMnqwN6UcGN0YCd3pRJEdNP8vO3sWz8n28pHJFuUFZSNJrGKIpa0+suKGtNt1XQGU58c58TbCQLGie9VMJoylqTFSGdtOT+7WM6YYEUjsr413ejEBP6pfkLGyMSXZ97bAMUTUBlFZFqOJh2KIsAu9DkKoZG0r8wIlCGC/0xG9EcLQ2NVZRLL+yzosXprMXtgwFptyBQlsksZb0/52J3RLhpzq3homUzaG4CJI5AWSyCRRMyqWLvqf2pHqbXgHbotZw6C1GRQe0sZQVWIrQlDBuMspDWzMcJ7a2SJ482vQ0koHcyqkKTtku0sAzDBaks2Y4mPBDf4VpwQqtb8s+OvpzHOs9zO+yTm4Djss1h0yZU3iYuVjV1WyGA6Z0O8XqODgytqOJ03Ka1XvKXr32M7WjCo/EtKqf4f88e5LTwUrwHe4e0dMlOMmFWxxSqYVLGrLUynrm5SXe35Er3hEcHt8lNwMcmu3xsssu1zmds+nb1iIvBKVMVM9xYMLMxHxvv8tjgeT58doG1eMED7SM6qqAlSx5r32JuYvaSMQrLjXzIMFwwbRJ6QcGdvMuiDlmLFxxlHWZ5RCuuyMsQUQmaRjFZNqR22zmjgy5609LqFRyc9Bj2F3S3ZyjpkJXAKYedBwT9AmsUtpY0jfT3iUZS5wEm9omsL1TuTaNI1zOywxai3aAigxAOsbTZ88+XIEBpi23VxEFDJvxrVo1CKUsQNWhtqM5iRCXJC4XqVv51lhVyayUm06TDjKa5e+OIVRTbW5D/+T955101Nv7ktz7+WT/Lz5NUmO/7wN1P5NY/D2Lb/9Mvu3zPz32hEfXznW94dAe1amxcsWLFihUr7opVkuNbkDhQ7PaTP/Xx//5bHuNDz53xLe/a5+d+/waP7/f56192mVC//pO97//gNf7eLzwBwN/4ivv4p7/x7D2/1re8a/+1GtY98ze/4j6++Z33Po4f/6ZH+cF/+Ucvu9/XPvLmadH/+L/7WtrR6lax4rVBCCiKgKBTYpbVIN0vfMNh0mCTxqem5RoRG4J+SVMrmmXFKUpqikmETktqZTBlgAWfCGehyTRulGB6zbndl1IWmTqaSeiT4JSjyTRRt0Qpiz2MadoVUafEGIG1iiBqsFu+iSqMvX7WGIlcL4niylt7KctsERHvLMhnEeaROUJAKBvubx8zWAa2HFVdNsMp98fH7EUj1qM5vzB7G79x/Qpv27nD06MNpLTcPzgl1RWV1VgnMFZyZe0UiaMOFC1dcZi1KaqA+SImjGqySULSLTDGN3ttb0xQ0nKxO6KxkspqtLCMbUKiaxonmZYxN6+vI9OGa7tHDJepjY2TjMsEKRxneUrVKN7+2HX6YUYgfLUYYNGEVEYRKsO4TLh+fQPdqlnrz1lMvG2eUo537d0kkg2J8smCiyZiUicc523GeUxehjS18nrZfsZmZ85avOCdG7dIZPUZaz2nzqvekzrm5qyPWqYD1kYxLaJzLa7dLInTmjIPvNY+MOd2eQC2EQjlqMqA9cGM03EbFRkaJynmIUnHBw05B61OQaQNeplcmNkIiSMUhtIp+jLn2zd+j5ao+EN1kQ9NLrMRzZED39R6O+tRGkVjFO24hB2oak1dauJBg1SWw6zDo73bXApPuKRHzFzAhXTEhXTESdnmoPByyV5QoKXhzrSLVpY0qEE4FlVIoiraqiSVFf3lKslZ1eJmPqAyl3moc8jF6NRr10VDX2V8/fbHSGXFYDOjdJpfP7rKfBixHsxZ1zNSWSEDH3D0UPsAiWNiEsZ5Qt4ES212wMmsRTGP2Oz60B/X8s2KLFcLoqBBtWsWi5iN4ZQoqBHCkWURSb/GblQ+aIqAVlJhnGBWpZSLkDCtSRKvm5+NUvrDBbOnBoT3zVDLlYZo3QfFOCuppyFIEHFNVQQ4J2hvzX2QTADGCqLlZ0ZKx3yckna9pjvol5hGEoSG+igh3MpwTlCcJgT9Alru/DN2t6z+an4B8m3vvsC3LZvV/uX3fNkbeuzvet/9fNM79ihry/Pj/FVNsL/zy+/7rJ+/470X+dnfufFqh/iG8uB25+V3Alpv0gT3uZ/4hjfluCtWrFixYsWfZ1YT7BVvOJsdHzd8e5y/zJ5/Oj/3Xe/9E42QP/ZNj5KGmp/59U+/qvG9kdyrF/ZrreZ56se+nk/cmfJN/8tvvrYvvGLFS2BPIoKdDFPjK8V2eUHPA8KNDCGg1pYg9l394gXdtpEUswiVGG89ZyXBoKQpNTKwOAs208gLC1yjlrZfDSzDPgh9dLpMfHXbWoExErFZ4hyUi5DOIKOqfJUxaVVYK2gaeR7x/kLQhJA+LKTTzSnKgCCpUcrrOwNhOatbnJYt7k+PaauSj0wu8mD7kFSVDHTGX3rg4zRWkaiK3WRK7STX50O0tNwY97k8GHFz3GerM0MKx3oy52DRpaw102nCOy7f9Frpdc3teZeL3RGFCWgHPqAmVjVzG7GoQ0JpuH59g0uXjplWEeN5ynse+TRaWNYj7yZyVrU4ztvcHvVIoopFHrHRm3OlfQJAYxUnVYuiCbg+9j0nvaTgzqiLPtWs75/RiwoefuiQRHkLuGGwIDcBpQ1YNBEfP/MrccdnHX8+K8Xm5oTt1oytZMpGOEcJi3HeVvC46nh7wTpmXkfMq4hxlvBCkkZVBsSJ14NXjaQcxah2Qxg0tJOSaBlyk1UBSVifu6z0ogItLd2goB/nDKOMeePdJ4yRaG1oGkU/8Xr0wgQ8OdmicQotDIFs+ES+x9X4gDU1Z0vN+cvtj/Fl6dP8bnaVJ9U2FsFx0aYbFUgcNyZ9OnHJaa1xRnBn1KXOAw6bHjf6Q3aCMWc6piMr7ouOyWzEUdlhUibcnna5NBgxryI223PmdchZliC1o2wUzy3WWIsW1FZxrXXEfekJgTAUNuB22WPaJPw/07eT6or1aM5e9BmbvvXAx498y96HOaq7TJqEj073uJSeUTtFIMx5qFBbebu+jWROS1V8/GybfBahI+Pfp3mIjHxlOYxqqkozy2NwgmF/jltWtZU0NLOAqq182IwVBL0S6wR1rUkMwrgVAAAgAElEQVS7Bdk0ppqHtNMC6wRBUiOlRV7wq0WUCtmqUdrSSkvmi5h0PaN6posceJeWcNk7EIc11vnPfpGFpL0c5wQq9KsbdaO83ae2NLVC9H1/htYGtZ4BUFeS6iBFDKq7vs+tJtgr3jReSdz3Bx7a5N894Rs3f/vvvp+d3p8ugXkj+aKLrz6E5/Xmcz20X4pQSx7f7/FDX/sAP/nLT70Bo1rxhYoQDmEFZRbgCkW5CEA4krUcPSyo8gBXKXSrxhrpPZSPU+jU6MAgQ4M1gsUkRkeGehYikwYzC1DdCrSjqbR/bStwpX8tbiaI7dI3OWYhlcDbdB23UO0a0ygGa3PmWeQTHgtFLiAIvS1gXSiitRxnpLfq0xYdGBojMUuv5bL4zPKxcYJxkfDUYpNvXv8w++EZf5ztM2pSGqs4KttcbR0TSEMkG0qreVvvDrkNCWVDOyjpb2YcZl26Uc5x3ma37T2gbf+MTlBilk103WFOYxVaWiSO06LFKS1O5i3WWhmVVbzt2i3aQUlLVdR9yTDMqKymcYpxlfDk2QahNrxn/zqJqrFOkqiK3AScli1mVczxokU78sv4kTZM8pjH956nd9lb6m2EMwJpzifIuQl4vuhzWrSYVyFZFVDkIVd2TugEfpK7Gc1paS9vqJ2isAFHZYdRmfLx53fYGk6ZFRF5ERAurRWbxntuR0FD1Wims4SN4Yyr+zfP38vCeJnNoo7oRoW3lgN6IcSqOU/ZvNI5ZRgs+MWbD5PENY2RlGVAklQkuqayinkV8WD/kNwEQMCobvGx6S5PhFvcl57yvvYTPBpO6cgK0k+xoaf8zvx+9ltjSqMZVwnduGSUJfRaOUHQsNudUlufKqmF5dlyg7OmzX54ikESyZr702M6uqATFjxztk6gDaMswVhJoHyjrzGSszzlNPfmAFJYLiYjIl3TUQVXEi/PuRCfcafqYZ3gTtXjk+NtdlsTOrpgLxrTVgV74Yi5iVmYiIWJmNYx4yqhsRItLZdbZ9ROMq9979PF7ojTcZtmEWCsJGp5C8emVl62YQTVk13k5eyzkjS1sqTrGXkZnv8OUlkWWUQrLSnKAIxARobxpIUzgrjlPdaVchA3iNR/Zk0jMc570GtlqfZzpHTYRUC1bKLOrJci7axPmC59rJOwJr/ewVxovKQFfIrjUYzYKNFLa9DqVgu1nXs5VuSTKO+WPx8dVivekvSS4K73/VvLxse373X/zMn1V15bf9XjulvevtflGx/bfcOO92JeSQH7bh1OhBD8FyunkBUrVqxYseJVs6pgr3jTuFv9Mdy9w8lXXtvg3//gV/H+n/q1ex3WXfO3v+7V+4TfK1c321zdbPOpo/mbNoYVK+4VuVnQ7WSUtbfyqiqNlI4kqai0RnVKijzEOQiDBrntmweVtDigqjTOCbQ2mErR7hTkgaGVVNSxYjGJkamXgZhI0kpKqmv1ubTALh/T0qLaNc4KoqQiDWtCbTg+6+AChw4MYdhgjSTsFYS6QUpHUyvMQYK+OKNpFIPegkUR4oA4rs+DT9phSWU1sai5Fh1wf3jE2KYc1D3OojZPLLboBznWSZ6ebvBFw1t0ZEEeehs6i+Ba9xiARNX0gpwbiwGjMsU6yaSKCaUh0g3TMkZJy83jAa205G0bB1zunNHRvrps3bIJEIG0ilkdszAhz4zW6cYFj23cYRgsaOuSzISUVhPJhv/7o4/T6uf005yrwxOsE3zJxnMEwssCUumXzEunmTQJWDirUgoT8AfPXqTXy9DKUtaanc6Ma3vHtHRJIAy18xX/xkrmLuLp2Sbj0hdQFlXomybLkEGas95enDd+Xusdo5epjdZJ+kFGW5UoYclMyNxE3Mr6NE4xr0OMlSRBTaQajJMsasekjNHSstueeNmHsoTaMJ6nmExTa4OSlqKK6IYlSjh2ogmfztY5LLvcmXW5ZXvYdcm8iYgHH2JDedljX2U8kt7muWKdG/mQdlCipfVNp0ahhDvf1gty3tW5zuXgmH83extZscNvn9zHu9dukMqKRNVcSs/oBQWnZYvKKu5Mu9TLYKMoaNhuTZcrGIZplfAbsyG7rQktXTEMF/RUTk9nXIwMkfSrEyeJzzX49HydPzi5wNuHd9iNJgTCsBVOsQg6umAYLs7P9UnV5ndvXGZ3OOGpO5s8sntAp53jWgWTPMY5QRj6Cm8S+RUofW1GOyk5POizu3uGEI6zUYteL0NJx3ianofCVI2mHZcsFjHpICfUvom1aSTDdkZea9pJSV4FDFsZp/OUplHMJwmD4ZzGKJLUv69qe+Y/j0HDLItJW6Wv+gvnUxvjivTyFGMkQeDPNUC1Z2hqf1120oL6Sk1tlA/S6fhm57u+z73SG+OKFa83LzXxfmC7zZfcN+THv+nRl33+C8E2rzfb3fgNOc5LIYTgV37gq/i3/+X7XvPXfiG586/eRfrnihUrVqxYseJPsqpgr/i84227f7LxL9KKn/vuL30TRvPSfPM79l5RBf714trWy4/h/o3WK3rNX/i+r6So7edN8NCKtx5S+YajUDeUta9eN41EBA6lfMCDDhrfWAiES0suKS2NUTgnqPOA1rAkq6XXsWpfgXIOqKUPr7CCVlL6hiZpsUurNrEMn6mWFdQorlHKklUB7ahCSodKfLVKS0sQNihpqY1CSkc9DZHrJcZIoqjGOnwMtvHHkcKxn465kQ1IVM3T5TbXogOGak4sajbUFIPknelzLGzEzMY8mB5woxwybWJuL3o82Dvko2d7vGvtBp+cbvNw94A7RY87iy5b6ZytZMrl9imLxuthd5IJAG/r30EKRyAMpfV/4r29ndfSzqqYUZGw3Z7RDQr+wt4TRNJrko2TZCbksOycR4//h4//IamsiGSDEv49li9Klq2dYtrE5Dbkw8f7GCvZ+v/Ze9NYy7LzPO9Za+21xzPfsapujT2xSTbZJFskLYqSIct2HMqSIcSGISR24sgCYueHFGdwrASBAUlRgjiIEiAIZCiw/cMwBBgOkyiBBgZWZA6SLIrsDoceqoea605n3PMa8mOfut2kSKlbbLKb5HmAAk7te87Z+8xrv9/3vW9vyaqJcI1isUz53mvXGemSQVB9xRCjcZL79YBFG/PMsxfZO5iym60wTjKJc0JlSVRLphpGuuBcOCMWLVoY3Gv0wcYH1E5ztxly1PSZtzHXT7dp2gBrJMN+yc3DCVlWsTjscf7SCUWjyaKGO6shiyZmO805zHvrUCK6UKE10yrhZTnh0YFhP15wrxqgpENJmDUJn71zQOsVV+ITpHD0ZRfYciGa0nrFs8s9Tsr0rLVvsUwY75fczEdMwoIn41fYkjVH6U1+7fRdbMU511fbxMpQ2YBxWBJIyyAsOa56mHUPtk4sadgyDktGukALS6oa7tVDbhUjKhvwxekeVRvw5w++TO0CdsMlQ1Xw/sENpHCs0k4oulmNuVFOOKp7XEqn5DakH1QYr4ikQQpPphq+7/KL3WXdcC/vo6QnCrpq0GKZEEedDZ/1ohtAjBuMlYy2VhzPe/TSikp1vy12Pdys5Hr4WDrKRpOt49C9FyRhS+666pD3glC3rMruPR+HLbUAZyV1q+knFYuiezyxNuRViJESrQ0CsE7S75VMT3usygghPOU8JhuXRGulWwh/Fo8eBl1YkPfQGoUOzaux6q+DzQJ7w1vKb/5HP8AP/fdvfjvHkxdHfO7mjJd/4WPflITH17Owfbvw199gEE4aBqSbtfWGbxLOSoTwzKYZab+mWMTIwOFWGrtQyCs5zTIkGnSe1G0boZTr2kVCS1WGuNMQMW5oTECQteQnXdWl0g4RdAmP3kF7J8NeMeRFhJSOdh4hagkDg7udIC+U2JWmimXnZqItpybAtrLzy05aZqc9vAcVOmytUJElHNWd+0AT0JQaHRusUShtaY2iWS9s8zZkoCukcHy2uMKe7hbBF/SUvixJZU0qa0Y+Z6kSHonucc8MeTy7y0gVXEuOuF2PedfwLr958zE+dvkLvLt/h5WNGAYl1kvQS1qvzhwfCheSmwiD4k45oLIaKTyTKKcfWN7Rv48S7qy1I5UNlQ+4Vw+5WY75wv19Hts5ZBCW7CULHknud6+blxybHq1TnLTdSfu8TVg0MT1d09iAUFnOD0+ZhAU2Ffy5/S+dLdxTVVPYiBvlhNvFECk8t+ZDLo1mlEbz2MN3OCkyDtIZl+MTxkHOSOVn7xuFP1tYV06TuwAlHBJH4UJerrZ5brELwKqJ6Mc1d2Yply8cdw4YUc3tkyGXrxwxL2PaNqBRlp2sc98YhBXzVUJbaqS2rO73cMM5cWA4XmXsbS1ROO7XAy4mU3ajJbeKEVJ4rmyd8uJqmy/MzhEIx5OTWzgv2A0XjIOCx/r3+XR5leNF1vmkRwbjJc/d2iO90lB5DdS8I7yLHQtuNNtcL3b45EvXiOKWQVIRB90i996ij1YWJT3zZUJrFeVAE8kQVMNQlez2Fjyc3sd5yXIYU7uAF4ttplXKTrJan+yUa1eQFi0sj6X3mduEkS64vtrp0jGrmHTtWz0MK8ZRgaTzS0+Dhv3M8fkvX6K/t+L8YIFbaUzS0NYBxiiG/YLZIu0+T+tF9jKPEdJhnWQxTZG6u1w2inYRkUzKbuhReqppTLpVUOUhh01AGHWDqk0dMC9jnBdUZfdjVeYhWlnKOz3oG0yvplxGlMrTH5SsljG9uKZuNQjWg5gSpKdYRngP1UlCsFCYfue/P7076NIiFzHY9clA+vqHHDcL7A1vKQ/vfnPaOf7F3/res37L73beiFvLhg0bNmzYsOEbZ7PA3vAdiRDiTfeKfi3fSreSDRu+o1in6iW9TgUO05YgsFQCgu2SUHfe13Ztf5ckDU0TnA05Sulgq8YuNa226LDz0VbKkSQNni4pMkwsbdgNL8VxizESPWjQoaGuQoJLOUo56EO7DPHrQScPBFGnSCdxSyXANAoVWGwjzzy5q5OEbDenaRTmdoo6XxDHncK2MiFu3QYxaxK21IqHwkPumSFaWD6xeCe/d3yZv3n5twHoy5IT0+OiPmE/6AbNYtEicZzvTamc5l2P3UYLy61mQusVc5Nw1PTPLO4sktvViGmddrZ8w7t8aPwyPdUNOcaixSIJRTfot3QxhY241XQuQ3erIReTKR99xwuksj5Ti++3QwoXUtiQhYmJpKG0mlmTshOtuDCYkaiWVDYchCco4VE4Kq9pfMDcJhw2AxyCW+WYpYnYTZYMgppHB4ccVn2eHN3i4fg+54MpobBoYbBrpbpFUbmQ1itObI/aaW7UE2oXUNqQSZjzUr7VDUo2XevAIKpIg4aDR2YATKuUxiveff4u0zplr78kDRoKExIrQ20D7uUDgsBC0r3e2W6OFB7rJBdHM46qHv2gojCa3EY8nByyHy7Q0rCyMZ+4+xhaWYT0LE1MaTXHTY9QGka6G350VhJGhknWKcHnd2cMw4rn631uypb9YMZWsCIUlnN6xhNP3GZuEz4/O6BxipdPJujA0ouazptadS07Ly8m3UBfYHBjwcX4FC0sSrQMVYESjkvRCXObctx2KY9/cHKBnSSnp2smYc4gqIhly1gXvHd0i8ppSqtZmrhr9xCe0mq+dLTHdi9nWUfs95b0dnOU8FgvyXZz8mlC1K9p6wCtHP1eyXKVEA8qrBf00prZzRHlFmTDirZVVGVIktZkew1SOvIyItQGMSkpDjOCYUO/V1LWIVWjEdJ33vPrxE2lHE4IiqfHiCvV2kozIul3HtvWScLYkOqWo7pPnDYo5TBGYesI30iqIiSalIgtMKcxSdI9x2nUUgUhIvIIIHhN69Afx2bIccNbzq/91KuDei/83F94C4/k9fGLf/XJP3FAzIYNGzZs2LDhO5+Ngr3hLefc6FU3jkC9/c/5rm1/a1xKNmz4TkQIsEbRSyvKOuxUZMAbiYj9WYiG9wLbSnTPUvsA72RnlaUtTRNA6GhLTVMpVH/dm9kGaG2wrUKsAyGU9ISBoaoSvBMI06nRUnqaWndBMq4Lx7CRJFyn/wkBRRExHuYcn3TJgzrulHXnBMl2QVXpbrDxXElbaoKgG9BsXMCiiSlbTaQMR2ZALFuu6GNSWbMfzPjL49/lX+WPsafnZLKmVQUvtzsMZMnvLK/xzvQOXyzO832D5zi1Pc7rKc5LblYTLifHTFTOh3svcKcd01cVrVd8IKtxXmKRa8Va0PoAhesGOn3AzKbEomVuUm5VYyJpeDy7w+PJHSaqs/10SBqvKFzU9XkDL+VbHKQztvWKHxx+CS265ykTrybbVV6TuwiLQHrH06uLtF7SUzW/df8RPrB1g3kb8/7BDVqvuBYecWE8pS8btHBUXq3/aWY25U47ZuliblYTtLCsbESi2rNUyZMqgx6Mw4LcRDw+vsdOuOLjLz3Bj159hj29QAtDKmtuNNtYLxkGBSNVUDlN4SJ+/fBxrvVPeHa2i5SeOGpRSd3190tHErS0TlG2Gt23DMOKz5+cZ+/c4mzo833pKzx05T5zm3GjnvB/vPBuPvbQF/jSYp95HbOT5DRWMRnmKOnohTVSeH7s4HMMVcGvHj1BIB378YIL0Ww9VNoyCVZMghXj7ZypydhLloTS8NnDiwTKcm68oLWK7SRnK+oU9985usL/p89zkM3o64pdvWQSrNDCsh10A44XIs1BMj1TqW/kExwC5wUX0tnaOrIL4jFekcgGKTylDXn//i0AbjDm5emYug5YlZq9fpcI2ZsUlEVEEFoao2htNxwIkEUNdRsQ7+VUq4h+VlGVIYHuqlAGSQA41x2LaRWy3xJGLUp6tDYE0lEVId4JemmF7HVKtPcC81CJALz3Z0ExWlvyw4xkuzhT/eX6OyGfJ4RZc1aR0r1ucDnot91wdWiojUIoTxBYhODV1NnXwWaBveFtQz/avB3/JAzigEX1+gcvNmz4aoQQPwT8GHAIeO/93/+qv8fAfwfcBh4BfsF7/5wQ4nuAnwL+AHgM+F3v/T/8o/b1wC2gtar7AVWOehEjSkXZSoR2XRuJEyT9bqHjrMI7qBqNMRJbK3RsaOcRelhjjcScxpi+QfS6FhRjFG2pmXsIgs7Zw8wimtiC8mTPRtgDi5+AGjTYeUilPLpnuwj20FCtws7pYK5ppCdOGmwRnrmQJEmXXNfU3XdXVXQDV5lq2O7l3F0MuLg147PLS/y2eZgf3v48+0G3oFZ4PpS+QCZaImHZkl0p/9nqHO/vvcJFfcJ5PaVwEVpYZjZjP5jx723/Nlo4MmHQAq7oUzQOh6D1kkPbo/Iah+ReO2ZqMrSwzE1y5hV9ux1zIZryp7aexyGRdAvFFsW9dsSpzUhlw8rGXIsOGamCv9B/mni9qNaiS4ys1y4sM5dgEdxot5iabgByHOQE0nJez6h9wGOj+3xv/wV+cNhwJZiihSMVnlAIGu8pvOCmGXGz2eJuO+KZ+XmeGt1garoB1tKFPJbe57jt8WK1zcVkyqqN0NJyPpqhheVy2J3A/PB7P8dQ1oTCYdfeHe+K7mARqLUDyonNWLqEv7j/NK1XlFbzmcOrbG8tz07wAmExUpKpzgvZIpnWKQ8Nj/nnL72Xd2wfMg4LLofHXNBTroTHPBLd4yPve54vlhf4nskrfOr4GmnQMFuk7I6XzMuYZRXxI3uf5x3RXc4HS+6Phpy0GXerIc/O98h0zX6yZCdcMlTlenG8IkoNhQsZJSUneUpjFFnY8kj/kAvRFC0sB/GUO/UQ5yWHVZ9npucZRwUH6Yye6tqJYtmyHazWJ2CK3XDJ0sZcX20zbVJuFyOcF/R0zaqNiFXnVOIQhNKghGccFdQmQACjfhc9np+kBFmLWrv+WCc7px1tWCwTkrDFuq7Nqj8qmJ728FbiHbjA0c4ioq2Sdhbj+i12FRBPKpyTFLWmXMZsbS+J065tbHraI123gbR1gGsVKjbIBye6eYgaVIjUUOUhdiAxbUBTSMTQo5POPUhKj8xarJWYF/q4g4pmPcDsG4WMDU4KvJPY5tW01j+OzYpmw4Y3yGsV97cD50cJi3vLt/owNnybIoRIgf8FeJf3vhZC/HMhxJ/x3n/iNVf7KeCG9/6/FUI8Afwy8FHgHPCL3vvfFUJo4FAI8S+898ff8geyYcOGDW8jNgvsDRveAP/1jz3Bdi96qw/jK/gnf+ODfPDnP/HHX3HDhq/NnwJe8d7X6/9/EvgY8No31ceAvwfgvX9GCPFeIcTAe/+/f9V9GaD96h0IIX4S+EkAtTU6U5itlSA8chEg9ytMrQjitivFWknTBIShQUpHlK4VpvspaEc0KhHSI0SnLOdA1q8IpKM8SZBZTRCtvbR9pzabc50Ca63Ef09FuC4hC+FZ1gohOnXT1oogsKhTTTXQ+MgRRaZLlgscznYKtzGKXtKlTuIEInBI5YmUIZCWflxjvOSR9JBJsOKZ4iL3w27QsS8rdoIFrexs/BSO88EU4m7ocUsWbMmCE5fSVyWtD9hSK0ay6VowgNxJWi9BgPOCE5fyv00/wLuy2xy2A6BTklPZ8HB0n9YrLuqTbgAOTywsSxdyvd3FesH1eo9dveCZ5QV+aPxFnJe8N7pNXzoUUHiovGLpQiyCpUuovOZXT9/L+XjGSdO1zz2c3qdwIQ/FR5yajPelrzDprxiIrjUiFp3C2XqYO8ltM+CeGfJcde7Mq3wnXqGEI7cRO+GS1ilOTUZP1fz47mcIheWj/WdxSEayYEflpOv71QLUgzei91gEWjhYt7tUPuDIDshd912u8CSqZXd7cfaerdugS+FULbEy3DkZcnXQ+VwXJiQKLIdFny8f7zLSJY8ndzgfdPaLE7Fip7eg8pqr0RFfKs9zf6fPOOrSCLOwZSdYnqnr709fRgvD0iWcmB6fzy/ye0eXUMKT6JadeMXFdIrCcbcekgUNdRRwtOjRmOArbBoPwlP29ByLpPWKaS+jcprb5YhPTa8SKst+tuB8MkcKzzDoFPJUNjzUO6a0mlvFiJ6uKUzIIKwoTMjv3buIVpZJWhIpQ2k01gs83fBx4xQisvR7JUp6atPVCsa9glUVMRrmlI2maQJMozi3M8d5Qb6MCUJLHLXo0FDME1S/u+xiQRI13WCxgKbWOA9J1FDdyRhenjO/OSTYLun1K4oiQkhHGNpuuPFeQhMH3ffEvYh6VzHoF13birKUNlwPO0pco9D9CvXYnLZVpHFDtG5tsU7StgpuJPi9V1ui/ji+4QW2ECIE/g6QA+8ETrz3PyOEkMDPAyvgMvDL3vvPrG/zNcuRQogJ8AvAi3RlyL/nvb//jR7jhg1vFuotsLy7MEr+yL/vvoWJkhu+I9gFXlsCWay3vZ7rLF6z7T8Eft57P//qHXjvfwn4JYDoysHGQHPDhg3f8bwZCvZ/BvyW9/7/BRBCvGe9/a8AA+/9310vnD8jhHgciPj65cifB37Te/8rQoi/SNfz9++8Cce44W1MuB5s/ODVyVt8JG9PfvrPPvpWH8KG72wOgdcmJw3W2173dYQQPw5k3vuf/eN2JgKHKQKEdAgBptL4vkUJD7UiGnVBE85KbK4x0mHvJrjLhmoVoSqBibo0xrbUpIOKtg0Q6/noxgTItFOuTaMIIrNOgJQ4J7v+7yZAJQ1CQFmG9LMKoTymCChUiL4X0sYafTHvlCvfpUjWbUBbaETQpTuaVpGLEGdFF0SxTp4MhOXL8z2WVcQXzD5P9G4Ty5YnsxtoYZjZDIvkM6uHSVXDOMhROCbBiqVNsEpSeY3G0qJofYDEsXQJS5cws53t3H3TuRmtbMw5PeP5co9RUKBwPBrfI5M1EsdAVmhhUHhS2XYBHT5g5hLumRG/evweEtXyg+NuePHf2v7XjFTBnbZ7XZZOUnvFPTtg4WL+z5P3kqiWQVChheXR7B7/6NkP88PXvsDjyR2atdp+UZ/gvCSVXVFj6UKWNmHhYpyXnNgez5d7bOsV0zZlZaMuVdJL9qMFD0f3eTi6z0jl9GXFSDbEwhOLTsF3gPUeJQQawZETFA9CfrzmnhmxdDF2Pfj5QOm9XY95drkHQCgN47Ck9ZJlGZFGLYsixlrJYd5jv7dk1mjipOFuMWAUlTRWMV/F9LZq3rF9yLOLPe5WAy4lU65GR+zrGVeCKf21sn6rmRAIx1aUE0wc22HOkenz+/kV3pPe5LyeEouWLVlwMTglkzXXkiNeLHd4Od+icYrPnl5kGJZcP93m8e37uLhLDd1Ll/zai4/zgQs3SVTL1eT4bKgxFi39sKLymkmQsx2tmLcJJ3XG504OaJ1ES8cgqtZ2fQUA47AkUS29oFNrh7qkF9Q0TnFjMSZUlkUVsZqljCYrjFWsrCKMW8LAcjLroYJORe7HXdUiC1u8F2T9htNFyuG0j2kUYdJijaKqdZfyGIbo0BBqQ1XF3bCzk10a5KBACM/R/SGkXeUp3s8pFzFbw5zlLCWIuvkIITzqXAFeEMSGsqfR0nG8Suj3up5xpRxx2DI96oP0Z/3h3ouuymYlSjnCwNDUAfLaChavv4L9Ziywfxy4IYR4P7AF/E/r7R8Dfh3Ae38qhKiAdwE7fP1y5MeAn3vN9n/8tXb42nLjpUuX3oSHsOGtJNaKX//p7+fiOP2m3P/v/cwP8bsvnfK3/+lnv+H78nzrxTe5yYnZ8M3l08BlIUS0/l7+CPA/r4UR471fAL9K10ry2+se7M+vtyOE+Amg573/2fXfau/9c19vZwJAQjvrKi+iloT7Bd4JoklJXQc4J/FWIEKLqQPYbmhbhdQOf7FES0cgHdmwpFynNNo8oJIh7TxC9duz65sHHtrKYa2gqUJcGVBLjz+McT1DpTUycMjQIIRHPLTCtcHZ4JSoJcYomtMYPaox62MMoxZjFEFosMLjygChHaUNOZcueOVkwhO7d3i22ONiHHIQnqKFYT+YoYRjN1hgvUQLQ+sDfje/xmmTsTQRHxi+wnP5PsEO+uAAACAASURBVFI4LsZTChtyJT7muO2zrZeEwnBezzgyfd6V3OLIDPhQ/zpu3QYRy3adctgtCI7MgAt6yvW2R+sVt5oJc5NQ2pA/PXmW1itGKicWLQqP85JYtnyqvMpL9Q7Prva4lh5ztx7y/sENjts+kyBnT8+JRcvPvefj7KgFWlicl+u2F0+L4J7pU3nNJ1eP8unDqzy5dYt71YD9eMGdckgeRpyPZ3yof51M1mzJnFS2TKRB0VUO5WveQQ6o1kliDiicp/KS/yd/nGPTo3Kdf/OsSUhUy418zEE26/y764RVE9FYRags07yrEH7g/E3aJiD3gnIWo7OWUFkaq9hNljx3d5cq1cioIFaGflbx8vU97NXO7/zGfMTzeoerg22Ml/z43u/wmD5kIg1PpS/xWX2ReZsg8WRBzf919ASl0dyth7wju8c5PT0bgO2rklh2bSQPFtovTrfIgoY4bFm0MXI9aOi8YH+04NMvXuXhc0fczEdnPuPR2tc6ki1SOMZBQU/VDHXJHTWkMCG1DcjbkOMi47rbZivNqW3AMOy8xB2CYO2WEkrLfq8rZBWNZntnQV6FBMqxnCco7VhVXZtGc5TipadIGtKowXpB3QZdKmSvwjrBirg72VUOpRx1q88W5q3p3IHmL48Qk5rJOCcLG+5OB0x2FpzeG7LKY0aDgnIRUzUanbS4VzLK7ZbeuCCKDEUeYa0kHHd+8KYKWJAwHhQEgaVuA5JhRRBYVvMEfSPCP1wwO83IhhXLk4zepCBcuxLV5vU7nb2uawohfk0I8bmv8e9HgCt0bR7/A/BbwK+sb/b1Sop/VDnytX9bAGMhxB86CfDe/5L3/inv/VM7Ozuv64FueHvz6F6fJHz907lvhJ1+xA889t3xPvnlv/7UW30IG77N8N4XwH8A/I9CiJ8Fnl5XFP8u8LfWV/tFukX4f0HXEvjvAwghfhT4B8BfEkL8S+CfAue/tY9gw4YNG95+vC4F23v/57/e34QQC+B31v/9V8BHhRCKr19S9F9nO6+5zWy9feq93/iPbfiG6X0bWgA+stvj+cPVG4qT3+m/vQYwN3x74L3/DeA3vmrbf/qayyXwt7/G7T4OvKHUJQ/otMEEnZqlRhalHFUd4ldhZ4lVBKA9GEE8rqiWEU4psqwiz2Ok9LRWdUl7tUImDgJPO40QmSGMWqoiJOtXaGVZrBLC0FAVIWHc0nbdHNieQUadYuZOImzsEJUkO1hi2uBsaHJKvxuAVB4VOJxzaG2IAotZq2BhaLGxoW0C5m3ctQT0cwAaFzBtU64XO2yHKx6KD7uyvVqRyYalS4hF27VXxEGXICdrJoOcdu1HLfGEwnSKsWyx62HAiVrR+uDM27nyIXOb0LqAlY14sdjm4eyI51a7PJwdEcnuJ3UYFGwHSwoXoXBkqmZmM2Y2ZWVjeqri6dUBj2d3OadnXJhMGamcD/Zst8/4VUFE4ZFrlXPpYiqvsV5ys93idj3mU0fXmMQ5obLspktyE/FwdkSqGp7qvcQlfUpfVqTCrJMgPVp06vQDhbrxkrmLWLi4Gwa0PWLR0PqA56p9jOuSLBdNTNGGON95KT9Qqp8+OsdsnrE1XnXpnoGhMkGX1NcGVFbTziLkVonQDnMao7dnVEZzvxiQJA2VCahsQBq0PLV3k6PhFCk8r8wnPDw5Zlqn3FqNGEQV//f0Ce71bvC96XUAjFcEvqu8zNqE0mgknonO+eTpQ/SCmkS1HCRTeqpiqEpCYUhlQ0/VjNOSWZ1woTfnuOwxL2OyqCGQDiUd3//wC0x0fnb/p02K8ZLfP7mE84JHhkdEypDIhnvVgHFYEErLrElQQhIpQ+u617RsNXkTcnLawxlJEFnipCGLGrKwSzgMgy75tG0CgqShP+y8s50TOCeJ93LKWYwQnukqxVpJL61Q0lM2ml5cMzcSPw+JDxZrL2toi5Awa6hLjfcCvV+glKMX1V0i43rwEOGJ1smpwZGm7Gm8BzOwRGs/ayE8fhbiQ0fvXOcTLrXFW0FtFMUiJh1UlMcpvb0V3gn0uxaEQWf3KQWYvqQqw67tRHqQr7+K/WakenwCuLa+fBm47r23vFpSfDC8GANf4DXlyPVtPrK+Lq+9zVdt37Dhu4Kf+TcfP7v86z/9/XzmP/8zvOdg9Lpvf21nE4KzYcOGDRs2vNW8GbLefwL8fSHEk8DjwL+93v4rwPuEEP8VcAn4a+uFdyGEeFCOPOLVciR0NlD/jRDiUeAh4D9+E45vw4ZvGz7y8PbZZSEE+8M35hDyWqX+n/yND3J565vT175hwzdCEDic9UhlaYuQVnjiXoOPW5pSk2yVVEWIzgzVPEL3GpyTtEZ1ITOhoXhlQHp5QX+S470gjLpBpHYZIvsePOR3+owvTfFWINcWfEnUhUs4J7GBIutX1HVnxZdtFTR1QFlE+MMIda0kUA6hHFpb2rQLn5GBo641WlmkdDS1Js3WPZ63Yu5tD7pBuDzhoD/jYjJlHBQkqqX1iuvVLqUNuVG8g3cP7vBisc27+3fQwmK9JFU1SxMTC3PWP9tXFTObcrcZ0VcV14sdhroklQ3tOvBFCs8rxYShLomkYTdcci095qjp8eSgS+A7H3aBJABLGzO3CTfqCc4LfuvWw/wbl79ELFvuNkMeTg95JLpHLFq0sIR0t2tQWC9xSA5NV5BWwnOnHfHl1TnulgPuLgY8sXuHSVhw0JtRGM2HRy+yEywZqRyNJVzbFabCEArH0mkaL5nZ9CwQp/IhhQv5zOwau9ESLSwLk7A0EZlqKK0mkJYvn+5xvregaENaJ1lWEVnUUDaaSgRoZTm3Pcc4SS9s6OuKympqG1C1PU6qjNH5BctVgm8lyV5OpMzZ87qVFUTKcFplXNq6xaXolMvxKbFs+St7v9elbLYTnlleQAvHSZ3xZXWuC/3xkrvLAVUbMEgqhlHFuXTOJCx4Z3qHXlBT2BApPM/Mz3dqt7CkQcskzFmaGOcF0yJhEnfHJYTn7tGQa+ePOchmDHXJls4ZBgWPxi1z2333302HZ1WLz80OCNdDpJXRzJuYygQMo4qiDTnf66zzpPAcFxmTcZc8WbcBk6zg5vGIU1K8k5hck04KzFGMPTCEgWE5yxiNcso8Iu61lKLrjR73Cg5PB0gBobKUaKbLlDhtqDuXSbwX9JKaYhF3w4+xoTpJiAbdQOJJnjKIa7SyFFWEjCyxNngvEJeKLp0xNLRhSL2ISMclTa1Rk5okrYm1IQ5avBNkg+4znw0rwsAQX5hRNRqpu/RHrwTGdXMXg6xivkqw0wSGDUHvD7mQfv3vuW/kSxLAe38b+Imvsd3ROYx8rdv8oXLkevsp8De/0WPasOHN5p/95If5q7/0GT50deutPpTXzZOXRgxi/VYfxoYNGzZs2PBdx7dfY+qGDW8BH762xcu/8LFvyn3/6cd2+JfPHn1T7nvDhrcdXqADS3W7hxs3JIOqcxCoA0b9kuNS45wg61eUZYhKLFpbwFJXITrtrMOCc8WZKi2EJwpbilVEOOyik4XyJOdW3S69oKw6p5CiCglDg1IGGwuiwFLXmnhckYQt3neBFn6npjGKug3wTlBXmiTtQi+KVYRf95rmZUiWVRgrqYoQebGkbDVXRyc8kycclb21aijYDZdEsqUvK5RwvK/3CoWLuBJ3wZd3mxFTk+KaAS/nWxzmPZ7auUmiGiJpOG0zJJ5Zm3AlOaFwIa1XpKqhdYpIGi6np/RVhcSjpaFymv1owdSkjIOCI9OndQFKOF6ptvjk7au8f/8WEs9PPPKpzsFCdCrdmdLtErQw5C6i9QGv1NuctBmRNHz6+CqVCdhKCiZR13Muhecj519iK1xxTs9Is5pYtozWcfCvZeliZgisl3y+usQzywvshCuenl1gJ15xWqfE62CTl+cTQtX1/o6jglk9pKdrZk1CFjZnkeCRbAmkWzupPHAbEWhh0cKeOZxYBLXTzCcJT08vIKUD4eltFeTzhHDHYpxk1USM4pLSaIpWk8qGpY0ZBgX7wZyH9BF7qqGOb/KD2Zc4sRnPN/t8Ib/A55cXuZScstdb0tM1XzraY14kPHr5kJ6q0cLwUNTFfSjhORfOeLnaJjcRnz28wF5vxbyOsU52ynLZQwrPfn9JL2rQ0nJU9Zg3MXkUcRBPOQhP6akKhaOXVMSiIRSWS9EJrVfUTvOZ2VXeP7nJzXLM7798Ce8Eqe56uqXwtEaRRQ2juGRRd5XU3dGKvA4pqpD+zopBXOPOScoipDepkYFjVUTIwKGkR51qkt0F1nXBTMsiIuhb6kqjAsc4KzlZPy6lHK1RjCY5qzxGa0MdW6yVFPOEywfHTIuEqtZEUecSVNQapbrXzDnRBVfVkmwv78JplKNZhWTjJSeLjHSr7dTrSmOOY9JLXUUjixpWRXzW073MO5eWOOkqIN5DvJfT1Jow+hYq2Bs2bNiwYcPrxZtuQEpu1wTaEGnTJcK5biQoG1S0rSKQjn5WIWXXzlFUIWlWIei8q6VyZwlrQngibegPSlrTtUuEkUEr29npxZ0HbxS1uGeG+PfM0crSzmKWsvtxT6IGYyVN3Xke13VAvd7naJLTGEVVaeK4RSpPWwU0oUGpbgFnjEJISNKaXtR5/076OTvJil7Q8Oxyj1mckqiWx9J7WAQTtaKvHI0PiEXD5eiYg7DzbL4QzWjH6qxl5Iur81xJTlDCIfHdwlo2KOG6BR/dIkgLS2HD9UIq4E45xDhFqAyfrS4SKcO5ZIEUntopPnb5CwyDkp6q2FKdf3LrFVI4chfydHmRo6aPxPP06XkeGR5Ru4BnDs/xl64+zVNbN0hVQ09VXbuHrFHCn/lua2HOFtWV1xy1A5YuZmVjKqeZtSmnTcppnXZDbcqyaJKzhaPzgqM847HJEU9ObjFUJamqOwvAdWuMFpZo7bVdO40U7syuEDhLynwtdj2C9iDF8NPtVbRyDPsFzkmirOkGS2W3oM/bEIBhXLGyER9/8Qm+7+KLkMF+MGdPNfSlYChbzqspF4IF74jucM+M+PjRk+zFS6ZNgvOCnf6K0yZlKWJWNuKh+AgtDDvBkivhMalsKFxIJA0vrrbYSgpeno5p24BAdUONo6jEekHrFPMqJtUtXz7cY2+4zbX+CYlq2Qq713Mc5PRlSSwaMumxUvADk+fQwnIxPuVd/bvULuBWNeK0zgDoxzXWC/I2pDIB0yIhDAyBcvTSCikgCkyXqniUUPQ0ArrPg/dUbQDnK1ZF3Flwxi3WBizLmEBbylkM/bw7oTWKSJuzhEVrJFFgsf0KYxTZqCTVDfGg5blbewyyiniYEweGmy/uIPstbR6wczDD7wgi3VI1mjA0uOOMZvfV4c0HJ+WjyzPKOsRaQSDXrSFOEGjLoFdSNZpAOlqryJIGs/bIfiNZc2/GkOOGDRveJK7tZG/1IWzYsGHDhg0bvkE2CvaG7xr+JK0Yn/g7P0D6TfLn/lrEWvG//rtPcXX7G3cD2fRfb3g7okLHqowYD3OcX5djpUcFlqO7Q3pbBW0dUE9jdg5m5FVIcZwSjasuMCLoVOkobs9CZtqjBHOlIVCWvIjoZxU6sMyWCb20xrQB/oG71uMr6mVEstVC4LBGEaY1jQmo6846cHWUkUxKaqNIw5ay0QTKUQNtq/DAeGuF94JAtcwWKUI6VGApi4gqajipMu4dDdlLl/SDioGuiJTBIXh6dUAkDVkwQuF4brXL5fSUsS7O1NhTk5HKhmFQUNiIC/GM2gXULmBhEo6qHj3dpettRzmLNmbRxnz5zh4fufoid/IhSnaq7SQq0NJiQsk4LMmCGuclg6BkW6/O1N8jM6D1iuO2R6oapm1KL6g5iKbdU3fxzjohsOFHtv+AWLQ4uqCcB0OPD7BenqUoLl1MYSOmJuUL83MMwoqTKuORwRHHdcZQV6xMxCO9QwZBxTAouuRGVawVe0e4TiZ8oEa3PsCuW0scksarLrnRxmhpzhRys66M9IKa1nWqPsDCJEjh0MKRqIYrg1M++exDbO8sOb3fJx5XNGvbun5Y88LRNlncsJXmfPreVbwXvLDY4aTOWA1j7kX32Q/m7KicVFj60pKK7v+j/ZzfmL+bL073uDo5ZSdacVT36AU1L68mfN5fYCdZ8WjvkEvRCW5twbgfzZHCYbziUtq9BrkNeW62w6xOmBcJh9WAJw5usxOv2E5WvDKfcFsNkcLzgt9mXnfq9l6ypK8rtnTOWOdngUAKT19V9BWkqmEeJSxMzLlE8vx8h1BavG6JA8PJKqUqQgaDkuksxT0IX44c+SpGh4Y0rpldn5BPFOPxivkiQwiPMYooaqnKkDhpQMKsSGiKkDBtCGJHtB5aHI2674a61uAFadxwWqYMo4rtrSWzRcrl3VNO8hRiSxS3+MgghWeYlZzMM6T0eO/xBxXTaY+sX9ELuyHJYy/OrDuFECyWKVlWsbjXxySGILAEQWfvORnmLIsuECfLKvLi9VvhbhTsDd81/Jc//M43fJuHdnqcGybfhKN5lTj4ygX8D75jj6vbGyV7w4YNGzZs+HZlo2Bv+K7h7Zo4vjfYhMNs+O5BrAeSwsBwssiI1hHEZRmSTUpW0xQ8ZDsFeRV2fdDbBW2rSONO4bJFQDZe0raKeh4jBp1tWdVo0rRGBxZjZadkK4etFePtJfN5Sq9fYVrF8eGAsN+QJTXGyS5cYq20MagJAgsx5HUXMmGMwuaawd6C6Z0h4WiF84JFHpOkNatFdyIehN0xrpqQi3tThmGFcZLdeMkwKDmnZ+zrOQASh0Pywd6LNF5ROc2NZhscbOslrQv4Z688xUf3r/P8cpeDdMbF+JSL8Sm63ymQD/qlH/Qjf2RyHS0su9GS0moO6z6RNATSshOvaNYq+N1yyEBX1E6zMBFKeBLVMgoKLkRTRqrgagQX9cnZfbc+oFlffjAIWfhu8DF3EffbIYULsV5y0mY8t9hlEhXd9UyIQ3Rx2/GCy+kpQ1XykcHzbKnVuke4ey8oPM1a/3sQu97tX9H6AIdk5tIz5bxwEffMkOeKfb4026Mf1tycjRDCY51kkhXcnQ6oTxPSnZy2VYz6JaGyeOB43uO9F26TDiqmi5RkUiKlpzS66/N3kr3hktYqTsuUh8bHPH+6zc2jMcMLJR+/8R4emxwy0BWBsFxLjngivslIlsTCsiVzzFoND4QlUS2xapmEBQ7BJOyeo8/NDnhB7zAJCxLZsLIR0yYlVi0H8ezsM6SlY1mHTLKCdNRgvKKnahod8Mj4iPcNb5wNqD5gZbse/cpp/vFzH+b9525SWU2sWiJpGelXh4aV8ChheWhwzNJEBMJhvGQQVRwnGbvZilHa2edNiwSdtrTziORc2YXMXFzivaAxAcNBTtVo6iqkOklItguqMiTq1ZRFiAi6mHStLMsqYhDXCO1ZljGDXkleRt0gcdSQtyHheq6itYrGBEy2u335tepf1CFaW8J1ANR4mHP6/IQ6NITKUhlNWUTYPMAOHU2h6Y8LkrClGq8j02cpQdySpTWtUbStIllfPgu6eR1sFtgbvmv4blGF/+Ffe4pEf+vaWjZseCMY0yW6tVZ1ZeOwc9iwS43OKuJ+jRCeXlxz//6Q3qgkX8QEkSEMLEcnfSb7cwLpCENDtNMl83kvyOKG2TIhkF25+XjaZ2u0ojcuEMKzNVmxKiO8kQwmOctFQjpcMS9jpi+NGV6eo6MGnTpmq4RBVrEsYpo6wLUSlXY/rnuXTllVEb24RinH8n7vzLt71C8Zxd3iwyHYDlccNz0mOudONSIShvN6ikMykBWxaGnoPq8KxwU9PXO4sF7yzkduY73kA9nLpLImFJZmvdBsvaLxili2tD6gcprCdSfsxknuVQO2o5xAWE6bjES1lFYzrVMGumIvWpColovxKQfhKX1Zrhe7DWrtvlF5xYnLukWtTbnTjmm9YhzkzG3CK+U2WVBzXPe4X3We2OeSBcZLlk1ErAwP9Y4Y64JL4TFbwYodtSTEkUpDLPxZKb32kPsuybJwEbkPzx5X4xWntsdx2yeWLa+UWwyCEik8zy73kHQL4tYqahPQj2saq5itQg5tj3G/YLA15eZ0hHeSqg2QwnN4NOD83ozDoo8QsD1asSi6BELvBdYLtpKCVRNhvcA6wXaYc1OP6G/NGYcl7zy4x5eXexifIvEYr/js4hLn4gXvS19BC8th3bX9LduYW17ywfHLHIQnDFT3HpjZlKaveKne5X4zwCK5mY95cnSLW9WI+/WA1ksOyz6jqKQX1oTSsBUVfP74PKOw4G4x5FI2PXNL6cuy8xpX5Vd8Bh99512WLuHFcodEtdQuYNZ2vtk38xGxMpxWKb2wBqB1Ci1tN3gcddsy3XRuI06ipGMlPIFyHN8bsL2/YPaFLXrvPkYrS9VosqyiCbuT2NGgYLZMiOIucTUOWwScvWZZ2HBcaXqjmukqZLK7IJCu88JOKvTzCWarG1SWArKo5iRPCZykbgKMUfSTmryIWPmIwbUZbj2wWVuFM4Kg19IeJZBaonUqZZbURNp0HtlJQ90GDNKKhRMkYUtRhxS3Xn/75maBveG7BvFGxn+/heytw2T+wV9+75tyf3/2nXtvyv1s2LBhw4YNG/5kbBbYGza8xfzkR69xcZzyw+8591YfyoYN33SU8izzmCRuiaK288CVjmSrJIsa7LrUGwcGqV2nZg87RVhJRxgb+lFDZTqlanewoljbbzkv6KU103sDLlw6YTTolOswMGjliIN1C4JyeGBrsqI2AVtZwfDRiqLRNCYg1hVhaIgDg4kavIewZ4i1OdvPKC2JAtNZeTUB2/2cKqmJA0NP1zx/ssPjO/epXcB7+zdxXvJIcp/WB5zaHv96eZX39V4hkzW5i9DCsBsskTha5JmCnYqagohMdsph7iKWLubU9KhcN8icqprWK6ZtxsykhNKgheVqdkJfVbRecSU+ObP208LQVxWZrJE4Mll/hfe1xlH4bnnw+9UVbtRbTIKcwoXcqUcs2i5Z8KTK+MDkBoUL2YsWfGj44tlxKhw/utWuUyC7531Ldq0Q6TpZMBWeej18unSaQ9vj+WYfheNT84cYBDWl1VxfbDMtEh7bPmQ7ylmZkFmTsgwiXlmMOZctuJsPeGh4wvmss/fbSxdUVnO+t27HEZ7ChDy8c8yijsmbkH5UMzw4ZF7H9MKa/CgludAySKvudXWS02XG/8/emwdbltz1nZ/MPPvd377Uq726eu9qdQtJjcQmgcCywgPGYGLkgDEexczgmYAZ2SYI8GAPg8GWw4EdMTEQwx8ExIwjGMaAzCJhjGXtaEUtqburu6trffXW++5+z5o5f+R5t6vb3a0Gtbq6qs4n4sW795y7ZJ6T99y8v/z9vt/FcMzOoI7v5iw3hoQq5b89/vGZnvlO3qShYrp5DW0E16ZtduM6ocr40969SKFZCQZ8ZWuVJHPoipDvXpzgiYJFNWDDmQD7SKAfXGGoPfZ1jR/oxFxMF5DCcD1uEaqM1WjA5VGHBzqbaCPYnLboBFPOHywRODmhyrgYL6CNYMUb4MqcRTOkIWMCmeJSMO+MaJqYhrSRbY2kMJK9vMGiN+TiZJ6HVq6yn9aZFi77SY24cBgkATuDOhudHuPMw1UFDS+h0NJK2RUStCAvJM7JEQ0/Ic4d2rVpmZ7hsHfQwHdz1uf79KcBzSieaZv3JiGRb3XuhTCME4/G/Ji8UFy6Ns+x9X0GsY++Z0RaKLtakTnUPBtN95wcz7OrYknmIKShEcW4quBgFFFoSeDkRI2EepAwDlMmY59x7KF9mCYeQhhqUUIjSMgKRVZI6vUYJe21KFwfveprXTXBrqi4yThK8t6H1m52MyoqKioqKipeI6oJdsUdxSPHOnz+0sHNbkZFxR2LMZBNXeaaE8aJR/yFOVpv2eFgs4VsjDFGkGUKHQpcL2c0CGk0p8SJw4AyH9oIpqlL4GUMYp8kc2iECbubbbxmQmdlQJI7OKpgMAnQWhIFCWlu85Nrfkp3EBE1rQRf3TcUxsp1AYyHAUGUMox9JrFHLUyIUxflp0wSz0bqguej7VnfRy1o8kLSzwIWwhG+m7M9adByp8ypEU0Vs6L6BCLHFwXn/CuMjctQhzTUlMJInk2XSLRb5tDmFEh2siYdZ4zC0FLWKbEwkmPe3iwHW5XFaRtul9i4RDKhJhNcCjxRvEDODqAoS75dilmR4lCHDIqAq+k8R7x9Ptq7m2V/wII74oRvjVDaasKj0XOzyGdsXBvFxaAw+GVhXYYkKwswAVIUE+2TItnMO0Qioacj5tWIi+kie3mD62mLrbg5K6gbZT6hymi4MWfb24TzGR1nQmYUnsxZ9ocAnIz2ZtJ7b2peJpIJQTubSfppI2c564fmMol2iY1Dol32sjrj3Gece6wf28eRmt1hjaKQOI4myxS70xquUzCJPbKaouVMudu7TkOmtGRBEGzT14ZrRZ2hDqAJf9K/n2EW0HBjhlmAKzSPrl/mE8+e4szaDntZg2tJhzRUtOUVGrLAE4JFpWnJKUeY4glBZhSnvB2+4J5gO7OR8kzbosbMKHKteOvCc7TUFF9mtm/aZSdrsJm0uTppA/Bo5xK+zAhEXprYZDMjIFcUKKHpOGN8mc2Mhwoj8aU7K4DspjWafkzkpBzEIcPYxy9XddJcMR35NJdG9nM5CCm0JM0d6n5CfxrgOQWenzGe+rTCmCRz8JyCUeKhpGGauER+yv44QipdXi8ErpOzstJjZ1BnOvSJmjFSGJuD7WrGqUf6pQ68dYtRL6LenuA61gE2cHL6UysF6qucnVGdLFNkbmlSJQ15LhmkkZXZTDxcpyDTkkYYk+bKFjNPAoSwhlKvlmqCXXFH8W9+5GEe+6X/eLObUVFxx2IAL8psWoiXMT3XIyskbjtmnLp2gp06dMcRUhqiekJeSHw/J556eL51fjzUu9ZGEE88W6C22ifNLxD8cQAAIABJREFUFXU/ZbvXwBgwpWb2wUEdx8vx/ZxCS8IgY3urzcLSwKpDDGroQuB4OY5r3R0PbdWNEUwPrEpIMnVptSb0BhFaSxAGf87ao2eFIkkcJrldPvdkwclwj/PxKqeDbebUiEhkNKQmMJoWGbGM0eWE97jbnRU4Hv6PjSIzirH2acqYSGZoI2YqGzeijWRsrIqHV1qCayOJjUtmHCSaXhERG2+mKvHMdIlQpgzykDc3n+N0sEUgMn544TMA3O0dIIHDaYUSgtQYNJCV6R2HE/bCCBKjGBvXujbmzVlx4oXpIkvekIMsYjtpUnMSUu0w5475/z77KN/3yJdZ8MaEKuV63OJ0Y5dztctIrOV5TSa05YSayHBLN8tDPKFxF+3tQ/X/2IDm+aLJAlEeTzsBnRifWLsc8brE2uWLo6OcbO0xSEOavlUDSbVDVlinUIAsV4xTOzntaftjrCGnRMIlUtCSY2CMKyQPef+JoZZcyOe4mC7yoa0HOVbv8v6HPs5nDo6zmbTYT2xKz9V0nmW3z3Fvl4aM8dA0ZIbGsOEMiI1izT3getrCFQVHwy6DPGBaePTTgAVnxJp7wLwaEcmEhsjQs/4qYuPSLer2XOR1ChPwx9v38Z7lr/DJ/ilyrag5KbmRnIl2mGjrBDrI7RjxpZ1E+yrHkzkSgxSGRpAwSV08p8AYYYtFe7YI0A8zJpnLJHGp+wnTxONg37MOmdIwiH0aYUKSOSSZg5SGRpSwtdtCJwpSSeIY6otjhuOA+dYYKQ2OXxBPvNlzfTdnOPXwH+rZwuP2hOFOnfaxPXZ3mvhuxmTik49d0saISWzTQMZTn9DPiJpjtnZbmK6PWJ7gOBptBP1xSD1MyAvFdOpRTB06i0PS9NVPsCsd7Io7CvkGLXT8RnnXPVVhY0VFRUVFxRuFKoJdUXEb8Kt/5xGyQt/sZlRUfF2UMNSjmDR3iDPHyu05BXPNCXsHDRbnBoRexn63juvn1IKY/b0GtZZNS8gzxSSxkeWsUCzUx4RexnDqz3SPAbLtEH91gvIyG00OMtKpi+cVpOUyb9Sa0h+G1GsxtTBBRDGDYYQXJGht5QSlgGnqgjLUghQhDJFnl7mDsgBSSluQlcQujluwOWhy7+I2j2+tcuRIl/u8TT4xPc3vHbyJjaDLA8EVMuPQlpOZRB9AUySzdI/DKHYgCjw0NWWLELURxMZhX9fIjIMrcgJRyvQZl7H2bZQSgSsKnp4uo41AG4kvM1b8PltJizfVL+GKnIfCSwQioyYyfFEQCI0SNhJcADUhycpo8VAbXAy7hQfA2HjE2qWnIzxRcC3rMNEeV+I58jI9pOHEjHMfX2b80ea9nGrtWU1lJybRDifDXT74Xf+WthqzokYEoiASNlJeFy7qhqCIg+IwRq0xSARKlGkvRnOgp6gymh4bTWoku0WNmkjLbS4DHcyi2EMd4oqCzDjcX9vkz/bv4tnuPKfm9gmULcT0ZFnIqhXxxGOpOWJUBPz23psJVcbbms9wxtuiLVNcDDVp339R+SwqWFFd7nb32Jtv0HImtNWEdy48SaJd6o2YeTXii5NjPBsv8fjkCN00ItUODzauccTbp60mZMZhv6jjyoJrSRtHahLtIIVmORrSL0KbGiNTIhICoXFnhy0HEo47IwoD+BAbybsbj9OWKd9ee4qsXPnoFnW2shZZ1uLZySIL3oiPXj/N3XPbHAl67MR1JrnHVhJQ81ImmUvo2RWVufoEVxWsdIZkWuKGmlHi0alNiXPrpDq3MGQ4DqiFKTUvoze16Vu+a4/1JHGpNWJi10UpM3NfLXLF3kGD1fk+u0UdFVgZzShIyQo109IfDkLm50YE6z3bhiCn9/QczvqEaG5CdxzRrFmt8+W5AdoIXKlZX+qx49dx3YKikKSJR6s5JssVg/0aSIMYORTzcvZer4Yqgl1xR3GjPvTPv/eVnR3PLje+2c15zVBSEFTa1xUVFRUVFW8Iqgh2xR1FK3Jnt7/trsVXfOyv/Mi5b3ZzKiruSLo7TTqLQ2p+Ss1L2RnavM2V0jyinzkEUUqrNiXJHIJ6QuDm1thFGA7GIZ36hDhzyLQkyRyWmqOZlNrBJEQuJGgtaNdj8kLRiBImSuM5OZlQOFITeBl9EzKa+EhpODZ/QF5YixVjoOGn7A5reE7B2lp3JvOX5A71KKY/jGg1JqS5Q8230e2an+KrgvWgR2tjavN8nZzvrj3Jk+4+vSKaFRT+/vBhToS7RDKlJhO+ND7K3eF1AIY6IJIpDTlFI2mrycxw5XOjE8y7tuAxM4puVuNEuFtGY60UX0tOUcLw3vYXyYwzK/rzKCCCQOS4QtOSxSyXWgkoDIy1RAlb+HlV++wUDZTQfGW6wTFvj0+PTuHLnJ2kwfa0wWo4wFc5mVaEKp0Z3JwId0m0y6rXIxAZ7zh1nrac2GirKAhEgYshEOAKQUsGuMIGCgqjZ9Fp288CjSEzBRkFmdG4QnKYij3RBV/LWigMUmi28hbDIuRPuvdytr5NYSS9LGKvNNyRGC6O5pgPxowyn/csP44Uhk40ZXtSZzEa051GLIRjHGFzkE+t79Lypjw7XmQvruGpgq34YTxZEBcOD7WucTrYLqX3+jSkpiYkLSloqJhRETApfOacEctunwf8a6woW2DoipzPjU9yrnZ5tgLxbLLM1WmHRDs801tgpTYk1Yo5f0JuJC13iiM0H987hacKjkYHnAx3Oe3bPPqaTMpVEFtYq4Qpo+yawKTUpCAydkwXpKyrEWfcXXra51rYoSlj3lp/lrYaExuXu8NNPtK9n43aAaHKuDppc6q+x15S5/q0SdOL+erOCq0wZm9Yoxak5FpS81K2py5RkOL7OTU/RUlNkrhIaVhsjBinHoURBG6O1tI6O45CQj/j6HKXQeyjpKYRWcm83igi15LQs/UcvioI3Jxx7HF07oBJZus1Fu7fIteS3X4dpTQ1L8Wby9m8NoffSDg2b0UPQj+jt9NgfWOfNFQUWuC7ObXOlHqQkM6rmdnMq+UbmmALIR4Bfhr4HPAW4F8YYz5V7vsHQBPoAB8xxvx+uf0c8BPAc8AS8AFjTC6ECIAPAteAM8AvGWPOfyPtq6h4JU4uvnpHpoqKiteGQkvmlgaErl1610YwGfnUGzGha5ebm4F1c5wkHkpqFhpjfCdnmPjU/ZiDcch8OOFi3EEKyApFy4vpuwHztQn9OMCRmvHExxiB7+RMy4KoVmg1jneGdUaxT+BlFI5kGruMM2+mw6tKvevDifux9pi4cGZ6uHUvpde37rCBm88m3wCBkzHIQ3bjOpf9efr6GUCw4vRpqwmByIhExCP1i6y4PVwKApmx5hzQ0xEKw5o4mOkTFwj28zoNNWVeTXl3+3EKU6bClGkiSmhrMW6ULXDEpoy15Qtd/A5TT2LjEBsoyBhqj6G2RZxbeYvNtENDxfSLkM2kzZrfYy+rs+QOeSJe40y4jSsKTgU7NDtTAmm1rq2iiKZAotBWnaJUGEmRM/dGYDaxtm0CjOFAx/hCMtQFiYHUSDIkCkNP+/aHiQ7YztpsZ00W3CGuKBgVAa4o+OpobeYq+bkrG9y7uk3Hn/DseJHrkybdccSpuT2G2jpMhk7GIA1oejEHeY2lwGocjzKf68MmjrIT58DJ6E1DNpoHNFyr8930YnYmjdJRsWCYBfzp1lmutjuEKkUbyaI35OHoIkedAy7G8wCEKmM/q/GWxrO4aFwEZ90dNII4vMopd5fYcxgbj7acslVrEoiM4aL9UfZsssxm3GZauDSdmFQ7vGf5Kyw6A3pFxBdHR+kXIbtpg2cHCxypWYv1u2rb9gebsqo2Xun0aJVECtxy/IDVQl9x+ii0VaQRKZlJcZ2Ch5pW0z0zii3ZZM4Zz8aWRnB2YYevXF9lqWUdVsephyM07Y5N5cpjSZI7Nm2rdHY0RuCqYjZ5XaiPubLTYa49JnQzfJXT8AVpofBUQehmbA07tFasvvZCOKIb18rrh3WezLRkoT4mcDK2hw3W5vqMEp/ITRkkAceP7pIWCiU1B3FoNfgX7fmP3IzAyRim5aTeT0iUbfP+4NU7Qn+jKSK/APzfxphfBn4T+KcAQoi3AN9pjPk54KeAfymEaAtrpfdbwM8ZY34R+7n60fK1fhK4bIz5Z8C/An79G2xbRcXX5Zf/5gMvu6/mVQs8FRUVFRUVFX95vtEZxDZwuM6+CHy+vP3XgU8BGGMyIcQTwLcBXwVCY8xW+bhPAO/DTqbfA/xM+ZzHhRAPCSGaxpjBN9jGioqX5YfffJT711u8519/HLBqHP/hiW0ANuaim9m0iorbElcVViLLzfFVzjR3meuMWW0MyLVkkNjoc83LKEzOdrfJfG2CxLC93SJYz3GUlWlbaw44f3mFB09cRQpNoSVKaBaiMUnhWK3dQnH9ySXmTndBWHkxicFRxazQajwKOLu+TaYVuZZIYRinHqGb0fEndFWEp3K6cYQQhvV6n4MkYmPpgEtXF2jMjan7hsDJGcQ++LAdNzhe2+eeYJN/s/cdnAm3mVc2QhbIjLH2UUIz1j6eKKzkH+CVGthg3RCjUlv6cLkfmOk6Z0YhhQbjEJea3NpIemWBYWw8dosmCk1abtvOW0Qy5XrappvVWPSGZFpxNW5zKtpjwR3SciYk2mXJHXBPsGkj5JGNcEo0TRkjy4in+6L/qZEz2cHYqFn0OjYuXe0TmYReYYsiA5ExNh77eZ3MOFxN51hwh1yY2mlFZhRNx7olFkbO3AwzIxnnPtdli6f7i9w/d50/u3iGh9ausZvUmffHvOvUeUa5jYg23RgiWAxHtNwpwyzAlzmLwQhP5kwLly/0NniodY1BFvD0/iInOl3iwuHC9gJ3r22z2hhwqd8B4G+f+DyPD9fJtaTtTfGljYYfr3fRRpAbxSeunWC91WeQB/SyCI0g04qmGzPIAjaDDtpINp0BDWndNhedAQWCQOREMqMhchpyn0AYoM9YS1acPl9RG0ihuTBdZM4dc29wlUU1RhvBcW/PyibWIG55pUSjItYue7mtKzqUJXSFxpcZT4+WaHsTHmhcs+kkMpuNPyU0Eo0nCsbat7KP2uUgj5AYLkwXrDxk4bE7rTMfjHHdgrqXsDepzRxYW2GMJwvqbkqqyxUnFRB5GfvjiIX6GGNgpT4kLRTznRF5Ial7CZcPOizUxwxjn0aQ0HBjpFvQ7dc4ubxHoHJb1Cg1zSDBEZrIzai5KTvjOu1oihTGFjfWhxjAkZruOCJw7OrTOPVoBAntYDq7BmgjGGw1aAQJS9GQq8M2oZ+96mvd151gCyE+DLyUBtg/Bn4W+LdCiLuAtwH/U7lvCXjihscOym27wPAlth8+56X2/RcTbCHE+4H3Axw9evTrdaGi4gX87k98K5++sD+7f99ai7/2wAp/+PgWS03/JrasoqKioqKi4nbg606wjTHvfrl9QogvAD9hjPmUEOIB4D8IIVaAHeBGCYZmue3ltvN19r24Tb8G/BrAo48+al7qMRUVL8e5jTbnNtov2LbctIL6jaBKC6mo+GZigEaUMM0clqIhi+GIXmrzfyMn5Wq/xdF2j1Hq4zs5tcjmvCqp2VjrkmtJJ5qSG0mmFUtLfRxZcH5/kdWGjdHU3YRBElBzU/rTgPV7timMYK9fpx1O6U4jPMfmbraDKftBxEIwYpJ7PLGzzEMrm3RlRNOL2Ry1rAOdLIjclFHq03CtSYrE0D51BY0g13IWNQcbNc2NIpAZ90abNhqmQ0ZFQIFgVAR8eu8E37X0FF8cbHBPfYv9rMa636Ob11h2B2xnTVY9m0N7mDc9KWzk++N7p7irucPmtMW51lWendho5iAPbVTaKDrOhL60UnS6zNledIbEZeHhqteb5dmeq12aRc8LY1cCAGoineVtpzc4M2IUHgVj483yrWPjWsfG0txkM7MR30S7XInneGa4QL3MYQ5UzoI/4oneCve3N9lOmqwGfbbTJjWVoI0gVBlKaCalLOBhtPrSaI6FYIwjC862d9ictDg6d8DJaA9f5mgEHWdsc8LLfqTGwRP5zLjGEwXFYS5x3gJgL7NTkG8/8gxP9FeYZC4biwc8fmGdd9z9NBeLDov1MY9FT/OO6DzpspoZ+TybLnEt6XAq2GE7a/G9x2KeGtjYpK9yemnI9UmT66LJOLX9GWU+p+q7jAqfRW80yylvqwkNOaVW5j83ZEpQrmSoMuqs0Owldc7Wt8vj7iKFPZcKu5pQyAkFEl3m8W94+ygMDTnluLdHbFwkmscaz1hjmXJ8RiTExgUBLjmx8ciMplvU+OJgg2NRl8vjDovBiN24zsXeHK0wpuElXB50uG9pi7RQLETjWQGoFIZp7pJpSd2zpjatMGa732ChMcaRGt+1RjaHOdpHGnbsL9THxLnDfG1CWigCldNs2gLoOHeZKM9GrJ2Ua8MWnpOT5k6Zu52ghGZ72KBRi+3nUkt2xzW7wpU7zIWTmbznYjBiWlgxhIM4ZHHjgGnmEDlW7nOlPuTLr/Ja943OJjaA6+Xt68Bh+O/fA/8rgBDCAe4F/jPQB6ZCiJUyTeRbgT8on/MH2Cj4x8rJ+l9U6SEVrxf/6Hvv5txGm/maz69+9MLNbk5FxW1L5GTMR2OkMCwGI5QwPNufZ73en7nDrUc9DpyIy4MO660+k8yj5qScau2RaUWqFZ4sbHGjH5Nrxbnla6TaoZeEBCrjwflNRrlHPwk43tynl9rl4FxLzi1eI9GKK6MOG/UDApVRd2xx44n5LqlWLIVDtJE0/ZipctFGsBCMiXOXce6xHAy5MJyn5U1Z9CccpPZ9W15MqDKeHixypraDK3Lu8raIjTuzpT50ZrzryBZtNea0b9PS4sBlWAQsu30CkbHmHszSQSbaZ9EZIp0+ShhOr28z1j73164BcKTdxT2chKGtYkg5YT50cTycbB4yLEJSo6hJ2/fCSArjMdYegczoFTXraldEdJwxB3mNa0mbpmMdNDvumFERsJU0+ezWUX7g+F9wkEU40k7+7qtv8uHte1mOBrTdKU89t8oDp68Sla6B08Ll3NxVlt0BZyN7LOD5NJmaSGfpMgB/s/05XFEQLBZIDBoxc3RUwpQpLFYNJRACF4EUAm0MxQ3Oj+qG7QAZV7mYe3xk+ADf1jlPW425v3aNr03WGGYBb3roCoM84G1rFwlVxoqa0JCCwpiZTvdJt0scKRoiJ0NYq/i2pKdD9os6X5ke4Xvmv8pHe2e5t76JNpJ+HpIZxW5c55nBIve1rzPOfRZ8O8lzRcGlyRxvn3tm9mOhm9fZy2yB/oI/4rMHx3h8sMabWlcIZEZdxXjlMbNFpnp22x4njdR2WyCy2fEGaKgphSMJRDYrmrWpQPbxY+0zp8a4IueEvwvAJ4tTNIMEKQxHoh6OKJjzJiSFQ8M9INeKT14/Tiea0vRjPJkzznySwuFkY5/1Wp9r4xauLCi0ZD+u2TQTVeBITcNJ8JR9zWnh2jQuI2lHU5ajoXU1LRybNiIMDy5ssp/UCJyMzVGLTEtWawOGo5AHN67iq5y2PyVyUiIn4/Kwg8SwFA3xZEGoMj556QQPH7nKcmRTujSC3Eg6wZQjUe9VX+u+0Qn2+4F/JoT4MnYS/d8YYwzwGSHEnwkhfhGrIvI/G2N6AEKI9wH/uxDiEtZ99TfK1/oV4INCiJ8FTgM//g22raLiVRO4ir9xbp1PPLN3s5tSUVFRUVFRcYvzDU2wjTH/Dvh3L7PvX7zM9i/xEpNnY8wUK99XUVFRUXGbIjC0/Wm5/G8jiC0/5kjU45nhIqu1Ab7MbTTJzRgkAUnusBCOCFXGgjfiqeEy/SSk5U9pOAkXhvMshwN2pg2Gqc9GzUbStJHc1dmh7qSEKuM6Lfan0czZ0C5fu9ScFEcUtF2rHZ1pxSAN6cYR7WDK8UbXFkbKgrPtbVLtcGE4T8ef4EjNfhIRFy73NLd4YrDC8XqXljeloWKupPOly142W57XyJk29SGBTFFGz9ItDiO3EVaKr60mALOCv0NqMmGs/VmEEqxjYUBGbCSpsAVusfHwRE5qHJsGIBO6eZ2drEHLmbKbNqiphHHhsxPXubuxzcXJPKtBn7pK+Ez/JADLvnXA86WNxnecMS015ZEzl2irMc0othKBDRsZfezE07YQE/h77/zYzJ3SLTW3XQGeEC+QNDt0Y3SFRJZ7EpMjy2ixi0IJG0G+kYnJZs/1hTOLLhcYNC/hdCvse/lIzro5k9p5ruVW/zkQGZfVPMMsoONM0EaQGUWuFQWCrULNijsDYVBQantDgEFJDWiWzYDMHTCvRsTG5fvnP49GctbdmY3/eE6RGRvtPjx/mXHYz+s8VLtMTab0ioix9smMokByZdKh4cashgOOhfs8PVniVLTLM9OlWfrGkwdL+Kqg6ccsB0Omhctq0LfHp5RLzIxi2R1QV3ZVAqCtJrNz1pTxTPoxNWq2ImLPT8HR8IBeGrEzrpMUDmcauzw1WGY5HBDJlK+M1jja6uGpnEnu0fJiPFWQFoqak/Cl62vcM7/D9UmTlcaQzUGT+9pb7KU14tzlchLx5rlLXI1tWmfNSdiNbTGlIzQ5ksVgxOVRh8VwxII/4uq4zda4wUptSD8N8FTBW088hxTWkXMlGLAVNwlVRtOPaXpT4sKl7U2ttvfSHqPMJmTM+WPa7pQvd9c5mIScbuz+l+PoZaicHCsqbkDeYMtbUVFRUVFRUfFXoaroqqi4gbecmOPvf+dpfvSx4ze7KRUVtyWFkcS5S8NJ2Jo2OFHb52Rjn7pKeGzuAltpkyf6KywGI9ZrfXppSK4lLTeml4b0sPeP1g9ItKKfBVzd7RA6GW3fynE1nSlf7q1zprnLKPfYS2o4QuOIgk4w5aneEgvhmOONfbSRuNJGfw+jwG13yiR3idyUk/U9Os6ExwdrLAUjairhetxiORwSFw4b4QFf6G7wQGeTphOzEIz46OVTvHX9EnPOiDcFl/n09CRfHR9hwR0SyZTP9E9wrnGVC9NF1vwef3z9Xn706KfoFxH9wkYx6ypmUvhEyhYFRjLFFQXX0zYawX5ax5cZ8+6Yifa4Frc5E+3wZ7t38djChZlzYahSBnnARnCAxBDIjOtpi1Wvz4I7ZNnt44qc+8KrL3D/KxC4zYKmSHCFhhazvGd7rDQuBnVDTCISwror8nwUusDMcp2fD2AoAuEQm9zmQyPRaDKjKXg+X7owBa6wzx8azfNp1AUSZjHpoty+WUSlLKCiJlIo+6GNIjbBLCp7WPR3WMzZkDFnXTjrDhjogIvpApFMWHCHKKHZz6z7Y5YrFr0hF7I5fmf/UdruhI4z4Yi3jy57Me+McCnKKLh1UAyE5n5vSGYMsbHtbsjDSLsEDNrkZAxm/SqMIfNtFDQQgtgYNBAbwZeSNR6MrjCvRgQiIxAZ39ewZjGZkcTzDgUSb8mO59i4MxfPsbGmQjt5E7ArIA05ZStvE8iMWLs8Ea8RyZRrSRtf5kQqZVJ4dNMa1yYt2r41L2o4CWtBj61Rg7lwwsXRHG13Qt1N2E9q5UpUzkow5I+evJcfuO9L7KV1TkZ79PKIukp4dPkKi96IZX9AL4u4v71Jx53gy4ztpMmRqMdu2iAuXFpuzLRwOVo7YJgFyHIFYJx7dIJJeW4Fp5p7jHKPtjtl6Acz5869tMaSPyTXikEaMMp89qcRx2td5rxJmc9tnTLjwqHjTTkSHrCbNjjT2iVvSj63++qV66oJdkXFDUgp+MC7z97sZlRUVFRUVFTcwlQT7IqKioqK1w2DYN4fI4VmMRjx7GgRjWCxPWTBHXIpnuOe1hbj3Oeu2jY7aYNBHnIs3Gczac9UIxa9IftZjWV/yLGzXTKjmJZmF70sYjkckhT2Ky5QGU0nYdEbMip8rnstciNZ8/tEKuGzveOca14lMQ5Xph0yrYicjDNlvuWCaxUGAFrOlKeyZY5GB1wYzSOFIXQypoXLxdEGZxo7/ODpLzEpPCu5JnPeGl7gQf/KTEHkzaFVKnosepoCwbefeWJmK35oHqONnP0vEKUKScF9/tWZukNWGrkA0LTyeW+vPzWT5DvM474x3zsQOXHk3KA4Ys13XA6VJZ7PVdaAL6wawSEZNmJ8qNTx4jzow2g1AjKjXxC1BWvVnhlJIBJ2i5BA5EihZ3btdr9DrF3SUuYQ4Jl4BVfmJNrl/HiJy8M5VmoDNsIDfJnTzWo0nBhXFMw5Y/68f5xvaV1kO2vy1f4qj81d4CCPaDlTtpIWoUrxZc6Xeke4p7nFe1p/wZozJDMOT05XWfcPeGayxIo/YFT4/MmVszy4dJ1eFrKf1ag5CYl2+POD47jzOZPC5uw+myzz8d1T3NPaxpcZjtSsej3eW/8KkSij0wgu5h5DHbCiRkgM3g3H/VAJRfL8sQ+EIDP2XK07B7iiwEPjiwKNIBA2qp8JQZt09lo21306u52ZKbEZctLdIzaKhrC1EKdc6w0RG8XQD+zYqR2eM4lCv8AcKRAZGYqvxev83ROfpJvX+UJ/AykMC/6IrbjJut+j6cQ0VMz7Hvxz+nmIIzR+ae5zLJhSYKUSQ5VRENNxJxTGGr0cDbv87rMP8o6jz3JXfYeLk3mujVs02wl316/z3HSRUKYsekOeGS/STSNO1Xb540v38NDyJr7M8b0RUhgS7XAQRzzYuMZW2uS+1nW6aY31qIcUmlWvz7WkzSj1aftTFgNb8+GKgppKqHsJrihoOLF1UXwVVBPsioqKiorXDU/mOLKg6Vi96PsXNukX4axwb94dUyDZCLosOkM6zpiP7N3LsdCmKKz5PdruBCU0ocpY9fq4ouBjB6dZCQYsh7aY69HWJYZFwHba5MGandyej1fKwqwu20mT3bTBRpBxrnkVV+b0s5Alf4QUmiVviMTw3HSB+8KrHI/2WfIGuKLgTH2HqfZoe1O0Eby5c4lEO0wLlzfXL7CZdWjKM5ZLAAAS1klEQVSpKWPtczGvMy+n5UTSTj7dcjIVyNTKuRlJJHNcDFmpOV286L8EJkbZNA+hiY0E8Xyh6OHrAKTi+fIqbSQZNv2lQOAKTVzOgTOjyGCWeiGFJqOYFbuNjUuBlW2baL/c5lEYOUsnyYxDahRDHeKK3OpLI3Ap6BZ1xtqnW9TYyxo8HF1iN2/yxGQVT+bcG21yPW2zmbRY8/t8fO8UJxt7TAuXRW9kj7EzYTtpcnnc4b72dc6E29xV2+FoeMC0cPnY1inetfYUx4J9Os647LPgZLRHJBOOeAfctbzF72y9iQfam7TUlNh12U3rHAu6fNfCU0Qy4Td3H+Oump0UL7gjGjJmIzigrmJ20wbfvfEUS96Qifb45N5JTjb22AgO6LgTMu0QyKz8wQPvXHqKifZY9XpcTuZRGP6f/qPcFVynm9fpFxEfuvYAb1t6jkilxNol0Q6rXp/CSHayBkf97kyuMZDp7HiuOH0uZ3McdbtcLBrMqxH7RZ22tJ+J3bxJQ5UpHDLGo5idew9NXBYoBiJnM+9w0t0j0XZcFGVaTyCyWToNgDLG/gCUNv2mrSazMXFvcK0svnQ4FnU5Fezwtckap2u7LLt9FpyhTejJ4YujDbZGDZbXBzhCcz1t4YqCdf+Afh7ZCbHMiGRKZhRH/X3ecuQSa36fRDucqe2w4I/ItaKlphwL9rkUz7Pu94ia6cyx8p1Hz7PuH5Bol7qKOT9ZYVq4hE5mXUqNY4tznSmTwisLPfs8OV7hbUvP0csiFr0RkUw5yKPys5rhy4xeFr7qa11V5FhRUVFRUVFRUVHxGlJFsCsqKioqXjeU0OwnNe6pXefCdBFZys4d5NEsbeEwXWIz7dByJqyFfT66e4aWN+VstEViHH73uQe5b3GLdf8AF6g5KSvegNwo1vwe/SKkn4e0nYlNkSijT3WVMCp8pDD4MmMvq3Mm3OZivEAgM746XuXbF84TyZTraZtQPb/cPimsTFrTiXG0JpQpkUpZ9XrsZQ3ONa6ijSxl8FJqMuFDvYf5juYTbGVta/KBnhXELTnD2bJ7Q04pjESXEeOx8V4o4ycynk5XWHQGzMsxW0VrZh7jUjAxPr3CRtti7RLIjMJIhjrgYrzA3eF1YuOy5h7Qzeu4oqBb2ByAJ0er1JwEbSSno20S7bLgDPmdrTfxrsUnZ46Se1ljllKx7h+gsMcwM4qaTHgmXiYzalaQ+aXBETrehLPRNsvugLH2+cLwKKt+n1PBDlfTOS5O5zke7nOQRzy2cAFf5FxNOny1v8oD7U1cWcyi1wpNIDKGRUCuJdtJk3etPYUSmkimM4OVno6QwhAbl72swRGvy1vmLhKpBFfk7KZ15t0xDRXz5dER7qtf483N5/jM4CRnoh02kzYdZ2wj/EYRypQvdDf41sULTAuX+WCMKsdPPw3xnZyJ9lhyB/TziAV3yKgI2MsaDPMAPFhwhpyPVznIIubdMfd0tm06hTOim9cY5z6FkRzx9ukXIQvOgN/eepSjtS7TwmPRG3JXuMVHR3fz7GSBt7SeQ6H5cPcB65JYuDTdmEfqFxlrn728wap7wCcGZzgbbVMguBLPUVcJvsw54e8QG49Yu/SKiLaaMC5XKW50vwxEykT7RDJhqEO0kcw5trjyy9MN7gk22S/q7OV16k4yS+mZc8ZsZy3qKmYna/IXvSMAfM/6kwQyo+1OeHa0wJvaVwhERsPrsp21CETOTmYLMEdFwKlol2ERMC1cojKtp+NM+Ez/JHfVtpEYImkLgQsEnz84SlI43L16nYaM7Zj3e+xldSQGhaauYhSGSNrVgy9317k7vM6Sb500j4X7s3SuRDv40rqb9vOIQVpFsCsqKioqKioqKipuClUEu6KiouIORwjxLuAHgB3AGGP+yYv2B8AHgWvAGeCXjDHny33vAx4GCuBZY8yvvtJ7ORR8z8LX+MOdB/ixtU/wdGKjnudql3FFwXbWYlgELDgDukWdRLucDHd5U/0SV9M5WmpMgeCf3PchvjZdJ9MOy16ftzQv2OiTv0esXYY64JHoOZ5JVlhzD2bR3Y47Yckb0s1rPBxdokBSkwmJ59JSY6L5lDW3x7AIuCu4Xhq0FDwYXaFXRPSLiJaaEMkEJQy7eYNraYe7gi3Oxyv4MmMnbfD25nm0kaVBiUO/iMrIWWldLQs+Mz7FnDMmNg5n/etcyeZZcfo8na3QL0I6zphAZLgiZ6J9ApkxLEL28zpPTtc46u8jhUEbgRSGg7zGMW+PnokIyGwUG8mbahfJjC1s/OzoJOdqlylKs50T/g6jMCDTilWvT2wcjnhdnpiu8UOrn7OmMdhiyAV3yPtWP82FZKnM7RYsqx6ZcfhPvbv51tbTtNWEa1mHfh7x7vmvcj5e4Yi3z9V0ngLJt7efYjtr2WMgCh5qXGHD7TLW3sxQZ84ZsegNWXV7RDLhriNbdPM6kUxoqCmBzJgYjwca11hwhrTVhCvZHGvOAV+JNygQHPG6zDkjMqN4errMvdGmjfaLgkVvxKrXY16NuKu2RUPGFEjurm1xxOvOpAh9kbPm9lh0hqz7PVtAGY54oHaVWLtIYZgon2P+Hrt5A4Wm5UxYcgaAlVpcdvs0lDWuWXMP2HQ6bGctzjUuA7CTNVlwRrScCYvOkN3c5qq7ouDh9hWOeF0up/O01JS2mrAtM94999VZ1Pkd7fNEMuFPe/dyX+0aNZmwlbc44e9wNZ0n14pj3h6fHJ7m7c3zbGYd5tRoFtmeVyOuZ+1ZfcBE25zkTDssu31roy4T2mrCJwZneKRxCVfkPJMs80j0HJ8eneZc7dKsH7F26bhWuvBSusBEe7TUdNaXifZpqTGZayPDS+4AhWbD3ed8vMLZ4DpSaP5s/yw/tPxZnolXeDCyUe5PDk/zUM0et4aK2cvqvL15nmeSZU7720ih+cEVG4XezRvMqRFZ4XB/eJUdt4kqV3wOP0eRTGj5E06s7VKTCQ9GVxgWAZlxWHQGpEbRcawMZqJdAP7Wyuf40Ku8rlYT7IqKioo7GCFEBPyfwH3GmEQI8TtCiHcaY/70hof9JHDZGPPPhRAPAL8OvEMIcQT4APCwMcYIIT4rhPiPxpinX/79oK3GPNS2usvLTp9AWFfAQGTMlV/SNZmimZAaB4WmrSY8UawRG4+5Uv+35UxItGtTLsTzahaHhXl2cloQyJQ2cDbapq5scaUUGin0LA3Dl7ZgcNU9IDOKoQ5oqwmemM5er6HismBMzpwZFYa7gi0ackqsXebViCVvaPeJoiyW1PgyIxDpTGu4IafMOWNbkFaE1GRCP4845e3QUmN8maGNQAmrrZxlDlfTOe4Pr1JoSYGkrSYMdEhbTWyb3JTYuDw+PMK75x7HEwVxOTFoqCkKQ71MkwiEYcEZArDuHeCV5yDWLq7I6WURUWSLGOsqnqUKSKGZc6wyQ78IZwolb24+Z49r6US55lmliwXXHotlt1++dsExb88qUciMhowJZMpQB7P0AoBVtzc7p4dpIRueVbpoqSktNWVYBEy0z3p5zoBZOos9dwWLzpCGjO3EqjzXy+5gdnvRGc7SAQ5/AC04Q3t+Hfucwgha5TG2x+6Gdno9XJGz6AwZFsFsn1c+7lAJZr+oc9zdJZIJc86YtpqUP5w8FssJuSx/AEQyITbubDJ4+EOjKJVlajJhM2vjipC2GqMwPFi/Sk0mSKEZFQGeVzDnWH1pJTQddzJrc01aZ1PrMJrSccbMq9GsyNETNiXi8PWaMkMJzYo/oCmnzyvcIFn17CR8wRnNVGsWnNHs2Hbzelm4aNNHAml/MCpjWC4n15lRaCQtNUWV/Xusc4GaTPiNJ97CLz78uwQyZd3vzT53sYrt51fasTH7LEtKt9AMzfN657UyjeTw8+BLW6RblAW9sky1GgufTKvy9fQsZUs5mmERvuDcfz2qFJGKioqKO5u3AZeMMUl5/xPAe170mPeAVacyxjwOPCSEaALvBj5vzEyr7VPA933zm1xRUVHxxkaYF2lY3moIIXaBS3+Fpy4Ae69xc95I3O79g9u/j1X/bn1eTR+PGWMWX4/GvBRCiB8BftgY81+V9/8e8B3GmPfd8Jinysd8qbx/FfgO4G8By8aYnyy3/wKAMeZnX/Qe7wfeX969H/jKN7NPb1DuhPH+UlT9vrO4E/r9qq7Zt3yKyF/1i0kI8TljzKOvdXveKNzu/YPbv49V/259bpE+7gCNG+43y22v5jE7wOkXbX/mxW9gjPk14NfgljkmrzlVv+8sqn5XVCkiFRUVFXc2nwKOCSH88v63An8ghJgr00AA/gCbSkKZg/0XxpgB8GHgESGEKB/3NuCPXr+mV1RUVLwxueUj2BUVFRUVf3WMMRMhxH8P/Osy5e7Lxpg/FUL8c6AL/BLwK8AHhRA/i41Y/3j53KtCiA8C/0oIUQD/1ysVOFZUVFTcKdzJE+xfu9kN+CZzu/cPbv8+Vv279bkl+miM+RPgT1607R/ecHsK/MTLPPe3gN/6S7zdLXFMvglU/b6zqPp9h3PLFzlWVFRUVFRUVFRUvJGocrArKioqKioqKioqXkOqCXZFRUVFRUVFRUXFa8gdl4P99SyB32gIIVaAXwAeMsa8udz2l7YtFkIcB34OK6F1HPhfjDEjIYQEfhEYAceAXzfGfPp16tupsm9fAI4A+8aYfyqEmMMWVl0o+/czxpjt8jn/ACsF1gE+Yoz5/XL7OWyO6HPAEvABY0z+SsfqdeqjBD4EfAbwgFPA3wXC26WPZdtCbB8/Yoz5wO0yRst2fRqIy7uFMeadt9MYfb241a69L8edMh5u5nfPzRwrL9PvHwP+O54/779ujPnNct/t0u+b+n38csfxlsYYc8f8ARF2sPvl/d8B3nmz2/V12vyDwHuBz92w7aeBf1jefgD4WHn7CPAlns+t/yxwprz9x8C3lLf/R+B/K2//beD/KG/PAecB9Tr17c3A37jh/teAR7C2zT9Ubnsv8Jvl7bcAf1jedoGngTYgsMYVK+W+fwn8+Csdq9fx/EngZ2+4/3vAf3079fGG9vwG8MHbaYyW7/nzL7Httjp/r8MxvOWuvXf6eOAmfffc7LHyMv3+MeD4Szz2dur3Tfs+fqXjeCv/3WkpIq/GEvgNhTHm/wWGL9r8l7ItFkK4wHdiBy28sN83vlYX+wv9vm9Ob16IMeazxpjfu2GTBMY3tulFbf3rN7Q1A54Avg04CYTGmK2XeM7LHavXBWOMNsb8AoAQwsFeSJ7iNuqjEOLvlO157obNt8UYLXlACPGPhBA/L4T4L9rELX7+XiduuWvvK3BHjIeb+N1zU8fKy/Qb4O8LIT4ghPjHZVQXbq9+38zv45c8jq9pB28Cd1qKyBIv/OAMym23Gi/Xj5fbvgBMbxi8N/b7DXFMhBDfD3zYGPOkEOLGNg2ATjk5XcJ+iLlh3xKwy8v34eX6N3jNO/EKCCHeDfwU8O+NMZ+7XfoohLgXuMcY8zNCiAdv2HU7jdFfNsb8uRBCAf9ZCDF8UZtu2fP3OnKzz+FryZ08Hl6Pz/Xiy2y/mXwU+ANjzK4Q4q8Bvw28k9u03zfh+/h2uj7MuNMi2K/GEvhW4JVsi19q+x4Q3uC2dmO/b/oxEUJ8J/bX/k+9RJuawIExJucv3+8Xv9aL971uGGM+bIz5XuCEEOJ/4Pbp4/cDsRDip4G3A98ihPjJV2jTLTdGjTF/Xv4vgI9hx+rtcv5eL26bPv7/7d2xi9RAGIbx5wNPFCuvEgsLQdBDK22srhIES3sbwU6Fq6wsBD3FRgux8J8QEewUxErEzsbmsLK4XkGLz2IGLjl2BSWb7CbPD7bYwO7Ol5kks5u8m4mPhz6266WrPzN3MnO3Pn0LbNYvWKOre6Dj8VLU3rWpTbBn3hJ4wPb8r3+6bXE9ffOOco0VtOtuvtc6cAj40kcR9TOvUE4P3QaORcTFZpv2tfV1o60HgA3gPSV88bOGU/a/Zt666kVEbDROI0O5jOIkI6kxM+9n5r3MfAh8AD5m5pO/tGmlxmhEnI6I641FpyjXSY6i/3o0in2v46GX7XrpxkpEbNf+g9LnO/UL1qjqHvB4PHM9LqLGPk3uRjMRcYkSYtgFfueSJ9kjYhO4BlwGnlMCA1CSuN8pty1+kO0k7gVKEvdrthPNdymD/wSwlXuJ5m3gR13+Ivv7F5HzlFNvn+qiI8Az4BXwCPhG+deNO9lOLR+tjzfZTi3frK9ZZy+1fJg566oPNZn9mJLMXgPOALeAX2OpsbbtKiU1fpDShy/ntWnFxujxWs9nyq8qa8AWJcwzmv7rw6rte2eZ0ngY8tgz5FiZU/cN4CzlB5JzwNNGW8dS96DH43nrcZVNboItSZIkLdLULhGRJEmSFsoJtiRJktQhJ9iSJElSh5xgS5IkSR1ygi1JkiR1yAm2JEmS1CEn2JIkSVKH/gBjm4zsxzBXggAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 864x288 with 2 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "from scipy.io import wavfile\n",
- "from matplotlib import pyplot as plt\n",
- "## mono audio file # 49152 samples\n",
- "rate, x = wavfile.read('sounds/test_000.wav')\n",
- "\n",
- "b=x[:].copy()\n",
- "\n",
- "## Create al subplots at once\n",
- "fig, (ax1,ax2) = plt.subplots(1,2,figsize=(12,4))\n",
- "\n",
- "ax1.set_title('Raw audio signal')\n",
- "ax1.plot(b[:])\n",
- "ax2.specgram(b[:], Fs = 0.2)\n",
- "ax2.set_title('Spectrogram')\n",
- "\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Extension - Other plots as packages\n",
- "\n",
- "- Graphs\n",
- "- Sankey diagrams\n",
- "\n",
- "### Additional packages: \n",
- "- networkx\n",
- "- jgraph\n",
- "- pySankey"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "### Graphs"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 19,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFCCAYAAADL3BUJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3Xd0VOXexfFvKiT0JiAIKkKoCaGDIggivQjSJ9KRkoACghQFFUVpigQQUIozSJOi0rtIEelNIKBUaYKUEBJS5rx/5Mrr1QukTHJmMvuzVtZdF5KTPWqy5znnPL/jYRiGgYiIiDgNT7MDiIiIyH9TOYuIiDgZlbOIiIiTUTmLiIg4GZWziIiIk1E5i4iIOBmVs4iIiJNROYuIiDgZlbOIiIiTUTmLiIg4GZWziIiIk1E5i4iIOBmVs4iIiJNROYuIiDgZlbOIiIiTUTmLiIg4GW+zA4jj2Q04fg2u3038/3n8ISAPeOmtmIiIS1A5ZyDX78IX++GTn+BOLHj/p4zj7ZDFF96oCt0rQF5/c3OKiMjDeRiGYZgdQlJv/E54exN4eEB0/P/+HD9vMAwYVRsG10j8XBERcT4q5wxg4Dr4fC/cjUva5/v7QPdgmNQgbXOJiEjK6Cqki5u8K3nFDImf+9fpbxERcT5aObuwu3Hw2HiISkYx/52fN1wdBFl9HZtLRERSRytnF7bgSOquG3t6wNeHHZdHREQcQ+XsogwDPt6eeFd2SkXFwcc7Eo8lIiLOQ+Xsom7dg9M3U3+cC7fhz+jUH0dERBxH5eyibkSDr1fqj+PrpXIWEXE2GkLiohw17SsqKooO7bpQNIed/PnzP/AjS5YsjvmGIiLySLpb20VFxULOsYnTv1LD28Pg2xrbuXP9IleuXHngh5eX10PL++8f2bJlw0MTTkREUkzl7MKenw0/nk/dMaoXhh1dH/45hmEQGRn50PL++0dCQkKSizxnzpwqchGRf1A5u7AVEdBhKUSm8I7tbL5gfRmaBzg2V1RUVJKLPDo6msceeyxJRZ4nTx48PXWbhIhkfCpnF5Zgh8cnwtW7Kfv6PH5weeD/PyDDDDExMVy5coWrV68+sshv375N3rx5k1Tk+fLlw8vLAXfMiYiYQOXs4jadhibzH/ywiwfx84Zv20K9YmmTKy3Exsbyxx9/JGlFfuPGDXLlypWkIn/sscfw8fEx++WJiNyncs4AFh6FLt8mvaD9vOGLptChXNrmMlN8fDzXrl1LUpFfu3aN7NmzJ7nIM2fObPbLE5EMTuWcQWw5Y9Bw+iUM/3zEGj7881+qB4nPdM7rB7OawQtPmZHSOdntdq5fv56kIr969Sr+/v73i/pRZa4taCKSEirnDOK7775j6LBhTF1xkIk/ebH2V4hNSJy97eMJ9Z5OfIbzc0X0HOfUMAyDGzdu/KuwtQVNRBxJ5ZwBxMfHU65cOSZMmECjRo3u/3lsQuL/OmKSmCSftqCJSEqpnDOA6dOns2jRIjZs2KBf2C4sOVvQYmJikrwFLXfu3NqC5kB2A9aeSnwm+vnbiW+Cc2WGBs9At2DI6292QskIVM4uLjIykoCAAFasWEGFChXMjiPp5K8taEn5iIyMJF++fP+6sU1b0JInNgE+/Qkm/pT4RLd/PhHOzxsMoElxeK82lMpnQkjJMFTOLm7kyJH8+uuv2Gw2s6OIk4qNjf2v6+IPu0auLWj/260YeMkGh68+eleEp0diUS9tAy+50FZFcS4qZxd28eJFypUrx759+yhatKjZcSQDSKstaPnz5ydTpkxmv7wUiYmHGrPg6B//fx9HUvj7wJoOUFM/mpICKmcX1qNHD3LlysXYsWPNjiJuKKVb0JLy4e/vPBdu+61OvL6c3EE/ADkywe9vJG5jFEkOlbOLOnr0KC+88AIRERHkzJnT7DgiD/W/tqA97MPHx+eRp9TTYwtaVCw8NgHuxqXs67P4wMSXoGdFx+aSjE/l7KIaN25MvXr1eP31182OIuJQhmFw+/btB67A//lndrs9yXeuJ3cL2oy9MGBd4g1gKVUsF5wM1XwBSR6VswvatGkTPXr04NixY/j66nyZuLe03IIWON2To3+kLl8WH/ixMwQXdMSrFXehcnYxdrudSpUq8dZbb9GmTRuz44i4lOjo6CQ9Ae3KlSvcuXOH+Df/wMiUI1XfM3sm+KqF4x/NKhmbt9kBJHm+/vprfH19ad26tdlRRFyOn58fRYsWTdLuhtjYWHKM8yEmGXdo/y92I/HatUhyqJxdSExMDMOHD2fevHmaBCaSxnx9ffH3hZjo1B3H0yNx9SySHJrp50ImT55MhQoVeO6558yOIuIWyjhgyldsApTWtDBJJq2cXcT169cZO3Ys27ZtMzuKiNt4szocuAyRqTgtXbEgPJ3LcZnEPWjl7CJGjx5N69atCQjQXSUi6aVRcciUilHj/l4JDKnhuDziPlTOLuDXX3/FarUycuRIs6OIuBUvTxhZK3E7VHJ5Yifm+jn2L/qA+PgUjBcTt6ZydgHDhg3j9ddfJ3/+/GZHEXE7fStD69KJs7KTytMDcvl5srNnZn7cuoWaNWty8uTJtAspGY7K2cnt2rWL7du3M2DAALOjiLglDw/4slnis5ozeyaA/eF7q7L4QOFssKcHVClZkLVr19KhQwdq1KjBtGnT0GgJSQoNIXFihmHw/PPP06VLF7p27Wp2HBG3ZhgGQc364lVzCMfjiuLh8f8Pw/D2gEzekM8fBj8LIYGQ9R/D+44fP47FYiFfvnx8+eWXPP744+n/IsRl6G5tJ/btt99y69YtOnXqZHYUEbf3/fffY5z5kT3LJ3MtGpYeh0uRiQWd1x9qFIbnijx4hnbJkiXZuXMno0ePJjg4mPDwcA0TkgfSytlJxcXFUbZsWSZNmkSDBg3MjiPi1uLj4wkMDGTcuHE0btw41cf7+eefCQkJoXLlyoSHh+vJcvIvuubspL744guKFClC/fr1zY4i4vbmzp1Lvnz5aNSokUOOV6VKFfbv30/OnDkJDAxk48aNDjmuZBxaOTuhyMhISpQowapVqwgODjY7johbu3v3LiVKlGDJkiVUrVrV4cdft24dXbt2pVWrVnz00Uf4+fk5/HuI69HK2QmNHTuWevXqqZhFnMCkSZOoXr16mhQzwEsvvcShQ4e4evUqFSpUYM+ePWnyfcS1aOXsZH7//XcCAwPZv38/RYoUMTuOiFu7du3a/Ru5ihcvnubfb/78+fTv35+wsDCGDh2Kt7fu2XVXKmcn061bN/Lly8dHH31kdhQRt/fGG28QGxvLlClT0u17Xrhwga5du3L79m2++uorSpQokW7fW5yHytmJHD58mBdffJGIiAhy5EjdA95FJHVOnz5NpUqV+OWXX9J9Op/dbmfq1KmMGjWK9957j969e+sxsW5G5exEGjZsSMOGDenXr5/ZUUTcnsVi4ZlnnmHUqFGmZThx4gQhISHkzp2bWbNmaXCJG9ENYU5iw4YNnDp1il69epkdRcTt7d+/n40bNzJw4EBTcwQEBLB9+3aqV69OcHAwCxcuNDWPpB+tnJ2A3W6nYsWKDB8+nFdeecXsOCJu76WXXqJFixb06dPH7Cj37d69m5CQECpUqMCUKVPIlUsPic7ItHJ2AjabjcyZM9OqVSuzo4i4vfXr13PmzBl69OhhdpT/UrlyZfbt20eePHkICgpiw4YNZkeSNKSVs8mio6MJCAhg/vz5PPvss2bHEXFrdrudSpUqMWzYMKc+i7V+/Xq6du3Kyy+/zEcffYS/v7/ZkcTBtHI22WeffUalSpVUzCJOYP78+fj6+jr9Wax69epx6NAhrl27RoUKFdi9e7fZkcTBtHI20V8DDnbs2KG9jCImu3fvHiVLlmTOnDnUqlXL7DhJtmDBAvr160ffvn0ZNmwYPj4+ZkcSB1A5m6h///4kJCQQHh5udhQRt/fpp5+yYcMGVqxYYXaUZPv999/p2rUrN27cwGq1EhAQYHYkSSWVs0lOnTpFtWrVOHbsGPny5TM7johbu3XrFiVKlGDjxo2ULVvW7DgpYhgGU6dOZeTIkbz77rv06dNHg0tcmMrZJK1btyY4OJhhw4aZHUXE7Q0bNozLly8za9Yss6Ok2l+DS3LlysWsWbMoVKiQ2ZEkBVTOJti5cydt2rThxIkTustSxGR/PWzm4MGDFC5c2Ow4DhEXF8eHH37IlClT+Oyzz2jXrp3ZkSSZVM7pzDAMnnvuOXr06EHnzp3NjiPi9rp3707evHkz5MNm/hpcEhwczJQpU8idO7fZkSSJtJUqnS1btow7d+4QEhJidhQRt/fLL7/w3Xff8dZbb5kdJU38NbgkX758BAUFsW7dOrMjSRJp5ZyO4uLiKFOmDJMnT6Z+/fpmxxFxe82bN+f55583fYZ2evhrcEnz5s0ZO3asLqk5Oa2c09H06dN58sknVcwiTmDbtm0cPHiQvn37mh0lXfw1uOTGjRsEBwdrcImT08o5ndy+fZsSJUqwdu1agoKCzI4j4tYMw6BGjRr06dPHLS8xLVy4kH79+tG7d2+GDx+uwSVOSCvndPLxxx/ToEEDFbOIE1i2bBnR0dF07NjR7CimaNu2Lfv27eOnn36iRo0aHD9+3OxI8g9aOaeDCxcuEBQUlKG2aoi4qri4OMqWLctnn33m9peYDMNg2rRpvPPOO4waNYo+ffrg6ak1mzNQOaeDLl26ULBgQT788EOzo4i4vc8//5xvvvmG9evXa4LWf0RERBASEkKOHDmYPXu2Bpc4AZVzGjt48CD169fnxIkT5MiRw+w4Im7tzp07lChRgu+//56KFSuaHcepxMfHM2bMGCZPnsykSZNo37692ZHcmso5jdWvX5+mTZsSGhpqdhQRt/f+++/zyy+/MH/+fLOjOK09e/YQEhJCUFAQU6dO1eASk+jiQhpat24dp0+f5rXXXjM7iojbu3r1KpMmTeKDDz4wO4pTq1SpEvv27SN//vwEBgaydu1asyO5Ja2c00hCQgIVKlTgnXfecfoHt4u4g7CwMDw9PZk0aZLZUVzGhg0b6Nq1K82aNdPgknSmlXMasVqtZM2alZYtW5odRcTtnTp1ivnz5zNixAizo7iUF198kUOHDnHz5k2Cg4P5+eefzY7kNrRyTgN3794lICCAhQsXUqNGDbPjiLi9tm3bEhgYyPDhw82O4rIWL15MaGgovXr1YsSIERpcksZUzmlgzJgx7N27l2+++cbsKCJub/fu3bRo0YKIiAiyZMlidhyXdvHiRbp168a1a9ewWq2ULFnS7EgZlsrZwf744w9KlSrFzp07KV68uNlxRNyaYRjUqVOH9u3b07NnT7PjZAiGYTB9+nRGjBjBO++8Q2hoqAaXpAGVs4OFhYXh4eHBZ599ZnYUEbe3evVqBgwYwOHDh/H29jY7ToZy8uRJQkJCyJYtG7Nnz9b0QwfT2x0HioiIYP78+bzzzjtmRxFxewkJCQwZMoQxY8aomNNA8eLF2bZtG7Vq1aJChQp8/fXXaK3nOFo5O1CrVq2oXLlyhn1wu4grmTt3LjNmzGDbtm0a05nG9u7dS0hICOXKlWPatGkaXOIAWjk7yPbt29m9ezf9+/c3O4qI24uJieHtt99m3LhxKuZ0ULFiRfbu3cvjjz9OYGAga9asMTuSy9PK2QEMw+DZZ5+lV69evPrqq2bHEXF748aNY8eOHSxbtszsKG5n06ZNdOnShcaNGzNu3DjdIZ9CWjk7wJIlS7h7967bPhtWxJncuHGDsWPH6ilwJqlTpw4HDx4kMjKS4OBgdu3aZXYkl6SVcyrFxsZSunRppk2bRr169cyOI+L2Bg8ezM2bN5kxY4bZUdzeN998Q9++fXnttdd4++23NbgkGVTOqfTZZ5+xatUqXWMRcQLnzp0jODiYw4cP8/jjj5sdR4BLly7RrVs3rl69itVqpVSpUmZHcgkq51S4desWJUqUYP369QQGBpodR8Ttde7cmcKFCzN69Gizo8jfGIbBjBkzGDFiBCNGjLj/EBJ5MJVzKgwdOpQrV64wa9Yss6OIuL1Dhw5Rr149Tp48Sfbs2c2OI//DqVOnePXVV/H392f27Nk88cQTZkdyWnrrkkLnz59nxowZvP/++2ZHERHgrbfeYvjw4SpmJ/bMM8+wdetW6tSpQ8WKFbHZbBpc8gBaOadQp06deOKJJ3T6TMQJbN68mW7dunHs2DEyZcpkdhxJgn379hESEkKZMmWYNm0aefLkMTuSU9HKOQUOHDjAunXrGDx4sNlRRNyeYRgMGTKEDz74QMXsQipUqMCePXsoXLgwgYGBrF692uxITkXlnEyGYfDmm2/y9ttv6/SZiBNYvHgxdrudtm3bmh1FksnPz4+JEyditVrp1asXvXv3JioqyuxYTkHlnExr167l3Llz9OjRw+woIm4vNjaWYcOG8fHHH+vuXxf21+CSqKgoypcvz08//WR2JNPpv+ZkSEhI4M033+Sjjz7SZnoRJzBjxgyeeeYZ6tata3YUSaWcOXPy1Vdf8dFHH9G8eXNGjBhBbGys2bFMoxvC/uHgZZhzEM7chOh4yOsHLzwF7crAQtssZs2axY8//qhh+iImu337NiVKlGDt2rUEBQWZHUcc6NKlS3Tv3p3Lly9jtVopXbq02ZHSncoZMAxYcBTGbINf/4R7CZDwt38qWX3BbjfgoBVbr3K8/EKweWFF3IjdgJPX4Xo0eHpAHj94Jjd4eMDIkSP57bffsFqtZseUNGAYBjNnzmTYsGGMGDGCfv36udWlC7cv59gE6LAU1pyCqLiHf66HPZ6smb1Z1QGeK5I++UTc0fW78OV+mPgT3IkF7//8To6zJxb0a2VvMz4kkP07t/Dkk0+amlXS1l+DS/z8/Jg9ezZFirjHL1+3Lme7Ac0XwMbTiaewk8rfBza/ClUKpV02EXdkGPDxdnh3K3jw4J9Lb/s98PBgcmNfelVK14higvj4eMaOHcsnn3zCxIkTsVgsGf7SoluX80fb4f2tcPcRK+b/JVdmOPd64ilvEUk9w4Cw1TD7YNJ/Jv19YFB1eLd2mkYTJ7F//34sFgulSpXi888/J2/evGZHSjPucwL/H+LtMG5HyooZEk+Hzzvs2Ewi7mz8zuQVMyR+7vidMHt/2uUS5xEcHMzevXspWrQoQUFBrFq1yuxIacZtV87LjkOn5RCZijv1n84Jp8ISb04RkZS7FQMFJkJMMi4v/V32THB1IGTydmwucV5btmyhc+fONGjQgPHjx5M1a1azIzmU266cP/kpdcUMcCUK9lx0TB4Rd/bVocS7sVPKbsDS447LI86vdu3aHDx4kJiYGMqXL8/OnTvNjuRQblvOp/5M/TE8PeDUjdQfR8SdGUbqLjFB4h3dH293XCZxDTly5GDOnDmMHTuWl19+meHDh2eYwSVuexIoOhW/CP6SYEDkvdQfR8SdXYyEP+6m/jhHrib+XPtpeJ/badmyJTVq1KB79+5Uq1YNq9VKmTJlHvo19oQETm/axM0zZ4iLiiJT9uw8Vq4cj1eq5BR3grttOfv7wM1UFquXR+K1LhFJuRsx4OsJMak8jq9X4rFUzu6pQIECfP/993zxxRfUqlWLYcOG8frrr/9rcEnU1avsnTGDnyZNIuHePYyEBOwJCXh6J9Zhtscf59khQyjXvj0+/v5mvBTAjW8Iq/sVbDqTumNk8YEfO0NwQQcEEnFTv/wB1b5M/T0gmb3hTD/In7HuC5IU+PXXX3n11Vfx9fVlzpw5FC1aFICIlSv5pm1bjIQE4mMe/HbQN2tWfPz96bR5M/lMGh3qttec36gG2VK5R9kn+gp+t3QXikhq5PNPHJmbWnEJkMsv9ccR11esWDG2bt1K/fr1qVSpEl999RVHFy9mcevWxEVFPbSYAWLv3CHqjz/4olo1rhw2Z8+s266cE+yJWzeupfBal7+3nToxy9k9ow/lypUjNDSUJk2a4OXl5digIm6g/HQ4eCV1x6j7FGwIcUweyTgOHDhAaKtW1D17Fs+E5L8L9M+bl9CICPxy5UqDdA/mtitnL08Y/lziteeU8PfxZOHbLTl79iydOnVizJgxFCtWjLFjx3L9+nXHhhXJ4IY8m7ozWVl9YXANx+WRjKN8+fL0KlkSjxQUM0BsVBT7vvjCwakezW3LGaB/VWhSPPkFndUn8R26vw9kypQJi8XCTz/9xOLFizl69CjPPPMM3bp1Y/9+jS0SSYqWJVM3zCebL7z4tOPySMZx5/JlzmzcSEr/84qPjmbnxIkYdrtDcz2KW5ezhwfMawmtSyfe3PUovl6QMzNs7gRBBf7995UrV2bu3LlERERQrFgxmjVrxrPPPsuCBQsyzN47kbSQyRusLcAvBftH/LxhfsvUDTGRjGvvjBmp3hoVd+cOv65f76BESePW5QyJj6Kb3Szxh7tG4cQ7Pn3+8U8lmy/kyARvVIVfekOlxx9+zHz58jFs2DBOnz7NwIEDmTFjBk8++STvvvsuly5dSrsXI+LCmgXApAbJK2g/b/iqBdR6Ms1iiYs7s2XLI28Ae5S4u3e5uGePgxIljdvuc/47Dw9oGpD4cepPsB2CM7cSBxrk84eaReHlkokr5+Tw9vamZcuWtGzZkiNHjjBlyhRKly5NgwYNCAsLo3r16k6x2V3EWfSoAIWyQcu5f2L4ZiWWf1+I9iDxklJe/8Rifr5o+ucU1xFzI/VjHA27nbvXrjkgTdKpnP/hmdwwqrbjj1u2bFmmTZvGmDFjmDNnDp06dSJbtmyEhobSvn17/Py0B0QEINe1neSd25bP151k0h7YcjZxxCckDv6p/wy8WR2eK6KHzsijeTvod6tvOj9Yw223UpnNbrezdu1awsPD+fnnn+natSu9e/fmySefNDuaiGkMw6BWrVp07tyZrl27/ufPIDo+8ZpyZi0nJJmWdOzIkfnz//8dXgr4+Pvz0sSJVHrtNQcmezi3v+ZsFk9PTxo2bMjKlSvZuXMncXFxVKxYkRYtWrBhwwb0nknc0apVq7h27Rqvvvrq/T/z8Eg8ja1iluRISEhg06ZNbLhxg9hU/j417HZKv/KKg5IljcrZCTzzzDNMnDiRc+fO0ahRI9544w1Kly7NlClTiIyMNDueSLpISEhg6NChjBkzBm9vNbGkzOHDhxkyZAhFixZl4MCBPFO3LrkLFUrx8Tw8PQlo1gz/PHkcmPLRVM5OJEuWLPTs2ZNDhw7x+eefs2XLFooWLUq/fv04ceKE2fFE0tS8efPIli0bzZo1MzuKuJjff/+d8ePHExQUROPGjfH09GTNmjXs37+fgQMH8vywYSl+iIV35sxUHzTIwYkfTdecndz58+eZPn06M2fOJCgoiLCwMBo1aqQxoZKhxMTEULJkSaxWKzVr1jQ7jriAyMhIli5ditVqZd++fbRs2RKLxcLzzz//rydR2RMSmN+kSbK3VflkyUKNN9+k9siRjo7/SCpnF3Hv3j0WLVpEeHg4V69epU+fPnTr1o3cuXObHU0k1T755BM2bdrE999/b3YUcWJxcXGsW7cOm83GqlWrqF27NhaLhSZNmjxyx0tcdDQLmjfn/PbtxN199EMVfPz9qdy3Ly9+/LEpW15Vzi7o559/Jjw8nO+//55WrVoRFhZGUFCQ2bFEUuTWrVuUKFGCjRs3UrZsWbPjiJMxDIPdu3djs9lYuHAhxYoVw2Kx0KZNG/LmzZusY9kTEtgxdiw7JkwgITaW2H/c0+Ph6Ym3nx9ZCxSg7ocfUqZNG0e+lGRRObuwq1evMnPmTKZNm8ZTTz1FaGgoLVu2xMdHT5sX1zFixAguXLjAnDlzzI4iTuS3335j3rx52Gw27HY7ISEhdOzYkWLFiqX62Pb4eE6uWsWuSZO4cfo08dHR+GbNSoHgYKoPGEChqlVNHxClcs4A4uPj+fbbb5k8eTInT57ktddeo2fPnhQo8D8GgIs4kUuXLlG2bFn2799PkSJFzI4jJrt+/TqLFy/GZrMRERFB27ZtsVgsVKlSxfSyTG8q5wzm8OHDTJkyhYULF9KoUSNCQ0OpVq2a2/2HLa6hd+/e+Pv7M2HCBLOjiEliYmJYuXIlVquVzZs307BhQywWC/Xr13frs4Aq5wzqxo0bzJkzhylTppAjRw7CwsJo27atxoSK0zh58iTVq1fnxIkT5EnnPaRiLrvdzrZt27BarSxZsoTg4GAsFgutWrUie/bsZsdzCirnDM5ut7NmzRrCw8PZs2fP/TGhRYvqaQFirrZt2xIUFMSwYcPMjiLp5JdffsFmszFv3jyyZ89OSEgIHTp0oHDhwmZHczoqZzdy8uRJpk6dyldffcXzzz9PWFgYL7zwgk55S7rbs2cPzZo14+TJk2TJksXsOJKGLl26xIIFC7DZbFy+fJmOHTtisVgIDAw0O5pTUzm7oTt37mCz2QgPD8dutxMaGsqrr75K1nR+6oq4J8MwePHFF2nTpg2vpeODBCT93Llzh+XLl2O1Wvn5559p0aIFFouF2rVra4BSEqmc3ZhhGPzwww9MnjyZzZs3ExISQt++fSlRooTZ0SQDW7duHaGhoRw9etStb/jJaOLj49m4cSNWq5UVK1bw3HPPYbFYaNasGf4pHJ3pzlTOAsC5c+eYPn06X3zxBcHBwYSGhtKwYUO9yxWHstvtVKpUiWHDhvFKOj/lRxzPMAz279+P1WplwYIFFClSBIvFQtu2bXnsscfMjufSVM7yX2JiYli0aBGTJ0/mzz//pE+fPnTt2pVcuXKZHU0ygPnz5/PJJ5+wa9cu3evgws6ePXt/QEhMTAwWi4WOHTsSEBBgdrQMQ+UsD7Rr1y7Cw8NZsWIFrVu3JjQ0VDdxSIrFxsZSqlQpvvjiC1544QWz40gy3bhxg2+++QabzcbRo0dp3bo1ISEhVK9eXW+00oDKWR7pypUrzJw5k88//5ynn36asLAwWrRooeuFkix/vdFbs2aN2VEkie7du8fq1aux2WysX7+eevXqERISQsOGDfH19TU7XoamcpYki4uLY/ny5YSHh/Prr7/eHxOaP39+s6OJk7tz5w7Fixdn1apVBAcHmx1HHsIwDHbs2IHNZmPx4sWUKVOGkJAQXnnlFXLmzGnMdxnMAAAgAElEQVR2PLehcpYUOXToEOHh4SxevJjGjRsTGhpKVScYFi/O6b333uPEiRPMmzfP7CjyAH/9+7HZbGTOnPn+gBANLDKHyllS5caNG8yePZspU6aQO3duQkNDadu2LZkzZzY7mjiJq1evUqpUKXbv3s3TTz9tdhz5m6tXr94fEHL+/Hnat29PSEgI5cuX1xttk6mcxSESEhLujwndt28f3bp1o1evXnrSkNC/f38Mw+Czzz4zO4oAd+/e5dtvv8Vms7F9+3aaNm1KSEgIderUwdvb2+x48h8qZ3G4iIgIpk6ditVqpXbt2oSGhlK7dm29E3dDv/32G5UrV+bYsWPa92qihIQENm/ejM1m49tvv6Vq1aqEhITQvHlzTQZ0UipnSTORkZH3x4R6eHgQGhqKxWLRLwM3YrFYKF68OCNHjjQ7itsxDINDhw5hs9n4+uuvKViwIBaLhXbt2ulZ7y5A5SxpzjAMNm/eTHh4OD/88MP9MaHFixc3O5qkoQMHDtCgQQNOnjxJtmzZzI7jNi5cuHD/xq7bt2/fHxBSunRps6NJMqicJV2dO3eOadOm8eWXX1KxYkXCwsJo0KABnp6eZkcTB2vYsOH9O/klbd26dYslS5Zgs9k4ePAgrVq1wmKx8Nxzz+lny0WpnMUUMTExLFy4kMmTJ3Pz5k369OlDly5dNCY0g9i8eTPdu3fn2LFjGlaRRuLi4lizZg02m401a9ZQp04dLBYLjRs31m6JDEDlLKYyDOP+mNCVK1fSpk0bQkNDKVeunNnRJIUMw6BatWr079+fDh06mB0nQ/nr58Vms7Fw4UICAgIICQmhdevW5M6d2+x44kC6b15M5eHhQbVq1ahWrRqXL19m5syZNGjQgOLFixMaGkrz5s01JtTFLF26lNjYWNq1a2d2lAzj1KlT968je3p6EhISwq5du7RvPAPTylmcTlxcHMuWLSM8PJzTp0/Tq1cvevTooa04LiA+Pp4yZcrw2WefUb9+fbPjuLRr166xaNEirFYrv/32G+3atcNisVCpUiVtS3QDKmdxagcOHGDKlCl88803NGnShLCwMKpUqWJ2LHmAGTNmsHDhQjZs2KACSYHo6GhWrFiB1Wpl69atNGrUCIvFQr169XQGyc2onMUl/Pnnn8yaNYupU6eSN29ewsLCaNOmDZkyZTI7mvzH3bt3KV68OMuXL6dy5cpmx3EZdrudrVu3YrVaWbZsGRUrVsRisfDyyy+TPXt2s+OJSVTO4lISEhJYvXo1kydP5sCBA3Tv3p1evXrxxBNPmB3N7Y0ZM4b9+/ezaNEis6O4hCNHjmCz2Zg3bx558uTBYrHQvn17ChUqZHY0cQIqZ3FZJ06cYOrUqdhsNl544QVCQ0OpVauWTqea4Pr16wQEBLBjxw5KlChhdhyndfHiRebPn4/NZuPatWt07NiRjh07aneC/IvKWVxeZGQkVquV8PBwvLy87o8JzZIli9nR3MagQYOIiopi2rRpZkdxOpGRkSxbtgyr1cqePXto2bIlFouFWrVqaUCIPJDKWTIMwzDYtGkT4eHhbN26lU6dOtGnTx+eeeYZs6NlaOfOnSM4OJgjR45QsGBBs+M4hfj4eNavX4/VamXVqlU8//zzWCwWmjZtip+fn9nxxAWonCVDOnPmDJ9//jmzZs2icuXKhIaGUr9+fa1U0kCXLl14/PHH+eCDD8yOYirDMNizZw82m40FCxbw9NNPY7FYaNu2LXnz5jU7nrgYlbNkaNHR0SxYsIDJkycTGRlJ37596dy5Mzlz5jQ7WoZw5MgR6tSpw8mTJ8mRI4fZcUxx+vTp+wNC4uPjsVgsWCwWnbGRVFE5i1swDIOffvqJyZMns3r1atq2bUtoaChly5Y1O5pLa9asGbVr12bAgAFmR0lXf/75J4sXL8Zms3H8+HHatGlDSEgIVatW1Q2J4hAqZ3E7ly5dYubMmUyfPp0SJUrcHxPq7a1ptsmxbds2OnbsyIkTJ9ziQQv37t1j5cqV2Gw2Nm7cSIMGDbBYLNSvX18P9xCHUzmL24qNjWXZsmVMnjyZs2fP0rt3b3r06EG+fPnMjub0DMPgueeeo2fPnnTq1MnsOGnGbrezfft2rFYrS5YsISgoCIvFQqtWrdz2NL6kD5WzCLB//36mTJnCkiVLaNasGaGhoZpy9RDfffcdw4cP58CBA3h5eZkdx+GOHz+O1Wpl3rx5ZM2alZCQEDp06KBhN5JuVM4if3P9+vX7Y0Lz589PaGgorVu31pjQv0lISCAwMJCPP/6YJk2amB3HYa5cuXJ/QMjFixfp0KEDFouFoKAgXUeWdKdyFvkfEhISWLlyJeHh4Rw6dIgePXrw2muvUbhwYbOjmW727NnMmjWLrVu3unxpRUVFsXz5cmw2Gzt37qR58+ZYLBbq1KmTIc8IiOtQOYs8wvHjx++PCa1bty5hYWHUrFnT5YspJaKjowkICGDBggXUqFHD7DgpkpCQwMaNG7HZbHz33XfUqFGDkJAQmjVrpqly4jRUziJJdPv27ftjQn18fAgNDaVjx45u9Qt9/PjxbNu2jeXLl5sdJVkMw+DAgQPYbDbmz59PoUKFCAkJoW3btuTPn9/seCL/onIWSSbDMNi4cSPh4eFs27bt/pjQYsWKmR0tTd28eZMSJUqwZcsWSpcubXacJDl37tz9ASF3797FYrHQsWNHSpYsaXY0kYdSOYukwpkzZ5g2bRqzZs2iatWqhIaG8tJLL2XIMaFDhw7l6tWrfPnll2ZHeaibN2/yzTffYLPZOHz4MK1bt8ZisVCjRo0M+e9FMiaVs4gDREdHM3/+fCZPnkxUVNT9MaEZZS/s77//TmBgIAcOHHDK7USxsbGsXr0am83GunXrePHFFwkJCaFhw4a6015ckspZxIEMw2Dnzp1MnjyZtWvX0q5dO/r27UuZMmXMjpYqPXv2JGfOnIwdO9bsKPf99c/aZrOxaNEiSpcuTUhICK+88gq5cuUyO55IqqicRdLIpUuXmDFjBtOnT6dkyZKEhYXRtGlTlxsTevz4cWrWrMmJEyfInTu32XGIiIi4fx3Z19f3/oCQJ5980uxoIg6jchZJY7GxsSxdupTw8HDOnz9P79696d69u8s8RrBVq1ZUqVKFIUOGmJbhjz/+YOHChVitVs6ePUv79u2xWCxUqFDBLbe0ScanchZJR/v27WPKlCksXbqU5s2bExYWRsWKFc2O9UC7du2iVatWRERE4O/vn67f++7du3z33XfYbDa2bdtGkyZNsFgsvPjiiy539kEkuVTOIia4fv06X375JVOnTqVgwYL3x4Q609ONDMPghRdewGKx0L1793T5ngkJCWzZsgWbzcby5cupUqUKFouFl19+maxZs6ZLBhFnoHIWMVFCQgIrVqwgPDycI0eO3B8TWqhQIbOjsXr1agYMGMDhw4fTfKV66NAhbDYbX3/9NY899hgWi4X27dtTsGDBNP2+Is5K5SziJI4dO8aUKVP4+uuvqVevHqGhoTz33HOmXFO12+0EBwczatQoXn755TT5HhcuXLj/oIkbN27QsWNHLBaLy9/ZLuIIKmcRJ3P79m2++uorwsPDyZw5M6GhoXTo0CFdr/nabDamTJnCjh07HPrm4Pbt2yxduhSr1cr+/ftp1aoVFouFmjVrakCIyN+onEWclN1uvz8mdMeOHXTu3JnevXvz9NNPp+n3vXfvHiVLlmTOnDnUqlUr1ceLi4tj7dq12Gw2Vq9eff86dpMmTcicObMDEotkPCpnERdw+vRppk2bxuzZs6lWrRphYWG8+OKLKVptxtth5Un49Cf47SZEx0EWXwh8DAZUg/3LJ7F+/TpWrlyZ4ryGYfDzzz9js9lYuHAhxYsXx2Kx0KZNG/LkyZPi44q4C5WziAu5e/fu/TGh0dHR9O3bl06dOiVpTGiCHcbthPE7IDYBImP/++89AH8fg+jrF3i3tsGIJkWSne/XX3+9PyAEuP+giYz+UBARR1M5i7ggwzDYvn074eHhrFu3jvbt29O3b98HPi0qJh5eXghbz8HduEcf398HugTB5IbwqEvO169fZ9GiRVitVk6dOkW7du2wWCxUrlxZA0JEUkjlLOLiLl68yPTp05kxYwZlypQhNDSUpk2b4uXlBYDdgOYLYONpiI5P+nH9fSC0Mnz84r//LiYmhhUrVmC1WtmyZQuNGjXCYrHw0ksv4ePj46BXJuK+VM4iGURsbCxLlixh8uTJXLx4kd69e9OtWzeWn8tL/7VJWzH/k78PrOkANYsm3qD2448/YrVaWbp0KRUqVMBisdCyZUuyZ8/u+Bck4sZUziIZ0N69ewkPD2fZ8uXYQ48T6ZM/RcfxAGoVjKTabx8yb948cuXKdX9ASOHChR0bWkTuUzmLZGBrjtyk+VJ/YknFWND4GHrfG0uvji0IDAx0XDgReSBNjxfJwBb/lpMUnM3+L5kzZyKg8Tuol0XSj0byiGRgv92A1J4ai4n34Nwth8QRkSRSOYtkYDHJuDv7Ye7EPvpzRMRxVM4iGVhuP8cc57EsjjmOiCSNylkkA6v9JPil8s6SbL5Q5XGHxBGRJFI5i2RgXcuDPZUbMjJ5QaPiDgokIkmichbJoAzDYNv6b/H5bQ3YE1J0DC97LL2C7+Gl3xQi6Uo/ciIZ0L59+6hTpw7Dhw9nfONs+GfySsFRDLyMe1j7PcsPP/zg8Iwi8mAqZ5EM5MKFC3Tq1InGjRvTrl07Dhw4wGstn2Nhq+Rde/YAsvp6sKt3NiZ/PJIOHTrQv39/oqKi0iy7iPw/lbNIBnDnzh3efvttgoKCKFy4MCdOnOC1117D2zuxkZuUgO/aQVbfR5d0Vl/I6w87ukD5AtC0aVMOHz7Mn3/+Sfny5dm2bVs6vCIR96bxnSIuLCEhgdmzZ/POO+9Qt25dPvjgA4oUefBzmK/fhVkHYOJOiIpLfGJVvB18vMAwoGA2eOtZaFcGsvyPiZ/Lly+nT58+tGvXjtGjR+Pv75+Gr07EfamcRVzUunXrGDRoELly5WLChAlUqlQpyV9rN2DrWTh9E6JiIXsmKJUXKj3+6Oc3X7t2jbCwMPbt28ecOXOoXr16Kl+JiPyTylnExRw9epRBgwZx6tQpxo0bR/PmzfF4VKOmgSVLlhAaGorFYuG9997Dz89BE09ERNecRVzFlStXeO2113jhhRdo0KABR48epUWLFqYUM0CrVq04dOgQZ8+epUKFCuzatcuUHCIZkcpZxMlFR0fzwQcfUKZMGbJmzcqJEyfo378/vr6peAykg+TLl49Fixbx7rvv0rx5c4YOHcq9e/fMjiXi8lTOIk7KbrdjtVoJCAjgwIED7Nq1iwkTJpArVy6zo/1LmzZtOHjwICdOnKBChQrs3r3b7EgiLk3XnEWc0A8//MDAgQPx8vJi4sSJPPvss2ZHShLDMFiwYAGvv/46PXr04O233yZTpkxmxxJxOSpnESdy8uRJBg8ezP79+xkzZgxt27bF09P1TnBdvnyZXr168euvvzJ37lwqVKhgdiQRl+J6P/UiGdD169fp378/1atXp1q1ahw/fpz27du7ZDEDFChQgGXLljFkyBAaNGjAyJEjiY3VQ6FFkso1f/JFMoh79+4xceJESpYsSXx8PMeOHWPIkCFkzpzZ7Gip5uHhgcVi4cCBA+zbt48qVapw8OBBs2OJuASVs4gJDMPgm2++oXTp0mzevJmtW7cyZcoU8uXLZ3Y0h3v88cf57rvveOONN6hXrx7vvfcecXFxZscScWq65iySznbt2sXAgQO5c+cOEyZMoG7dumZHSje///47PXr04PLly8ydO5dy5cqZHUnEKWnlLJJOzpw5Q/v27WnVqhXdunVj7969blXMAIUKFWLlypWEhoZSp04dPvjgA+Lj482OJeJ0VM4iaezWrVsMGTKEihUrUrJkSU6cOEGXLl3w8krJM5Zdn4eHB127dmXfvn1s3bqV6tWrc/ToUbNjiTgVlbNIGomLi2PKlCkEBARw7do1Dh8+zMiRI8mSJYvZ0ZzCE088wZo1a+jZsye1a9fmo48+0ipa5D90zVnEwQzDYOXKlbz55psUKlSI8ePHU758ebNjObWzZ8/SrVs3IiMjmTNnDqVKlTI7koipVM4iDnTgwAEGDhzIpUuXGDduHI0aNTLtwRSuxjAMpk+fzttvv83gwYMZMGCA2576F1E5izjA77//zogRI1i9ejUjR46kR48eeHt7mx3LJZ0+fZquXbty7949Zs+eTUBAgNmRRNKdrjmLpEJUVBSjRo0iMDCQAgUKcOLECXr37q1iToWnnnqKjRs30qFDB5599lk++eQTEhISzI4lkq5UziIpkJCQwKxZsyhRogQnT55k3759jBkzhhw5cpgdLUPw9PQkNDSUXbt2sWzZMmrVqsXJkyfNjiWSblTOIsm0YcMGKlSowKxZs1i2bBnz5s2jaNGiZsfKkIoVK8aWLVto06YN1atXZ9KkSdjtdrNjiaQ5XXMWSaJffvmFN998kxMnTvDxxx/TsmVL3eyVjk6ePHl/f/isWbMoVqyY2ZFE0oxWziKPcPXqVXr37k2tWrV48cUX+eWXX2jVqpWKOZ0VL16cH374gebNm1O1alWmTJmiVbRkWCpnkQeIjo5mzJgxlC5dmkyZMnH8+HHeeOMNfH19zY7mtry8vBgwYADbt2/HZrNRt25dTp8+bXYsEYdTOYv8g91u5+uvv6ZkyZLs3r2bnTt38umnn5InTx6zo8l/BAQEsG3bNho1akTlypX5/PPP0RU6yUh0zVnkb7Zt28aAAQMwDIMJEybw/PPPmx1JHuHYsWN06tSJHDly8MUXX+jmPMkQtHIWAU6dOkWrVq3o2LEj/fv3Z9euXSpmF1GqVCl27NhB3bp1qVSpEjNnztQqWlyeVs7i1v7880/ef/99rFYrAwcO5PXXX8fPz8/sWJJCR44coXPnzuTNm5eZM2fyxBNPmB1JJEW0cha3FBsby6effkrJkiWJiYnh6NGjDB06VMXs4sqWLcvOnTupWbPm/b3oWn+IK9LKWdyKYRgsW7aMIUOGULx4ccaNG0eZMmXMjiVp4NChQ3Tq1ImCBQsyc+ZMChUqZHYkkSTTylncxu7du6lVqxajRo1i6tSprFq1SsWcgQUGBvLzzz9TrVo1goODmTt3rlbR4jK0cpYM79y5cwwdOpTNmzfz/vvv07lzZz2K0M0cOHCATp06UaRIEaZPn87jjz9udiSRh9LKWTKs27dvM3ToUIKDgylWrBgRERF069ZNxeyGypcvz+7duwkODiY4OJh58+ZpFS1OTStnyXDi4+P54osvePfdd6lfvz6jR4+mcOHCZscSJ7F37146d+5MsWLF+PzzzylQoIDZkUT+RStnyTAMw2DVqlUEBQWxaNEiVq1axZw5c1TM8l8qVqzInj17KFOmDEFBQcyfP1+raHE6WjlLhnDw4EEGDRrE+fPnGTduHE2aNNGDKeSRdu/eTefOnSlZsiTTpk3jscceMzuSCKCVs7i4ixcv0q1bN1566SVatGjB4cOHadq0qYpZkqRy5crs3buX4sWLExgYyOLFi82OJAKonMVFRUVF8e6771KuXDny5s1LREQEffv2xcfHx+xo4mIyZ87MRx99xLfffsvbb79NmzZt+OOPP8yOJW5O5SwuxW63M2fOHAICAjh27Bh79uzh448/JkeOHGZHExdXtWpV9u/fT9GiRQkMDGTp0qVmRxI3pmvO4jI2bdrEwIED8fPzY+LEiVSrVs3sSJJB7dixgy5dulCxYkUmT56sx4VKutPKWZze8ePHadq0Kd27d2fYsGFs375dxSxpqkaNGuzfv58CBQpQrlw5vv32W7MjiZvRylmc1h9//MGoUaNYtGgRQ4YMISwsjEyZMpkdS9zMjz/+SJcuXahevTqTJk0id+7cZkcSN6CVszidmJgYxo4dS6lSpfDy8uLYsWMMGjRIxSymqFmzJgcPHiR37twEBgayYsUKsyOJG9DKWZyGYRgsXLiQoUOHEhQUxNixYylRooTZsUTu++GHH+jSpQvPP/88n376KTlz5jQ7kmRQWjmLU9ixYwfVq1dn3LhxzJ49m+XLl6uYxenUqlWLQ4cOkTVrVsqVK8fq1avNjiQZlFbOYqpff/2Vt956i127dvHBBx/QsWNHPD31nlGc36ZNm+jWrRt16tRh4sSJ2s4nDqXfgmKKGzduMHDgQKpUqUL58uU5fvw4ISEhKmZxGXXq1OHQoUP4+vpSrlw51q1bZ3YkyUD0m1DSVWxsLJMmTSIgIIDIyEiOHj3K8OHD8ff3NzuaSLJly5aNadOm8eWXX9KjRw969uzJ7du3zY4lGYDKWdKFYRgsX76csmXLsnr1ajZu3MiMGTP0uD7JEOrVq8fhw4cxDIPAwEA2bNhgdiRxcbrmLGlu7969DBw4kGvXrjF+/HgaNGhgdiSRNLN27Vp69OhBkyZNGDt2LFmzZjU7krggrZwlzZw/f55XX32VJk2a0KFDBw4cOKBilgyvfv36HDp0iJiYGAIDA9m8ebPZkcQFqZzF4SIjIxkxYgTly5enSJEiRERE0LNnT7y9vc2OJpIucubMyaxZswgPDyckJISwsDCioqLMjiUuROUsDhMfH8+MGTMoUaIE586d48CBA4wePZps2bKZHU3EFI0aNeLw4cPcvn2bwMBAtm7danYkcRG65iwOsWbNGgYNGkTevHmZMGECFStWNDuSiFP5/vvv6dWrF61bt+bDDz/UDgV5KK2cJVUOHz5M/fr16devHx988AGbN29WMYv8D02bNuXw4cNcu3aNoKAgtm3bZnYkcWIqZ0mRy5cv06NHD+rWrUvjxo05cuQIzZs3x8PDw+xoIk4rd+7c2Gw2xo0bR5s2bRg4cCDR0dFmxxInpHKWZLl79y6jR4+mTJky5MiRgxMnTtCvXz98fX3NjibiMlq0aMGhQ4e4ePEiwcHB7Ny50+xI4mRUzpIkdrudr776ioCAAA4dOsTu3bsZP348uXLlMjuaiEvKmzcv8+fPZ/To0bz88ssMHjyYmJgYs2OJk9ANYfJIW7ZsYeDAgfj4+DBhwgSeffZZsyOJZChXr16lb9++HDlyhLlz51KlShWzI4nJVM7yQBEREQwePJiDBw8yZswY2rZtq2vKImlo0aJF9OvXjy5dujBq1CgyZcpkdiQxiU5ry79cu3aNfv36UaNGDWrUqMGxY8do166dilkkjbVp04aDBw9y4sQJKlasyJ49e8yOJCZROct99+7dY/z48ZQqVQq73c6xY8cYPHgwmTNnNjuaiNvInz8/S5YsYdiwYTRu3JgRI0Zw7949s2NJOlM5C4ZhsGjRIkqVKsXWrVv58ccfCQ8PJ1++fGZHE3FLHh4e9+fRHz58mMqVK7Nv3z6zY0k60jVnN7dz5877ey0nTJhAnTp1zI4kIn9jGAbz5s1jwIAB9O7dm+HDh2vrohtQObugiIjr7Nx5nps3Y/D19aJgwWy89FIx/P19knyM06dP89Zbb7F9+3ZGjx5NSEgIXl5eaZhaRFLj4sWL9OzZkwsXLjB37lyCgoLMjiRpSOXsIuLj7Xz//Qk+/ng7Bw9ewcvLg/h4O56eHnh7e2K3G3TpUp5+/apSvHieBx7n5s2bfPjhh3z55Zf079+fgQMHkiVLlnR8JSKSUoZhMHfuXAYPHkxYWBhvvfUWPj5Jf1MurkPl7AKuXo2ibt2vOHPmJnfuxD7w83x8PPH29uS9915g0KAa//V3cXFxTJ8+nffff5+mTZvy/vvvU7BgwbSOLiJp4MKFC/To0YOrV68yZ84cypUrZ3YkcTCvUaNGjTI7hDzYtWt3qVBhBmfP3iQmJv6hn2u3G8TH29m+/TwxMXHUqfMUhmHw/fff07JlSy5duoTVaqVnz556jKOIC8uePTsdO3bE29ubkJAQ4uPjqV69Op6eusc3o9DK2YnZ7QYVK87g6NGrxMXZk/W1/v4+DB9ejvXrJ3LlyhXGjx9Pw4YNtVdZJIM5d+4c3bt358aNG8ydO5fSpUubHUkcQOXsxNav/5WWLRc99FT2w3h6RhIeXowePXrg7e3t4HQi4iwMw2DmzJkMHz6cQYMGMXDgwEf+zNuJ5Rp7iOEadmLxJis5CCAbT6VTankYlbMTq1fPyoYNv6X467Nk8WHFig7Urv2k40KJiNM6c+YM3bp1Iyoqijlz5lCyZMl/fc5dLnOOpZxnJQAGCRjY8cQLA4MsPMHTtCc/NfFEN5uZRRconNSFC7fZtu1cqo5x924c48Ztd1AiEXF2Tz75JOvXr6dTp07UrFmT8ePHk5CQcP/vz/M92+jEWZaRwF0SuIudexjEkUAMdu4RySmOMJ5tdCaGP0x8Ne5N5eyk9u+/hK9v6vYdGwbs2XPJQYlExBV4enrSu3dvfv75Z1auXEnNmjWJiIjgNIs4xhTsxGLw8JtLE4gmmivsoKcK2iQqZyd169Y97PbUX3FI6fVqEXFtTz31FBs3bqRDhw70evsljsVNx07SZ3QbJBBHJD/zBvZHlLk4nsrZSWXO7I2nZ+rvrM6USVO/RNyVp6cnoaGhjLA+i6dP8nZ8QGJB3+NPrqLLY+lN5eykChXKhiPu1XvsMU3/EnFnt4gg3vd6ir8+gWh+Y74DE0lSqJydVNWqhcmaNXXD7bNk8aFv38oOSiQirugM32AnLlXHuMNp7nDWQYkkKVTOTsrT04OBA6sn62EW/5SQYPDqqxqOL+LObnIESP4p7b/zwIvbRDgmkCSJytmJde0anOKvzZTJi3btypAjR2YHJhIRVxNPdKqPkXhz2B0HpJGkUjk7sVy5/Pj665b4+SVvupe3twdPPJGDSZMaplEyEXEVnqR+OqAHnniRyQFpJKlUzk6uefOSTJ/eNMkFnSmTF08/nZsff+xC9uz6YRJxd5nJ64CjeJLJIbJvPOQAAAHxSURBVMeRpFI5u4CQkEDWrQuhWrXC+Pl54+Pz739tWbP6kiWLDz16VGTv3p4UKJDVhKQi4myK8DJe+KXqGB54kocKDkokSaHZ2i4mIuI6kyb9xMaNp7l9+x6+vl4UKJCVXr0q0bZtGfz8NAtXRP5fArFsogUJKbz27IkPT9KWEnRzcDJ5GJWziEgGd5ypnONb7CR/YqAnvjyPjczkS4Nk8iA6rS0iksEVpxtZeAKPZN4c5kkmyjBAxWwClbOISAbnRSYqM5GsFMWTpA038iQTAfSmEPXTOJ38LzqtLSLiJhK4x0lmc57vSdy9/M/r0J544kMWilCS18hDRTNiCipnERG3YyeWy2zlHMuJ4Rp24vDGn1wE8iSvkI2nzI7o9lTOIiIiTkbXnEVERJyMyllERMTJqJxFREScjMpZRETEyaicRUREnIzKWURExMmonEVERJyMyllERMTJqJxFREScjMpZRETEyaicRUREnIzKWURExMmonEVERJyMyllERMTJqJxFREScjMpZRETEyaicRUREnIzKWURExMmonEVERJyMyllERMTJqJxFREScjMpZRETEyaicRUREnIzKWURExMmonEVERJyMyllERMTJqJxFREScjMpZRETEyaicRUREnIzKWURExMmonEVERJzM/wHP1OXBDQhUpwAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {},
- "output_type": "display_data"
- }
- ],
- "source": [
- "import networkx as nx\n",
- "import numpy as np\n",
- "import matplotlib.pyplot as plt\n",
- "\n",
- "G = nx.Graph()\n",
- "G.add_edges_from(\n",
- " [('A', 'B'), ('A', 'C'), ('D', 'B'), ('E', 'C'), ('E', 'F'),\n",
- " ('B', 'H'), ('B', 'G'), ('B', 'F'), ('C', 'G')])\n",
- "\n",
- "val_map = {'A': 1.0,\n",
- " 'D': 0.5714285714285714,\n",
- " 'H': 0.0}\n",
- "\n",
- "values = [val_map.get(node, 0.25) for node in G.nodes()]\n",
- "\n",
- "nx.draw(G, cmap = plt.get_cmap('jet'), node_color = values)\n",
- "\n",
- "plt.show()"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 20,
- "metadata": {
- "scrolled": true,
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- "<div id=\"graph-6bf9f6ac-3133-4263-b62f-320c8e3683ca\"></div>\n",
- " <script type=\"text/javascript\">\n",
- " require.config({baseUrl: '/',\n",
- " paths: {jgraph: ['nbextensions/jgraph.min', 'https://rawgit.com/patrickfuller/jgraph/master/js/build/jgraph.min']}});\n",
- " require(['jgraph'], function () {\n",
- " var $d = $('#graph-6bf9f6ac-3133-4263-b62f-320c8e3683ca');\n",
- " $d.width(600); $d.height(400);\n",
- " $d.jgraph = jQuery.extend({}, jgraph);\n",
- " $d.jgraph.create($d, {nodeSize: 2.000000,\n",
- " edgeSize: 0.250000,\n",
- " defaultNodeColor: '0x5bc0de',\n",
- " defaultEdgeColor: '0xaaaaaa',\n",
- " shader: 'basic',\n",
- " z: 100,\n",
- " runOptimization: true,\n",
- " directed: true,\n",
- " showSave: false});\n",
- " $d.jgraph.draw({\n",
- " \"edges\": [\n",
- " { \"source\": 1, \"target\": 2 },\n",
- " { \"source\": 2, \"target\": 3 },\n",
- " { \"source\": 3, \"target\": 1 },\n",
- " { \"source\": 3, \"target\": 4 },\n",
- " { \"source\": 4, \"target\": 1 }\n",
- " ],\n",
- " \"nodes\": {\n",
- " \"1\": { \"location\": [ -1.4833928299113084, -1.5475477261721466, -2.0 ] },\n",
- " \"2\": { \"location\": [ -0.36595077585773733, -0.5073725912000406, -0.5747580364199643 ] },\n",
- " \"3\": { \"location\": [ 0.4012116636705649, 0.5873752438894282, 0.7255818543075399 ] },\n",
- " \"4\": { \"location\": [ 1.4481319420984806, 1.4675450734827593, 1.8590633353289536 ] }\n",
- " }\n",
- "});\n",
- "\n",
- " $d.resizable({\n",
- " aspectRatio: 600 / 400,\n",
- " resize: function (evt, ui) {\n",
- " $d.jgraph.renderer.setSize(ui.size.width,\n",
- " ui.size.height);\n",
- " }\n",
- " });\n",
- " });\n",
- " </script>"
- ],
- "text/plain": [
- "<IPython.core.display.HTML object>"
- ]
- },
- "metadata": {},
- "output_type": "display_data"
- }
- ],
- "source": [
- "import jgraph\n",
- "#jgraph.draw([(1, 2), (2, 3), (3, 4), (4, 1), (4, 5), (5, 2)])\n",
- "jgraph.draw([(1, 2), (2, 3), (3,1), (3,4), (4,1)])\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## Sankey plots"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 245,
- "metadata": {},
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWQAAAD7CAYAAABdXO4CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3Xd0VMUewPHvpPdQQxCR0EIRAtKRYuhVBAIK8pBmAQQeKISgIAGlBUQUEfAhRRApAiIgSpFQIkWQXjS0CFKlpPfM+2OXGCCBJCTZ3eT3OSfn7G0zv3t389vZuffOVVprhBBCmJ6VqQMQQghhIAlZCCHMhCRkIYQwE5KQhRDCTEhCFkIIMyEJWQghzIQkZEApVUYptV4ptUsptV0pFayUejsHyv1AKXVNKRWYA2Fmts7ZSqm7Sqm+xmkHpdQlpZRTXsWQ1x63j0qpekqpI0qpi9ksf7VSKk4p5ZvJ9asqpfYrpfYqpbZmp05jOW8qpS4qpRZnt4ycpJR6VSm1wNRx5GeSkA0WAz9rrZtqrVsAgcDAJy1Uaz0R+OlJy8linUOBI2mm44DqWuuYvIwjLz24j0op37TJV2t9ABj+BOV3B65lYZMxwHqtdUNg7RPU+yWGz2YqY2Ohb3bLzIgx8fummfZSSj14k8JKnuA4iseThGxQDwi+N6G1Dga+MVUwOU1rfdfUMeQ2M9vHp4ErAFrruSaOJcdorZO11lGmjiM/k4RsEAb4K6Wc783QWk+999r40/FXpdQvxi6Nqsb5qT+FlVKjlFI7lVLHlFLe6VWilPpcKRVtbOU4KqVclFILlVJ7jOUPNK43QSmVqJQ6rJSqoJSqrpQ6pZQ6rZQqnk65dZRSB43lfAKoNMu+SftzWyn1rFJqszHWvUqpNx8o6z2l1Eml1Bal1GillDbG+4xSap9xuq/xWCQZW1KZPT4hSqkDxm3mGY/VkgyOVWOl1GWl1F9KqQHGecvTHKP3lVI3jOWm7qNSqhIwC/A0xr36gXIf+z4Z12tnXCdYKfVeOstfMx6Pnca43IzzvwCeAwKM27orpboopXYrpXYoQ7dYI+O6zZVSZ5RSwcbpLo/qolBKTQFqpim7QzrrVDa+D78Y6+ybZlkb43serJTaoJR6yjh/EeAJzDIuewFYYVwWbPyrodJ0+yilOhlj36mUmmY8FiFKKY90juFOpdRHxn07YvxcZBhngaa1LvB/QAvgFnAXWAS88MDytwB742tfYHeaZb5AAtDYOP0FMD/N8sUYukAUMBtok2bZ/4Cvja9dgfNpyvkBeC/Nup8B5dKJ3Q64BPQ0TtcE4oC+ada5CPgaX9cH6htf2wKngYrG6fbAVaCIcfpjw0cktRwvQAOvGaffBUpm8vg0ME5/DxwE3AF74Ma9Zens2+sYupLA0Hi4DmwwTtsASzPYR1/g4gNlPfJ9emDdYkAU8LxxuhOQmKb8RsA/QHHj9HRgQZrtgx84/v9Jc0y9gL/SLOsLBKeZDgQWP2L6vrLTiX0V8IrxtSew2fi6LBAJVDJOvw1sS+/4pX2v0zmGFx+IPRooa5z+ERjziGOYkuYYphtnQf+TFjKgtd4OPAOMxPBB3KGUmp9mlVPABqXUbmAqUPuBIqK01nuMr49h+PA/6AvgN631zwBKKSugN/CVMYZIYINxHsDX914rpWyBZ7TW59MptyHggeEDjtb6CPDnI3Y3FBiglAoBtmJIqM8Zl3UHftRa3zZOZ9Rts95Y18da66s8/vhEaq33GV+fAMK01uFa63hjrOUyqGcT0FQp5QI0AL4DmiulHICmwJ4MtstI2vfpKOm/TwAdgOta61+N+/kDEJtmeV8MXww3jdPLgV5KKUX6jgKLlFJ7MHxBl07bksxht4FuSikvrfU1wM84/1XgoNb6jzQxt1BKlXzC+v7QWl8wvk772U/vGKbt7sgozgJNErKR1jpaa71Aa90MaAa8rpQqr5RyBzYCX2qtmwA9AMcHNo9I8zoOQ6s1rQFAFaBrmnnFMbQQg+79LAReMM4DQ3IuoZSqh6HlmtHJwZLAXa11cpp5tzNYF2AmhgTeVGvti+EE4L2rE0piaPk9shytdfi915k8PpFpXielM/3g8bpXz71k3wrDMfgYQwveF8M//I/p72KG0r5P8RnVy8PHAe4/Fk9j+GK4977NxtB6L5pBeT9g+NXQ2HjM4d9jntNGYPgC+MX4BdAgTcxV08S8DkNXXYknrC+jz/7jjmFGcRZoNqYOwBwopeZqrQfdm9Za71RK3QLcMPyTufFvQrTNRhXfAh8BJ5RSPbTWK4CbGJLCEK31b8Y4bDH+o2qt45VSq4DXgCLAkAzKvgoUUkrZaK2TjPMySgxgOIH5RZoEnnZ/rmL4orjnUeXcU4knPz6PshHoCDhorc8rpTZhSM6eWutLOVzXPQ8eBzC8B/dcAs5rrVMvjVRKFdNaP5iAMLaEvTAeH+N7nFYC/34JAxTKftiG7bXWHymlJmHoKtlgjOEShhZyar+zUqow9yfUnPS4Y5hunFrr6FyKxyJIC9mgpbElCoDxpIYGzmBoRSRh6HsFaJuN8mO01hHAm8BspVRxrXUKaboljMZiSMD3fA30BFSaboQH7cXQD/uKMfaaGFrjGTmLcV+MP1d90ixbBbRXSt1LxC9nYt9y4vg8yiYMvywuG6c3YvgHDn3ENpEYv9iU4brs0tmo0yPNybeXAJc0yxcDHYwJDeOJxA0ZlHXv3ERGx+cCUFEpZW/simn2mNgiASelVEWl1PR0li9SSpXQhs7ZXRi+IDWGRkF9pVQZY8wewE7+zQH3ym2mlPqvcRqllJNSKkApldUW7IPHsBP3/3LKKM6CzdSd2ObwB7yB4cO5A8OHI5g0J5owXJN8EUMy+ATDB2cLUBXDT/44YD6G1ucZDP+AQcA7GK5fvYihD28Chr7IPzH85HYBFgC/GuufBVg/EFso0OUx8dcFDgEhwJcY+lbPYDiR8o0xviMY+nYrYzipthdYiKHf7wzQ3FjWexi6CX4ChmE8sYOhdbPPuO/BQNVsHJ9OxvWuAYOAD4zHKrX+dPZNGddvapy2w5AsGqZZ58F9tAF+Me7jauDZR71PGdTbHjhu/DxMNsZ9BKhnXP4f4/H4xXisvI3zv0izTx8b53XGcML2Z2CS8fjs498TfUsx9K0vw9D9cQ14H8MX+L3j9b5x3S7AH8ABoFk6cfcxfg5+Mb7Pr6RZ1tq4LNi4PO1nfIjxfd8HPJvmuB7CcK6heppjuBponuYYTnjgvX3ngWMYjOHa7DCMJ8wfFWdB/lPGgyPMlFLqJ6CT1johD+qyAZy0oTWPUqousFFr/aT9jKIAUkoV0Wl+2SmlooC6WuvTJgzLrEmXhRky/hxtqAzX857Li2Rs5IWhBXnPfzC06oTIju+N3TAopbpiOPH5qK6mAk9O6pkndwx9flcx9CHnlX8Ae6XUrxi6Ci4Bg/OwfpG/7AV2K6ViMXTT+Ol/TzyLdEiXhRBCmAnpshBCCDMhCVkIIcxElvqQixUrpr28vHIpFCGEyJ8OHTr0j9b6oYHBHpSlhOzl5cXBgwezH5UQQhRASqmwzKwnXRZCCGEmJCELIYSZkIQshBBmQhKyEEKYCUnIQghhJiQhCyGEmZCELIQQZkISshBCmAlJyEIIYSYkIQshhJmQhCyEEGZCErIQQpgJSchCCGEmJCELIYSZkIQshBBmQhKyEEKYCXnqtBBZcODAAfz9/UlISKB169YAxMXFERcXx549e9i/fz/W1taZLm/x4sV07tyZQoUK5VbIwoJIQhYiC+rVq4evry9RUVEEBgYChoS8bds2PvnkE5RSWSpv8eLF+Pr6SkIWgCRkIZ5IUlISAQEBNG/enLJlyxIcHMzVq1cZNGgQtWvXplChQixdupSTJ0/y7rvvUqVKFc6fP0+fPn2IiYnh4sWLzJo1i8qVKzNw4MAM65k3bx5Hjx6lRIkSnD9/nqeeeoqpU6fm2X7u2bOHYcOGMXPmTHx9ffOs3oJGErIQ2bBjxw6GDx+O1hqlFJ06dWLmzJkANGzYkM6dOxMTE0NQUBB9+vQhODiY27dvM2zYMOLi4rh16xbe3t54eXkxfPhwHvXw4IiICMaNG8eNGzdQSpGUlMSQIUPyaE8NGjdujI+PT57WWRBJQhYiG5o1a8aMGTPQWhMaGpruOlWqVAHAx8eHqlWrcvHiRdq0aUPx4sVTk3dm2Nvbo7Vm5syZ9OnTh2LFijFv3jySkpIYPnw4Hh4ehIeHU7NmTXr37k1ycjLvvvsuxYoVIy4ujtu3b/PFF19w+vRpPv74Y7y9vTlz5gyjRo3C09OTnj17Ym1tjY+PD/v27ePVV1/ljTfeAGDYsGEkJiZSrlw5Ll++/OQHTjySXGUhxBNQSuHt7Z3hsnuOHz/Oq6++yp49e2jZsiWffPIJANbW1mitOX78OMnJyemWY29vz86dOzly5AhVqlShcePG/PTTT3z11VckJCTwwQcfMGPGDCZNmsSNGzdYsGABCQkJjB07lo8++ojatWsD0L9/fwYOHIi/vz9vvfUWAwYMoHDhwgQEBHD79m2mTJnCqlWr+OyzzwDYtGkToaGhnDhxguvXr3P8+HE6duzIyJEjGTlyJB4eHhm27Pv168fhw4cfe/wiIyMZMGAAffv2fey6BYG0kIXIgoMHD7Jr1y4SEhJYvXo13bt3BwzJKywsjHnz5tG/f3927drF8ePHqVatGnXq1CEqKopZs2ZRtWpVQkNDeeuttwBo27YtU6dOJS4ujiVLlmRY77PPPsvSpUtJTk5m7dq1+Pn58dprr3H16tXUvuRq1apx7do1jh07RoUKFVK3HTBgAADHjh2jXLlyAFSoUIGjR4+mrnPvS6V48eJERkYCcPLkSSpWrMhzzz1Hv379+OOPP/jtt9+YMWNGakwTJkxIN96FCxdm6gSnq6srvXv3ZvHixY9dt0DQWmf6r3bt2loIkbcuXLig+/fvnzqdmJioCxcurKdOnapHjBiROn/t2rU6PDxcz58/Xw8ePDh1/ty5c7XWWjds2FAfOHBAa6313r179fPPP6+11nrHjh26T58+qeuXKVNGa631hg0bdJs2bVLn16xZU5coUeK+2EqXLq2DgoL0yy+/rPv166e11vro0aP6hRde0IsWLdK3b9/Wbdq00a1bt9b+/v7ax8dHr1u3Tv/000+6U6dOevLkyXrUqFH31Z8fAQd1JnKstJCFMHPu7u7cunWLESNG4O7uzoULF5g2bRr9+/fH39+fwMBAEhIScHR0pEuXLgwYMIB3332XwMBAkpKSqFatGgBfffUVQUFBVKxYkT/++IMFCxYQHx/P0qVLOXbsGAcPHuTEiROEh4ezZs0aunbtyubNm3n99dcpXbo0Wmuio6OJjIzE1dUVgJs3bzJw4EBcXV2pVq0at27dwsfHJ/VKjHtdIv7+/kybNo0RI0aQnJxM7dq1OXLkCJ6enixYsIAbN26Y6vCaFUnIQpi5woUL8/3336e77OOPP35onrW1NbNmzXpofpUqVVi0aNFD87/66qvU13Xq1LmvP3fOnDmpr/38/OjYsWNqMgbw8PBInS5WrBiRkZEULVo03boBPD09uXHjBjExMXh6egJQrlw59uzZk+7+FTRyUk8IkW2ZvREm7XrFihXD0dGRq1evAnD+/Plcic0SSQtZiCe0bds21q5di4eHB0opxo8ff9/yadOmce3aNTw9PTl06BATJ06kcuXKJoo2e2JjY/nyyy8JDw9n4cKF9O/fnwULFqR2bxQpUoSwsDAWLlzIyy+/nHpSs1mzZqldImvWrMHPzw8rKysWL17M66+/Tt26dVNPRO7Zs4fGjRubeldNShn6mzOnTp06+uDBg7kYjhCWJSYmBh8fH06ePIm9vT1+fn4MHjyYFi1apK4zbtw4Jk6ciFKKlStXsmzZMjZs2JBjMTzuCwFg1apVjBkzhk8//ZSOHTumzm/QoAEODg6Aoatj+/btORaX+JdS6pDWus7j1pMWshBPYO/evZQpUwZ7e3sAGjVqxKZNm+5LyB9++GHq65SUFFxcXHKs/piYGAYOHHjfF8L27dvvq//ChQsUL16c0qVLP7R927ZtU8fkEKYnfcj51OLFixk4cCDTp0+nZ8+e/Prrr6YOKV+6cePGfSe53NzcMrxiICEhgSVLlvDRRx/lWP0ZfSGkVbZsWZo1a5bu9sePH2fatGkEBgY+tJ3Ie9JCzqf+/vtvZs2ahYODA/v37+f111/n+PHjpg4r3/Hw8Ei9kQIM4054eHg8tF5CQgKDBg1i0qRJlC9fPsfqz8oXQnpGjx5NvXr1SE5OpmnTpri6utK0adMci09kjbSQ84EpU6bg6OjIzp07mTlzJu3bt6d79+6pfYM5/TNZ/Kthw4aEhYURHx8PQEhICB06dOD27dtEREQAhhNib731Fu+88w61a9dmzZo1OVZ/Zr8QMlKvXj3A0H/cpEkTduzYkanttm3bxuDBgwkMDEz3br24uDiGDBnClClT6N+/P3/++WfqMi8vL3x9ffH19aVXr16ZjrUgkBZyPjBmzBiSkpJYtmwZdnZ2rFmzBkdHR8BwJ+ann36apcFsROY5OTkxd+5chg0bRvHixfHx8aFFixb4+/tTpEgRAgIC6NWrFydOnODChQsAREdH4+fnlyP1p/1CsLe3JyQkhMGDB3P79m1sbGxwc3PLcNszZ84QEhKSemt1aGgoXbt2fWydmem3njVrFs888wz+/v4cP36cAQMGsHv3bgD69u0r/dYZkIScT7z//vtUrVqVoUOH3peMR40aRd++fWnYsKGJI8y/WrVqRatWre6bFxQUlPp67dq1uVZ3Zr4QtNZMmjSJsLAwVq5cia2tLW3atMHNzY2NGzdy5coVIiIiKF26ND179nxsnZk5kblp0yYmT54MQPXq1Tl69CgRERG4ubmxa9cugoKCiIyMpF27djz//PO5c3AsUWbur9YyloXZ++677/SiRYt0lSpV9Llz53RSUpIeOnSoDg4OTl0uRE5Yvny5fumll1Kn//e//+levXrdt463t7c+fPhw6nSpUqV0aGio1lrr/fv3a621jo6O1pUqVUqdn58hY1kUHAsXLmTu3Lls3LiR7du306VLF4oUKcK5c+c4duwYAOfOncuxn8miYMtMv/Wj1rnXb+3k5ETNmjUJCQm5b3S6gkwScj7Qv39/+vfvD8DSpUtNHI0AQz/x7Nmf85//9OLpp582dTg5KjP91h06dGDv3r00adKE48ePU6NGDdzc3Ni+fTuJiYm0bdsWgLNnz+boVSeWTu7UEyKHXb58mZZtO3AlKgW72H/YvPEH6tata+qwctTWrVv57rvvKF68OLa2towfP/6+fuvY2FhGjhxJyZIlOXv2LO+99x7e3t4cP36cwMBAateuzZUrVyhVqhRjxowx9e7kuszeqScJWYgc9Ntvv9GuYyd4th3OdbsSG7qPmF++YMG8ufTo8YpJYtq8eTPjP5zCvM9nUatWLZPEUNBlNiHLdchC5JCVK1fRrFUbrBoNwKWeH0opnLwb4tZlAm8M+S/jxgeSlQbQk9JaM/OTT+n+6muE2palafOWOXoNtMh50odsoWRAGfOhtWb8hIl88vk83LpMwK5EufuW25Uoh3uP6Xy+ZAonT53mm68Xp16amFsSExN5c9DbrN28jUI9pmHjXoJ4r+fo8+ZgTp0+w9j338v00Jki70hCtkAyoIz5iI2Npddrfdnx23EK9ZiOtUvhdNezcSmCq99H7Nw2m/qNmrLlxw2pA7TntDt37tDxpa6cvhmL+8vTsLJ3AsC+ZEWsewTx8ZeTOXHqNF8v+ir1WuKcdu7cOf755x/q16+fK+XnV9JlYYFkQBnzcO3aNeo3asrOP2/g6vdRhsn4Hitbe1zavssV10r41Kpz30NGc0poaCg1atXlj4TCuL74XmoyvsfGtRhu3Saz7dhfNGziy82bN3M8hi1btvBcnfo0b9OBoOkz8rSbxtJJQrZAOTGgzOjRoxk3bhyTJ09m165duRFmvnb06FF8atXhimslXNq+i5Vt5lqaSilcGvZE1+1FoxeasX79+hyLaceOHdSp35DYyu1w8R2AsrJOdz0rOwdcOoziL3svfGrV4cSJEzkWw2ez59D1lVdxaj+Kwq9OZ/Kn83mt3wASEhJyrI78TBKyBTLVgDLCYP369TR+oRm6bi9cGvbMVl+sc5WmuHYaS69+bzBpytQnbkXOmz+fF7t0w6HNOzjXaPvY9ZWywqXRf0iq2Z2GTV544l9KSUlJvDloMOOmzMD95ak4lK6GjZsHbt0ns+nAGZo0a8mtW7eeqI6CwGISstaa+V9+ybVr13KtjuDgYLp27cr06dPp3bs3CxYsyNHyo6Ki+HzOHGJjY5+onLQX5l+/fp1ly5bRrl27+0YYy8j27dvpbxxMBgw/ceUuqczbt28fXbp0Qdu7Yh35hJ/FiGvYuBVn7HtjmDN3XraLWblqFYMGDsTKpShWEVeztK111A1SbJ15sVMnnuSS1ndHjeZ/8+Zi41qU5Ih/f62lxEdjbWPLb/v30qpt+2yXX1BYzEm95ORkBr71FuMCJ7J18yZq1KiR43XExsYSEBBAvXr1uHPnDiVLlqR///5YWT3599alS5do0aY9oadP0KJ589Sn8GZH2gFlrl+/zuHDh/l41mwqVyyHp6dnhgPKuLq60qVbd6IjIynr5ZWlAWWEgY+PD6tWreLOnTuM8H8Ph3ovZ7uslNDdDOrZidq1JzzR4E8tmjdn9erVhIaGMvN/32Bf/fEt5HsiDm3g81kf4+bmRrVq1bIdw9uD3qJJo4Zs2rSJDacOQBnD/2f8lT942i6WuSu+5amnnsp2+QWFxbSQAaysrNF1XqVxDvS9pTeGcPny5VN/zp89e5ZKlSrlSDI+cOAANWvX5U7JehQqWeaJywPDCGPz58/n5Zdfpli1Jhy8msDmrb+kji+rlGLs2LFcuHCBpUuXcv36DVq3fxH7Jq9j7+DAuHHjmD59OrNmzcqRfSwonJyc6Nat232XET6Jxo0b061bN0qVKpXtMooVK0a3bt1o3rx5trbv1KkT3bp1S70UMju8vb3p1q0bNWvWfGhZiZKl6Natm4zqlgkW00K+x7nqC9gU8qRXvzd4z/8MY0b7Z6sP71FjCE+cOJGNGzcyf/78J453+fJveXPQ2zi1HIJTxfqEn/nlict8kJWNLQ6thnD74Dpq1q7L5o0/pH6xpKSkMHrM+8xb9DVufh9i41aM6JwPQQiRAyyyaWT/VCUK9Qgi6PMF9Hqtb7bP4L7//vvs3r2bqlWr3neh/gcffMDmzZvp3r17lq5eSEtrzfvjPuCtYe/g5jcBp4q5ez2mUgrnul2xbvImzVu15dtvVxAdHc2Lnf1YsHoThXpMx654zrTOhRC5wyITMoCNW3HcXp7Cz7+fo9ELzfnnn3+yXMa6desICAhgzpw5nD9/nrlz5xIVFQVAkSJFsLGxyVZCjo2NpXO3l/li2VpDIvQo9/iNcohTxfq4+U3gzaEjqFi5KvsuReHWdSLWTu55FoMQInssrssiLSs7R1w6jubCnqXUqFWXbT//mOmTZemNIdy1a1eGDh1KpUqVuHDhAv369cvyiY6rV6/Suv2LXElxw83vQ5SNXXZ27YnYeZSjUI/pxF85g0vFBnKLrBAWwqITMhivp2zSh6jjpaj/fGNWr1hOmzZtHrtdbowhfOTIEVq370hKxWa4NHjFpInQ2qUwTt7y2CYhLInFdlk8yKV6S5za++PXoxezPp2d5/WvW7eOxr7N0XX/g0vDHtIqFUJkWb5JyAAOpavh/so0xk/7hNffHEhSUlKu16m15qPJU+j9+kBcXxqHc5UmuV6nECJ/svguiwfZFvLE/ZWprN38MWdatmHj92soVKjQQ+s9bvhKrTWzZxta2hcvXuTu3bssXLjwvnXi4+Pp0/91ftp1gEKvBGHjViz3dkwIke/lu4QMYGXvjGun9zmzcyE1a9dj288/3nd7cGaGr1y2bBmFChXitddeA0h9WOg9N2/epG3Hl7gYZY1b98lY2WX/onohhIB81mWRlrKyxqXZG0RXbE2d+g3ZuXNn6rLMDF/5zTffcPv2bT777DPee+89XFxcUpedPHkSn1p1CLN9BpeO/pKMhRA5It8m5Huca7bDvtVwOrzUlf8ZBwvKzPCVYWFhREREMGzYMPr27Uvbtm1JTk5m8+bNNGzclKQafrg07o1Spj2E1tbWkJKc+Q2sbEiUoRCfWFxcHFY2tk9Uhk5JMbx/Qhjl+4QM4OhVE/fuk3l37ESGjXiXokWLPnb4Sjc3t9SnHXh7exMREcH4wAl0f/U1nDoE4FytBebAwcEBkhMzvb6VrT0oRXh4eC5Glf9dv34dWyfXx6/4KMkJuf4oJ2FZCkRCBrAt+jTurwSxbOMOpgR9zIULF4iPjwcgJCSEDh063Dd8ZYsWLTh//jwAt27d4m54OJ999TWFekzD4emqJtuPB3l4eJAcdTtL27h712X58m9zKaKCYcnS5VD6uScqIzk+Bmdn5xyKSOQHBSYhA1g7uuLaeTzH71oTl5hMv379GDt2LD4+PrRo0YKpU6fyxRdfAIanahw5coRx48ZR9dlq2BYrQ6FXpmPjXsLEe3G/GjVqEHHtIjoLrWTrZ9syY9Zn8midbIqOjmbpsqU4Vn/8DUgZ0clJRF6/ROXKlXMwMmHp8uVVFo+irG1wbjGYmN9/4Ket69n0w9DUsWiDgoJS13N3d2fkyJG0aN2OZK+GFGnaN8NH4piSk5MTT5UuQ/zNMOw9MzfQvEMZH/4J/pLvv/+eLl265HKE+c+nn83G8emq2Lhn/iktD0r85y88Sz1938liIQpUC/kepRTOtV/CxncQrdp1ZOnSZQ+t88svv1CnfkNiHvN8MnNQr25dEq6dzfT6Slnh2HIor/UbwL59+3Ixsvxn1apVTJ4+E7sm/Z+onPhrZ6lbp04ORSXyiwKZkO9xKl8XN7+JDH5nNKPHvE9KSgoAc+fNo1PX7ji0eQeXTDyfzNQ6tm2FCvstS9s4PF0Fp1bDaNm2PfPmzXvix0rld3fu3OGDwEAGDBr34/OvAAAgAElEQVSK20vjsC3k+UTlqVvnadKwXg5FJ/KLAtdl8SC74l4U6hHElyuncvL0aZ4pXZplq7/H/eUp2BbJ/lMc8lL37t0Z8t8RJN65im3hkpnezrF8XaycxzP2syX4j3mfvn368NKLHShcuDA2NgX+o0FCQgI3b95k2YpVrFu7FqfydXB/eeoTdVUAaJ1CYtgRmjQJzJlARb4h/3WAtXMh3LpOZF/wl+w/exD3HkFYO1hO356joyP9+/Vl2b6fsW3aN0vb2ntWwL7TWBLvXmP5gZ9YsXkUyXHRoFNyJ1gLoqxssHJwJtmzGkX7foG188O34GdH3IXDlChWmFq1auVIeSL/kIRspGzscGk5xNRhZNuwIW/zv6/q4FS/O1b2Wb+UyraQZ5aTucielJM/M/K/Q2VEQPGQAt2HnJ+UK1eO7t38iNm1yNShiEdICr9B7OVT9Or1qqlDEWZIEnI+MnvWTKyvnSD2/CFThyIyEHt4A//p9R+5IUSky6ISssbyb2RQyork5CyMPZEFrq6ufLNkETG/fEFKXFSu1CGyL/7qnySH7mbC+LGmDkWYKYtJyNbW1uiUFIu/u8zawZm7d+/mWvktW7akz6s9iNwwmZTEuFyrR2SNTkogZutsvpj9GSVKmNfdnsJ8WExCVkphZZXFkc3MkC7qxU8/b8nVOj6bNZNW9aoRtWEqKQmSlM1B9N4VPF+rOj179jB1KMKMWUxCBrBzcERbeKvPrlobvpj/JYmJmR97IqusrKxYvnQJbepVIXLdeJKyOPiQyFlxYcdIPP0Li7/6Uq6sEI9kUQm5SLHiJEffMXUYT8SuuBdW7p589913uVqPjY0N33y9mEG9unJn2XCiTu6w+O4eSxR/9U8if5zOuu9W5npXRXJyMmQx32u53tysWFRCLuFZkuQoy07IADb1evLW20M5efJkrtZjZWXF5I8msmv7Ftz//JGojVNIirjx+A1Fjoi/8geR6z9i+deLaN68ea7XFx4ejsriNejJiYmGMbWFWbCohFyq1FMkRd0ydRhPzKF0Neyb9KdRU1927dqV6/XVrl2bU8cO82bn5txZNoKojVOIvXBYWke5KPbikdRk/NJLL+VJncG7dpPilvnb/XVyIslJiTJIvhmxqITs9czT+aKFDOBc5QXsWwylfedu1G7QiBUrVpCQi49Wsre3Z8qkD7l+5TIfDemN69FvubvkbaK2zyXy6M8kXD+PTk7KtfoLipTEOKKCvyJx+2dsXL+WTp065Um9CQkJzP9yAfZZGKM54WYYpcuWl8dImRGLunW6zNOlsNp30dRh5BjHcrVxGPA//jq7nyEfBPGf3q/h5OKGrZ1dHtSuibhxDa5fSndpmdEb8yCG/CXu8ilits2mRZOGLNh0iqJFi+ZZ3atXr8am2DPYFn0609skXDtL4zq1czEqkVUWlZArVaqEdfgqU4eRo5S1Dc6VGkGlRjgnJ5ISF5VnLdUHf9zqpAR0YjzKTn7CZkXiP5eIO7IBHXaQxfPn0rVr1zyt/88//+TtYcNxaPNulrZTty7QuF2rXIpKZIdFJeTatWsT9Xcojlrny8uHlLUt1s6FTR2GyASdnERM6D70qZ9JunWZN98YgP/IJRQrVixP4/j9999p1a4Dtg164fBM9Uxvp7Um6e+TNGgwLhejE1llUQn5qaeewt7OluSIm088Jq0QWZESH03CtXPEXzuL7Z0LxIQdx9u7IqMmjMLPzw+7POlmMsaSksL27duZ/sln7Nm9G5eWb+NU6fkslRF/+SRujrbUqyeD5JsTi0rIADWeq8Wpa2clIYtcFzatY4bLnF3diImNZcKUICZMCcpwvZwWHxfP7X9uYuVcCKtn21LsjT5YZaOLKenETwQMeztf/tK0ZBaXkJs0rM+x7Wcgiy0CIbKqWOcx6PgYlK09Nm7FQd1/UVK4CWJSNra4Orhi7Vos28k0OeoOMed/p2+fdTkcnXhSFpeQGzaoz7wVP5g6DFEAOFdqZOoQckXsr1/Tt08fChXKmSegiJxjcQnZ19eXqL9DcYiLsqjHLAlhDmLO/YbtzT8ImrrW1KGIdFjUjSEATk5ONGzclLjzB00dihAWJTkuiphf5rL868W4uOROY+ah8VJk/JQssbiEDNCzWxf4S56KIURm6eQkord8Ss9uXWnWrFmu1RMZGUmytf2/9aYk4eBg/4gtRFoWmZA7duxI1NlD6OTcG8JSiPxCpyQTtXU2Pk+5Mmf2p7la17FTZ1BprqVPibiBV+nMj69R0FlkQi5ZsiTlylcg7q/jpg5FCLOmkxOJ2vwxld2S+fGHdbl6vfSdO3fYtHEjzpWbpM6zuXORBvXq5lqd+Y1FJmSAQW/2J+X0dlOHIYTZSrh5kfCVo6lftgjbt2zGyckpV+v7auEinCvUxdrZcPWGTkokOuwEDRo0yNV68xOLTciv9e5NzMUjJEVa/nCcQuQknZxE1L6VRK4Zx/Rxo9i0fm2uj3l84cIFJk2dhk319qnzYv78FZ8aNfDy8srVuvMTi03Ibm5uvPLKK8Se2GrqUIQwCynxMUQe/pHw5SOoanWVU8eP8sYbr+f63Xjnz5+nSbMW2DzXBfunKgGGfuukIz/gP2JYrtad31hsQgYYMWwICSe2yDi+osBKiY8mLuwYUb/M558Fr1PX9jLfLfmSndu3ULp06Vyt+/r160z48EOeq1uf+Eptca71Yuqy6IPfU7mMJ507d87VGPIbi7sxJK3q1atToXw5Lofuw7lyY1OHI0Suu/RpT1LiItNd9vrrr/P0008TEhJCSEhIrtSfkpJCRGQUp/88y66dwThVaoRzpw+wK1EudZ24y6eI//17vj3yu4yVkUUWnZABAt8PoM/gd9DeDVFW8uQDkb8paxuUjT1WTu7Ye1bApujTKGX43K8+FQ2n/sj9GGztsXYuT7EBr2L1wN2ycZdPEbVxKt+tWC59x9mgsvIk4jp16uiDB83rDjmtNc/VbcBlz8a4VMv9B0kKIR6mk5OIOvAdCUd/5LuVy2nTxvAoqbNnz7Jg0WImTZxQoB8VpZQ6pLWu87j1LLoPGUApxexPZpCwfwU6SW4UESIvpSTGEXl0C+Hfvsuz1tc4dfxIajIGOHz4MNMmT+Jd/9EmjNJyWHyXBUCTJk2o81x1jh3djEvtvHmopBAFUVLEP9z4LpDkyH9IiYtKnd+5c2fatm3L5s2b71v/4MGDFK7wHAuXraT6s1UZ0L9/XodsUfJFQgaYNSOIhk2b4fRs84f6tYQQOUMnxpF48yIAtq5FcX66ErbOhQi5nEDIgvSHxbWv3QVH1+L8951RVKxQgaZNm+ZhxJbF4vuQ0+r3+ptsOPwXLq2GmjoUIcQDYi8cJn7bpxw6sI/y5cubOpw8VWD6kNP67JOPsb52kthz5vulIURB5Vj2OWzqdKdlm/aEh5vieSvmL18lZFdXV5Z/vZiYX+be178lhDAPLs91IKJIJV7s0o2kJLmh60H5KiEDtGjRgm5dOhGze5GpQxFCpMPF93VO/H2Xt4f919ShmJ18l5DB0HVhc/0U0X/kzt1KQojsU1bWuLQbyYp1m/h8zhxTh2NW8mVCdnV15ccfvid2x3wSbpw3dThCiAdYObjg0mksAWPHs2XLFlOHYzbyZUIGqFWrFv+bO4fIDVNJjpETCEKYG9vCJXFpP4pur7zKmTNnTB2OWci3CRmgZ88eDOz/GtGbguRxT0KYIYfS1bBv2IuWbdpz65aMbZ6vEzLAtCmTqO1diqhf5j/8RFwhhMk5+7QmrlQt2nfqQkJCgqnDMal8n5CtrKxYu2oFJZNvEL1rsSRlIcyQc+PXOHsnmQFvDizQ/6P5PiGD4STfrl+2UiT8D6JDlhXoN1wIc6SsrHFuO4IN23YzfcbHqfMPHDiAr68vzz//PIGBgQQGBhIQEMDw4cNzpN7g4GCOHDkCwKVLl/Dz8yMwMDBHys6OfDOWxeMUKVKEkJ2/8HzTZtzZvQTnJn1k8GwhzIiVnSMund5j4hR/qlSuxIsvvki9evXw9fUlKioqNVHGxcWxbdu2HKkzODgYLy8vatasSenSpXnxxRe5ePFijpSdHQWihXxP8eLF2R+yC4+os4Y+5ZRkU4ckhEjDxs0D1w4BvPpaX44fP/7Q8qSkJAICAujYsSMffvghH3zwAWPHjmXixIkArFixgkKFDE+9PnDgADVr1iQ4OJg7d+7Qtm1b2rRpw+jRo6lRowZBQUEEBwfz/fffExgYSFxcHGAYw9nf35/GjRuzadOmvNt5ClAL+Z4iRYqwd3cw7V/szOn1H+HS7l0ZHU4IM2JfqjJJTfrTql0Hjv1uGJdmx44dDB8+HK01Sil+/vln9u/fz8aNGwFo164dW7ZsoUePHgQEBABQr149atasCUDhwoUJCAjA39+fadOmMWLECJKTk4mJicHLy4u+ffum1q+1JigoiIMHDzJhwgQ6dOiQZ/teoFrI97i7uxO8fQvdW9Tj7gp/Em9dNnVIQog0nKv6klS2Ma3bv0hSUhLNmjVj1qxZzJo1i8GDB3Ps2DHKlfv3OX4VKlTg6NGjjy23SpUqAHh6elKqVKl016lQoQIAxYoVIzIy/ecX5pYCmZABbG1tmf/F50yf+D7hq98j9vwhU4ckhEjD+fmeXIp3YO3361NPxCul8Pb2pkaNGpw7dy513dDQ0NTWsKurKxEREQD89ddf95X54Hkja2trtNb8/fff3Lx5M9118lKBTcj3vPXmm/y0cT2JO+YQtftreQyUEGZCKStsfdrz59nzrP7uO1avXp26rHXr1tSvX58xY8YQEBBAw4YNadWqFQBDhgxh6NChzJ07FysrK5YuXUp4eDhLly7l2LFjrFmzJrWcpk2bsn79ekaNGkVMTAwbNmxg165dnD17lsWLFxMWFsb27dvzbp/z0wD1T+L69ev0HfAmv/5+HKdWQ7Ev6W3qkIQQQFLkLe6u8GfRvM/p3r2bqcPJlgI5QP2TKFGiBD9u+J65MyYRs2GytJaFMBM2rkVxfXEM/d54k0OH8nfXoiTkNJRSvPpqT/48fYK6heO4u3wEMaH75EYSIUzM3rMCdrW60P+tQaYOJVdJQk7HvdbyN1/OxvXEGiJXjyHu0glThyVEgZUU+Q+JRzfxwZjRpg4lVxW465AzSylFx44dadeuHd988w3+Y8YS6fYU9g16YVei3OMLEELkiJTEOKI2TMF/xFD8/PzSXWfbtm2sXbsWDw8PlFKMHz/+vuWLFy9m3rx5ODg4ADBgwAB69+6d67FnlZzUy6T4+Hi+mDuPDydNxqrQU6iqbXDyboCytjV1aELkW1qnEPXjDFpUe5qVy5ele0laTEwMPj4+nDx5Ent7e/z8/Bg8eDAtWrRIXWfx4sX4+vri5eWVh9H/S07q5TB7e3tGDP8v169cZu7k9/C6GcKtBW8QuWcZSRE3TR2eEPlS9K/f8oxDPEsXL8zw+uC9e/dSpkwZ7O3tAWjUqFG6tzx//vnnzJgxg4kTJ3L79u1cjTu7pMsii2xtbenevTvdu3fn1KlTfPr5HJYt/S+OHs+QUro2DhXqY1u0tAxcJMQTij61A5sLe/j594OpyTY9N27cwNXVNXXazc2NGzdu3LfOCy+8QIcOHShevDg//vgj3bt3z9PrizNLWshPoGrVqsz/Yg63/7nB8rkf41fJkcRNH3F3ySAig78iJnQfSZH/yFUaQmRR/N+nidu9iG0//YiHh8cj1/Xw8LjvFueIiIiHtilbtizFixcHoHnz5uzcuZPkZPMbXEwScg6wt7endevW/G/+XG5cuczOnzYwtF1NvG/vJWL5O9z6si8xGz4iYs8yYv74lfgrf5AUcROdnGTq0IUwO0nhN4jcNI0Vy76mWrVqj12/YcOGhIWFER8fD0BISAgdOnTg9u3bqbdQjxkzhqQkw/9baGgoZcuWxdraOvd2IpukyyKHKaWoWbMmNWvWJHC8YeSoS5cucejQIfYf+I0Dvx/mytkr3Lh+jYg7t7F3csHBvRjWDs5gZQNWViiVN9+TOiWZqOthxN65/+edtUsRnn776zyJQYi0UuJjiNowifHvBWR6lDUnJyfmzp3LsGHDKF68OD4+PrRo0QJ/f3+KFClCQEAAnp6eDBo0iLJly3L8+HGWLl2ay3uSPXKVhQklJydz8+ZNrly5QkREBElJSSQmJuZaF4fWmpCQEFauWs35c2dT51s7OGPjUQ5r5yIoG1scnq6Ki0/rXIlBiIzolGQiN06hY/2qLFm4IF+dh8nsVRbSQjYha2trPD098fT0zNV6IiMjWbp0GR9/Opt/wqOxruRLibr9sStRTsaCFmYjevfXeBex46sv5+WrZJwVkpDzsbCwMCZNmcY3y5fjWKY61s/1olAZnzzrEhEis6KPbcHx6mF+/P03bG0L7rX9kpDzIa01c+fNY/SY97F7thWF//MpNm7FTB2WEOmK++s4Cfu+Yc/eEIoUKWLqcExKEnI+ExYWRs/efTkddh1Xv4+wK17G1CEJkaHEO1eI2jyDdau+pVKlSqYOx+Tkt2s+ca9VXK3Gc/xp7YXbK1MlGQuzlhIXRdQPk5g2aWLq4PIFnbSQ84GUlBQGDRnGyh9+llaxsAg6JZmoH2fQs8uLvD14sKnDMRuSkC1cUlISvV7ry5Z9x3Dr9pFcNSEsQnTwAqqXLsznn31i6lDMiiRkC5aSkkLvvv3ZevAMrl3GY2XrYOqQhHis6MObcL3zJz9s3Y+NjaSgtORoWCitNUP+O4Kffj2Ma+dAScbCIsRe+J2kQ9+x/cA+3N3dTR2O2ZGEbKGWL/+Wb75bj9sr07Cyk2QszF/iP5eI/nkWmzd8T7ly8pCH9EhCtkDXrl1j8ND/4vTie1hLn3GuuflDEEl3rmJTyNNwV6Odo6lDskgOz9TAysmNyA2TmP3JxzRp0sTUIZktScgWRmtN3wFvYlu1BfYlvU0dTr4We/4gOj6GhGuhxJzZnTq/qW8zKlSUY58ZF86f4/i+4yTFRvF67x7069fX1CGZNUnIFmb58m/Ze/gEhV6daepQ8r1nhq9Kfa2Tk0i89Rfxf4Zw6Mg2EpI1QZMmSmvvMVavXs0rr/SgVdv2zAiaZupwzJ7cGGJBbt68yeChw3BqNRRlU3Dv9zcFZW2DnUc5XBv3puiABYS61aLdS368NfhtoqOjTR2e2Spbtiyt2rZnzapvsbKSdPM4coQsyBfz5mFbtq50VZiYsrHFpVpzCvf+jO9+/QPvqtU4ffq0qcMyS3Xq1OHnHzfg4iLnOjJDErKFSEpK4vMv5mHn097UoQgja0dXXNuOIKF6F55v8gJHjhwxdUjCwklCthCbNm0ixbEIdiXkciFz41ytBTaNB9C8VRvOnj37+A2EyIAkZAsR9MlnqGfbmDoMkQHnyo1RNTvTpXuP1Ge3CZFVcpWFBQgNDeXI4cMUe2NIrtajkxNJCr9BSlwU6JRcrcsiWNlg5eCCTaESmRrU36VWR/5ee5Bp02fw/piAPAhQ5DeSkC3Axo0bcfRuiLKxy5Xyk8KvE3vsZ+JObsPN1RX3QoWwljEGSExI5M7tW0Qlg0211jhVa4m1U8a3+yplhVPLt5kybSSv9niFsmXL5mG0Ij+Q/zoLsPvX/ehiFXK8XJ2STPTuJcSf3kGf115j2KK9eHvLFRwP+u233/j409msXzgQl+d74VyrY4br2riXwKFqC2Z99jmffvJxHkYp8gN56rQFKF2uIsm+w7DzyLkTelqnEP3zLMo7J/LTxvUULlw4x8rOry5cuECzlm2Ifro+zg17ZLhe4p2rRK4azfUrl3F0lNutReafOi0n9cxcZGQk16/8jW3RZ3K03Ji931LGPpad27dIMs6ksmXLcmDvHuwu7CH61I4M17MtXBI7zwqsW7cuD6MT+YEkZDN35MgR3J4qi7LOud6llLgoog5vYsO673BwkJHissLDw4NV3y4j4cAq9CNOfKY8VYPtO3bmYWQiP5CEbOaOHj0KRXP25FD0yV9o3bo1Tz31VI6WW1A8//zzlCjiTtzFjG8EsfMsz94D0r0nskYSspm7e/cuyXbOOVpmyqmtvPvfoTlaZkGilOKdYUNIObU1w3XsSpTn3J+n5ZpkkSWSkM1cdHQM2jrnLnfTOoWIa3/RqFGjHCuzIGrSpDFJty9luNzKzhFlbUNkZGQeRiUsnSRkMxcTF4eyzrmR3XRCHLb2DlhbW+dYmQWRu7s7ibGPHuXNxtaOuLi4PIpI5AeSkC2CysGyNFZWOVlewWRtbQ2PvWRUjrPIGknIQghhJiQh5xMp8TEk3rlq6jCEEE9Abp3OBxLvXCHqh0kkRN7CpWk/nH1kVDghLJG0kC1c3F/HCV81hkljR3H090M4nNpE1M6F6JRkU4cmhMgiScgWLPrYFmI2z2DtyuUMefttvL29Ofr7b1S0uUXkximkxMeYOkQhRBZIQrZAOiWZqF2LsD+5gQN799C6devUZUWKFGHXL1t5scGzRKweQ1L4DRNGKoTICknIFiYlPobIjVMpr25w9PffqFy58kPr2Nrasvir/zF2xGDurhxN3GV5AKcQlkASsgVJCr9BxOr36FCvMrt3bKNo0aIATJkyBUdHR3bu3MnMmTNp3749oaGhjHz3HVYuXUT0pimPHJ1MCGEe5CoLCxH/9xkiN01l/HsBjHz3HZT696aDMWPGkJSUxLJly7Czs2PNmjWp4/B26NCBvbt30rJte6Ju/41jnc6m2gUhxGNIC9kCxJ7/jaiNk1nx9SJGjXz3vmR8z/vvv8/u3bupWrXqQ4OiV6tWjWO/H+SZhItEbZ6ZV2ELIbJIErKZc3dzwz3pDr/uCqZjx4wfHbRu3ToCAgKYM2cO58+ff2i5h4cHe3cH06pWBVxd3XIz5HwtNDSUBk2a0eElP3jcGNXWNnR4yY8GTZoRGhqaNwEKiyYJ2cxNCBzPhdA/qF69eobrLFy4kKlTp9KuXTtq165Nly5d2Lnz4cHR7e3tWbl8GRfOSXLILnt7e65fvcLpSzdx7zz+keu6dx7P6Us3uH7tqjwIQGSKPFNPiCwKDw/nxS7dOPH3XVzajcTKweWhdVLiooj6cQbVSxfmh7WrcXfP+GnVIv+TZ+oJkUvc3d35ZctmXm7RgPCVo0m8c+W+5Yl3rhC+0p9XWjVk+88/SjIWmSYJWYhssLGxYd4Xs5k8zp/wVWOI++s4AHF/HSN81RimfBDA3DmfYWMjFzKJzJNPixBP4O3Bg/GuWJFur/Qk1qseXDzA96tX0LJlS1OHJiyQJGQLsW3bNtauXYuHhwdKKcaPv/+E0rRp07h27Rqenp4cOnSIiRMnpt7F5+XlhZeXFwClSpXim2++yevw87VWrVpxYG8I4yd+xIRvQ6hUqZKpQxIWShKyBYiJiWHgwIGcPHkSe3t7/Pz82L59Oy1atEhdJyoqipkzZ6KUYuXKlYwaNYoNGzYA0LdvXwIDA00UfcFQqVIlVnyz1NRhCAsnfcgWYO/evZQpUwZ7e3sAGjVqxKZNm+5b58MPP0y9YSQlJQUXl3/P/O/atYugoCDGjRvHr7/+mneBCyGyRFrIFuDGjRu4urqmTru5uXHjRvqjuCUkJLBkyRLmzJmTOm/q1KnUq1ePmJgYatWqxcaNG6lQoUKux50fHDhwAH9/fxISElJH1YuLiyMuLo49e/awf/9+rK2tOXHiBFOnTsXb2xtbW1scHR0ZPnw4AJs2bWLIkCHs2LEjtetIiPRIQrYAHh4e9z1OPiIiAg8Pj4fWS0hIYNCgQUyaNIny5cunzq9Xrx4ATk5O1KxZk5CQEEnImVSvXj18fX2JiopK7faJi4tj27ZtfPLJJ6m/StavX0/z5s3p378/iYmJVKxYMTUhd+jQgenTp5tqF4QFkYRsARo2bEhYWBjx8fHY29sTEhLC4MGDuX37NjY2Nri5uREbG8vgwYMZOXIkzz77LGvWrEnta05MTKRt27YAnD179r5kLbImKSmJgIAAmjdvTtmyZQkODiYiIoKtW7dSqFAh4uLiKFasGHfv3iUwMJDKlSvTo0cPAFatWsX58+c5ffo0GzZswM1NbmEX95OEbAGcnJyYO3cuw4YNo3jx4vj4+NCiRQv8/f0pUqQIAQEB9OrVixMnTnDhwgUAoqOj8fPzw8PDg8DAQH7//XeuXLmCn58fjRs3NvEeWZ4dO3YwfPhwtNYopejUqRMzZxoGavLx8cHX1xcvLy/69u0LgL+//0MnUp977jn8/f0ZMmQIW7duxc/PL4/3Qpg7ScgWolWrVrRq1eq+eUFBQamv165dm+521atXZ82aNbkaW0HQrFkzZsyYgdY62wMF3esmKlas2H1dUELcI1dZCJEFSim8vb0fu561tTVaaw4fPnzftkI8iiRkIR7h4MGD7Nq1i3379rF69erU+Zs2bSIsLIx58+Zx4sQJdu3axYYNG9ixw/Bklg4dOjBy5EiWLFnC1q1bCQsLY+HChZw/fz513Zs3b5pqt4SZktHehBAil8lob0IIYWEkIQshhJmQhCyEEGZCErIQWbRt2zYGDx5MYGAgEyZMSHedVatWUb58eTZu3JjH0QlLJtchC5EFmRl578KFCxQvXpzSpUubMFJhiaSFLEQWZGbkvbJly9KsWTNThCcsnCRkIbIgKyPvCZFVkpCFyILMjrwnRHZIQhYiC9KOvAcQEhJChw4duH37NhERESaOTlg6OaknRBZkZuQ9rTWTJk0iLCyMlStXYmtrS5s2bUwdurAAcuu0EELkMrl1WgghLIwkZCGEMBOSkIUQwkxIQhZCCDMhCVkIIcyEJGQhhDATkpCFEMJMSEIWQggzIQlZCCHMhCRkIYQwE5KQhRDCTEhCFkIIMyEJWQghzIQkZCGEMBOSkIUQwkxIQhZCCDMhCVkIIcyEJGQhhDATWXqEk1LqJhCWe+EIIUS+VEZrXfxxKxwv3nIAAABGSURBVGUpIQshhMg90mUhhBBmQhKyEEKYCUnIQghhJiQhCyGEmZCELIQQZkISshBCmAlJyEIIYSYkIQshhJmQhCyEEGbi/6OFgHxngdD2AAAAAElFTkSuQmCC\n",
- "text/plain": [
- "<Figure size 432x288 with 1 Axes>"
- ]
- },
- "metadata": {},
- "output_type": "display_data"
- }
- ],
- "source": [
- "# Libraries\n",
- "import numpy as np\n",
- "import matplotlib.pyplot as plt\n",
- "from matplotlib.sankey import Sankey\n",
- "\n",
- "\n",
- "snk = Sankey(flows=[0.25, 0.15, 0.60, -0.20, -0.15, -0.05, -0.50, -0.10], \n",
- " labels=['x', 'x2', 'x3', 'First', 'Second', 'Third', 'Fourth', 'Fifth'], \n",
- " orientations=[-1, 1, 1, 1, 1, 1, 0,-1])\n",
- "\n",
- "snk.finish()\n",
- "\n",
- "plt.title(\"Sankey diagram with default settings\")\n",
- "\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 247,
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [
- {
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAhcAAAFoCAYAAADkRdnBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsnXl8HHd999/fmT1Gq5VkW769iu3ESezcTkIgJIDD0VJouUppIBzhKTeU43HhgbZAAjScgbacpQVCHq4UeJpQ7qOYQCAXuRPHic9ofVuHpZU02mO+zx/fWWslrw7ba1uWf2+/5jXy7Fy7szu/z3xPUVUcDofD4XA4GoV3vE/A4XA4HA7HzMKJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNxYkLh8PhcDgcDcWJC4fD4XA4HA3FiQuHw+FwOBwNJXG8T8DROAphrhdoqfNSBbjjGJ+Ow+Fw1EV+zpP9t+DXeak/yOdnHfMTcjQcJy5mFi2A1lmeADqP8bk4HA5HXXQOlwFRnZfqPRw5TkCcuDh5ePLxPoGjgNZMUc187N+VMX/XE2AOx7FBESJ8InwUH8U7aAKp+b8c71NuNDI8896TYzROXJw87AUKx/skGozEk1czHyswNH6N+HUfKAP7ge542gPsBPYBPTXLe7JBvt7TlcNxEOH1OQFmA/OBefHfi4DFwAIgB2SBZAR+WWiqiKRUSEaCH4FXEfEjwauISCTEk8hMU8OlPjiV8vE+DcdRxImLk4f9QNfxPolpggckgbnYzf8CIIUJkUrNOhTC3D4gD2yLp12YENmVDfLhsT1tx/EmFhCtmGBYBCwFzgBOwwREAKSBVARS8qDoCUO+5w0mJNmT8mV3U8LrSnuyP+UX96e8Yl/SKw4kPB1MeAx7Ui76Ui6LVMoe5ZInlbJIRWVGWdukY2Ppiq+y63ifh+Mo4sSF42QkAobjaSIEGyjOAM7Dfi9Vt0qiEOZ6gK3AemATJkLy2SA/0yxEJyXh9bkkZm3oAFYA52LfgwzQhAnSCjBUFkr7k95QZ3Oy98HZ6dSDs9OtOzOJTE/KH94X+OV9aT8aSngh9p0LgdJxeVPThGzCGQRnOk5cOBzjo9hAEGKWn7GkMOFxQfz/CPALYa4beBS4H9iCCZA92SA/k54+ZxSxRWIxZoE4C7gIOBNoxqwRETAADCjclc8kdt+6MFNZtyCz8P456eU7M4lZkYgHzMIExG7se+NwnJQ4ceFwHD7FeOodszwNrAaeisV3eEBYCHMPAfcAjwGbskF+7HaOY0RslTgVExBPBi7FMhUy2DUrADuAe4EHb58b9P3T+XNb752TvkBFnoxZMcAsF33A9mP8FhyOaY0TFw5H46nnckkC5wCXYAOSVwhze4C7sAFsA+ZScdaNo0B4fc4HlmNujadhlokWzPo0iAmEnwB/BDbdNzu97fnP6ejAhMdfYbEVESPBwH3H+j04HCcSTlw4HMeGEpaJ0lOzrAl4LvC8+P9hIczdBfwBeAR4womNwye8PjcPOB94ejy1YWKiapX4L0aE3a4lL1uRwATgs4DnYC4RwVkmHFNARG4AXhP/d5uqLjt+Z3P8ceLC4Th+DMVTlSTwFGwgjIChQpi7A7gNeCAb5Pce+1M8cYitEysx69BzgWVY6ucgllr8LaxS7SPB2vw+gPbONR5wNvAKTFCksVibHpx1wnEIqOrVwNUisvU4n8q0wImLk4f5mD95JlE1U1fiqYzFQNQWzjqRKGG1NqqkMBP+FZgbZQfwG+BO4OFskJ8s22XGE16fS2OujqcDzwfmYLVMeoHfA78C7gO2B2tHrEDtnWuWYZ/rCzGLhmKp2t3H8PQdjhmLExcnD/OwG+9Mol4RLZ/RRbSKmHVgOP67BKOq95TiqVjz+nShiBU/q5IBrgT+GqgUwtydwDrg3pPJqhFenwuwgNk/AZ6Jfa/LmDD4GiYqHgzWjq5D0t65JgAuwz6/M7DvRy9Wt8ThcDQQJy5OHh7m5CmilcBcDEnMzN2EiQ6NX2vGBMd+zP9ejtfNYGb0qjghXl5ipD7BMMevfPhgPIG9n4uwjBQKYW4z8FPM7D/jYjXC63MpTFA8J57mYOIrD9yAxak8Fqw9uKJqe+ea5ZhV4wWMBHDuOCYn7jgqiEgGeDXwEix1eD5W4O7HwAdUdU/NuldjorPKBcDrgRdhD13bgC8C/6yqGm9zDfDBmm2WAB/HBG0bFqfzKVX9v4d43pcC/4D9bjNYfZxvAter6oyyRE4LcVHn4i9X1a3H52wcM4ByPA1NsE5VdLRjVo8KZvnoBDbG8754Px1YtkAOWMhIWfFEzXEG4ZjWM64wWizOA94KvAXYXQhzPwV+B2w8UYVGXHtiJXZDfxFWUbWEBVd+BfgtsLXW3VEljqW4GLgKC+pUzOU0nSxTjsPnLGJBAFyNWaBWA58Hfi8iF6pqH4Cq3gDcUBNw+S3gS/E+AuD9wKexGJ13xNtcA1wjIuuAZwA/BD4JvBG7Z3wauFFE5qrqZ6ZywiJyJfAN4OfAhVgtlBdh3+U1IvJcVT3RXLnjIrFQmxbUXHwnLg6DQpgbrymXB/yCk8dycbgIJjiymHCoxnQ8wEgGx2bsqXlRPJ2GDYCnYjeqSrxtESu6NMSxt3RksKcrsGv+I+BWYPOJIDTC63PzsYyNq7AnRsGEwbew97GpnqAAaO9ck8FcJa/ChGCIuUum/fs+mbjkvqEr/+vN2+sNpBLk8/VasY9eSeQszHLwvDHLz8dibP5OVa8f89oN2Phyo6q+pma5YHFMFwNPVtU7a15bh4mLD6nqB2uWp7F7wVzgNFXN17y2FaA2W0REFmIPLRFwiqr21rz2IUzgvEFV/32y936iMC0sFw7HNEEZ7XoA+42cDTyJkaDR27FB7q5skP8RQCE80LSqAzgFS2k8G7N2VBhpmFbg6AuO2vfQhN1QX4NZNG4BfpMN8tMqtTIuanUxVlPiqZjA6wK+g7l7HgrW5ivjbd/euaYV+AvglZi42o9LH52xqOojjKRw1/JgPL8MuL7O6wA3jdmXish/Yt+/V2NCY7JthkXkZsxSeCXwqUlO+dWYO/ZrtcIi5juYuLgacOLC4ThJKDO6PkWCkXRRCmEujxVfuh2zDHRjZb//O349jQmOU7GshtWY4ChjgmMI6OfouVRq010zwBuANxTC3OPALcBt2SDfM97GR5vw+twibJC4CnPtDGGFrG4C7gjW5idybdHeuWYO8GIsSDOFCZLj9n4cxw4RuRx4D+b2WoL9nqrMnmDTJ+os2xDPL6jz2uFuU8sl8fy+Oq91xvMLRcSbKa6R6SouUiLyYcy0uQi7sP8GfLr6wYtIO6b0XoCV8J2NXaT/h5mwDjSPin1d367Z/xnAa7GnuXas8dS7VfWXtSchIrl4vedjjYuymCnsG8AnVbVUs+57gY/WbN6K+ej+Mt7ubuAdqnrPmGOcGR/jT7ABKIX1pfgy8G86nfxWDjARUJsu2gq8Lp66CmHuZ5hV47FskNc4XXRjPP0coBDmMti1XoXddM7DrruHBYzu5+jEBtRaNBYDfwesLYS53wM/AO7JBvmjHpMQ16NYjQmCp2PWlb2YH/vnwdrJrSrtnWtmY0+ML8UGlb2cePEUHnbdk0SaTBc1kyxrJlEhmSirl6ionyxrIlEmIYoc75NtJKmSHtH7EZGrgP+LWRleAjxUDYiMO9RPtP96jQUH4nlbndeoHU+mus0Yquv8i4j8yzjrBNj9ZEa0BZiu4uIL2JPfeVjg3d9jA/XpWEANWI76J4H3YQP4MGZO/TfgaSJyuapWAFT1O8B3anxunwFuxszWS7CnpB+IyJmqWlWRYDevfwTeDHwfuxk8Oz7GasyES3yMjwEfq/HRfQ2LAn5PfJzvAT8WkdNUdaDmGH+LPbVdjeXkN2FPYp/F/PnvPvSPz3EMKTBys2rCruVVmAviZswFMSozIRvkB4GH4um7hTDnYdaNVZhV5EmYlUEY6V3SaMvG/njyMIFzGVCI3SY/zwb5bQ0+HuH1uSz2+3kjJm6GscHhW8BdwdrJhU3s/vhLrOhVAhMVxzKQ9lCpZiE1YZ91JVHSZCaMmpsHo/TCvWV/XnclOb+rnJjdGxXbeyvFtkKkqaJquqilZFkHUyUteTqzYkYW7CsvPcJdfBD7fbxBVR84xG2zdZY1x/N6DQoRkWwdgTHhNmOoCobXq+p/TGH9E57pKi62q2qtunuXiDwJeIOIfFNVb8Uu1ldV9eM16/1MRN6BCYcXYYKgHptrLnBvHFBzE3bT+uea9fYAH1fVr9Ys+66ILAb+WUQuUtU/jnOM36vqf8V//yFWqx/H0uhurlkvD7xPVW+J/18Aviwiq4B3isinVHX3OMdwTC/GuiDeCLypEOY2YOLyd7GwGEU2yEdYOtw24Kdx/MYpmNi4HBv8E9jgVMDcKI0abCJGammksUH7qkKYW4/9Jm7PBvkj6u4Zuz5eBLwcC4btwnzL/x2snZqIae9c0xTv4zXYE950s1SMDQauxtkUmgei7eevD8Mrbh+cvWpTccni3eX0/K5yoa0/6vf0wHfmeKY4Hw+ecoTbL4vnj9cuFJGmKWx7Cibsa1kZz++dYJtHDnGbWu7ArGzL6r0oImcAi1V13RT2dUIwXcXFTeMsuwwLjLk1dmH8ss56tQE944mLW8b8f308P712oareOM72tccYT1xM9Rgfm+AYCaxx0g/GWccxfal1QeSw3PbhQpj7MZbWtmm8zI14ea3YSGBuudXAGsytBzaA9dC4QXaYkYJSS4FrsH4ntwA/ygb5en7nusRppKsYKasdYAGWnwR+Faw9WGTVo71zjY9ZKf8Wa2e+j+lRRTPBSBfVahpzHviDF+mDr/9OL1d/b/+SU3aWL8PcttXMo16sHoPjyHgCs+yehw3cVS6fwrZXYvUwgAPZIi/DxN3XJ9jmAzXbpLHqrsNYQOZk3IhZW64SkWtU9YC1TUR84D+xjsnrprCvE4LpKi6mFDwjIn8OvBO7iS1itJ9tooCesQV0quauUeWxRcTDbo5vwkTB/DHbNeIYaaygy2swP/zYKpoTHcNxYtAbT0ksRuhFwKZCmPsGFlBZnGjjbJAvY3E4jwLfLoS5Vux38HTsZprGvvs9TFzb43DOOYXdeP+6EObuxUT+XdmgfuZGLCouwgJHL4oX34W5Ce+eKOOjlvbONYIF6r0T+130cHyzPzzMH97MSLn5+7FA3keAzdsv3TgPE39/g/2OXdOzo8dngM8B/y4ir8MsEU/C6ldMxiIR+Vus+FoaG/QvAj6jqnePs81qEXk5ZnVuj4+/GHinqk56fVV1j4i8Fov9+4GIvA+zuiwDPozd5z84/h5OPKaruJg0eEZE/h74J0yBPgd4XFVLIrIM2MLEAT1jb8DVJ8ix23wJG/hvwIJLt6lqJCJrgF9PdAxVnfQYsWL+ARbM+THsx7IjTo26Grshz6hArpOcEiNPrQuxm0l/Icx9G/hxNshPKZArG+T7sKDRWwvhgWZdl2LNuqoiu4/6v6NDpYhZMwQrOvQxoLsQ5r4D/DLOjqkGaV4GvA2zrITYd/ubwdr8xkM5YHvnmiXxfi7Dfvf5ibc4agTYTb/6230A+90/BGzt6lhXCXO5ZkxQrMWsS66k+DFAVT8vIl3Y5/4r7HO/G3sQ/DnwjDiw87VxEa1a3oJZwB9kJGHgXcB4gZZgD5kfxYKO52APu69S1W9UVxjTFbUaWPr1uKEZqvo9EdmGWTH/B3vQrGabvX0qIuVEYrqKiwkDbkQkhQV5RsArVbXhqWcisgQTFnuwoKGj4d+9FBMW96rq+47C/h3Tl2pAZYA95b+uEOZ+BNyUDfJTHkxjC8LDwMOFMPcV7EnoKcCfYX5iYaTM+ZFQbewFdlN8C/DmwmDut94ddIrwIlE6sHiQrwP/OZWsj1ri3h9/jd2gFXviP9ZxCM2MNDLrAb5L3Em1q2PdgQeGMJdbHJJ7IRZ8XW3jPqMGh+lONVC/zkuTPZCVVPX9WG2JqR6rHxO8b5tgnauxwPyJ9nMXZrmc8UxXcTFZwM1c7Cawp46wmEpAz1SoRjNvrSMsGnWMZfH88TqvNeoYjulNiLnQfODPgRcUwtwvgW9mg/zmQ9lRHKuxJZ6+XQhzOezp/y+wuA+wp+opxTtMwCARQxRYSMhbouUE5BiSbr5Pheubn5qv930el9gF8hQsNXYuJuiPZbBmBovnALM4fB9rfrapq2PdAXET5nKCFUd7BZaZFuFKijscdZmu4mJUwE3My+L5DdgPegiYJyILVbU2QGoqAT1ToZqSukJEmsa4ORp1jGpsyTkiImNqWjTqGI4Tgwo2sHmYmf3ZhTB3G3BjNsg/ejg7jC0gNxXC3H9i4uLpWBDaoniVbiwgbeooQj/zpYeziAgQStrCg8ylWztYCfx7Iczdhfmm756sLXx755qFmEn6Uo5tVc0kJmTAPoevYK6mJ2oFBRwQFWdjlswLMFfRDk6u7A6H45CYruJitYi8HRMSVRfIZcAXVfU2ABH5PPak8x0ReQsWWf8sLA7jiFHVThH5HpY+dKOIvAczC78YCzJrBL/H8vwvAf5VRK7DbvavxQSW4+QjwhoaCXH9iVhkfCUb5Dcdzg5ji0Yn8M1CmPsWFhPxbKwyZrVdeRcjnWAPRoEB5ko3Z1GhGaGobTxKK50kDtSZ2B+f93lYKeXhQpj7IeYTf7Q2OybOAnkB5l7xODYuEMEsFE2YxehmrOfO+rGCokqYy52FFUi7CPttOtfHCUadxphbRGRbbe+POttcQ02AZRw/8RtVXXN0znLmMS0al9W5+OdjfugXYyWBn8CCK2srdPpY8M6bsJSkYawL5NcxP2mVK+L5r8cc9jequqam6FUtV6jqOhEJsCJWr8TcJH1YIM6vsAqaVZZjT5tfG7Ofr6vq1XEjm7FFY5ar6lYRacNS/l6APV3uw6w2m6ip+Kk6eUU717hsRiJYlpKPffe+lg3ynRNvMjUKYS6JPYm/ALOUCRY70HdgJeu2Mkd6WEmJtthSsZk2nqgRFeORYiRrogtLz163dO+KFFZcbhVWr+Jot5pOMdL99mEs7e/2ro514x43zOWWYMLncsxSsQ9nqWgkV1JfzE6pcZlj+jMtxIWjMThxMaPxMKHtY9Vrb8gG+YZdz0KYm4W5Tf4SWIYSMUhZelhBiVkIZc2ylTa2kWTC1NlxyETK7N2RP/+BcjDr18XM7j+UmjZvraSOqEDXJLTE0xBmpfhJV8e6CWt1xNkfL8fiKhSL/3A3ycbjxMUMx4mLGYQTFycFHrAAc2XcAHz/SCto1jJwa06kyF9qlvfpAs7AJyLJdrI8SpLDPk5v5GXXl9NnDynZWV5UzhAlEGFnJVH4VTGz/belzL4GCQ3BrBQpLIblRmBdbaZHPcJczsPcqm/HBMkepndZ8RMdJy5mOE5czCCcuDipSGEBib1YH5p14xW2mgrh9bkElgFRrVMxqE3cUnkBW5nLn2Guv2rTtikfJ1JkcyV5SmcluUKEKInWuCKUjGgyIEqICHsq/sDvSpmdt5Wauh4upwuH2Kur1rJzD9bX596ujnWTdpgMc7kORrprdnPk2TSOyXHiYobjxMUMwomLk5JmrNDTeuD6bJB/7FA2Dq/PBcAzgXdgWST9WBXOm4K1+d0Aca+TM7Huk8/Gvk+TVgPti7zMI+XU2YPqtaVEQ5koYBSlCU1kPE0qUIi84TtKwe7bS5l9d5eC/UN4423rYTEpHlY6+RtdHeumVLQrzOUSmBvoDYy4QI41AqQUmob9dFvoB5kwESSH/XSq5CXTZS+RjsRL6QwqpidAWfxZ53U9VE+kOnExQ3DiYgbhxMVJzVzMmnEL8NVskJ+wU2N4fW4WVmjr9dgTfzcWDH1LsHb8WI5CmJuDFX67Esu8KGLfqwPfO1XojBKLNlVSqwR0tLViaqSI/KxoSm13PFpO7ftdKbPnrlJTbz5KhIpU3UMAPwW+PVk8RS1hLnca1lH5DExUHE4cyeHQBGQVUgOJTHog2dy6u3mhv7nt1NTW1mXFztaO4a6gvTKYzAz3J1uGCqnsUH+qZagi/mFbpaYj5+594KXf+skrneViBuPExQzCiYuTnuqAO4S5Sn4Wd1w9QHh9bin2tP4SrBLlHuCLwE+DtfkpV/GMy45fFO/nUuKKlsMqpUfKqVU9kb8gKTrsHYILZfw3pZKVKJUUPED2RL7eVWra31lJ/GRAvX/59oK7p1xsLMzlfCy9/E2MCKOjSRKzLPkKXncwO7xn/kXhz5b96YL17avY0rq8WEykBzCL0UkT43Hxrruu/M6PXu7ExQzGiYsZxCTi4jbMPz9TUKwyYokJze0nJU1YUOMDwCcTnycPXAhchcVVpICNWHr3b4O1Exe6moxCmJsPPKcn8v7XzkrivJJKYhDpi5CG3lyKKoGistCrdC33S71Nng5jVvbHse/3/cCGem3tAcJcbi5WM+dirJbI0aqs2YRZdRQY3he03/Pl897g37ziRau7m9pT8To9cPgBsic6TlzMfKZrES1H41nFzBqEBRNNgt3EK9hgMRRPw9iTYDn+u3aaSZ9DPYaAPBXOJuSHlfNQ72GQCiHwW+AbwH3B2vot3w+VpXtXdAHio4knJYce/Yt0ofXCZLhAUBlWrzygUjqSkIEykqooiTYv2nuaX9w4y4sGal4WrAnc1dh1lUKY24T1A3kIExvdYS73ZKxldsDRaYSWZKSWRneE3PCFC97S9fkL3vrkkp96WrxOF0e/pofDMS1w4uLkoYeZd2MrYabtqoiIsO90On49hTXBK2LFoTLxa9Vt/HibIaz75olvllYgpJV+cjLIYoW0rkQrK3lMunhv8wX5/2nk4do718zGujw+uYLsvL2UKd9eyjBbKhuenSrMe256IJfzy60oDKiUQqQ8VaFRgURZJdUk2r8iWdwwz6vUs7wp5lLoj/8vmGvoKiAiIlF4INci72WWbGC3bGEfG/BkqGECcxb2vQqBH5Qk8fPVr743Gyaa3sxIhs0upi5oA8zykcK+y1E8zSQTsyQrpQr2cDCW/jrLHCcgzi0yg5jELbKVmSUuJJ4S8ZSMJytUbWKihKUVDmGfQVVMeJgpfWv8/0VYYF863t6P99FPA2IGjgllkhRYIH2cSoUMAAn6tY1NNLMXn1ZsEPwm8PXJen5MhfbONecAHwFaGWklfxDL/WLTs1MD85+VGsjNlihAlP7ILxaRup+tgldUSSdEi6f6pccWe+U9nhzG4DpEmoc4lyJzmEUZHyFC8RD2MCAb6ZVH2S9bGOBxBqQw5WtdzVDxgUexz/T2FX+z8TSsquf52PdvMjekDweuSyX+/25gM1ZmfAdm7ejl2AWcHisG89cGW4/3STiOHk5czCBcQCdgT32zsUJICezGncSeIPcz4jIBu5mD3dB/gpWGTgKnA6uxDphePA1jZbGnTwfMCGGQORRYIiELiEjiUdQM22lhOwF9Y4wEPuZC6AQ+dKhpq1XiLqYvxWpiFLDPdVIE5bzEcMszUwPzL08NLm4WTYJKoUZoFFUCgCV+acupfmlbQg7TwtBNqzzC+VRIji3+pQKkSRCQGCU49jMsefrZSK9sY1C2Mcg2hmqsHAkss0aBX2LdUx9b8Tcbc1g669Ox78m+Cc4sgZVErwrd+4C7gQ3Apvy1wZQ+S4djuuPExQzCiYtxqQbYNWF1IUqY1aMfu8FXnxrB/PE/wGIT9mKm7ZVYS/CLMHO1hw2q/Rxrc3XV7VFgoQzSQUQKiEjSp61sia0Ukz2Bz8HM718DvpUN8lMWTO2dazJYwalnYdaKwxJbHsr5ieHWK2KhkUaDCPE9dO8yv/hQ1jvMYEcFnmCxbGEVPmX8qZ2fAqTwSeOTJkElFhQeQh8leQKlkwIev9RLuZkn8fh373tZ7/t/ct0LsUaDE5UKr1YNrYrc32Li5N78tcGEtUIcjhMVJy5mEE5cTAnBTNFZTGx0xcsy2GdXjcUA+CPW5OrubJCvxOmXp2GZF2sw0VHdppuj5UJRYJgsg8yTAqdQoQkQPIY1y1ay7CbFwCHGTCYwK8bjwDVTaYbW3rlmCXAd1oRvJ40RVgkPXXBuYnjwvc1dd12aHDpT5ED9igHMWjS141QQHuVM2UOOFCGHa/UYQbRIQApYxB6W0EPKrndhuLl5Z9+iZX1ha7J/uLWve3DOwN7CvMHd/QvD7sH2YvfgnGLP4Jyoa3BOW1/YFpWj5N3Yd+m+/LXBTHJPOhx1ceJiBuHExSEjmAslwCwYG7BgwGonz+pn2QV8G/hlNsgf8KMXwlwL5j55FnAZI6bubo7UfWKCorlGUGRQPDyGNcNOsuygif0cTizCaOZh7/VTWF2Muvtr71xzMfBh7D1OZPY/1GMnsB4p3+nqWDccVwPtwNrNP5vRAq6X8T7XIgke5Fzpo500Qxyp8CkRoIjOp5PlbKPJXGmlSsLftG/F8t2FBUs9qVTS/nAp6Zf8pF/yEl7Z8ySSSpSQUpRMCpHOzvR0tTd3dTclw574/Pswi1dvPO3HRFQRc6mEjAQoV2rmMy3DaTAb5Lce75NwHD2cuJhBOHFxRKQx07VivSl6MMHQVLNOGfOzfzcb5EcNsIUwl8YC+a7AxEYKGzC6merAoAhDtDLIPBkkR4UgFhRFbWIXzewkQw9ewweaABvo/wcrIX6g5Xp75xoP+Gus6NR+zB10pKTj4z0CfLyrY92W8VYshLk27HN9Otb+vOqWGrFqDJKWB1hNSDOpiUuST0qFJGWS2sY+VvAYrSN9RvYPtTav333W+cPldFMqUQwZ81tTFSlFycCTqLKkbfvmXFvnjlSiVM1AStSZ/Hjy4n1Vs0LG/oZn2k1asOtZN1skG+RnHePJ4i6kAAAgAElEQVTzcRwFnLiYQThx0RBqMwHuxApRXYG5Q6rWjDJWZvumbGD9N2qJhcZFwPOx6pXVwfDgYL0ySYaYxSDzJWRhHEMBHkUN2EUzu8nQfRQExVgEy5rpBj6QDfIPtXeuacOKTj2VI4ivGMMCbBD9LPCjro51U3Yl1bilVmNuqVUMkGYbKygAZQYOu5qG4lEiTYohPY1HmU931c2kCvnejkVbupevElQTfnmsW0OKlVQgqC5o2bVt2Zyt29KJ4omf1nx0GbdxWTZwRbRmAk5czCCcuGgowojI+AVwK9bg6wpGP2neAtyYDfLd9XZSCHOt2OD8MuA0IiKGGWaIFhliISVaiUgiRHGmR54Me2miF++4PLG2Adk7S8Etf9275PIImY3FVxwpVevIncAnujrWHSTKDpWhZ+cu09l8Ws8no5fQzAKaURRBGKRESHlKNUJLBADaweMsJY8/8rmXKgn/0T0rz+wamLs46ZeGPYlGiaFylEhFkefPbd63Y3n75s2Z1JCLp5gaTlzMcJy4mEFMIi7WMfPKf1f90UeTqiVDgJsxofEirHlX1awbAl8Fbs4G+VFZDnEr82UqnMMC/iI6hWdojgUIQiXubZFhF030kKZwvHtfqsK2SmLpgHpnP1hO7/v4wNx7utU/0qfw+dj1+hfMWnHEN50wl3sa8CHMNTIAoLNI6AW06rnM0nOYyxKyKJbxUaTCEGXKRAc+4gifEmltoZuVrCc72qXSH7ZkHt519vnDlXQm5RdHvaYqXqmSTKeTwwNnztvwyOxMTx+OQ8GJixmOExcziEKY68XqO4wlBH50jE/naFPN+mhidMBbAguMqxbPatQX3MdM+gXg01jw51XA8+LXFNjHAP/mf4NdUmYl5hJZHZ9nKt52lzZxa3QZFV3BU/FZEJ/vqM6ix4NQJflIObWqN/LnJyUK50qU6leveN3A3AfuLQeHM3imMGHxAPDRro512xtynrncc7GOpt1M0PZdM3icRUu0ilbOZbYuZxYZkkQoESmGqTCfR1lC51hRt2+gfdb63WddgCJj3SClSjKtiLekbfum5XM2P+F70UwLtjwWOHExw3HiwnFCUwhzKWzwbsOyPDqAs4AzgRzEz64mNvo48qj7THyce+nmc97jLI6W81YCLqZECxVS0k3Ju5su2U8PVvvgd5g74OFgbX5vzbkLJj6uwmI0qrUSjnlV0L2RP2t9OXVuRSWVEj0wYGclSqVE/RuH2h79dti6XaduWpmDBW5+HvivQ4mtGI8wlxOso+s7sM/pkFwQaoXBW/RUOvQp5PWVPEErS7HaJxVMmBZ39S1ofmzfGad5aMn3KgesNqoipUqqKZMa2H/m/EcfaQ36B8Y5lGNynLiY4Thx4ZixFMJcEiuCdS4WnX5uzctT77ViDpiAIk2UaGaYNjwWEBHIBnrlYQZlPhKtZrbOQkkxQIL9lPkqWf5jKqW2C2FuKVb18vmYVWYvx6DXSUWRxyupU3dUEst80XKiTtBmEvVmeZXgd8VM/hMD7Y8N4U0k0DwsMLQTuKarY93GRpxnLCxeDbyOww8urRay+ixwS5DPR7HAmw0sU2XprZuecVUpSj5tcet28SSKFMGXSEqVhDdUapI5ma4ty9q3bjyscuSOWpy4mOE4ceE4aYizOFZhKY1/hlkhIqALpUKZFGXSlAliMdEqJVook0FJoHFxLSFCKGuSAVqIqLDB28B1DHBX9CzWAG/HKoJGWI+Ij2WD/H1TPMd5wF8BL8GepPdxlPpK9EVe5pFy6pxB9VpSoqFM4JYRlHYvanqikuj7YGHeA9ujZD3B1IxZLP4L+GJXx7qGVJ+MhcXfAK/BgksPVXRVBU8e+ECQz28au0Lug2EKqzz6p8BO3ytXOto6g1Nmb2uanelZdGr7xsTzz/rhA7lZ25uxa1sVNz4mBqt1Korx5FwlE+PExQzHiQvHjCW8PmddJCwOpXaapUkW6VJWa47VOo/TgBTDqJSxtESrOlFBqOATapJ+UvSRpECKAVIM1RSwmocNYJ8Gfoy5aN6IWSF8zOT+X8CXskF+SgNuIczNBl4IvAKLXdhLg/qaqMLWSjK3NUqeIaBJdIruBWWWRMEwUv7owNz77yw11abWzscG1X/q6lh3WyPOEw4Ii/+FtVTfwaG7jKpZKjcDXwjyB3/+uQ+GaSw49FJMDFavq4+JkvuAD+WvDfbBAZE6N97vvHidJcBi7HOYy0hBteq+ahvnjS2QVY0Zqs5PBmHixMUMx4mLGUR4/bgBnYPAPx3j0znaCDbopjFTd/XvLPZk2cxIkaJqx9Rq4SKwG3kRKGqSUnQaqmczj2YSePQDe0kyRIJwiimh1UHsd8AnskG+pxDmLgDei8WBCLANuDYb5B8du3EshGAkA8UDpPJ8ZukS/hKfvwJ8lH1AJT6j6jaCjvqbusuBIZVgYyV5+oB6bSm06MU3eAFQkJp+6HEap0jtwRQJvMhPeSRu29vUeefeoLvkeXPailHnazbt//aq/cX9jDR7q538CebC6IJSXnzuPlt4Ej1cRJL+A31wJT4d+zfyNwdelzgbJwB85vNH5rCzZusDU0kTyXsqF17Ury3taQkHBRUrZiJ+WRPBYm/HlhXexq3eSE5rbeGn2s/2wJkpVBujJUmT1DQJ0iRIkdS0LSNNkhRJEvjqY/8S+Hh4ePF+Z/ateQ7z6gpFJy5mCE5czCDC6ydMRe05xqdzrKitaKg1U1U8lBgxWVfN1uWaZaV4XU8FtIM5upJTdDazUSJCimNCGGtv/KNeUhAC0pQo+7fxuOxlQBN40bks1tNZjIdHBZUN7PAeYq9EB/YhY/Z1UIVGzZCIzma+LmNu3Lxs7HlN+ENWe8PpIbyMHVRNVMRlwZSRCmFTCtn0FD/AH9jjV6J7Nb9of7SjZtSVMfOx12iyuaJAP4sosBif4QOv13+XB79WIY1HkTk8SsDAqPXiv0ua8NdXVq4a1ExrUkrhyKZ+oqJ+Yqm/bcNib9feOked6LOu99pkN9mDXlfBUmhrxcbMQaK5vFBfdHiWCxG5Gmu6V2W5qm5t4Pk5GoATFzOIScTFHVi2xExibMnk8UzKhzoYoHNpjs5nmc5lDhEVhg8azMfdlyZJkiAh97He28AuAXQhLZWncDZN2ODeS693Gw9J36GVq9Y2gugCTtNFLKwW5JrsvMrg9+O1lpC0h473HTkkIsQXVNuCKEwO0+//ngdkD/1Hul/Azq6bZexnBYlDTicWyjQR0MV8HiJR35VU1GTivsoFqwc105qSkRoWZRJpQFd56++b5+2bSXVhphXRIq6MXnJkbhERuQGLw3HiYhrixMUMYhJx4Sp0Hga6iLboAk7XNmZRpiSlKbbw9vBIE8gTdHp38riUiTSFH13C6ZojZx1DKHp38oD3BHWre064/wW0Rqs5XWcxmxIlKR98XgoMIpkBvBaAWFgcMRHi+2i5jag3ARVNksLHk4fY4D3M9iN+zO6hgx7OPGRhofhUSNPKFtrZPF5Tt6ImE/dWVl84pE0ttcKiqKkgKaXhc/0H722V/sF62zoagxMXMx8nLmYQTlwcHRTQpcyJzudMMmQYZliiyYPuFKCJJumjz7uVB6Rgqa/RMuZGF3M2KdJERPI4m7x72Cp6aBYFBXQ5c6PzOZM0AcWR8yopyX7xWsuQ9KBSDRmYaOCv6/4Z9WYgAj+NDjerFqTG6aEeHk2kZBe93h1sk5AyB7tHZJxlI/NBZtPPKfgUGbFITSYx9EA2T5ZtNB8k1g5sXVHP2xSdumJIm7IpSsNgLoiSJtOBhAPLva0bU1KqJ8ImOoNxP1YFyoJfFvyKJ35FxK8IfkXwIxHP/hY/srkXga+Cp4Io8SQy1m12wpPKRouWvqh8RDEXTlxMb5y4mEFMIi62cwzqJhxjal0h1TiLMqMj76vR+NXYion2NfHBPLxoFfN0FUuAenEP9XcakKJI2b+Vx6WXEBBtJhldxnKdYwG4spf93u/ZJkOjrtHY3Uu9v9XHi1bSrqtYqEAY4hfxAkBFNAIZ+ZXLgRH7wCKNo0h01P/jbcSWR+BF4LUS9WRFrRvpiGWg+reSppkKoXcXP/c2kWd0BsTYa6I18zKbOI3NvAKPfoRiTfTF6HntEtuDlfk+jS9zFhsZ7SqrnmO0X1u99w99+A09OvvclBT3AETq6TDp+c0y8Pj70h/9l1P9LVVLxnixPApQEri3PWh+aFZ61s5MYnZPymvtT3qz+pL+/NCXuUVP2suetFSEbM37rO5Q4s+5Wtk1AiKFSEZ/nxWtXp4ZFd4pHc2lZ/7H4l2NslycCbwqnhYBTwD/BnxatRpbJO1YxtEL4vVnY7VY/h/wIVUt1Oz3SuDbNYc6A3htfKx2YD3wblX95ZjzycXrPR9YgQWXbwa+AXxSVUs1674X+GjN5q3AJ7EicVngbuAdqnrPmGOcGR/jT4BTsUD2R4EvA/+m02hAn7biQkReA7wZOCde9CDwRVW9sWadpwB/qNnsmVihpDdj3ROTwNdV9epDuSgi8iUslRAswv8pwD9jOfAprInVW1V1c53zfiqWmXEJNtDdCfwD8AngGfFqv1HVNTXbnAV8ID7/NuxL/33gOlU9uJPmOEwiLh6gMe2ypxMW9jYSwV/NPDhoMKh5bQDrsbIX2B1PvVg9iS7sM6o3sFTR6FzmRqt5NQEXErEfpdaEXlvEcmQ7jzZApZN/8n/CI4BqO37lL7iKgJcASZQd0sk1/o/ZNOa4owecg2NN9I2XLqDnVP+vnpcufGR1IpxXRAYH1WtIfYwiEnho5axE8f55XmUqcQitWNbSN4AbskF+UldSmMudh/3G+oBDcUkswIKV/y7I57eOt1Lug6GPdXh9DlbvosoS4B7g7/PXBqPiX9o71/hYaunC+DinYPeVjvj/1TRjGF3vohpIXMLuAdPzJnsceVJi6Mrvzd7eKHHxK+C/sSDPNHad3wl8WVXfGK/7UuA/sbLxX8GCuZ+KiZCdwOWqo92GNfv/EZbK/D3s+3ITNoacqaqdNev/HXbvfzN2//aAZ8fH+JWq/lWd97AOGxe+D3wzfi9nx8fygdNUdaBm/c9hFX2vjtdtAl6MFYb7V1V991Q+u2PBtBQXIvJF4E3APwJfiBe/Ffgw8DlV/dsx618DfBAz/d+HNUgS4GfAXbG4OOSLIiJbMTHxIPAxTE1ejn25tqnquWPWXxMfc318nPXAxcAXsfTIDlWVMds8A/vyPoKJn41Y580bsS/9U2u/XBPh3CJTIsFI2mqakQFC479DbPDZjInPTuxJaG+wNn/gZhhXdrwUSzVtwapGTvZjasFSZK/NBvnf1OzracD7sQJUvcD7s0H+D/V3cTDtnWvOANZiBcK6n5YcTL8l071qjldp6o38sMKUeoMehIIUVYKMRP3nJocfaBYNJ9/qANUaEY8DH8kG+S3jrRjmciuwMuFFOKSg0MXx/t8b5PPjfrdzHwwFKxn+EkbqWAg2UPyhvPzWD5WedV07Jho6gJXYk+cSRgRc1coQxtMwJ0c9iqNCg8XFjar6mjGv/Q64DHiGqt4qIs8GrlTV141Z74WYcHipqn5/nP1/VlXfXrP8ZdgY8C5V/eea5a8GVqjqB8bs5x2YcL5YVf845rV1mLhYq6qfrln+HuDjwItV9eaa5e8FelX1S2P28xngbUBOVY+443AjSBzvExhLfLHfBHxbVWtrM3xERM4G3iYiP1PVH9bbXFXfU7Ov67CnKLAB432qekv8/wLwZRFZBbxTRD41zkVZBLxNVX8d//8nIvIN4M0icoGq3hcfywP+A/tMX6aqj8Xr3yYia4Gf13mvAfAtTOhcpaqPxy/9NP4SfQVT4f9Q98NyHA7leBrv6TiBPa0uxSxV1diBKLw+txm4H1ifMPFxZ/mtvBr4O6y8+D5s4BmPfuxp9sOFMPd54D+zQV6zQf63hTD3N5iZ9EzgE/HrN2WD/LjCoL1zzXysHPafYoNdHuC3pczg3fuD21+X6Vn6/PTAqWUl6lNv+FDc9hXwyyrpBX75iZV+caMvhzyQVuLzyQFfKYS5LwHfzwb5UU+HYS63ECs+FjF1YSGYsLgH+Icgn5/M0nE1Zm7erslBL5qzJavZ3Uujxffuqpz+q4V40Q8ZbeGqNr6bimB0HH9uGmfZZVjJ+FtjF8Yv66z3YDy/DLMe1OOWMf9fH89Pr11Ya1Wf4Bh/HGedqR7jYxMcIwE8GfjBOOscU6aduMCEBYz2eVGz7ErgLUA9cfHd2v+o6jdr/j7cixJhJrdaai98tazzZZjJ9I81wqJ67F+IyF6syFItL8Bukr+uERZVbsLExdU4cXEsKWPCc6wLqVpCegUjrhcSn2eDCndGz2aPnsaL8SljLpfxCDFXzNuAlkKY+0osMDoLYe5NwDXA07An7WWFMPfpbJAf5d5o71zTjJUIf1V8XjsZ8xQ9hBd9drB9y6+K2T3/O9N11il+qW1/5IclZFKRUELSACsTxfsX++WJ3stU6MIsRW8D1hTC3HXZIJ8HCHO5VuBTmLie6nGqFodbgQ8H+fH7trR3rkkmf7P2Kk5Nro3mPxLpnG0dGvQ2UUmnSBX6tGXHbjxmYdfDWSFOXJ6os2xDPL+gukBE/hxzl6zCfsu1anv2BPvfMeb/1XtDpnZh/ID5CmwMOx17SKmlEcdIA6/HLCqnYtbOqR7jmDIdxcWT4vlBVQxrlj2pzmtgJuy6HMFF2VcbiBNT78KvjucbqE8nB4uLS+L5QX0nVHVARLqBxSKySFV3jrNfx7Gh+mRd+3TtAR2irPJ/QaR3EESXMV/nshxhG030kKjbF6SE3UxeA6QKYe6LscAoFMLcezHxfCVmxl9cCHP/kA3y/e2da5KYleKNmEVuD5OUBH+knB54U9+iu18e7F/88qDvDIDecawYVTdIk2jhnMTwAy1e1JDeIJi7I4/dcG8ohLnPe3/LTzwrub0EE0dTwYvX/wnwySA/OpajvXNNK+bSOBu4hGLmwvJZt5yOV6mgUqacLjMwD0kO7o5adt2Hd9wERbUyabVirIeq71VIpkpR2q9I0o/U91R9LyIhiieH0I72BEBoopHDYL1YsqoruQ1ARP4ei4f4MRZ387iqlkRkGbCFic16Y38HVWvW2G2+hI0xN2DCf5uqRrG7/NcTHUNVJz2GWNbQD7C4wY8BnwN2qKrWFBabNt+T6Sgu2uJ5vTiD6rJZ42xb92Z4hBel3j7rfbmq7pfx4iPqmXyr7/VdIvKucbYDCx5z4mL6EWEBiH0A0gfez9kdXcgqXc5F9FISYUAD9tBEN0301gxoFcz//3JMYPxrNshH2SBfLoS5z2KBxP8buCxSPvu8XU++GZpeiQnUnnjbKVFG9P+Gs7b/rpTp/j/NXWed6hdnj7ViVCBRVkkt8MtPnOkXNyYO3Q0yFfYCaZR3Ra/mfbIJ5DGm2jXVx6x83wM+F+TzlfbONXOwp9DVWNB1DrsmPqVUSfackRO8IaRiIiRKBiTCvmjehvvxoka+v2op+moZ+hR2b61mxxx4D35Zk03D6mUHIp3dV0m091TSbf1RurVQSWcGI9JFraRLWkmW0FQp0lRJ1a8gfkMqlEwfFreWLUquMWTrLGuO5/tFJIW5lyPglara8GrFIrIEExZ7gDfUeSBtBJdiY9i9qvq+o7D/hjIdxUUv1vinuc5r1WWH+uU4FhelmtVR77yhfs+PauT9P6nqPzb+lBzHGqkw6N/FHyu9LNDVnK0VAhlgKQMsBVRT9JBhN030kGQIYTsWD5AqhLnrs0G+EsdZ3NI11LG9oPKFgnoveGum+3l7CvPu21JJTVlUjGVLJTX0tr6F97wi2L/k5UHfGRHofvWGi+oFnmjlrMTwvQv9ytEO+h1mI0l8Tq98mqL8hMj7KltlaEIx4wOLd831b7rk5mV3VHx5PZ1rnsaImAD7/ZlpuZJIeHtXXYImPDyrZUGUDPBLQ9G8DffhVw5nqE5j/WMCTERUs0CsD4rdk3ZhLpYdwK5Z+ytDz711oPXJ9w3NPfux4TMX7S2f3jIQNSfLlBmJ7djHSFn6GSYhxie6mDMbqO5OAR4as2xlPL+XkfFkTx1h0dSgc1gaz7fWERaNOsayeD7Whd7IYzSM6Sgu7gSehz2RjP0QV9Wscygsi+dH86JU85FXjvN6R51ld8TzZfU2EJEO4Czg59Mpf9kxOf7j7NZeBiqXc4E2kyIkFEWkRBu9zKEX8BnSDDvI0E2av0BIFcLcR5fuXSHAZXDa61b6w/qRlr2lZV4p+ZmW3Wd/sDDvnvvLwWGX2S4jemM4K397qan73c1d5y72yu0l0d1nJooPZWSq3VGPgDwLJM9ppOjTEujzWF65lIXeF1jv/X70Q0PFg4dPT7c9sDK1/Dt/3rbn3rPTL0XkJdiAvp961ptIxNt3xrlUkk14JbM6Rok0XqUYzXv0HhKliZ4oPex+kMGsD9UsogTQjWVybYmnauryPqCnq2NdJczlfMz1cyHwZ/HftVlI/Yw8UDgax5WYu6OWl8XzG7BrNATME5GFqrqrZr3LG3QOVZf8ChFpGuPmaNQxqrEl54iIjBkTGnWMhjEdxcUXMHHxcg4OsLwynn/xEPd5LC7K7zHxslpEzqgN6hSR53BwvAVYoGgeeIGIzK6jqr8ANKvqzxp0jo5jiOyl4P+UO6LLOUfbadchBkVqYjAiEtLPafRzmgpFnc3VjxRT5/kaSUW8+UD/o5X0pvf0z99xXXbPhYv9cst12T0XXzcw997bSpkjGqQeq6Qzb+5btO2TLbt//OJ04TwRAuwJ+ujRTats5BySDCOoVIAuhrSZZPSPXKj3sWfga7Lp9wszmd8+qWn+fWcF8yOPTNcsf8/2hYkBRKx41wRIz/LTGW5uxy9aBon6SUSjaN6GP5Icrn1/ASYimhixGCh2r7gDi53KY+7I3V0d6+p+NmEu1wI8PST3DMw1k8JESgGXbXKsWC0ib8eERNUFchlWF+k2ABH5PJbV9R0ReQvmdnwWDeoWraqdIvI94KXAjXEqaRdW7uCdjTgGNsbcicXq/WucDTmMlTC4cqINjwfTtc7FZ7Ho8mqdC8XqXHyEietcXKGq6+rsz8OKbV2CxVvUXpRPYDeD16rqDWO22wqgqsvGLL8ai9MYtY2IPB1LOX0UC9ZbjwWffgKLEzmrTp2Ly7EAtUewDIEHsSjj92BfmDWqev+4H1YNrs7F9ER9JHoqK3UJSwgZGlvmOwIJVZpLkWb9jPhd2/2B7/a2rP+fxc17H56VLqgIC71y6mPZPauX+8XZg+oVPzow995bS5nD8R0nsRiex4APd3Ws21YIc+dgWSrtHK0BcYi0/JFLiPDGNhMLk+J1N0t6cJ7XPJDykj/Zkx26bW9T2Nod+V1zElsfWZF6HJk8Tk3658+XnqXn4ZeGrOCo52vkpXTuY/fT1K+YoChjD1Vd2O/zIcwS8QSwq6tj3aTW+jCXy2L1a/4Mu6cIFljbw8yrgntUiC7myug7DeuKej7wBmwgn4ddyy8xukKnj2VxvAnL6hsGfgd8ndFZhlfE818zmt+o6pqauhS1XKGq6+LSAu8GXom5SfqA/8HqKn25Zv3lwJox7wFGCj5uZcTNcmAbVd0qIm3Yb/UFmFtwH2a12URNxc+x48zxYFqKCwAReRUWNX9evOhB4AtjKnQuw24MY6knFKZ8UWrESi3Xquo1IgcXJKq9kHHV0Ouwp5hhLGVuLaaqL1HVVJ33eiZWROnZWAz1DuA3WIXOx8auPx5OXExfFIguZJmeyQpCQomIyuAPIs0hXhOAh0agGjSRLDwmYd9GP+wKEkM/Xdzc+bNc856BZq/y0eye885JDM8fxCt9fGDOvb8uZg+l6Vk7FjvwH8BNXR3rDgzyhTDXArwLi6Tfy8T1Og6NMh73cJEM0UKSUAWGkuJ3Zf30rla/aTDtJQD8CA2iKGpJRYm+QY/v9rRuvml+y30q3mRHgOFss7dn5ZNVSiWSQx6JYpIomdTs7m009W3F7h/3YvVJtnR1rJty5VuA2OVxPvBCLFXYw37fPbg01kPmSMSF48Rg2oqLmYaIbAFUVU89Wsdw4mL6Uz6TxaXVnDdUkuRw2QZVExU1102UVBOJ3Y/7fQOb/WKmHCVB2NCW6vrF0szOZ50+sPiC9PCCQfVKnxqYc/8vitl9kxy2aq3Yglkr6mZoxFVH/wR7+jKnxZGiwEOcJV0sGshKcV+LH+xuSzQNJcUHSESqicroQUYqJNLN0XA6q+Hj5VTPl4ZmP/ZgORivdL1PxZslvadcQJRI4JVLUljQ7+06R6WS+m7pqV/8DNDV1bHusG50YS43DxP9f4Wlr5exBxMnKI4AJy5mPk5cNBAReRswV1WvGbP8bKy3x+dry8g2Gicupi8DvgT55sSiXU2JjqY5UdOp55ayRFqplOoXtRJRUgGJ7RsS+3u2J4ZElZZSlEpE6peTUilfjrbPrzT3e97wpwfm3P+zYst4AmMeFlD478D3aq0V41EIc8uxUvs5LObgsG8SQ9vktO4+f+XOub4/mPJMUFRUE+N0lZUKfpQmLLfIfkRpkyidAO/2UtOOLw/N2rw9SpawzKssUEGJvPxFWW/bU1u83lO2evtO75dysAgza38of21wyCIgzOUECx6/Equ8ChaIeTTasHtASiFd9JLZYT+dLXnJRNlP+sN+KlWSVLLsJ5I60j/nhEeA5JLiolNu3npEXVEd0xsnLhpI7E75P5hf7wfYU87FWP+SLOYW2XO0jj+JuPgDI+myM4VyzVTbyGtaUBL83U2J9p1NiSV9SW8OQFK16CmVptYouWx1abaqMq7A8JRkGv+JB5I9/fv8A4GgyUi91nI53X5+1Jw6RRM9CX/oY+GcP/6w0lr73QowYXEf8ImujnXjFpirRyHMZbA6G3+K5e5POdhzWCWxO/Ln7RpKnDY8JAvVI0pUNOWzzlkAACAASURBVBpPUBx4vxX8KEWx3Cq9NR1XiVC/TTQbgf5suHnP94dbf7s7SvwKuD/4+vfPl1LzW7HgS8XilTYDb89fGxySayd2fTwFKxm9EoujaJSVwsMCSDNAsiQJHUg2txZS2czuzAIvn12S2pldVN7VvGioNz1LB5MZDf2gGCaC4aFE03BF/JlkKZHcqU888wtvfrOzXMxgnLhoICKyEque+CzsqS+LxU/8EGvre9SEBUwqLo5+muGxZ2zn02q30AoWMzAQT0OMCJBqx8phjkLzqQhkX+DP2tmUWNSV9hcqiAdRMjo4zTNoiRLLV5fmgFIeR2B4voqfwNtyT6prqM8bFSwoRJx6VnlOy+JKU6UilVu2t2z459lzNu1uSsyO39u/Aj+dSpBiPWI3yZ9hUfbV+IK6VBTZE/ntO6PE4v2RPxfFT/dF2UQFZQoFuaSCrwlKpVnSowJlJBWpPa2nRMN2r7J7rlfunSNR4Ash8I0rv/7d9fftWP0pRiqVVgvZvTZ/bTDlsuVhLpfEOhK/DhMngxO91ymSwiwsAVCJQPY1zet6YN55xd/knjH3sdlnzOls6Qj3ZuaVVbzq9/SkCQa9KHfXld981cuduJjBOHExg5hEXNzGzMuxTzLS3TSNpRWmsafDNCYchhm5cVczBULMilOtolip2V8JEyMh1C3dfRBlwduX9mftaUos6E77CyrgC2gy0mGZxJISZKPEstWlOeIp5WJ9geEn1UOFzXenuopDMtqULEru7HJb++JKcxTCznsS4WPF9G3ZcvSBZ+4avDtYO37js6lSCHOnY0HPc7BsEsDyMfrUa94RJRbtiRJLIiUhQpRQLaZ6dbZUSKo3eWEoifArCSpDrTKI2GfQ6kVd87zy7nav0lunG2uqHPkL1u866/RbHnrRjv9++IUb94ezBBMGb89fG0wtuyqXS/x/9s47TpKyzv/vp0J3dZicd3s25xzYBRRkDRgwJwynJ+LhiXrn6YoBPYEz4Z3jqSigmE5/6pk9BSUJK0EJu8vmnKdndnLqVN1dVc/vj6d7Z3bS7sICS1OffdWrdip1dXV1P5/6hs8HVbX/gcK+A4wvJX06ECjF3QjqvktL2LSpYXXr95e8r+nB2MXn20YoXNguUXid5+2Pr08uSh8+uSgh2C2xAcZXAs2hRL7OXgfAuQGBqicARRxyDFtiSxRZiKCeaA3UtdEK2w6ifuSLPg97UK2JIVSr2LTCfm5hGw/1RJsC3IwuAr1BvbLb0usHAnpdIScuDU/mtDOMhgTDnj5jVb5a06WYiGAYQak7WeEe2hjodfMndyxJTepTlzrVdQ2uYeZkIng/+0U3OZSD60+Ap0wyknasEtVttSon6erwjOp215iWllqZAAwhs8X3rSdlmZ4hLPXJiYWrIRwhDARSRumrMdzjtcLtrtHcgcnkx6WE7ceXLUnlwk014V4v5wa8P+x4/dDDhy++8a//unR0e98YFNIfLwKuRhW6DvLkSIWOIlxFvaCdwP1/m3Lh/ite8aO5nqa/ERXBlKhISKl9/540fHJR+vDJxfMAdkusCfUjV0oQqAhFGeqJsRb19DkD5XhYTJcUIxUJFPkIF7Yvrmvj5EgHhe3uRPWnm0Aso4mFAwHtBa4QSxKmVp3ThSWkJGNo+bwgwzgtymeCQMjTZ66enGCYltQzQ1r+yBNmn/SEMhrThKWDOyOTOxBb69TRSCM2GX0DG0X3CcnqY6ie+get9fEn5XlQ07pO1GvO/PXh3i8sM7Iv7fc0xxEiZ4wyTtOy0jKGqCwQizHXxNXQ8roSrQjmpWwYcHKVU7xNFWVe52lIWQAQH4g1HuiZsyRoZNMAUhKeUtGenl519IAQ/AZl7T5uCtKOxZajRI1mM0wwzwQaqqW3KAH+MErbZsuc9x0oR0m5vwF1bw3x5CMhJQ2fXJQ+fHLho+Rgt8R0VDFjEyoCsRZlvVx0sfVQT5IuSlckUFj2KErGd21e0Jg0tWjC1CIbayz31vlV+V2VgYwm0WYk87mFg1lt4UCufEl/tnpKxolKQJeIrIabNrS8q5052QiGPX3m6nwNYqIiT0kghD7YqduHdptZEDRmnGOzE/kjQU860kT3XsoKWUcDGVL6X3hc9JNGRWCihff8A+Bua/3EVuUjUbB3fyGqc2I24L42mBBXh/oXuuAl5HChqXCkbg5QKwXeyIJMV0PkdSVWYeWl2zDkZGqH3HwkKXUWsZn6069vSGYjoc3x1RfomutownMdzwgYmpNf3bzx0YCeB/W5C5R40S+BvVErLu1YrBkVqbgIFX0605qKKOo6eiilxLuATVY8no5dZ89HWW1fgiJU3TyP6ieeDHxyUfrwyYWP5wXslpgAGlF+DxegBoIwIPKC1JCpaY6gKWNo5b1BPfjnKZHEthorcUlHunptjx01POkikIei5sDNC6r276kMnmhLDDmetmQgG13Sn61Y2WdXzx3MV+tSCk0isrpw04bIe6cZ2bDKPGPmqnz1RF0kHujBkNQH9mnH67Z5m8uck62aZRDDexmrZA21DDGo38PjInWidiSMIlNDwPeBO6318TGh+prWdQJYArwaJaqlowbkE91GSww7+plIz7Jq4Yb6pJ6RUgizX9YID11quJ5A5AxFKAKO9BoHnXRdws1GctIREkGWkJzNTqadvtuv62lic3z1eZl8KGrq+awnNd31dHP5lK2PVYQGR0YINBTJMMhyUPsK/eLnrBZ5XFTx5+n+6BVJqkC15P4C+KsVjw8AxK6zm1FOmJegyEQ3vv7FacEnF6UPn1z4eF6gpnWdhUqd1AKNAdebvao3e/7KPnvJBV2ZqfW2E5BCkDC0nCGlU5H3dCkRT9RYnf87s/xYZ0jLvv1wInZJR3qqLhGeQP61Mdz2P7MrjnWHjJNSA4YnxeKBbHRlr12xtseumz2Uq1LWmVKkDC1na8KdTM46XOGZM1bmql0Xz3MUKZEITYIwkPmo5iXNILr2MJu11rFP4DKE6b6M86iiSvTSo93DJpE7qf4hhKoVSKLSJbdb6+N2Teu6RlSB45tQKaaikNa4T+HlwtWvjfQsXG3YjYmEZrq2sLIBgRRKbbNx0MnUJ5xMmS2dk6hVlrCcyiHmcWjyT+1k7OueO+v44NRZgUI6JOsEw7NrDu5srmodS1Ak0EEdnSxFJ4hLRtzPMe122sXRU9Y+BFGpDw+V8vgDsNuKq7qV2HV2NfBuVPrD48wIiw98cvF8gE8ungeoaV0XRQ2qpQTBcLdIAFVbEETVYFSj3m8NapBsoCi6NOxS6aG6QjJCytyigVzksniyaV1HemrQlYar4SUMLVeW94K6lOJoNDD0v7PKD93bFO6dM5QPf2hP/9w5iVylkJDVhftfS6p3PFIXGpDjkAbL8bRVvXb5Bd2Z6gu67cbqrBtCQE4TbtIQufH2iVR55vTluWrHAdfV0JFOFC8RgJwApIGBQNPv5VExQGb0/jJK0L2UtZRRJo5zXLuPLcIdMwBaeUF9b1A3vrWgqu/ns8ojtqFJVIQidXofguQf84OrLg8Pzc5L4QYHZaZxyMlUpbycNt5PS46QrKaDpezkDNwPelPVFTuOLz3P1PO2EFLm3ECoMtTftaxp2/Yxly+JxT4WiEFqMcih40gTjTKCCBAH6Be3c0w8RN8oq/coqh4nBfwvcLsVj5+QV49dZ5soY6orUTUVXTyPbNLPJnxyUfrwyUUJoaZ13WTdIhs5zdbK5zCKnR8eqtCwOGU5zRx4wPXERZ2Zqte1JpuX9GdrJZLBgG6HXWkGXU9vC5vJ782r3PdgQ6hfSLj0eKr2A3sGFgY8qbkC+adY9OiPZ1e0pk1twvD49GTeuqArXfXijnTTnES+CsAReAlTyxXTJ44QZqTWseYsyUcCOTkY9MiMHkNlgCA2tn4Xj42KTKj1NUTcl7AGi7A4yhHtQXYJqVpnuyyj5nhIbxoM6LUB19Orcp6WMrT0z2aV7/+/adHOnD4uNRiJIFAdzHrWukfSzW/fP9j5oksz9UYZAfrIjJsEymPJEAlWsQnj9NMHjqtrj7euvcDxDNPQnLzr6aYQ0juv+fG/B43c8OfqIThCs2hlDgDm2AiFFECUACY6Dp54lHbtLhJsQQiPTpQH0H1W/OR0Uew6exHwaZShVBel/116WuGTi9KHTy5KCDWt63z577OI2UO50NsOD8XWdaabNQ+RMEUu6KEHXc84VBbo/+78yv2P14aGAKYl89bHd/TOn5XMVwLsqAz2fGVpzd7+oD4pqam2XeOFXenqFx9PNy4ZyNZ6AjOnCZHXxMC0VP5A/XQ3wAoWjeemCiAtQqKbbu1+to03oMspVLgv4jwMAql9ou3wgYDbF9AbACHAMzyZK2pxWI5nRBzP7A/qmdvmVe67Z0qkZ1RURaBqNiwgHcjJP/7xqtaLl+zL1QHdsgLD+xjz5RqaGCJ7EuFxMNHw5GoeI3Rmgm57u+bP6RhqnB4wchkphci7prWkacfGmkjvsOJsgjC7WSRSVBLAPh3hLikwiRDGJEc1+6jhhxg8BOyPWidSIFHgfahU0dkQ1/KBTy6eD/DJRQnBJxdPD6pt13jT0aGm17cmZ4UcaSRMLRtyPdP0pLa9yur++qKqfUfKAjaoFMiV+wemvaotNV2T0BY2ktevrN3RHjYnG1A1oDbseIGXt6V6Prazb2BWMj9DqOUZ9zyq5BxmkSE9JnoBECIs9rBf38LRkevyAr3b0qtSM8Ws2hXuNCEQR3aZiUSbnphM3Cuc98ywK80jUXPg1gWV+x6vDdkMp9W2o7owHm278MB7gX9ASW+r8xHgvZp6+U8sRgCDZIWHjoMpl7GRaoZO66IX0JeuKt/evmxNwMjZgMw5wXBTRduheXX7Vb2Gh+AoU8Ux5gES8zSIizqfACZZOZ39TKELDQtFnIppobu//dCH+25++MNvdz2jEujk2UmB6Kj0X8l4iwCsjj3+Op9clDZ8clFC8MnF04to3tPfcWhw6huPJWYFXKkPBfRsNO8FAP7QHD30g7mVx4rpEMOT4i1HEk3vPDQ4R5eIgYCWvWZN/ROjSIaJGrQF8CCqG2Fnb/MGabfEyoA1wBskLPNewDTZTDk2yTEEQyCwsLQH2ZTtEOmeoF7VFdIbB029hkKEomFKXo8tcio8F3l4c6A31a9NrnchJWFXRk1PGluqrZ5fzSi7bVNt6GdFjxI7FjsP+Bqqi2JsSmY6lvcplsrpVNCJYAbbaR5W9zwdOJ6uPX5s7QWFdtNc3jWDITOTXBXbtFHXPEkSi90sFkmqTitaIdHIE0THkdPYT4zj6GO/L46nhTsTjYv6UtX1ntRy+7oXdDxy9MLuTa2rBzoSU54OGf0gSuwtxHBdkFaYMijl0CelT3Ku4h/X/OCt177sS+Y4qxJRK175jJ+Qj7MOn1yUEHxy8cygKusa7z442PzqeHKGJhFJQ8uV593gYEDP3rKgave9TeHeYjpBSMkr21J1H9jbv8Dw0NrCRvJTq+sP9Vl6GFUL8lvg/3qbN0zYkmm3xBpkgEu9dXxOVlAnMmTRyCKQEnDAyBuEcojgzsettJMTcnTKAySNc51owyy3PJcRzsGNZm8urY0hBa7AcIQwAcrzXu/UVK6twfYMXR3n58DP+W9M4MeFXSYUoZImwnsbK+RVaEzlCGd4/+3tmje7Y6hpRsDIZQptp8aq2KZHooFUhuPUiQMsQSLGq60YgzwWgGziCDM4RmD8GpyEXRbe1bloqZ23ogEjZ+uaQySQChiaq4GkN1WT3tq+snv78WUD29uXDXan6p/MoB8GKlG1QTrquuwBdgBHUFGSQWAwfoNVUqTCx/MHPrkoIfjk4plFQ8YJXL2nf9bFnempOU24jiZk2PHMrdVW11eW1uzpDBnDAlNSGpfFU3Pfe2CgOeRI2xM8dO+UyIc/94ptE1mlj0FyIFaGx0+9LIvcIaocRMDWhOEIAEEgKEVmSGSPPGH2q8rFURCS6cvylZVNXjg9KHKHHg/0uo6QHmiOJgKAMD1pN2Wc1ilppzPsnmS2ZgANSBJsYIitNCJPGYloBDY7j3AbtVyLUk/t5DSKa0enQ7JOMDyr5uCuaWWtHexhnugmhkmWU3mXOJh4GLKKDuZwkMj4RERKiA80Nx3um7kQkKaeHydCIbEM2wgH0qaUQmpCioFMpb2zY3Hvrs4l/Qd7ZqcO9MxN5dzg6O+gQJGJUOHvDuCvqCLr3fEbLF/F00fJwScXJQSfXDw7WNVjl//b7r4FsVS+fMjUsmFHmnlNuN9eULn7z7FoTgoRRg2od4fz3u17f3donqaKBAXwU+AX1vr4hCH9mtZ1AWA+sGKWnnv5f0a7LtM8iZWRWmPKCQRcqUnA0XHNEHr3ET3Zdcgct5VUM6SYtTpXHamWwb4OLXdoWyAlPOHUZZ32prTTWZXzhibtEE0wnTSLSdPHJvbQOqEZXiWqAPKfrHh8IGnHAsC7UHbmGSZzWPU07fFja8/Pe2awkA6xosFk/8qyzfu0XSwjS5jACf+Y8SHRyGFhkZJz2UXtsADYaDieru3pXDC/J1U31dTzWU14p1lbIQnqWT0UyJia8ISUmkRI0ZloSB7sntu/r2e+e6x/mh4fiGW7k/WbJNofga3xG6yn1R3Zh49zAT65KCH45OLZg6qxGGr6x4ND83RPBhKmRlneM3ZXBvd9b17ljTuqgnf3Nm848YRqt8RM4EMoBcw88HlrfXwTnCATc4BFKOntZQybtCUuNNP69dGeVYOelnUQXiTnmXUpN1xuuxZCIsJCHNka6Ev2aSe1S0oQjiYChuUZ81fnyiIRT7oHxeHww3KrcToiUDks2rgQDYcgOgYGPfSwkf10n6SLEURpjVxtxeN7Rh4iaccWAJ9BtXR2Mk4twcGe2dPjA81zA0Y27UlN9zzNWKs/etA6mpuDwMM4RRtoMQUS4wAzaB2vrqKITN4K7ji+dFk6F6kIGNkMT1EMS+AJXXPDQSNrWEY2VxEa6KwK9Q8FjLyNkpZvQ3m9tAM9QB8qtZQAUsUuFR8+nuvwyUUJwScXzyqiQHm17eqf3NFb8fL2lBnNu8fCLgGUKNMN1vr446N3sltilVmNW9KG1twf0M13XjJlR2vEnFlYXSzoG2SUrPS7rIGp7wkNLuzx9LQsqFEFXKnVpNxwXc6JaKAdecTsHXL1vKOJgAeaAFmRc3uaMk57faXrcAnnYWKKx3hC33uKFIdE0M5qcpSjj0gtWFhoCFppZzOHGCKHMsn7Tyse/+N4h0raMRO4HCVGJVG6EWqd8g650NCcnBDSy+fN8IrUlqGK/qHyU6ZBPHTyBGUFPcxjL9Gx4mIj0Z+uKt/VuWi56+mmqeefkmOplELLe2YQoCrU39FceexYZWggMaKTV0OlRYKFqejOC4o4FrtBinbsNgWRt8JUUmJd4iGu0bcSHGdVwlrvF3SWAnxyUULwycUzCg1lZFU0QzsG/Al45GM7eo+u39V/EfAp1ICSQik//vhri6p+2rKkZgowC1gOnAc0LurPBq7b0jPX8jzvgYbwsf9eVL3f0yZOUAgkn4v0LHhhID21x9MzjJC7FBKtKZ+vDHZIffBRLRdw6YnmvSN1WbcvIIcHKXcO9fICVuHi6H/hUdE1iUNoH9MYZB466XHXh1S0gH0MsYdfMsS/F+WyJ0LSjk0DPlG4Dj1SknmibdXKZDZaZep5W2RlaF73vkC105cTp0qD5LEQeHIWu5lK56nUP+MDUxsO9c5ZLITnGprzpIsmpRRa3jWDQkivoayzNVbZGo8E0k+WqAhUbYtemIodI6XWmilo51Ljd+N29whrvd+KWgrwyUUJwScXTztCqFoCUNd5B3A/8Ghv84b20Rvf8bN5TfMHc58JO94lfUEND1G3uzLofn55zcHjYdNDPY0mULUJCCn54J7+Ga9qS013hPBuWFG75Ykaa8IB38LTvlnesSqmOeW9Us87UgQESCHwqoXTNV1zsI56v478mRiwEKUq2cOIe8Rdyxy5kPkkGNLv5BGRHqfl0SbKcc4vdKhM3O4psQgDNexE4yfAb6318Ul1LZJ2TANeCXy4P13RtOP4sqmG7qTD6bQ1reNoZYU2OKQH5PiEBk6OVixgN+HJdS6khIO9s2fEB5rnnFl9xRiInBuwBNKbUt5+ZFrV0daAkfedUE8X7bzdJxelDZ9clBB8cnFWIVBRiXKGdQe6gAdQ1uw7e5s3pOFEjUQTMAVoRtVKLAQahZTuK9uS1R/cM9CsedI1JNLRhNuyuHrbfVMifWNfFuoyjnnr3zvOt1ypH42aQx9bU7/VNsbIietARZ3mRL9Z1jk/JLx8SMjWOs3tqRLukKYszwNANS5XGbcSQpltXYAKx3cBUmoI72WslE1MER20a/fwhPBG3EMeGm2sxSWENsnALdHxMJjCowTJo9xEs6iW1T9Y6+MTR0WAmx/8TCzrBO68eNYDjZFESqs4MhgNmrmEZWYn3i+vwupyJnto5vipohWeFGJv14K5nYmGaQE9lxHiyf345V3TkghRF+mKz6o5fNgybV8K/Ezhk4uSh08uSgg+uXhKCKHqJkxUREFHFeD9HdgKHCxs11iYmoHZwEyUMVrxh1JHDaopGA7lzx3Mha/b2r2sMe1GM4bIRxzP/M30sgM3L6g6Mp5xGcAr48naD+7pXyQF8kvLarc/WhdyGCY7HrAJ2PDNso7064LJ64Wgh7GeFzUoInFV1IrbdktsLvAe4KLC++yWIXT3lZxPORViD3v1RzlwYu8u5pMihj5p/YLAIUQt2yhnZCdEECUSZgM/A35vrY+P27URu87+iO45b7yh97M1l7747rnGTEdGsukekR2n1kAiyBGSEQZZxHaip9a5cDxd29mxeHF/uroh+CQLN11PN13PMCtD/Z2zag8eKAsmJ63p8DEJfHJR8vDJRQnBJxenhI4a8EIof4zi9TJRVftHUYQiiXq6b0QVJzah0iEjXVVBFdrZcIp6gALCeU+7Zkfv3Es6080pQ8tHHM/cWGN1/MeKut1Jc6ygFRAO572qmx/pmFeR8wLHIkbbtavrb0qZ2uPA7t7mDSciCUk79hbgIygp7tHnMhX4ddSK31RcYLfEZqEiGS8BHFlPxn0pa9ExxCNs1g/QRYJaulmBweSDsUuIMO3Us3uC6EEARTLyKBXS31rrT3IbXRDNJW773N9vqFncu7OuM1rvrV6z8WDwHdlphDEZJCucwkDkYuBiyiYOM4fDk3WCFJFzTWN7+7JlyWy0KmDkzpgQFP1MTD2fnVO3f2d9tNv3F3mq8MlFycMnFyWEU5CLBygt06VihX2xAK44N1GDmY66FsUWzkDh7wwqspBl2LZdop74i9dOL6zLjpjOWuj7NccSdR/e079EAgFPau1hM/mZVXVbj0VNAxWZ8ArvrR2VgnnsgT8frZqdyF+NIjifsNbH9408ZtKOCeALqNbV0fUfGiplsz5qndyxYrfEZqI0Ny725hD1LmQWeXL6H9ksdrIcgYuYtEMjgEaOqTyKfsqOhqLcuQT+CPxqztCB49OGjv7ks4984ZIpyTa9I9wopqSPH57Xv/+QjKJ776JZXsYsNASdSKHhyAVsp+707uWsEzC3tq1YmXFCZQH9zImF4xpBD01rKjt+ZFbNwcOG7p62m6uPSeCTi5KHTy5KCKcgF/0TrHsuwytM7oj5SKt1d8TkoAhCcRtnxHbP+IAxfzBbcf2WnlXlOc8CvIwh5H8tqXno0brQn1FpmD29zRtOEqiyW2JR4IeoWpA/AN+11g93ZCTtWBnwfaCMsUQyiiJM745a8THCV3ZLbJ6Eq7w1vEEuZIo4jKP9jIyQk6QcJBoeQRp5lBBnojJpoEiGtm9o7lDmweDFRo9j94VqPU167vnHH/2bIYcHcTmFiPculsqXYRDjMAHaOY17OesEzC1tK1dlHSti6rkz6uBQ0YpAKGSmh+bV791VGRr0VTTPJnxyUfLwyUUJwU+LnLMwUcZUYYbrOVL1GWfPjx46Pm9WItcUcmSvoaIr/26tjz802cHsltibgfei0jFXjuzISNqxecB3UGme0QWYTcB9wBcmEmvKfDe2wlvNHbKRRrGZhHYvAxPWSTqEqWIPVcOuqGeCfEqvyyasS9CkTKfCubajU50p+9ofa0h1j7xPIyi30h84G3mISq5ERWfGdL6MhO0Eza1tK54UsVC1FbrRVNF+eHbNwcO65vk/kmcbPrkoefjkooTgk4tnHUWhpDCKKDgoIpEGdgFbgP3AIaCn4H5qAlejRKWGUBGGFlSHxYRfTrslNhX4VuH4X7DWxx8rrkvasdei9CNG118IVA3Jp6JW/OFxjxuLLZNT+Y77XeZTSVS7h6S2ixTuqJSHS4ggPTSx9VRdGuNiiLpMr3V+Wg8FEDjClEbQyDrhXGZA7OcIezhOmorC+V9vxeN/H/H+FgDvR2mE2CiSMfwengKxyLmBkKE5ufn1e7bXRnonkjb38VThk4uSh08uSgg+uXjGEEAVhIZQIX6HYRWrVmAvsBMlrHUU6O9t3jAZURDAq1CEwEY9rf8Q+OEpCIYBfAVYAPwN+JK1Pi4L9RfXAZegLNFHIoIiJO8anR6xY7Fa4AeA5l1KwLuWNeQQ+u+xRQKBjY1E4mEggKn8HeMMrcAlMEDMHdAW9euVUVXPIZAIrVr2deu6JwgQwCVAJ4exuIb53Df6OhTe41JUvcgKCpEM2wkaT4ZYSCm0nBuwqkL9XQsadu8OGjnfjfTphE8uSh4+uSgh+OTirECgyEOAYalmiUpnFBUU+1HE4SAqCtGGKqLs6m3e8KRlmu2W2GrgxsLrhYDbga9Z6+OTDnR2S2wdsB6VBnmPtT6eStqxcuB/UCmZ0UJWTSjxr88X0yN2LGYAXwMWozw/cNczV76J+WI/vdr36RLTmY5EkEJQx2aijKvTMSEk0MssOcSsQaPcyouA0XY0dwAAIABJREFUqeG5LroRJTEYlnaGYltrmC7q6SmIYrcD/wtsGC3KVSAZC4D3OJ7+woM9s2d1JRt0Q3NOm1i4nm64nm5Orz6yd3rV0fgEncE+ziZ8clHy8MlFCcEnF2NQlE4e2U1iFKZil8jIa1b8UesDulGk4SjKIrunsKxzZAvo2YbdEpuHSouEUATnYeB6a3180te0W2JNwM0oAvQJa318X9KOrQC+UTj/kaRHxR3g08X0iB2L/TPwDzBcPyGDaN43WC2X0iBuZ79+C8dYyUpm4lDBfs6k+0gC3cwlyfSsYbqDorJKx3U8hKbjeVWyv0dIdFyClHOIGg6NSLeUFSYXZVV+B7DFWh8/8Z5i19nBZVO2fPc1i/5w8fnTH4kAcsguzzmeOWmxbt41g5rwvAUNu7f6aZBnED65KHn45KKEcApy0UmJmR8VUHy/3oi/i1OeYUGrZGFKoAbFLhTZ6ivMO1BkYnCyFMYzgUI9RQtQjyJCj6IKPSd9GrdbYgHgRygfkx9Z6+O/Stqxq1BW522jNj+RHjHmsBD4T1SE4KR7RE7Dcr/FCygjqF3PHu2vHOFKvk4FH0QJiPUD49q7Dx8EURTjkgaZPlFdKxFCID0X3aiUA70BLw8Sg2p2UjGhiZqOEgUzUNGY3wP3vSH5u/gOb+kNKGGwtubKo9brl/xu6ovn3D/N1HNaKhfJ205ojDR3zg2ELMNOLWncsSUSTD0l4zIfZwifXJQ8fHJRQjgFudgIZ9Qu+FyAHDUf/X9t1OQxrG5ZJCBixFRU10yiBq9+hiMWPYVlAyiX0gEUEXlaohh2S6waVU8xt3Dum4DPWOvjE/tscKJ+4wrgLcB+5w18kqncjFIU7Rm1eRNdbDRewDKU/se4x/ZeTq33adbQg9R+zGXhW+KP2C0xHVXT8a+obo4exnangIegi0WkacIgkxahUJJouY7ruGh6kFy2wh3KAB71bCHMuAqe48ACqqWE7e7S8l/kLw894ly456iccULLIhpM6K9aeEfjaxf/34wKa9ByPV0msmVZT+pknWCoKtzXuahh1y5Td0qRdJ/b8MlFycMnFyUEPy1yVqChUiYj0ycmingUtTRguP4igyIfHagn/zaGyUgPqivkSQlw2S2xMPBlVMEiwDbgU9b6+OSRArXvSuAGIOe8hU/TwC0ocjT8hO6gc5hLtP/gqPb3E/Lm48JdzwXyHwhTzk+Ba6JW3Cu8jgW8DlVYGUC9dxUl8NDoZAk29eikPYTWK2rqBJ4HING0aqc3oesyTSNPEJjcIn00pIQ93vw5g17F7Eox4AgB7V5TcoPz4ra/uS/oPezNygBowmXttEcrX73oj7ElTdsbXU8PRIPJw9Orju726yueJfjkouThk4sSgk8unhUUJcUDI6aiqFcxGjLEcP3GIRQR6UJ1ckyahrFbYiGU8uaawjH3ANecygissG8DcCuAczm/pY6rKNZUSGA7i7GZiiCtX8XfRXLCtFmdLKPV3UgEnaXAdVEr/qtRr1UJvA3VUqvh0UMHi8hSV7RpT4pIWZpQWMdzXTS93EnkLDPbRSNbzrjrBDjkzmw+6k2fHxRFrxBJmLQZErYhgV5Zk37YeeHxh52LenZ5i5ISLVQT7mn46LqvPvjmZb+eKQR1hSvRx1lUYPVxGvDJRcnDJxclBJ9cnLMwUWF8C0U+isqiOmpQa0WRjgOF/7cBx4sRD7slFgT+A7iQYYLxsVOlSAr7WsBPJFjuO+mniqlAJweZJo4xjyBpWUNI3MNR/esjDMuGYaEkya90DmChXE5BtbKO2d5uidXi8m4G+Qg5KsgzhEQ6aHqfqK7VVNRCBNycFg2kDmsNcttpyIaPQYfXULvbXbgiIHK2QI4zSEksbCMi0qZEkJRR+Zi7NmHgfPX9wdv+n/Mh0sB84GXAZagCWg/1HfGt059u+OSi5PG8JxdCiCtQmgJFzJRSHimsezHwO+ArUsovP/Nnd2bwycVzEjrDRmpBhtMuxSLcA8DOxrTT/ud7Wt9Um3VXamoQ3AJ88lRFnnCiDuPLMspq903UkmVA7GARJlkEntQQVGHpn+IxsZ2REZGi6NYXrXj8ToCkHXsbSkNjC/C+qBU/KZVhx2Im8DnKuZSVWDTTBMjBbFkwK4OWLl3PcB1TD3tHo3WpjWhnLkk/4FWUbfWWr9Fx8xreKYmJg2Ea5I0l2s6j5VqimFLaieo82e6+kCNyBUuBVwAXM+xD40c0ni745KLk8bwnF0UIIX6EsqIeSS7ehuqvv1VKefWzd3anB59clBQEimyEUeTDNV0pPre1Z8ZFnelwyJXJ/qC2+f0vaPpCa8Q80Nu84XTqMP7Rm86/eYtYQDt9Qht+QpflBEU3Ke0DPC7cE/fQCT0MK670MJJ2TAe+CrwaRcpvHKGVYQL/DqxDRV8kVYQyy4Pzs83BOZrnuqSF3h+t6ptW03rfk6l3SMtQcLO7aq2Hphs4pxz4HYyAQMql+vZNleKEP4iGisaEGa6jeQJ4SJZzyH0rYSwuAl6KuvY6qssoQen58zw78MlFycMnFwWMRy4Ky5uATinHC72eW/DJRekj4Hr6Fzd3r1jWn62XErGp1uq/fkVda14XnaiCzy3AYeDwaMJhx2Jlcj6/9z7NBXIqiA66i3eLBKglJH7GXv3/EUdZzCeBK614/KQuo6QdqwN+iiIfH49a8bsKIlyfQQ3IbcVDSmBTw+pVMkL1jClHQpkFIVET6dsZ0dLH4MzqLPLS0De5q8/LEoyY5E8ZsSkSi2X6to0VYmgy8qWj2ncthjuJ9kqdR+VyUt5iqiljDYI5he0lqo7mlGkpHxPAJxclD59cFDARuXguwScXzw+EHE/76uNdyxcMZmsAHqsLHf/syrqDriaiqGhH0dOkHdgMbKscdA9tfu2R9wfzcq1cQd79CheRR4p+upEFImCiEcHUP8TjopUy4GorHt8z3jkk7dj5wC1AiiTvMVZwOap24QSxAOgM1Vfvr5yzuj7TJb+/5H0dTyxcdfvd0VccQhV+BlDtvqfsEvGkEFvd5UsHZUVdQJzaOr1ALLxl+rZNpyAW40FDebxEUWRDA5IyzAE5nwFvFuVUMwOTmoIdvYYiYilKU0vm7MMnFyUP7dk+gXMVQogNQghZmDaMWH7BiOVSCLFOCPFxIcQxIURSCHGfEGJZYdt1QojHhRAZIcQBIcS7JngtQwjxESHElsK2A0KIe4QQL3uG3q6P5xAyhuZ98rz6bYfKAv2APL870/Sp7b3ThJQ9qMG9E0UswsArkfLTZSnvT2+6ZepVV32xoenmJZWRg3cae2QEXZZRi1BamCKPh0B4/8QKqXHrRMQCIGrFHwVuRVLHMX4hI7yWUcTCQ4h42dRFNXafftuy9+/5zfy39h7yZt9krY9/D3gTw8ZrU1BpiglxwJszc0BW1p8JsViub30yxEKduopMtDPcYpwRaeZrT/Bi4zesMG6jUv8BaHeQEtvppgeDDDPJMxOPKYX3VIkiez58PO9gPNsncK5CSrkOQAghRy1/RC0W16MK2z4J3AksB6ajCkDvEUK8HtWa90bUD+4PgB8LIfZIKTcWjyeE0IDfAK8BPlrYrhz4PHC3EOIKKWWxQv+pYD5nGIZ+DmCkfPdIYSwP9fRenLKFeTG/Xlzvjvj7OYWkqbnXnFe/9euPda5sTjnlL21PTeuydPu2+VXHRmyWBtIzW/Oxma35yowlEm2NRvTg9EDl77yovFr0Oy+tSQdFkCbbFn1RW+aCnRL5AjR3C0dOeRL7+SEZ3kYtF3qfYL92PXLkt6UzXN8cdHPl31n+zxtvn/1aA/hF/AbrOIC1Pp4Efm23xP6IKqJ8DzANdY/2MOIz6fAaatu8qbPOkFhsLBeJs5m2yKOiLCckz4WNJo4Q5ghVgCkFScoJyEoqZQ2CWqplJSYWGjoZNBw0JBpZBGk00ghy+N0pPkoQPrl46khJKb9R+H+/EOImlHTzD4BlUkoHQAjxGeDlKP+GjSP2/xBKhOgnUspvFpYlhRDvB14CfEsIcbuU8sxMosYizWmEn59jKOpIFBU2i8s0VP686C1iogarPKr6P1f4vyxsI1DiUqOVO/XC+iJJyY/Y91kfEAaCuvOxNQ1P3PRox3mNGSfyjsND83qCevZ3M8o7i9s0dTq1M+P5BbmAsDWJF01LL5p28wB/2hvNzVmZr2/K501hUPdEQ9ARHm5NlXMsYsgvr+9Y+64/ND7WPtHrG6/idbKRiHsLQ3Id07030af/RrmwuojIYLBy/jdX/sv2+6a/bBAlN/7z0ccoeKbca7fE/oJyOb0cJeMN0JuQUX2fN2+pKfJZweQ5XBfdFEj5NBCLieAxLCuPkMAgiEHgKCYF4ztpEKKcgIxiyDAmZZQRISwjBLDQMAFwEDgI3MIkEXiFuTKOLSWU1rvxMQ58cvHUcceov/cX5o8XiUUB+wrzeaO2L3ahfG/kQimlK4T4FXAN8Gbgtqd4nq08v2suiiSj6HY6Um+iqLbZgxK2iqPC4gkUmagtTDVAHVCNSjk4DP9MFr9L2cI+xfnT+jPaZ+nONWvqn/jWI51rynNu8IN7Bpb0hIzcgw3h/qoBt3zBoewyRxdZKcZGZxI53bvnSGTwNTOTFTX9jrEgkTP215mDrQQq6zynYY6eu7emdd02lHnaRmBHb/OGBIAdi70C+DfRQav2dQa8z7FWXsUSuZ+k2IbTb1XP+up5H49vmPbiVpRJ2k3xG6wJpb0LlurbgG0FE7ZXO1J/a7vXtDxKQrexssP8cSxcdMND05Zq2zc9Q8TiVMgXpqRwgD4QYx8PBGBIDYMgAYJYBAlKAwP9xD8DHa2YuioZlJoRgY8x8MnFU8fxUX8nxlsupRwSqvcuXFwmhIgCCwt/bh3n2K2F+Xk8dXLxfEcxBTJRl4FAtR3OA5YxHMUA1X2xHXgEpTtxlOEOg6rCVCQeMdRg2oTKuxfTLhrq+5YtnIPNWUpTtYfN7LWr6ja3PN61NuhK/dqtPSs+t6RuW7hVLvGEcN1JRKo2dlqZlfV2KB8VojHjyLmD+ejhavpSppZ7mzVUfV8uUtHqmW9C1UiImtZ1+y9+LN32iUXBVy86kGu1cjKv/ZU++Xv2ybex0P00q/igOPLvqz4/sGHai3tRRZG9wB9P9/1Y6+PHY9fZ34+QnLHWeKz+Leavw9O1I5UACVmWzRM4iSh5aLordXOxvnNztdY/2l7+XIYE8sIjT4YMGeWrUlosYkIsPPUmPp7L8MnFU8dEg9Vkg1gRFSP+PyAmbvxvONOT8nHGkBRqFEYt11Ck4bXAGxiOduwGHgd2oZ7oxxQO1rSuM1BRjlqUw2kTMAtVWxBDDbwOJ5umZQrTGdWB7KkMpm9YUfvEFzZ3rzY9jOs29Vz8vaqKRLdlTJoK8xDcsSeafd+aAW1vhdk7pydfPbMvX32kyuwXQfjXSF/sE4n67bJQ81mecOf0l2tv/tQn6lypieZZx3IDa7bZ3aseyPQumZvr0VbQ1Hrb1CP33/ViD4904X1eH7/BOlODt8tTRC+533nJnvudl8g52v7wZcafml5kPDC1TCSCLrqXkGU5F0PkpRmcr+/dWqf1nL4FvA8fPp5W+OTi2cVAYS4BS0rpqwGeezgpr16AjiIJSwvrtZrWdQeBh1ARqN29zRsyvc0bHJSHSBeKhJyEmtZ1UaCR4SjHPGAOysFUFI5toNIrReIzYZrlsbrQ4NcXVO24ZkvfC6Oe1N8xmAh/J1BhZzVtwn1MRwbimKk7RPTwZXpq+t66YO+8nlz1jP581ZEqo3+5lW242MzEH8iH+6NJ11q5MzsPyDgGeVcgjjWZ5funB6p+8epyUS1d81PR3oHKivSqK50vHPnOfddmhBs8hFLCPG3ErrOXAh9EdWpIgAPe3PQ3cx85eEvu6kMX6n+veqV555Sl+vYGR+rBer37QIPWNdrx1YcPH88ifHLxLEJKmRJC7AQWo55mx3g1FCTI41LK/aPX+XjW4KJs14s1BAIVmXgPhYhDoVbhPpSoVet45mS9zRuSqM/8pM+9pnWdXjjeFNST/2JgAYp0FI+jo3QVUhTSK7orte4BI3ZnJGK/KpUKNeQd8/L+RMVPq8sHvHGiYpqHLiTa9vnBrU9krcyFVqYhIjxzX22gb25PrnpGv1PVWaMnrg73LdzWFdi8ZHdulZBSy5siC6BLZFnay5Wn0AI5ae2dGdj68aH59V+uPlp32ZLfz9lYuy/2sGfeRVnXP9a0sgPY19u8YVJL9dh1diWqUyrJOGmjPAH5gHtJ3wPuJf0VDCTfG/zBgx82bg6jiB6F63G6tu0+fPh4muCTi2cfNwPfBq4APjtyhRBiNWqAuoThQlEf5x4kw/LQoFIp8xm2Su+raV13LyqysasQ0ZgQvc0bXFTNznFgE/B/cCLNMgVFROegakPmAxE86cXa87M9Qdn9NaFEmfDci5KZ6EI7Z106lIreVRE9qYROSISZl8G9swLbhsr0FMBN6eqd10W7V6elyO+vDfTN6clVN/S6ZVaNNK/qG7hwoxMSOVPYo48TyEnrSLO5t60h1KW1L5x3cy7a/4mmHVXX1O03+rJl1bvdYJF0aTWt6zpQUttbKNSvFK9H7DpbAJ9ApQtH1zKNxtRBKv/w9ezHvvLxa6+VdkusFmXs9lqGi6YzqOig35vgw8czDJ9cPPu4FSWZfI0QYgDlZTKIIhQ3Az+SUj7wLJ6fjzOHx8maCBbw1sJk17Suux+VKtjS27zhtGsRCoPwscL0EEBN6zoRzng1N36l67PJiDZl4xIrdWhaoOJn08rdaNxzFqeygRemM2Wdpu5uCYdO1F8EcjLU3mAcbmsyu4rLHs6HBx7Jh4+vNTONfZ5uHygQjKput+yyhlR0e1ewI5cfFk8sEItQvMk4eKjZbBUDU2aCpv9lqDE9J5Cy3t24S7vBtOd8ONH4aJdnFKMQIeBS4FWF6yRrWtftAzYbK9/VoB94yUtFsuGQkJOKNDaiyMnX4jdYEsBaH+9BFY3+0W6J1aEs6l+BImCCYZ2KZ72F2IeP5wOe9/Lf47iiguoGOIIa4EfiBuBHqO6Bk7aXUs4oKHmO3mcmcD0qZD4S75VS/qhwDjrwz8D7UFXUWVSk4jbg+6fra+LLfz8nYKKKPDVULcVfUJ/N9lNFNMaDHYsJ4P3Au1AKmZ4n4Hi9Edy7wKyYtsRZpoVlNB3Q9G9Oq0ocDAdcK+uZrkb39vnWZrSTReLqNcf8fnn7C7NSc3NSuMaQrJiRzJdFLE882BdK/ORYZbFOiGBWhjvqjaO75gT24wZN7fjSi9C8PJ5umoHU4E1z/qItN7MNW51g50eGGjdn0Ma7j5XUds6qFYPN89HcPBJXJBsTWt+MftE/PaENxlJioDktvIBEdeX0AR+YrLX1xPVpiZUDq1HfywsL119DtRr7DZHPHt7O+EXLvvx3ieB5Ty5KCT65eM5hJNFIozRT7gYOjlejMRoFYvE+FHFtZzxfiwosXsX5XgAzI4T3YFeo46+Lw/zsdRVHHVNUMHy/FI245DutwalXhAYWDgxqhmaLsNRxZtm5YMiS2jd3VHVtz1vZYE6Ge6r0tm0LgrsRAtE/faZI1s9Cy2dwzZBXt+/xxkiv/e2yjvOn6Pnye3ORw59L1u2S4zVauoahdSw5H6mbCCcnhSvQcwZGzlDnJ0BIIZJ1OTE4NeU1bf8vWXvwCVSrds/pXCsAuyVmoNJI56EE6mYwPMAN4huRPZM4K+RCCPEelFbQksKi7cAtI1WNhRAXAH8fsdtLUDU6VwOzUd/D/5FSXiGEmA+8FyV4OAulh7MH+C7wHTliwBRC3Ip6KAT1QHoB8HVUxCwAPAB8SEp5aJzzfgHwRWAtKpr2GMr47z8ZfkD9a1EpurDPIuBzhfOvQN3/vwG+JKU85+qMfHJRQvDJxXMaQRTREKi0x2+Av/Y2bxgYb+MCsbgSVaszPrEoYgrlvIQ1aBj0kuYRLrG2xg/VtK6rYbg25AJULYenS0/7gXF8WZ3jRlKedkIobIGXtXL9wvvKnurBA9VW5xOLgtulJiSuaWjtyy4uRC0CBFJ9XsPuLQBLDTv6n2Vda8uEF/xJpmLXdzJVR086NwmiZ95iYZc3ouUnbJuVoKF5IVl96ADBVFEyW0OlO46gROr2owTQ2oHuU0WC7JZYJbAIRTZegEq3FDVJEqjIhv8D+fTgKZMLIcQtwAdQtWo3FxZ/CFUQ/C0p5b+M2v56lGXDPai02jdQ37e7UKKHVwghvoVSUb4CFVUMoSwcbgK+KaW8ZpzzOIIiE9uBG1GCcxcBv0BFtZeO2n5d4TV3F15nN+oevAXlR9MspRSj9rkE9fCxC0V+DgAvBn6Mqk96gZTyyfjoPG3wyUUJwScXJYOywiRRTz+/A7YWn9ALxOIKFLmYnFgUMZ+pnMcKKjhCkB8C3yioYp5ATeu6MmDBG+8c+ufKBvcNl1+YKO/Laq6HwPSkp3tSLiIX6txoZK9c0HTXkYpABkD0N08XycY5J6IW9Xsew0oUi1u5NJCsvTbSu0ogxY2pms135sq6i+tEsq5O9M1Yjp5PTzyOC4FrhmRlfJcsPz5ajlxHCdOFUE+gRd0QgWoBPowiHvHC352oaMeYTpRCUeg81FPwWtRT7ch24CSlJ6H/bOEpkYuCd9PvgZ9LKd85at3PC8d/rZTy9hHLr0eRi3ullJeOWP4PQLmU8hYhxKeAASnlraOO+d/Ah4GYlLJz1LojKF+pN0spfzti+c2o6MhKKeWWwjINdT/OBBZKKfeN2P5SVOSSkeRCCGEBB1Hkd8HIzkEhxJXA91HRi8+c6ro9k/ALOn34OPdQ7DzRgBeiwqQdNa3rfl6ecO/frZ6krkQ9sZyOxbfGXjTm8UvqWQS8BfUEdPfIjXqbNyTsWGwqKppxX+rzLGi+QEzt9Ax6I3owq2vmXiOQn7Eir339b51rP7S28ZE2K+SKZP1MNCeLZ1jSGuoaSSwA7slFe6Zr+T1XhAcXfzTSv+y4Zz621bES5INBMTBtMZqTnTRA4JqWDPfHZdkYYkHh/Y/s1ClCoKJBy1FRmeK2AtBrWtcVpd5bUSHtLi6f01v4eytwW9svDwRRofFZqMLQZSj11eJxQKVSUviFos80PlCYj/GrKSx7O0or5fZx1v9q5B9Syp+O+P+NE7zedtR4eT7wh3HWe4xVod1dmM9FRUpAfZ9nA5tGEovCa98jhOhGifaNxOtQXWL3jyNJ8AsUubgClVY5Z+CTCx8+zl14qKdtgChSfiya8r504/urQ6//S3LXwoO50xnQBGpA/BVV3IIy1TsP+KTdEjtsrY+f+LGyY7HXAR9DPd074ZvYF1wqa8syeWduW962A0L0LNMPpsq05kjMK//6Y50v+tCyBX3dgZSFayaFNISsiI/JLwN83648FtOdyCuCyVk3RLtXfnSo4fGjfQvnI4WG5k0sHueZFqY9JKsP7TtDXWzJsMz6aOVOgQpjz0ARqZE+M1CIVEy9fE5P4Vp0o4jI9pmJXOaNRxORtT122dyhXGNN1p1pSmaijNlGqq0W/WWeEY+Z5yHWFOZ7xlm3Z9Q2o9E6wXKEEEHgKlQd0yxUqnIkqibYtUdKOToaViwYDo9YtrIw3zvJuY0mF2sL8y2jlhe1kvqAKUKIJinlqVq4nzH45MKHj+cCpEwuOpBrqu116u+9KOLd/aLImvkHc31v+9PQkRc9lumfWIOTJuBB4NvWl+Ku3RK7HuXY2wB82W6J/ZO1Pj5gx2KvAT6OIjM5ANFFTvyS/fIdLJZp8sEFcuPUsJMAuuWFRNI/lvpND2RWf3Rudc/xur4qGekZIpiqQKUoBhkhgiUR3Jiq2dugOeHlpt1wvTX0wo86phjQ8hPniaVuIDzXq92/Dc07Izn0U0AyPPBPBB3VQjwXVZcRAMThsoD7tSU1xautAbqQMluR84ZmJPP5Gcm8NyuRE/OHctaUtBOpzrq1EceLaBJHgKtJPE1KdFWm6go1IOU1cIQkr0nyAlwBXnE6i++7lFC0Thjv/ikuq5xg33FTW0L5L/wBVcx5I/AtoF1KKUd0FU5Eccc7ZvE+GblP+STnDWMjcDD8Xj8qhPjoBPuB+k775MKHDx+nB+FJsXRvdkFtnzs1FxDp6kFXSuDQdLPyP/6ldlVdn5u+/PahQ6+5P9UVzJ9URFWPKnL8ghWPuwDW+nif3RK7FiXcNgW41p4W+yvwSUYQiyK0X9LvvYi8XM0hKk/88NlCUL3lovOP6bez7NZt20P/ZrfsO7bmzk86S39bhkpDrEY9sQnUE33CRst8Nlm37b+jPRc0627jZ5o32Z9rW5HOeMY41EhoSN30avZvwrTP1JfkbMBl2OdlUkghtIGgbm4J6vqWGiuA+l0t/rbmdE9mq3OuVmu7emXONSpynlGe9/Ra2zVrsk4g4kgj4nhG2JF6yPWMgCc1w5PC8NDM4Y+zdCIfEvKaECv7n9LHOoDy7ImMs6647Ey9Zi5EEYsnpJSffgrnNhmKXR3jnTeoWqvRKBZ1f1FK+dlx1p+T8MmFDx/nMHRXasv2ZBdXDboN2aA40SopgIqEl5VAMiwC33531ZIfv6ki9+Y7E4fefFfieCQjK1E/Sp+24vGTWiyt9fFddkusBfgUGV7NEl7DNnYz9kk+KByqxVaulS/jvYWXlQCOq3XVRHtffX3FDU98dPAbS78b+mD1wt17DliXxY8Df6ppXSdQ0uXzUaHgNcCUXs+Qn2hbZn657oC3KtITvKZxR8UX25cNuGgjXlaoOovy9r2EB8btljnH4DFJFMTVBN2WQbd15j+3QkoMD02UELcAxKpe+62/2TBeCc1p4zHgMpQu0Og6hIUjtjkTzCjMx1NDDp3hsSbC5sJ8wQTrm8dZ9mhhPmO8HYQQzajo2t3yHOrQ8MmFDx/nKIy81FfstpeVJ72abECMq8EggEjtk/dhAAAgAElEQVRG5iMZN58JCv1/3lyx4NeXlS14w13J47Nac//wyt/un8jQ6w7ivJEgb2EZOXo4TPtJA6SJyv3eGP5M/E9JOzYb9WTXCdA22NyQcSw+cNEtM6/69Xf3PBK9MAXcYrfE/tVaHz9W6GxpLUz3AtS0rqs0H/nAv/Qgm7404+H052f/depFFccjHwD9W30zUzhBByfgCC8YktZQp6xomzA3/nyBFIK8jldqRuzjed2cIW5GkYt3MLbA8u2F+S1neMxjhfkSIYQYNVBfdOanOC7+hiIvK4UQ88bpFhldbwGqUDQOvE4IUSWlHB2RuRmISCnvOkvneFbgk4vnD6Yx/o37XIZbmPKFuYMq4MsW/n86nRTnJEIZL7h8d3Z52PbKJiIWY/bJSjeadvOOTuDGq2vyqYj2VVrX/Q/wh97mDScf4795PQbzeQ0DVBLlIpbxR/5OBgdVb9AI3GTF438q7HELSgvCcD3Niw/GZoFM10c7q9+++ucby/cl3omq0v+W3RK7xlofH1OwFvrenZWo3vzt8Z1vzN8648Gqa19+w5o3hxLBvO7Yt6VrXC80UCFJebL6SD+CRobN2fzaAx8nIKW8o6BJ8WEhxA7UACtROhdvR+lc3HGGh/0bKtqxFvimEOJLqN+S9zJMWJ7qeUshxD+hOrV+WRAB242K7F2P6uJaNGqfrBDiHcCfgTuFEB9Bda/Uo7x4LgLWnY3zO5vwdS5KCKfQuTjKOC6Tz2GIEZM2YjJRg6NEDUhFu3KbYRJio3LpxaK+c4qElCfcyPLd2ZWGKwOjjcImg+ahm44M7JwbfKKzzuhDFSTWoKrWfwTc0XbhgQzDbXqd1GDwSs7HwOQ4HdzNDlR3yQ+BH1rxYS2MpB37Z+Ad8YGp7v9n77zj5Crr/f/5PqdO3TJbk9nUTU9IQgkJRVdF5YJeQL2KIk0vggUEIyoohCiCCLFRxAsiWFEvP0GBSxGM0gLBVNJ7drJ9tkw9c9rz++OZyc62JJsECMN5v14nkz3nzJlTZs7zOd+6o6txtiqbWYIbmFW/YWNIS50j340ERMn6GgBL9MWxggkY0SWGBBHnMRki+wIAcOb0J6qves9P5kvk0J/XfnL7/SsvMay5f77FPv53LoTpeHb+PQW/iQRx7QrX1OMdyILO7Pl/+ce+o1Gh80KI7/Jx+VnrAdwzqELnBAxt2QAUtWAoWrcMYpD/Twi3XheAJyHqTNxaWE9ohP11M4pZyjm/iYiG3IcH1a5YCOAWiPikHEQ9m8UQv9MFnHN1mGOdBuAGAGdAZK20QPQoumVwWuuxgCcuSgiviNZ+CMIqp0IEFQbQ31NChhh0C1UeASEuCtUYC6W4s3gbBq/quF0xa2tuHidwW6aRUzQHwVwwxeb61onq+li90j5osQ6gEpynvvTb3h3X3hc/UbWwD4Xjn4E6nJRvWf46OrERvwDws2JhAQApIxpyOf60Onb87KzlJ5czKaileo6PruoA8NegHvuRsSxKAG6DePr6ob449i8AiC4xPgbgagjz7gA+Pf+3Yy9e8KtZlqOorzefdN9lp9y+uHh5vgV9HYTPeQJEC/qpEJa44vTPgujIoZQCIEuQoyUuSg0i2gVh4Jj0du/LkeKJixLCExeHDEGIDj+EAAHEAJyEyJjgECljIQjhIUMMYink+2+8GTs1bp9V37jHnGlLZDnSoRdlKnQn3TVO2byrQR0yeAMAOMfk3eYMX45PCmbcxCWP9G0+a3m6Uyrc3t+HWYhiIhR0wI+z9W8NdWsAwB9XXb54QuWuGxJGWa9pq745Y9atrPT3pCBSXr8Q1MX7jGXRbwI4HcC9jYntqyDKFPdhhMDHz5744NxLFzxQOSbcsocI3wvqsYOatCPNTT4IK8tYiAqJ0yFa0deg340iod9dZsCrOXFM8G4WF0T0FQBVnPObBs2fBWAdgLs551e9Hft2NPHERQnhiYsjxg8hKAom+CSED7QDQnxMhXhyLgiObH6dI3I3MYfTtJ1mY32HPd5SyHDZoccXEAepFvfF6uQdWydpw5l+wRxOs7fmZlR1O2NMlbJpH0lpH1PGdNipy//Qu/W017O9TMY4/Bf8qIEFwg4An9cXD8wyiS4xSJHM/7n741ecFVSTKgeLHx/996p8bF4VhOvtiqAu0l6NZdH/5hznPWB+Tr81dz1Hf0GwwYQJrvPClac8VxXsugjifH4nqMeeO9TzUEykuUmBEBj1+WkyxHVryO9n4XdScKV5Ba/eYt7l4uImiNTvKyCCUW2IwnZ3AghCuEVG+q28Y/ACOj08+slgYGdMHSLQikFYO7ZBdEfsgLBsnAjR9MuXX8eAeDo/ZKuDlnOV4zbn5oTSboWpUpaPIuewYLFoqZV3bZ2oDissZItLczcbc8qSblUhldVvcNtnOHZ3ueS76atVJ5y4zsid/3jit8eX5R4A4V6IwfgKAD8atLnZlqNOfWjlJesWN92+qCbUvrMo6L8LIu30IwAeAwB9cez+B269tv44ad01P9Kvblts/KiDD0g5BSAsCyEO9tWqYNfa/LxLACxNGVE3qMf+cajno0C+b8i+/DSAvPCogig4VHgdByE8CmIE6I/DYfl9tCCEh1U0eUGmHofDwxCFsRYD+DGEoGiBKFX+3VIQFoBnuSgpPMvFmwpBWDWC+b9bIQK9XoEQEzMh+gacAOFqYRBulCRGeBKu6HVCs7fm5skOV0YTuAn0C4vWWnn3psnqdgyT2qflXGXexty8QNYN51QathiUmuP+XeOUxO6o0gyiP7/+t11d9VnnaoiB8+v64tiKwrrRJcYPAcwnuPYd51xTe9aMJ3qIUBzfoUGIrguCeqwjusSoAvDbhdIrymLtjmkWVOeSzIMvm9CKz8dYAH+ILdXvBYCUEWUQlULPhxB6S4N67NnRnJsjIdLcxCBu/JX5qSI/1UEIkZr832UQ19nBQJFRECMc/RlLxZM76PVdeQN+N1su3i144qKE8MTFW0oA/WV5YwD+H0TEdw/Ek//xAD4AUT6aQwwk3QBscI5xLXb95D3mTJfBtmUalVtlv7CokXdvahxeWATSrj5vk3G8anLdVIcKl8I24hVS67rp2kbOSAJQQ5xnH/97LDW3JzeRgDYAF+mLY93RJcZEiEj2FgD1Z814/PYfnXv11/LHVLz/tQBW3PXCld+568Wv3gQRd9E2lW3x36x/5wQHEr8sc98rKYQciMG7A8BlsaX6/liMlBGVAFwH0aAtC+DmoB57ajTn6K0g0tykQQjOMIToDBRNZQDC4DysWLxcM3mFYqOCudzPOPzg8EOIMU1yOZMdMMnhTHLByAURBzHOGXHx/5KSIASMydn1v9nQOlyWlicuSgRPXJQQnrh42whCDDAEYDWE0FgRb1huRpqbyiA6czYBOE2yudbQajVEW6wQERkuG10aLHGQJoTFno2N6rbhhEVFrxOesyU3j7lcshQaEkBZEBadEWnfG1O1zZwNSJvTqwy77tcvtEanJMyE3+GPA7iuMbH9OogUuAyE6+fCzdc1fhbA5zHQ/UAAxv5p9ScfuvGpWy7OL+MAUE0dyl2+rywEOL5l3LZmlzspCCEstg/ex7zA+AZEB9ccgFuCemy4DpdvG0Y0KkEIpGqIlN9KCAvHWAiRFYHob6FCWDGKe00QAMklwFTItWVwSybXVAi2TNxhgMvItSXAkQBgaGrjOxdOlbp7RvWZjme5KGE8cVFCeOLibYcgTOY6ROGnRwD8X7xheSsAbFw0cW5zvXzHivm+Cf86ye/PqSSDg4fTTk52Dv5sWhAFbdXyno1ThhcWY9qs6mm7zDkuwRnOIlK0jb0bp6hbh9sGALy3LTPx+rVdMytMp2evM+H7F3Y9fQGEJaMOwPdiS/XnUkZUB/Db/PEmCu+1HRZe1zpv/hV/um9dIlc2oJqgDxn2gP9zp7hggWftD/745m9/8eaRjjcvMK6BcJGYAH4Y1GOPHuw8HU2MaLQQHFqH/uDQiRACohr9VqlCmrMDIYaKYzS82IzBjMH5+NSw58UTFyWCJy5KCE9cHFNoEE+uxBy+8vvLOns/+2jig4wjDaDXlEEr5vvKnz01UPfaXL3Ologkl/NQyjUlPvQaEgdTTa631Mm7Nk9SdwwRBZxjym5rQkOL1WgplBvOIrI/AHSkbQzihjWd09/XmpmclHTpa3Tdnn17P76NuAQA/xVbqlsAkDKiCwHcDuEa4gCwrbNxYs7Wpq/Ys2jHHf/41pDiPgS3+kf61yrPVh5vZ4Q/6otjD420D/kYjKsAXADx9H8vgF8H9dhRvXHlrRB1EIGd4yFiaKZANHdz88dWSEkuVIH16mkcLp64KHk8cVFCeOLi2COYcgJj2+z5is3DkT6n7xNPJrefPah7aUYn9uKJvoqnTw+MWTtDr3YZyGe4tj/LLUK+QJbF9T1RZeuOccrewaJAcjibvSU3I9Lj1I+UcVIQJ81jlO3bJii7DyYsACBoudL9L7YtqkzL9WvLA/b1tWfFaef7l7b+93vvK6yTMqIE0Z76RADtSSPoX73vhIWqZOQq/d36TU9/b+Wq2ImJos3qEC6ki7eHGxcC+ByAnQCu1hfHhnUR5T/jywAuhPh+PwzgzkLK62jJWyPGQVggpgOYg6FVQA30VwH1bpJHG09clDyeuCghPHFx7MAcThNjVsO4fVYjCMgpZGR8pGQ1JgezrvWfz6Z2ffLJZEs47Q4YIDsqJeXp0wPVTzYFxnVUyQHmcor0ONg7Vt24J6oMaSPpy7racZtzxx0oIyRfFlzb1XCAIlsjMHNPZNYtG3bM0LnNfz5ufO6xWdlVYO4vAfwx3rDcBICUER0L4DecI74qdsKctBkoVyTLCKpJNZkL5770yL2vGpa/MJA0ALgttlR/HACMZdG5AL4H4T74nL441jfMbhQExqUALoMY/J8EcGtQjx2wb7cRjRKERaIRolvmCfn/I78dF17/krceT1yUPJ64KCE8cXFsUN7nBGfsMGf5DDdkyUOLYhkqSakAU7Ucd857Jrnj/MeHigyXgE2NavVT7wlMeOhjZb3xSjkNkdq63wpQ1W2Xz9xmHie5XB4plVVyIEsOV7ZMUte11Cmdw60zIraqsNbjTju/Y5tyUeuOMlt2MtcsqnhhW5kaggjU/GG8YfkaAEgZ0Yt7MuXXrGuZN0aVc/trhUT8Xb6nt/zHrrtfvGonROzCBgDXxJbq+8+JsSxaBVE/RAJwg744tm643ckLjHMg6gP4ALwA4IagHkvt35Zwb0yAqLmxACJrJwTxu6D8OfSExNuNJy5KHk9clBCeuHh7USwuT95jjh/TYU9wCe5wmRrFmAqxRJBpI4iMCggf//VjX2ncAJHS+RkA48G5Mz5mqZObramORLYtDV8hVLa5Shy0Yaq2ujMi9472eKhn3ERK1U5SkDNu3/bv6hMzLbnN5UrXF06pf91mVAaRJfN3AD+/9N8XuWdOf3K9JhvMsH37hY5ENpX7+vTv/N8ta9a1zJMAXBxbqg8pbmUsi8oA7oKwbDwC4Ff64uHjKlJGtAmiuVQILtaz7+Nu9hBq0V9nRIYQKjmIOiMHvA4ebwOeuCh5PHFRQnji4u2BXE7RVrt2UsyaJjnCijCaSpsFkaHnuH3+3xLbP/VEwtYsJAF8XY/F9qdpRpqbaNIec97M7bnb945RTrRkskJpJ6vYQ2/SisU1l5G9doa2ui8spQYvPyiOLLOWuaeDuRZcSZvsNnfcs3lljeZw6aHG8KZfTq1ohrAE1AGwpXUf33lK+8wTb/zgzQ3d6cpMcSXOoJpU4+kq6bonfnjV+m+N+eOBPtZYFv0vABdDWBgu1hcPdXsY0Wi1+0V8zD0X3wChCp2wpFuwkzagG8Kyc8gVUj3eJjxxUfJ44qKE8MTFW0+kxy6busuc7jN4yJYo50iH377dUEnKqRTyG7zHlunKVbP1J+INy/dfTyManQTguwCie8bI3f97ZmjMs6cHxpsKsUDGNX057gCAanKfqVJ2zQx9VTrADquzK/U0jKdUXSOYZcCVdbd2w8tX7GypuWBn37SsxOyvLKxdsbVME+6PnK+ckvWnUC7cd5OWMk6u3FnWk43s/1zLUbQxZfv4hIrdS8sDe35x0POwLDoFIgMFAK7Fj7EbIl7iZIh6IWMBcD4TqnMTJqASOrKw6Od4Q3pyxP4lHscSnrgoeTxxUUJ44uKto7zPCU5qtiaXJ5xql8G2RtEefTgKDcj6gqxrzUx9tyNTEMBmAD/bt2j7BoieHVdDBD52F96XCDDp0Q8G6x45MzQpFWBqOOnIrkQd66Zr602VHd4TvLBanAbm2nAllet9bbx620bVcen+l9tOauwzKzeXq/HLF9W/bjHirGPmfJj+Cq71OeVqSr23ZpsupSNJ2wybnBOzXEWbN3bVyjI9GQTwxaAe23SwXTA+HK3FIvwROYzBZlhYuV80JCBiJgAAvAG6exPm8nEogw2X/ood7BfYRV5ExbGNJy5KHk9clBCeuHjzKUs4wcl7rUnlCaeaE/hoe4IMB3MhKRbX2qvk5k2N6lZX2l+NsVKyefAjz6esG+/s0uq6nFaMED+QU0h77hT/lJ9cWmFtnKKlOaMUgFHHWQAA9UbHUbJ+irBaKLpbu+EVqJkMAMzszQV++mr7yZrD5YcnhrfcM64xxeKT5kMyMwDAwdFUuSt0ZfXOUG+qKikl651oqG1HY/X2XRBxJN0APjdclocRjVZDNIo7C8AsAMAcVGIWquHAxt+wAsZQlwcPQnJvwCw+H7XgAK1CG/sBNlGf5x45ZvHERckzpEWhh4fHIDhHZa8Tnr/BmHPCG8bJZUmnKqdS9mgIC9nmimxzZdsE9Y0NU9UtRcICVXHbXbg6O35ngzL3ojvqJ/7P+WW1WY2G+80GNItXnfXP9JJQmi/gjL4J0VgtClF++tBxJYlSNRPBbBOurHG9r60gLABgY7mW/t/xoR0A8LE9ySkz9oVngzn7A0oJhH92T0xuTlcYfn88lKnaFuTle11bBGH05Pfpc4X1jWi0zohGP2ZEo/cD+DNEK+pJENVAW7EeG/AMXgMD4VycgkZUD95lSsFh12M9PYmdcAF+Auqdu3Eyn7W/yZyHh8dbjGe5KCE8y8XRhTmc6jrt6nEt9gS/4YaOlqWigGpy3ZbJemOatqanTEoW5ss2l6buNCfXddkNDiPblmGZMlgiJGmVvU72qod6Nr1nZbZQVrsK4prfoMdirxW2EWluIohUzC9CFItK4xAsGdQ3toESY6aCWVm4is+t2bgCWjpdvI7icLrv5daTJvShdptWKV8z7YSOjCQP+N5F1Yy8rOH1alPO9pjMJZm4NUGytkaZ3cUsNLDb8Uf2K8yCqIIJHKSDLCQQzsBxqEQ5sjDwBFbCGvrk65yLOv55zIQOBVlY9AA2ssfQ9g7szEEAyAWYTbLMcfCiZ+8gSKm3z2Gf4p7looTxxEUJEWlu6oXI6R+MCeD1/GupQhAiikHEJRQmE6NMRQykXX1Mh11b32GPlx2uOIfRufSAO5qPr0gGWPe66dr6nMb2bzvSY5fN2G7OVi2uD5d1kvKRkvUxZdGqbMviX3anIr3uTgDf1mOx5uE+K99C/GQAV0CIjD6IQXwojiSx1rmngbgLV1K4luzkNVvWD7dqYzfKb3u17wNBx8QTVdH0XQ3TEwNWcBXfp+vXZS6u3hbocqWM65Li2PD7Mlya2mm6FSnXlq7Ev6l7lII3inKciuNAAF7FBuwa+n4+G0HnOsxFNQJw4NKLiLEfYytl3tLaFhIAZZiJA3AdMORkTc0xVbWZoliSoplM0W0may5JisMkspjCbJLhEuO8pLQFYFTolaf/x0teV9QSxhMX7wIizU1BiCfcUoIgbtY6RB8PHaKwUjlER8paiMZSNRC+/oJVR4YooJSBeJrPZ1i4cm2nUzWmw24IZN0wAFgymaPtWnowZAeK5HB5X628a+tEdVehI6lkczZ1tzmpvsMefzAxwwGWCrCwoVF7T5n01c6I/HRxVslw5EXGqQCuhEgf7YY4B/uh3obxlKxr7LdabHoVWmrYNFbqnDLzw/sS47+6b4PPJcLN4+f0vFpeLUQcZxJATK1ds+K+UPPJEdspy2SYDACWDLJlQh3Z3L+Wt0SvsF+VR3uGZTB8GPMRRhBpZPAUVsEceJ14OWT3Oszkc1ELAtCGlHQ71tMbGH1a7jCHj/7vnIb+hmUuhLgt1Njo4UA8oYYzO8om0+bK6frusgnVbYG6mh69IpyVfWZG9vOs7ENO0lxTUg1D1o2cpOU4MadomyXHidLK8x8OfNqzXJQwnrjwKHkizU0qhNAoiI5GALO0nDsjmHbLyxNuuc9ww37DdbQcz7nS0bNSFKOa3OdIZG5qVNfvL2rFOWq7nMqpu8yZis21g9XIKIiT3WOVrTvHKXEQVQJ4FcAd8Ybl7Qfbh0hzkwLgwwAuh+jx0QnAhKPIrOW4/gwRNRXntZvXDrsRIxRiHdMXEDONG3etLVvU1+HrVjTnK9NO7upWNNdvOKF6a2vHmL7ecL1uaZ+f3xtK2sx2eL9zwpI4q9C5/Oxmf3zO3ea6M17KxNlob0XjUYmFmA0CsA7bsBGtxYs5A9xLMI5/HFMgQ4IFh/6C7exB7KVD6EILIRx8+YkgBvtCu/QuAM0A9gLYA+Fy7DYkrfszZ/8+uK567lSIfitzIVqxOxCiIwMgi3d50zNPXJQ+nrjweNdgRKNhCGExD8AHHIaxrTWyumOcwtZN17Bqll4Zq1fCHIDLQKrJnUDWtST3yAaBQuOx3jKpY8MUdVPBDeLLutr0nebUij6n1pHIGqnSZgHV5Lojkb2xUV3XNbDiZi1E4ag7APz9YFYMAIg0N/kBnAfgEgAyeqI+lqqfCGZl4Sg+t2bza9CTQ90nHGDts06ApYfB7FyllWN3bXmtKmIZ0hpfyPpjIMICVhpMyiRtmXIug/u+aDrQFM2EenLMRlHsgMI4KSqXfrAzkqIWJC54LLHjw/9KdymHNvALJBDeh1moRgQOHDyFlUgMdIPxBShzrsEcVMIHF5x2oof9EBtoD4z9WwEC+QkQ1gIZwrqzE8BWCAHRmp/ieqy/aVp0iVEG4DgAiwCcBuGaZPAqhI6IJy5KH09ceJQc+WZVEQjzfxSiv8Q89A/CEkTsQXrwe3MK0cYpavCNKVp4xfG+6q0TlEpOBJdAfsO1fAa3R+P+Vi2uA8DOBnXznrFyC4jAHE7j91ljx++zphAHmeqBg0QL4qQvzLremKptKI7RKMKXP+YXIawY3cOsM4RIc1MEueCXKFlzDUAmsuWc1EyPW7tpzbBvSEcixamnQTMrf6B9d+jK1p1BBk5/C0acV8qldiJnfxqoRBxfPK43UqY5UtpiAwaUoOqweFZ2frS9IpFWJbk84RrnP57Y8ZF/pDr8xrABfyMcCPz4AE6ABIYY2vAytqJIpPAyyO41mMoXYCwAGRlw+j1i7DF0kQMbwDYA6wDsgLBIxPRYbMj3o0B0iVGJ/rTZ4/KzXYigWU9MHARPXJQ+nrh4F2BEo/UQg2wpQQD8EP0tyiBMz7UQrbTHoL/jpQQR2JmCMEePiqxGbPUsPbxyjlbxynxfbUeVHAAH9JxrB/It0YejULsiGWTdGxu1TekAy+ZdIJHGPeY0zeQ+K/9kf6DPl22uMhfS7qiyZVeDEjtIq3TKn4MsRBv0Fw/FihFdYlzuVuy81Dr+d5U81FbDQ22roaVbh6zIiVjLcYuYQ2pVtpuN7ev0B3JZBQA+nEmwUzJJ2WHcub861NmsKgMEUH3Ali+f0xNJmsxxBkQnclRorryi1Zf6vz3BVEYjOeNnSiDjWh99LrXr408nWyO97qHXqzge4zAVEwFwrMVWbEICwv1DnMD5+xB0r0ENIrCgIQPCOui4KRiO7TiE8xQEcAqAj0K0aQfEue7Fu9jFcTh44qL08cRFCWFEowfKFlkF4KilUR4jFLJDAGGRsCCO0cCbFAi3K6ro/zzJV/XPhf76vWOEC2Ww0FBNrnMC3zlO3bx3jNwKIpT3OcEpu82pobRb6TCybPnALpB8RoluKmRsmKqtK05VPQT8EFaMxwHcGW9YnhlpxegSowrAHwHEOXil0/h8q9V0ux8iALgD6N9PX2fV+LpWdc6YZJssuS45jHGbyS4IUBzOvty9T22wM3Zclpw7ayu6smxgFEVTNB143zDuEQaOct2V/7Al1LOpW88BohR62s9U5oK/57VM7FNPJGJTd1sjHkfhtAEIQUEY78V4VCIIII0VeAh78RyEVWKfvR2VAL4B4cYoZBf9FsBvg3pswG8kusQgALMBnA3gDAh3SQbC8uXdPA8TT1yUPp64KCGMaNSrc/EW0lItqc8vClQ9/d5AQ0uNHJRcSGUJB4bO2jZNVrdkfSwXSLu+yXvNCVU9zphD6ZQK7A/aVNqr5OYtE9XttkKHk7HCINxCrQBuiDcs3z7cStElxlcBnAtRtGoMgM9l//vMfQA+BeBicM4jPU6uocUZH+7RJwOAKUkOHyQcOJfksW534stdHSGdc1rn07K/qwz3FVtaJOK4fE5vpFJ3pNQg94gquaQy0D3rKuLdhrT/eG0GSoQkzWWgGdvN+MefTu49/bVMTz4ugyDiJMLoz9TYBuBlAOtxNvowFT+AcBklAVylL461A/vbt58OITIqIH437QB+CuCF6bduD0KIiU9DZBw5EL8fr+rnUcATF6WPJy5KCE9cvG3oO6PKmMffH3Dv/1S5Ea+QmGZyatxthmvjzhgOwDqETqkFa4UlU27zZHVDZ0TuOdD6h0glRNbDzwA8WuwmiS4x6gD8AcJCUQXghdhS/SZABL8+v9D/iUfODF67bYJa70vJjJlBhcgdInQ4ZxKRbcpyouekVFY/rzdZDhD+Wh7oWxH0D3BF1fqFeyRjM8d2B7p4QoojxQ3Zvu+N8rg1aJlLQDrFphMAACAASURBVCLINJeRXNnn8I/+PdnxH//K9FX1ONsg4kxWA9ikx2JDrBvGsugJAG4AoAKIAfiWvjjWDQApIxoGcBmAcwAww9LkzR0zrO8/e4O0vnWuBeHyGDH2wuPw8MRF6eOJixLCExdvORJEjIMB4F4AT3SXsap/LfAvfmW+7xNrZ2hltkRWIOPmNIsf0PpQsFZ0VkqxzZO17ZZCR/MJWYN4+n4RwK3xhuUJAIguMa6HeDrvAFCn2rmLNz40KwARU/AhALJL6Pvbe8rDv/jk2IVZv4Nwgmxp4MBPnDMmy4k4kW2Dc5zfnSyblzV8JhG/t7o83qIqA47l5LqM7+wJ6XB3jjnAkPgL6d/teuavu0L9FUvz6bccgCOR1R6ReturZSvlZylboWcg3D/r4g3LRzzHxrL9lorFEPVRNgH4nr441gsA97543Udn1m24RZeNBiIXErnW2pa5bQ+8etn2Xd2TRh2r43FgPHFR+njiooTwxMVbhgQxWHMAfwXwIITI+BSA9+fnd8TqZPnRM4L1T783MC7tY4puDA0CLY6t2DpR3dhRdVSsFcNBEG6SOIDrffc/5QL4JYDW6kzHmM9s+l3zlWvuLoglDlH/wgGA9ZHZM2IVFWOf/1CftHKB6VdN8GBauDU4ZxJjuYwkpfeLAd116cqO3kiVbctdsmTfXV0Rz0jFbhSOi2b0lU8IW1rClAYIAsoHeD6yKZje3KnbAJDxsURHpdQWr5C6+0IsXeRqkSAsLhKEheEvEKm4+0Y6CXmRcSaAL3IOuYtXZS/I/K5jpzt5pkS2+Z+zH5XPn/+HKX41rQKAwyX++t6TWv6w6oI9O+JTDhbz4XGIeOKi9PHERQnhiYs3HQYhKgjiaflhAA0ALoLo4mlDDMoDbpo5hejJpkD1n84OTWqvkgOyzd2ypJvTLK6Dg/bVyTt3jFP3OPJb0ii8Ahya/4X/Tpz6fPWY/9zxeHBKz9b6Kb3bN+tOrgODXAA9WnlobfXcBapjGgD47vG28v8+kQ53VblKMMEcxWakyL1dIHfAvo8xLfmKzt6IykGbdMX4TaSs1y2KvwgpDvvKvJ4ql4PnHMYBELlg4IAicag6t29uj6x9PeBrHSH1djA+iNgJgrBK/BXAiuFScqNLDJJhzTpP+cvSc5RH36vA5i5Y9vvGt9e84c5JhbQ+6YITfjvuw9Ofmigzi3FOnIOwOnZ82+9WXbhrW+c0T2QcIZ64KH08cVFCeOLiTUOFyL4AgCcBPAVR2+ATEAOaAVFw6YC4BLxwkq/iT2eFp24fr0RyKiVaa+TVqaD01vj0OUek1ymr7JSnMJdNXPSaa3z0Mb8VNsw9M7s3bxqyOoCVdSedlJV8QcW19gei2hLHC6cb/uc/YJZBMjIVKaNvuFati1IZ30d702UAx3OhQPK5ssCA45xWntMvmJao6M0ylxNxV0PO1chwFZgh5ihpzqwvJepf7ebSaFxEBBHgWSiItRpCCK6MNyxPRJcY4yGauS0CkCO48dOkF8u/ot01W4HFbEj8z9Yntz9mndNaXdapfvaEX09YNOGlsYxcAoHAiW9sn9n11zfO3btiz6Iel3vj4OHgiYvSxxMXJYQnLo46ofyUA/AYRKnn90B0GwVEC/HR+OM1CDN+/LfnhP/3m9+sngWi0yAsHh14M1IbOUdZ0g3Wddk1NV3OGNnmmuMEwoai8J4KzqrbFff7d+56fmoslRj81n3BMbVby6fO0ZzckCd1m8lqssyw/n7unuSaWVqNL+tawSwfaGHIx1/MzRo+hwi/iYS7t2qapdhcAwdxgnvGcWl7QV3W30VycnDjz0py9K2O2rM4WbvGwmH1NSUI8afBkWXWPpNLW84sl1qP66FMVQsGne+pbIv/69rts6so7uMAtrlTe36Wu2oLhTk+Nf/3406f9K8GmTnk5ut09GXLjSc2fWT3U5vOau8zyo9WjAyDiAmR8pOcfy0l6ERp5Qc8cVHaeOKihPDExVFBhrBSSBDpmS9DPAmfDmHBsCDO42h+OAwilsEC8ACAR/WYqKcQaW5qBHApRNloC8KtcmQ/Ss4RTrn+2i6nprbLHluoEmpLZFqkKY4TLCdybJeTlCrPmZprpG64q2vNwjVGX2ETFpOlFfULTyXOwfjQIlY5SfPPjr/xesTo6v3XAl/FXRdWzOgul3zhpJNT7X63kOq69KXO3so601azjOEXleV92yNqa1u13NpZKfXqEsd9Za0nh8nRk1walKbLUc0c/9O54O47MpFhU2kPissY9UXHIVU1EUpWhZK1QRyUrk6xlrltUtucbupqTBHvbxkfRFK6SP31uPfLzzcwuGRD4o/bH931knZK19nzHh/73sZ/NCjMFr4ccNhc5mtix7c9v/39ba/tWdhjOtrBrl+hyZ4fwoVWOF+Fgm+F6rFpAAmIAnAllQK7VL/xhgvU3+vDLErqi2Plb/kOeRx1PHFRQnji4rBhECmbKkQQ42aIwmMzIKwNLg6vxkEhRoMhH/ipx2LDuk/yIuMyCHN9BofgZhkA5yhPuKGauF1VE3fGFAkKy5EK+01kWeVVJJ7oOQcxWe7tzPi5ZGhMvuzh3o2ffDLZyjiwpWLqpNZA/UTVMYdYZixJ0cO5RNf8zjXrCvOyGrHfnBeOPvLh0GRbJirvc3KqDUl2uFJhO+wLfb0+nbgdC8rdl59avzKlsP2BnDOkXGBZqP3kDGeWiYE1PRg4RZjjuztTsf7RXPigjdn6zweATGUl6x03A46iQ7JzgIgL4eCAbCiQTRkgDld2WNeULtYyt5N1Tu9jqdocABBcHC+tCn9R/fmMSurWASAH1XkY52/TJ2ekD896anxVIO4vjlQ1bc19de/JLcu3v7997b55CctVdQjrV6EbrwRhpdoOERsSg7jW8fxrJrZU927KHu94PHFRQnjiYlRoEO3ZJYgnyDaIm3+hg6ULcbM/nA6pDKILqwTgGQC/0WOx5oO9KdLcRBBlpa8EMA3iCXbEypzM4RTpdcqqup2qqh6nXrG5CgwWFP04rs/vOr4QketwziQmZZMSy2YAwJTBesOSfsZL6T1f/lVu39rIiQsV18oNuUEQyGSqfkL7v18JWakh7pK2Ksn/4MfLZv1job/aZchmdLatvVruPLU7E7x+ffd8xjm9WuVr/daJ1W/wogDPj2mJuiv8PbPjrpThg/wjKrgUIFe5LlWzco2tH7xSqaXr1DNhKhmhGjDHAjkHvIacbAY1q4BcBgIoF8xR15QuqX1WnLqmJChVndNg0YfkZ2ouVH8zVYHFAMCC7P67+oSOypld+vT6zREilxxXIs5J4SBuOwq2xxtbtnZOe3lT+8xnVu49eTWAWGyp7vUe8Sh5PHFRQnji4oDoEH1IghDCQoKIl1AgzM8cwvycxOG7JST0i4q/A3hIj8X2jnYjkeYmBuBUCJFRC9HeOwcAWs5Vqrqdippup7Ys4VSRGInJlsl0GUas88A5Y7ZdXkXgHABxgCtKbxfQfwNwCNRdIfkmbQmw//p9lRNOO0OsFqak+moyHc0zuzdtHbSoAsLUbwJ48vbLKt/4yaUVHwHR8RDntffKjd0TP7Yn2cgB/v/Gh7bfNbNyd+HNBI4bA13TT1GzY+OuNORzg+QqNuBelah7LeYqww/OnIj6xjZQsq4RAMBsY7SXkoMDkiVBMRSAAwSCpZusZ3wPdU7rlnompgLdtZkP4KXIBervpqgwZRuSwhVQb125rU7LZSdGd1oBLZ30K5mkLDmFVuuAELCrAayFKEW+J6jHzFHtoIfHOwRPXJQQnrgAIFwbQQhTtB/i2IP5VwfC5ZCGGKxT+elIU0A1iDgNF8JS8bAei+0+wm0i0tykajn3PNXkVwczbvm4fZYWMHiAA+AE15bJPFjVzwKOEwi7ruYTVgtJlqRUL2O5Ib1mHFdRu0P+qkiccpc+EOyp6JX2nxtOxBySlAVtr72oOzkLQphVoT/9808AXimKJyEAJ0KIpAmSy3t//Fr75Dk9uWpOwI9mVq59fFyos7B9P1x2b1nrgkpyfIkh8RdAOTlaF5eyVybqXu8bnEGSCwZY98RZsPQwJNsouECOFA4OMJtBzimQHAZOHOCMMlUO9YzLKPFxqVPTzduvzj7qzHR3lelkOtwPxY0iiMlweT00qMiCwQHBzp8rCeK7yCA6sO5Gvu8JhADpQT7mIqjHDsdy5uHxtuOJixLiIOJiDw7PxH8sw9AfTS/nJ4JIDc1AWCYciKC4RNHfR4tCNkkWYmD9mx6LdR3JBo1oVAIwEaJZ1qkA5rVVSfovPl0+9oWT/GHZ5mYo7ZqjafvOuSzbdjhC5LqcMyJyXVnuHWY/iWy7LMI5sUSZQ7pB/JJfBbvH7pNtQFgtGhJ7t01O7OqFEGwmRCzJE3ostmukz480N0kA3gvgy2WmU/vzl9vG1Wdtn8XI+eaJNStXR/pdHVMk0/+TUNvJBic7BzbkWkXI8W13lJ5rkrWrTTAOl4j6GsZTqmYywF0w+01yORDgSirAJA6Xc193LwJdCWipHBg3Ib6DubDpxD7anDIu2tE3ri5rV2hwHS0CRapFgI9BBcoAKOiDiixkZMD2/yZVCHHqiA8DK2wTJRjQ+VA2/NEbUzXKMIuS8YblXkBnCeCJixLiIOJiCw6j5fgxjg0xwJkQgiKXf30zv9QyhOuDIJ40Hwbw3HA9LQ4FIxpVIMTENIhgzhMgLAIM4nolkBdEK+bpZXdeXDG9pVoOlg3KyjgQtl1WybmkFKwWspToJmYNMce7ji/guL5goX9IOuAyWwJ9+neBnhmbVLfMTKgz4ps2S3B3Q3QRfUGPxQ75OxVpbtIA/MeEpPmVH7/WMT9sOTylsOyXFta9ti/Q7+o4S01WXxPonht3paw7JAWVo4o5/hWWr2VJfOIeik+eDVsLQrJyAD/6Rcg4k8BlFQCgZHp5sKOZ+7u7wJzhPkuGcA35IK6hI7mcT0xZgUUdWf8ZLWl/nWmxQIDDH3LJV8kVuZxrkg8KhAXKhoIMSbBAMIkhSwwmCA4O0UL1DoFWu9op5yYbhk1FjTcs91JRSwBPXJQQnlvkTYMggj99EILmaYjCTJv1WGxUPyAjGi0H0AghJk6GqOxZeFLNQQRxjviUasqgX59XFv3jR0JTOAgVCcc4kBXDdVXNcUIVRI5d3GBs8HqcS5Jtl1URuAvqvymYisNyPkf+xCOyeeqr0iOz4xvuAPDGaI+7mEhzk//CHX1f/OyOvuuIQ97nl7uvXFg3IIPkm/6uKR/Q0uO7XCmDQQGeBI4yVyr/bfsMPByfnH1TrBVcVsGZBLJNHog380BnG9TsEDfSKGAQ7jMVgBKwXL0hbWlTEqY+KWVq03NmsIHbPk1zZVkBk1QOWQWTVE6yyolGY6p6B9BrSvr7I+OHsyJ64qJE8MRFCeGJi6MKASiDqPTIIYLwngDwsh6LpQ5lA0Y0GgYwAcB4APMBzIPIRimkJBYCSEf9xL0rqui3X1Y5Y1OjGgmm3ZwvN1xjNCLbKq/iABE45yhqMDYI2w5XcC6rRK4DDiiuzZjrki1JPFYeMVtrJNOq7Pg6mPOb4s6qR8K+O8ed6zD6QVyVal6v0pM3HF+92mKUAQAFnH4Saps/SbbKe1xp/6DucsayuVAZdyStVs3g7vZpvX9PjD2SQb8IIriyBhBBzva54dbd8HfHi8XWWw1xTrrDJcYxXBHUdyw5iT5ms2HL3XviokTwxEUJ4YmLI0ZFf3oqAGyAsFC8NlJ9CgAwolEZQD2AKIBxEOmkM9Gf1ipBuG5SEG6bo4JLwGNnBGvu+1T5jJwKqbLPHWDFKHZzcM4kYqYhS6m+IdvJWzckbjmKazNwIKEHzH1l1Zluf9jkruZzq7augb/PB+DPAO4+UAfSQyXfROxLDvCZbk2q+N8JIff7x0W6OFECQCpCtnJ3uG1BgFwlySXTslUtmwuVcYAYuY5KDipkU7qjdVbvy/naFIcHEVxZBwCu97XyUFsztOSQiqEeR5XzMbyo9sRFieCJixLCExejRoEIyPRB3OgyAF6CaE2+Xo/F9rsPjGiUIIIY6yG6i44FMBXCxRFF/3kvpLgWMlLedNojknLb5ZXTV8/Sa0MpN6eb3MmnnlZTPg6hUDCLBjUYAydGuUAN4xy2xNzWcCTdEaw0soomxIOr6FxLdfHqzetAYPnjfhbAD+INy484jdJYFpUA3ALgFAdg/xcNvHT5KfUTIYqPpWdIOWtZqP3kHjOgJcygj4i7VJQJopFDYclit7bO6fl3umqU+0MEV9EBzrm/u5mHW/ZCMbwaFG8NnrgocTxxUUJ44uKAqBCpqX70n6MMgDUAXoewUnRD1GuozL+OATAJYkAdA+EzL6QQFmIkClkpb+sPySXg0Q8Ga//n0+UzbIlYOO7TOFf14QpmAYDsQJEcLjuu5ovr1aytrDzR4w+ZAwtYEYMrq27thlegZguBmwRxPl4HcGO8YfkhuYgOhLEs6gfwU4g4FDIY3Tr5E5NTAC6EI89cZPoav1G5pyJua5YzTI8RH7PJzxz23X1zu9/IVhxCRlSxqIjnRUXOExVvLYctLojoEgC/Kpo1kXO+O7/sfQD+AuA2zvmtR2dXPQ4HT1yUEO9ScVGoG1BIR/WhP3CO55crEO6Idog6AmmIoMlCI7EKiPiKwX0egIFZKEczjfVNIVYnazdfXj9/48RgtCwJU7YYA4Ercm8XczkrVPHM6CzZEgnE2/lxEy0F2eJiWvtxVR8PdOzilXt2DvNR9RCN3L4Rb1h+6GW5R8BYFq0E8HMIqxAAXDs5tdl0q7b+2Gl8bvwnpz0d+WS4xddh+S1wNmRfA8wilXF2Y2xe91ajbASBQci7P4j743t5WcseyDmviNXbwxFbLojoQQAXY6C4+BREBte9nPMvHp1d9TgcPHFRQhxEXHSPsOydChVNLsSxORCxDVkIQWBC1PbI5dcpWBzcomWFyUYJnB+bJPZq3UmLXj7FCv7f2Wm/YhKrSqXSRLZly5Rrr5L3tdZI7Um/nGVtcxbAUfzDZltwSQY4d+vXvQxRZXI4qiGE2rXxhuXbjnTfjWXRKIB7OUeojddWfjlzj7HOndsGIImyvfq1Z1130ryaLTVtjuKSyzhxyS22s4SYxUDAjbH53TtzoYFBq66sgTPG9UQ7L9+7o8gS4/H28KaIi/z8egDtnL8Jqckeh4wnLkqIg4iLFyAq/5USNvr7gHhfZADbyhsndviqJ0eMbnfPWEl/4BJL2jnZbM3obHtvGetFPqeRehvGU6JuCiRz+PocjurnlbvX8WBnx0E+shzCMvSdeMPyV490/zf/8NTjOOgvSR6MEGAsMZauXOfOTQKArmTYbR/92vFjqrZWtTBXsWVTJg6QK7mUd5eEJZNxEG6Kzevengvb4JIMV1KhZnvd8r1boSeGtJb3eFt408SFx7FBSaU3eRyQQtXKUppMCHHhCQvAn5W0CYasT/M5hv2PhqZ9/zPxu9u2Nn/3pJY65d7ecikIIj8AIBfwU7J2MiRr+MwVV9agZHt54KDCAgB6Ia7FDyPNTefmS34fFtElRvUZ6eeuuslY0qeRmZPJwhL9puOns00BADAsv7v0qZvXppNjElEjnCrrGxvXcqEMZy5zJFtymcP6HNUFgO9GV0emqpkgwDmv3L3WrX3jdU9YlDZEtJyIeH5aXjR/YdF8TkRNRPR1ItpLRCkiep6Ijsuv20REK4koS0TbieizI3yWTERfJaI1+XV7iehZIjrjLTrcYx5PXHh4vDMp1OEYA6CeA9aDsy5N3XDq9zaff/bDy5eddG1ybc28Bzdde/rmeMPyHwG4HoAOjmrWPXEmAD58RUsigDG3Ys+WUaRipgF0AlgM4JpIc9NwZZ0PSHSJMQPALwFMeMk5ffP/5C7bIMFhKpny9/QbTpjMtvsAoDtTZd301PdW267ihplN/nRNsqJnQkcwVdsr25rlMlvq4UwyObFbJr6knDhuxQYe7Oz00kpLH855E+d8yJXmnK/Iz1+an/VNCFfoXACnQVTIfZaIFgL4FIDzILLAdgD4NRGdWLw9ImIAHgHwIwAPQLgHZ0LEID1DRBe9CYf3jsMTFx4e7xwUiBtZPfoDKu8EcMn0Szffs+ykr+tvVM3Z7TLJD1FT4zeFN8Yblr8I4PPU28C4nK3hbITsCFfWua9nH/TkwVubD8SEKId+LoBlkeamikN9Y3SJcQaAeyCCaDsA4DH7vLaHzIs3ynDIRxnlZv3bJ4yjPToA7O6ZmL3l799ZrUi2pMmGBM64mgvmAn0NCX+8MR02wl1MzbZbkmldH+5YsEjJ1I/yWDxKmzTn/Kec8x7O+RqI31ANhFC4knMe45zvA/BtCBF/waD3fxnAfwL4Hef8Z5zzFOe8BcAXIHo43UVElW/Z0RyjeOLCw+PYpWCdGAshJgIA/gnxBHaOHot9UY/FHmn8/PYeh8mLIYJ2AZFK+6PYUn2AG8B3/1Ou9tidYO2zm+Hv83NmDfz9cyaBuMPL9+44zP11AcQgmq7dF2lumnyglaNLDIouMS4EsAQiHmhAga8/Wp9uedg8f4sEl0KU1G71XXdCA+3VAWBty/zEnS9ctS6oplVFMpnlKLrjSnJjefP606u3/fM0LfXiTNl8sYKc3TcGuma+V0lPhziPocM8No/S4YlBfxeCkVdyzosDgbfmX6cOWr+QhXJ/8UzOuQNRZC4E4ONHYT/f0XjiwsPj2IEgbkxjIFIy6yDacd8F4DIAH9FjsZv1WGy5HosVD8T/DVHgKwNh2VgN4B/FG44uMQjA18nWoay4fL287uMboGZVrqTV/Su5ssbD+7ZANo+0e25bfn9+EWluOn24FaJLDAXCjfIFAK0YoXLpr62Lmh+zztkuwaUw9Wk/9H3jxAlslw8Ant/2wa57X/niVr+SCVf4uvtObFj5ckNFcyuRcO6EmZuZINubZ8jmK78It1k3BTpXEng3xPkdC5GC7N0D3320Dvo7Odx8znlBnPsL84goCGBG/s+1w2y7Of964jDL3lV4P6y3ACJ6sCiYaPfbvT8exwwM/ZaJOgjrRDuABwF8DcBZeiz2ZT0W+7Mei23XY7EhMRLRJcZ8CFdEG/rbzy+LLdUHB7meBWABgHYCg7ztw63qi1evJFe1uZ7QuStpULJ9PNQ2+MZ7uHRDuGZuiTQ3XVEchxFdYvgB3AxhWt6HAzRq42D4hXn57qesM3fJcFiQktpt+jdPbGTb/ABqn9z40dSWjunLZte/0eFXs8OmzBIh42O8+VJ/38m7q3e8XEHOpwHcAWAzhDm8cO59R+nYPY5tRirBP9L84jiOsqL/9w4KFOUAfpZfVnukO/lOR367d+DdAOf8EgCXeMLiXY8P4oleRf+AuhHAivzrVj0WSx/qxvKD9Lch2rK7EAPkA7Gl+t5B640FcDVE0OV+WOe0pPr89a+Zi34+l4faqtxQ28qjHPiYgagx8hkAsyLNTUt99z8FAD+ACJiLHcpGOBh+Zl61g8GlDynPTNApqy3RbzrtB8Z1f9ngzr7+wgV3dqaMv2yD8IW3YPhiZ2Z+2WfXVO2qBXBbUI/9LdLcpEO4cRYCeA+EVYNDnM8+HMVeMB4lQW/+lQPQOedeEbYR8MSFh8ebgw8iRqK4ZHgHhLtiDYDtAHbpsdiRuCAug6gw2gLxRNUGUZ1wP9ElhgwhQIBhBkrKVJnq8m+2mE0/XMurdtRCDMJH84bpQIiImbC03zt161yp7Tglv8+HDAfDT8yrt6fh931EebxhIu3e+5fAufWMEAZinQD+CGG+vhTCGjJcDYXCvnwAQHXKiN4Qb4j1QpQyfx3AXZHmpkLk/0kAFqFfbBCEJSY1wrY93gVwztNEtAHALIgmhdsHr5MvQR7jnB9xYbl3Mp648PA4Mop7lgBiAJMh/LerAKyDiCDfqcdiR63OQnSJMQ8iaKwF/bEaN8SW6oOzQP4LoktrM4YnSI7arb785YuMiS9+CMLCkYAYRI8euWCKeqMLrIX3au7292+UN5xLxOXR1CdhHKz+PvMLb5ylPPnrOqn9HAA6gLuMZdFvBBfH1qeM6K8gRN2nIQTGcBYMnl82C8D9KSN6fVCPFQL3EG9Y3gkRNPvPfM2OKggryywIP3ohuK9g40nnp2O+NLzHUeMeAHcDuATAd4oXENEJAJ4H8F70B4q+Kyk5cUGiUNBFAD4G8QRSA/FE9ySAGznnHUXrXoKBDXDmQTwNngsRGLcHot/BT3i+lCkR3QQR3V5gLIDbAHwI4ulxC4A7OOe/wSggokUQT5inQAxUOwD8DsAyzrnXVOntRYGwQOjot0RwiN9PAiKqfAOAnRCDeEyPxYavfHkUKHKHJNHvDnk2tlRfNWi9RoiAybYRNkUQFTav2/et+gyw/NFIc9MeALdCZJyM2GZ+VBjhMOuaMh8cnEtSypn6zFS3eltEee3zG1m65lC+2zrE7/ExDnb3bGmjAXGevwxxLX5qLIveEFwceyllRO+BOCefwcguEkCck3IA96aM6G0AngnqsQFiJ96wnEO4kjoBvALg/nzsSAOACQCmQ7hUpkB8FzhEzIsDUYLegLACeUXeSot7Iaxf1xJRL4S1sA9CUNwD4EHO+b/exv07Jii58t/5gicrAfwEwO0QPrL5EEozCOD4oijgwnsehCgjuxHii/MQxA3tBgBfAfAzzvlXB71nOcSXaXX+cx4DEIEorPIJAF/jnP940Ht2AwDnfMKg+ecD+C2AZwB8CSKo71yIokIvAjjzUOrkv0sblx0JBDEoKBAWiMJUKCleaIqWghio9kIIiRYIy0SbHosd3Sf8QyC6xLgKwmqxD0KIagA+G1uqx4vW0SC+P9UY+brXQrgDvlUcABppbpoAEfBYAfFdPHwy5eUsPnk+iLsgxwIADg7oSR2O6iirPrteip10IBFTCXF9boMQUPv301gW/TiEpSUF4YK6Q18cp07dCwAAIABJREFU+2vKiBKAz0E8WbbiAAGj6BcujwC4J6jHRu0SKrJwFLrnToYQHFGIe4KLfteYlP/bQn9/Gxsl0ttmFBzNrqiAeBDcDXFPLmYpRID0rsHrc84nFN3Hi5kI4CaIMaGYSznnD+b3QQJwOYDPQ2SP5CAsFfcB+KXX16Q0xcVMCMvBWYPmz4XwdX+dc75s0LIHIb5Iv+acX1w0nwC8BmEOPZlz/lrRsuUQX8rvcs6XFM3XIJ5gqwBM5pzHipbtBgaKCyKqg/DbuQDGcc57i5Z9F0LgfIFzft/Bjv0g4uJViKfsUoIGTWyYqXAzH9x/pHADS0GclzhETEQbRM2FXogn926IAWDw5w73Nx3CvEP9e/D/AYB+PfPCqU9NOPMbmpPrJM5hSmr1wtYV931lzd2rit934ylLz2sONXxQt41OAifK/84JHMQ5cSLVJtn/pbX33HJc1/reQZ/HVs3SQlffUPv5njCLBjI8zsRbC9so+j8G/h/Yf5a5FQi72drxINcliOZn+w+Ec5iqzSzdVqatrus66fnxXWq+7AZxF8Q55WQ97LOzqQ/tfubxSYldXRDXc/8+AgCOx1TMwxlwYEOGhh34N5bjdU6A+03M4x/GQiSQhFM0kPEh14+hHEG0oEv6Pv5Fm5HG8Nd4uHDXA87PKcSa62VfrF72t1XJvt6wpLVXSf7OSinQXSb5UwHmM3SmGCopLgNjHJxc8MJJpP3/ls59moNgqBgXG6sOZ1U65N4iHsc2JScuRiJfstUB8BfO+ccGLXsQQlyczTl/ctCyawH8EMDdnPOvFM1fDiEuZnHONw56z90QFohrOed3FM3fDQwRF9+AeCr7Fef8c4O2MxPC3P4y5/zUgx3jQcRFJ0orEI0XvRaEQ6Ez6kiTW/T/QtOzw/3c0eRVHOqPbKRtcgBkkSRtrZw20wUxmTu2xRQ1YKX6JvXt2ln8xj41HNoTHj9FcS1TmAmGfrzFFK0+3bq32oiPZDWgtI/Y975SNf7fs7Wy6riTkwZuZuC+DvoIziXF4b5AvsT4iMfvMKCnAlJNB5yLf8fSDfvI5kTMIkUNWcmeccnmPTIf0pV14PYaEMJpaIQLDhkSmhHHy9jNHbjuZ1DLz8c49CBHVtH7aMgGOcqhggP0AHaxJxEnXrx4VBzWTTWngJJBSTI0YjmVmKkQmQoxSyZyWWkVMG+plk798s31R9S4zOPYpuRiLgCAiE4D8A2I2vFj0f+UCghT70jsHWbelvzrvKP4nmIW5F/XDLOsEIR3PBGxIzS1rYHnFnnHwgFsjMya3aNXcNUxUy4x6f+3995hcp3l3f/nPmfKme1VddR7teWGsQGLlhBeIIApDg7ExJSX14FAAkkgwHp/8JK8BBNqqAktgIMhBGOMTRU2xVWSJatZXTuq2/vU8/z+eM5oR6vd1exq1Eb357rONbtnTnmmned77uqL4y/p2b1RrEkWgOGQF93SvHY5MOj6uTHdARk37FVkhtqbkp3bJjpn5bDhI59sP/zxtzcs/vmNlfMaenPDodyZJ07fj0RzuapqMJmTJpMJqO4jd6LJd/7pb6l8/i9jQzc+VJ2d35vYtqDvwMGiZtQ2TvArTvB8rgJc5lJDHfPk12xxv01HLke3eRMrTT8pSY0tKAVggLSJ4Jq/Yp5/I55zFzul8zSr1TkjmoFo9+URF/rIFd6FHoJyjim7IloicivwEDaQ89VApTFGChraTHS9Gst/nq87UDvGcxhjJr3PKPLbfHqMgix5N4YH1BRxLKVMSVTFZ3R5DTMiufQwWMvDwt59O2LZ5Elh4SOyrXHVKl8cdzxhYawFj+VdO7cVM3GHc5j3f6Fr9+t/0r+7u9aNpUMTXzMCYVEHxi9GWOSpHnD8qj7X/PJFyaqv33EwnW1ItE/qVv04/TzIY6RIAT41VPFSrmM61e7dHHE+yWZihE0lEzZVkzQ5Ohgya2jOfYHr/Zu47HtEKMpUKDtxgc3kEGycwpOTzLSoGmNdZfDYO8Zz+XKwk9pnFPkYi7fmRdA4S8+ER1HKloFwZWxf3cIVYT+TAmt5qE33ts8eOHxKsOW+2oVz+8PVDeHcOK3UgbQT8eb0t+2pzgwMF3t+x8A7vtNz8H9/u2dbX7UbTUZkTLP1VIUFgDGOG/IxzX2D7cen50J3tE6//su31M5NhaV4jdHNMD/lMXroRXBxcHkR17KUac4v6HA/zBMYMLVEJzqMGJBukgji/z3rch9ltZk58T6KopxKOYqL+cHjKTnGIlJMad+5Y6xbHjxuKuE+hTwaPM4f60kRWSoi64s4jlKG5MSR7Y0rVwM4xs/54rhijL+ia8fOwlm302uoTVTHF0f89LjCIuuEohXZob75vQfGq3kxIa+/v//o33+xc/NQzAkPxuQUC8CUhYVBjHFDItl0yO3tdCSbrev3U9WDufR3X1az5C8/PuO6jauixTcbGyTDA2ziEAlChMiR43rWcgOLZSv97vt4jD5Spp7T6qOPRobJ0smwuZJpuS9wQ+4NzDZuecU+KMq5ouwCOkVkDzYV7HpjzKMF61+MTfX8jTFm/ah9vo4N6PyWMeZNBesFm9Z6FXCdMeaJguc2YAM6P2KM+XDB+ny2SCM2W+RwwXMH4LSAzmnYmhYdwJLCrnxButOTwMbRwZ5jcYaAzl3Y3PtyIX+RLwwYzP9dmB2S4/RMkfGONdXni9luvOcmCuLkaMX06Z2xxumRXCZlsO6QWYNHDzakuk9asjLiunvqFy8zOI5jxnKHCAaRrOOGF/Xs21mRG04y8fsx4UXhyVXRyta/blpsQGoH/IxvQmE/V1GN+Gd6n8c4k+OKk0m6Mjw0RpAlfVVOOB0R5082DB5/y/d6jlYNnYw7OvNnsoomrmAOWXzCuPQwyMMcMCF8/0MsMIuoooOUFBHJZCI41BKWBMPOl0nIU4xXpn3CcQWfYSjjhMMZJxTOOSE3K6FQ1gmF7eKGfXEcg+PYR3H8wJVVLghwcGa07i1fHdBskTKmHAM6/xXbRfIrIvIW4GlsKd8vFrHvTBF5JzYvOop1sVwN/GuhsBjFOhH5M+B/sILiX7G57u8uFBbjYYw5ISJvBr4L3Csi78daXeYDH8EGoLaMf4Si8ShPS1WewuyR0emcgs0OSWMLGw1h42L6sIWohoP/hwqW0ROlKVhGU7jtWNvkxU7hsUb/f9q5NsRvmn//gpfeHvHTT4sxuWTIq28eat/63ic+cXd++4yE+Ofr/uGNXbGG6kgu3ZXPsrTJp4IRm3yaCkWbl3Tv/smazk//fNT5Rr8uc6bl6m0pc/MD/dPvur3hb9JSMd1tnz9LHNOF+LlR2aj5sRS+ruA5x8EPRanoOEjVkTbklAA/u52c/Mf9zG31TZ9/Y/3w2p2pL//n3xx5LJYy4302I+u3YVjJWmbwj4BLA7CQnHTzcedbbMx9idtZwp8an3ZGgmLHzSgBMEtpyL0QjyxPsouvhW5m3+htTsSazfuf+0/TDtTMnzEcjs1IOdEFWSe0yBdnji9OA5ARbE8Kg7iACCZf7yKfyWS/M4acUH41E4ZnPfMa+IcLPQzlHFJ2lgs4WZTqb7HuCYMtFPRPWMtFnsKCKF/HWi6WYqt7vhFb9fAQtvjWp82oN6rAclETHPtmbMGfXcDHjTH/WbBt/viFfCNoaJbf5lps1cXnYgsjJYCfAv+vGJECWkTrDDhYMZ1fwsESYsS6kd9OsLUu8oWzDmCLSZ2sg+ElEuf0hxNvSTYD/xGMpQ8b+JsEbku0ev0F2/05tphPgvGtBs1Ya9odiVZvooJSk2Lmv//6huySX37P1Bz2SFYPSLEGHuOG8N2wqWvbbmom1YW1Gvs+PAl8qnPOhoPF7JS8Kz4LW0xpKVZM1gJ3m2q+mnsTNwF/jxWe3UWOQ7Dvacg38ovPPPTuB7/4+zsqsYWzrgjOE8Z+p/LfL63YWUBu+tZb0i9/n6ailjFlKS4mS8Hkv8AYc6DIfTYANxVkoVxwVFyUDMFW6owGS2HVzhC2qFYbdsLeja0O2Iat2HnWuYTxlmQYW2F2OVbUhLDVNP8q0eptLdjuWuAurOAZTzREsZPpmxOt3pRiLcYZ41LgsyY0lMs8+wtz/Wm7pjFcOyzGmfiCYkIRDOI37ttMRXexk/lopmHTy78HfKtzzoYzVklN3hWPYkuhvxYr1qqxn9lHsndggI9hbw7GK5UOQDbnOj3Jupr+ZE11z3Btc8jNNgvI44eu6/nR069s33VieYfBGWTiqqDFUlgM7qK5zpSC3PStr1JxUd6ouEDFhTJpXKybKYadvLOMuF8OYcvIb8NaPA5MtkR4vCV5B/B6RlqSx4GvJVq9rxVsMxtb3jsF4/r/wfbB+JdEq3fvZMZwhvHNw/bcAegxkpXs1d9anJv7h3mkqpLih8c24/uhKGJyftPujXj9Z1s2PYQVGQPAl4AHOudsOGNNiuRd8RuxVW9D2M8tBnwj96f82MR5L7a3zwkCN4lvRHqHa6t6huvrOocapw+mK2sFY4wRcRw/50ou4zpZary+qCu+HOqe2/vDrTcf2LD3+Z05/7TGbA6nCtZC0WoYERH5x3yJ8BTlVQCP7PKfvDTznM+OlRbc3zlnQ915H5BSclRcoOJCKRkOdrKqwE4cWewk1o7tjrqJkVbrY2Z1xFuSzwP+LyNNt5qxAb/vTLR6mWCbGDaGaCY2EHg8pgfn/LtEq1eSySnekpwWnLuCgsZmBp/ssgdn5Vb9aAWZSFaysVMnej8cxcll/OZdG4kMlbKpW4wRi8NngN8HDcfGJXlXfCY2jmll8BrqgQPG4aO5d7Askwu9ty9ZXXm4Nx7tHa5rNjhiQFzJZV0nN0EPEENVdCAScTLhnmRd7hfPvLjrt/ue23uga8GQwck3NDuO7XeSd7l1Y101+WUAG/OTKdVnpigXgstaXIzXAGd0Y7FR+9zJ6QGWp2WgXAhUXFy0eNgaKhFGGqIdwPat2QLs8hKJjsAi8FXsBDOMnTgrsS6NwwDxlqRg2zy/CNu4bDzyDc3elGj12kvxIuItyVpsDNJ0rGA6jdzMp+oy1/77FThZR1LVNkjSD3u4maTfvOtJwslz1eG3Buvq2IntTLllIpGRvCsewjYYfDuQSZpouN9UNd2XeXnXjypf4b3tpi/G43VtFf3J6n4fd9xJ3hhxsn4obIw4IphAhGTqYt1DDRVdvhdKpnzjHBjOxH7QVNXxYHP1nrNrBKcolwiXtbgoN1RcXDIIVjRUE5jDMxLquXv5LXMfmXl9bnvjyrZEdTxtxJkNtCRavV/ld4y3JF8LvIuJAzgF60r5YKLV+00pBhxYSz4JLOMMcQl+9REvc8PnrzQVHZUMNSGhdL/fvGsTofT5KKXdiBVzW7AdKreOJzLiLcnGPwnd/8rXR/7rvfV0z+w1NZla6XUyhJPfyb1h18xrDlf80fIHF2T9kN+XrEmB4BvHzfqhSP4YruQy1dH+7tpYb3dlZGCwOjowGA0l06NKf1UHC1iXy0PYIPNtVV6iH0UpQ1RclBEqLi5NfJBtjauu8sVtjuaSGQE6vCan26v/7cv2/+STwFYvkeiJtySvxzbRO87pnVoLmQU8CPxzYYvyqRIEmH4UuJ6JrSUnMeFBN3PNN56Vm/1khOpjj+LmzneNlUKR8VUCS0a8JelhX8ergbUAEVJDt0W+XveK8L0LfYSkiWWrpD9y0J/Xe1/t/zr64ut/tnBu/cHK3uHarAiDtbGe9lqvt6c21ttfER5KTqKGKFhrVC0jMTpt2AyzbVg3SRvQUeUl1CWiXNKouCgjVFxcehhgZ8PyJccqZsyL5lJDABkn5NWm+4bWtm856NiPU7qi9e1fuPIdyzc3X3liW9OqE2k3Ot4PtwHrx7890eqddWxDvCXpYlM1X8JIgGkxzDaS25j889dtJDr4Fmw8Qd+ZdjoHNGGIMlx/LPzkm467z/zRcjFuBOt26qHg97LU2VVxR/Tzyxc5e5t7/RoTkbR4kjJtJr7JuSHz2LPX/eH6aCjtYMVdKSZ/YcT1lY/RyWeH9GHjQbqwcTXnyp10QfjQ/R9tveepW8bqXtafaPU0oLMMUHFRRqi4uPQ4WD131r7ahSujudQwYHKOGwLk6uNPPlKRHU4BDLledEfDihu8XDLiGD+Tc0Lm6cZV7b+NP/f4YzOu6+6KNebTHqPY4MS3JVq9PWc7tiC+493Aq7AWi2IvFrOxtSg+kGj1ko1t66/EWj5i2In5/JALuTLYPJ3+5vm42WrclCOZigFnzwv3hPbddFyyscJqn7VAheDzJ6H7B/82ete0Zqfdj5FsE6EecE0tv8q9migVPAdrOWrn3NSsEE6txRKmvFJR5fFD17zgjd++e8xU1ESrp6moZYCKizJCxcWlxYlYc/32xpVXhf1MSozxjYhknLC3qnPbxubhjm6AjBNyN0676upkyKvKNyRz/axUZQYirvEFjLRVz+19KP7cYw/Fb4ocro5/rBRpp4GweAfwZ1hhUeyd+mxsyfwPJlq9kxkxjW3rm4E7gTXYbIlz11s8VVkhA9PjMtQwG8RBchnElkU3oWSIcCpMLpxzD9zQ7u5bP+T0z0xhK/n+BHgi0eq1J++KV2Bf+xuwv58OoAkwfpw/+C+mgQpWYQtjTZSxo4zB44euuUXFRXmj4qKMUHFx6dAXqa7Y3HzldYLx8+3RU260Ym7/od2LevcdBNtC/anmK9b0Rmub863WRyPGpyI7FHZNrqIqPdA7r//Qb8RWdv0DcGgqlUQDYfHmYJmMsIgDjwAfSrR6p5nxG9vWh4G3ArdgXTcT1eeYHAYYrq93+mYuIFNZDwacbBJGXeCM42JCEeNkhIqurIn2dRJKP0xk6JvAE51zNpxS/Cp5V3watmLvy7GCqAsrMhx/Lrv99VRTxUyE4eA5vaAWgYqL8kfFRRmh4uLSYDjkRTdOu+qanLjhkJ9NA6TdSKw21dt+ZfvmLYL9EHc0rFh6vGL63HwsxnhknVDYNbncNUcffyRqMjFGMhOOAPcCv/USiaLjJeItyT8D/g8jtTaK2g0raD48lrAopLFt/bOAD2MDLs/OTeKLyGBzs/TPXEg2Uon4Pk4uderPQAQ/FAUEyaVNZWebqWw/RmQ4iXU3NGBdSn3Y9+uXwIHCLJPkXfE5wG3YFOAc1lpRbyBi5tHjPxtDPY04J90l584yUwaouCh/VFyUESouLn5STiS0afq6a1JutCLv5si4YS+aTQ1efeLJJ8J+Ngewu27xgkRVfFE+FmO84xkRJ+OEo2s7tjzekOweHTBZha3/ALZE+b3AQ14iMW7di3hL8tXAe7Cui2JLWM8GNgLvL3SFTERj2/ombL2Oqzhz9svp+K4j/dNnSv/0hZhQBMllkdypxwisFGCM8fqOm8oTh4n19jJ+S3gPKzTydUj+B3i4c86Gk26P5F3xRVh3yQuDVZ0EQZmmgYh/FX1mPg1EGEbooZTWmTJCxUX5o+KijFBxcXGTcULupuZ1Vw2FK2rybo6sEwo7xvevOrHxsXwA54GaefH9NQuWR/z08Jl+oCk3WrGgb/+O+X0Hz5QiWlhrYQvwI+ARL5E4OfkV1NA4RvGT/SxsufP3TjY7pbFtvQu8DlvIaphiGodZUTFL+mcsxLhhJJu23VjzCPhuFOM4uNmUqTpx0FS2H5tCjY3C92s3cD/wWOecDYfhpLvkT7GFuKLYbJghoMnEiPiLiZkVCDVAmAEcOrHxGQoqLi4HVFyUESouLl5y4jibm6+8oj9S3ZAXFr44bs5xw2vbtzxen+rpBzhcNWv6M3VL10T8dFLMxK22024k1pjsPLq64+ntk0glEKAOW8EzC/wauG/VXzy9PBXy7mBywmIGtnnbewo7tU6Wxrb1K7BuklnB+U93KfiuI/0zZkv/9IX4bgjnNFERuD5EiAx2+VXHDlLR3T2BlaJYhBGhYbDpuD/HWmp2Hf7enjDWVfIabB8Xg/2diYF6Gon5c6k1SwhTySBhkoToQuijzPqFTAYVF+WPiosyQsXFxYmPyNbmNau7og3T8/ETRkTSTiS2vHvnUzMHj7UDHI9Na9jRuGJdyM+mHeNP6LPPuOFoNJsauub4E4+HTG6qk5RroPF4xbRZe+sWT3to9nP3/mz+Hx9uq5lbzB32NGxMxrsSrV7PFM9/ksa29R422DPftdS6eHwRGZg+U/pmLcZ3w7jZNBS+N45jRYUxJtZz1FQfPUh0sJS9S0aTdzX5wbIReCiS83dsuveAW5fxXwS8DOsqMVhrTNYIdTRR70+jklnUmCYMEfoJkcKlD5duHM53obELhoqL8kfFRRmh4uLiw0dke+PK5e2x5tkFgZmScqOxwsyQDq+xblvTqqtcP5d1jD9hrEPOcUMGkauOb3y0Kjs4ZVO7AfbWLZrfVjVncXW6L12dHggjsLtucdePF72i7aH48zozbmSs71MTNjPijkSrV9LvVGPb+nXAhzA0MNiUdXrjS8iFvdMtFY6LH4qAnzOVHYdM9bHDhFPnu9CUi62PEWOku+n2qoz/+D9s7eRPD/XPr0/7zxJbJEsYaUzmmBC1NNPkN+LRQKWppZIKwGEYlxQuWRx8hBSQQsoqQFS2tq++4bX/+T8qLsoYFRdlhIqLiwsfkaebVq/o9BpnFQZmptxoxbThE4mVndt3CtAea6rb3rjyKsf42Xxa6njkAzhXdm7fOG24/cwxCuMdB9hdt2Th4erZCyO5kdgOMT5VmYFI2M+4w6FY5hdzX3TovkUvP3q4Op6fuOuxbcDfkWj1jkz1/BMx63Obrssu/uVn/ek7lpELpyQbLbijD0SF5LKm6sR+U33sMG72Ypl4Xaz7pBLrcnIdYwav6Ui2v/pgf+Y5x4dmNaVyTRHfpCI+RmwMxgC2+qaYEDFqqTcVVBAlaqKEqCSERxinrIposb9z/tyX/O4XKi7KGBUXZYSKi4uHnDjydOPqVV1ew4zCVNKUG61oSHYdW9OxdZuDMe2xpvrtjSvXFSMs8vsXWjymQmGa60RBo5Fcyq3KDERA2Na4sv0HS1/T+fiMa4eNOHckWr29Uz3/eMRbkjOB/w08HxjKzdzsZ9d9Z6XxemMkazKS88JWVBzfZ6qPHcHNXSyiYiLC2PiWSsD3sj7L+tKVy3tTsWefSDrL+tKRulTODRmTDPlkw77xHWPSDmTEkHYwaceQxpRXfMaW7FWveMPg91RclDEqLsoIFRcXB1lxna1Na1b3ROumFQqLtBuJ1aT7Oq9of+op1/hTEhZNyY4jkwzgPIWcOLKtcdVp1pSJEONTnRmoABOeMXj8903Jzs9iU1pLEtsQb0lWAq8H/jxYdTw/LhNKRrMr7luVW/TrZuP1tFHRvQtn4niUSwQHm2USjWX96KyhbGV8KBuZOZQJzRjORRpSuXBtOheuzvrhyowfCpnysVwYgb3Mabxz70/H+hxVXJQJoQs9AEUpJ7LiOlua167ti9Q0jhIWXmVmsHdN+9atUxEWaTfiVWf6u/OulKmObSzRcyZ8x3U6Yk1mWefOx5uSnT7wD8B7kvH4j4D7vUTiwFTGE1QCfR7wt9jYheOM1NZwgWmS9bLhra/5Z3/eH54wVZ13AKuxIvlcBm2eD3xs+u3wcMhhb02EvTWRM+1TNjhHV90SLbntS7mYUHGhKCUi6UbDW5vWXDEYrqwtLNedccOel00Orm3fsjlssrmjFTOadjUsu8I1uUwxwiLrhKKRXDq1pmPrFtf4UzKPp51waEvz2rX94eqGyQgLI+KknYi3qHfv9pnDx/PFpPqx5v7XAq9LxuM7gLuxdTOKCqqMtyTnAn+DLaLVzUgrdwGaseLif4D/tEGjn6exbf0dwHpska/ZnCpGFEW5iFBxoSgloD9cFdvatGZd2o14o4VFJJcevqL9qU1RP53Nd0EN+5nUmdJNwWaGAGZNx9ZN0dykC0EBMBSKRbc0rb0yGfKqJiksJO1EvHn9B3fN7W8bHbyZwVbxBJgPtALDyXj8x8CDwL6x+prEW5IethnYG7EZFoVlyeuwqZ6/A/4t0eq1Fe7bOWeDD/yqsW39Y8Ct2B4lPnAC7emhKBcVKi4U5Szp9BpqtzWuutIgTiSXPpkamnYjnpdNDl7ZvnljNJfK5Et6F1MgC4IiW+KGV3c8/WR1ZmBKboDeSE3l1qY1V+UcNzxe87MxESTtRGLxgcTeBb37286wdXewRLDWjNcD+5Lx+PeBh71Eog8g3pJcB7wfmM6pVocY0Igtuf2PwOZEqzeuWOics2EA+FJj2/oHgDuA67Fukq6iX5+iKOcUFReKchYcrpw1bXf9kjWuyWVDfvakSyDtRmKx7HD/lSc2bwz7mdz2xpXLTsSmzSmmpDeMpJwu7tnzdFOyc0pFqtpjTXU7GlasA0y+j0mRSMqJxmYNHtm/uGfP/knEeKQZsWY0A+8D/rZz/tInPvLsD3mRha9Ylw5F+xhxgTjYKp9DwMeBBxKtXtFujs45Gw42tq3/e2At8E5gKdCLddsoinIB0WyRMkKzRc4fPiK765csPFI5a8FoF0fajcQqMkO9V7Zv3iwY83Tj6lVBEGVR2RmILbI1r+/groVnthqMSaJq9vQ9dYtXFxvXUXj2lBuNTR86fmhF145nziZFwQDHY9OmnaiYtlYwYSOSfHTm9Yd/OfeFxzdOu8r1HTeGbab272db5bOxbb0DPAcrMqaBNg27mHGOrr4l+pNPaCpqGaOWC0WZJEOhWHRb46o1A+GquqifGsaMCIa0G4lVZQZ6rmh/anPKjUaeblp9RdL1KicR62CtBgNH9hfhjjiNQPQsOFI5a2GxcR2nnNuNxpqH2w+frbBIOZHQzobly7q8hpkhk027fm4o5GecGw//bu6zjj66OCdOb9jP/Mfqzu33Ab20Ft0RfkyCeIyHGtvWP4LtWPpWbNCnigxFuQCouFCUSXAi1tywq2HZGl8c9xTEnyGdAAAgAElEQVTBIFYUNKS6jq/q2Lat26uv3dGwYq0RcSYT6xBM7oml3c/snezknnFC7kkrySjRUwQnhcXZpLuC7ZGyu37J6qwTChe+R8PhishwuCI3r+/glrl9BzsdWyxrPdCVjMd/CvwWeMZLJKZcMKpzzoY08NPGtvW/5FSR0YuthqkoynlAxYWiFEFOHNlbt2jB4crZC0Mmmy6MYcina84aPLJ/afczew/UzI8frJm3zDW5TCiXLbrfRcqNVjSkuo6v7Ny+a7KT+0Co0nu6efWVk7SS5MkLi8TKzu27HKbmK804IfeZ+qVLTsSmxUMmmy7s/ppxwtHadG/Hsq5dOyuzQ/n3Li+6YtgCWrcC/cl4/GdYobHNSySmlCEzSmS8AHgzVmQMUUxrd0VRzgoVF4pyBrqjddW7GpatSrpe5eiAzJzjhnLihhf17t0+Y/DY8a1Na1Z2eo2zis0IyZOv3rm64+ltk53cO7zGuh2NK67wxZmUlSRAUm40Nm34RNtURE2eLq++ZkfDijUZJ+wVxpak3YjnGD+3tOeZrbMGjhwf5/jDjAiNKHAz8Gogm4zHfw9sADZ7icSk4zICkfFAY9v6nwPXAX8BrMCm0nZwGbc9V5RziYoLRRmHrLjOnrrFC45VzpjvGN8fPXFnnVAUYGXn9o0hP5t7YsY116ediDdZy0HKjVYUlAUverIzwP7aBXMOVc9d6ppcNpzLTLYrqBUWQyfaVnZNTVj4iOyrXTg3UR1f7Bg/O9pa0ZDqOr6065ldsVwyXeQhU4xknISAG4GbAEnG4zuxQmMTsMdLJIqOJ+mcsyEH/CGIyViBrZHxXGzRrm64fNqdK8r5QMWFooxBe6ypbnf9klVpJ+KF/UxydFpV2o3EornU0MrO7Vs6Yk2NbdVzljjGz03WcpB2I7HadG/H2vYtW0ImV7ylwwmHtjeuXNEdrZ8+WSsJnCyQdVZZIUOhWHR748rV/eHq+sIxBNYKf1n3rqdmDh5tP4v4jSzQHvwtQBzb2MwH0sl4/BEC9wlwbKyiXaPpnLPBANuBDze2rW8C/hh4HTALm0rbhVozFOWsUXGhKAX0Rmoq99UtXNwTqWsOmWxmtFjI35E3DXccntd38OAzDUuX94erG6YywafcaMVUhEVvpKZyW+OqK/ICZzLnhJEYkdmDh/ct6d69byqT/9GKGU2765esMiInA1sLYivaV3Tt2BnLJidrSZlw2EBfsIAtP34jNiDUAL2BC+UxYAdw4kxio3POhg7g241t6/8LuAbrjrkWK2T6C86lKMokUXGhKMBgqMLbV7twQWescZZgzFiTdtYJRYyIs7hnz9M5x3U3TV/3LECmMsFPxWJhgLbqOTP31y5YIcac5qYp6hiBsJjXf3DXgt79bZMVFjlx5Jn6pYuPVcyYF/Yzacf3kwAZNxwFWNS7d9uc/raj56GFZ4YRqwaAh7VC/Enwf28yHn8SeBx4Bjg4nhulc86GLPAI8Ehj2/oGrLvklcACrNDQTBNFmSQqLsqLfqB6jPVJoCJYygkzaoGxTdpOsAjW1J7FTk6ZgVCF21Y9Z8bxyhlzAAnKd59yx2tEJAhUHJrXd3Bvojo+bzBUWTuFOhIQxDnUpXpOrOnY+nSxwiLlREI7Gles6I7WT5/iefHFcbNOKLKod++2uf1tR8+8x6kMhiq8bU2r1gyGKmvzqa5590pldrB3Zef2p6sygxcqdiEZLHmi2I6rL8R+J/xkPL4LeALYCewBOkZbNzrnbOgCftTYtv5eYC5WaLwE65LJWzT60V4mijIhWqHzMiAZj5+HG8kLghssoWAJY/tbRIPFC5a8sKoCGgw0JKpmrzhRMf0KX5yZFdkh1/FzaRAfATG+iDFknLA/FKpw06EIzUPt+404cqxyxjwxxg/7kw6ePBnnMG34RGJF546iUz47vMa6nQ3L12SdUGQq1go4mdUSWta9a+vMwWPtZ97jVI7HpjXsali2xoi4+TTcnOOGsxIKB2XC97nGv5gvJi7286/Eig3BBnHuAp4CdgMHgaOjLRyNbesFG5PxLKxlZAlWXPjYIl2ldP9cFmiFzvJHxYVy2RBvSc7ANrl6HbbmQRrocP0sjcOd4ebh9kjTcEekIdkVaRzurGoabm9e3LM3Ob/3QHo4HItnnLAT8rNp1+TI4Zq0G8ml3Eg254SK6hWSdiJefCCxt9h+HTlxZE/d4oVHK2fOd00u6/q5KdV8yDqhCMCKrh2bm4c7JpXOObq+R76UeNqNeCE/m1nWvWvrZI95ERHGio1KbIdWsKLjEFZ07MB2bT0KHM/X3GhsW18LrAaejS05XsuIVawfzTw5Iyouyh8VF0rZEm9J5jMMrgdeivWhw4hpeyxcbG+KLDbt8Qpgeiwz1DN74LCJDyS8WQNHYvN791fH+xNVM4aOV0ZzqVBOXOOanORwTMqNZpMhL2vEAUbcEQt69++c13/o8DjnPYXC2hpjZasUS8YNe66fy6zp2LqxNt03qTLYA6FKb3vjyjWD4crafH2PvEiqTfd2rOzcvs3LpaYkeC5iHGxRrwqsFSyLFQ4ONsbjALAfaANOpMLS/hefmBn+3dWxOb4rVwFXY7u+5rDWtBS2/LgKjgJUXJQ/Ki6UsiHekqwAFgfL1cAabAxKoa98PAQrKlxgC1CP9blPmDUgxqdxuDO8sHdfxdy+Q5WLe/ZULezdVzdz8GiVGCNZcUOAzBg6trMp2XWIM6Q5ZsV19tUtnH+kctYCx/h+YafVyZJ2IzEvmxxY27Flc0V2uOjjGOBI5axpe+sWrTIi5Otn5Bw3nBM3NKe/bc/C3n0Hy9XXNg7Cqa42l5GW8fm/O4FjbTNC3b+4sTK3eWW0Ysei6PSj09zZQzGnNudIOufi+w4OImlsjEgKG/9zWaW/qrgof1RclBHxlmQPYwd0DgJ/eZ6Hc65xse26ZwWPzVjzdhZ7xziMjfA/U/EmAZqwE8ZhrF++Kth/ymWiXT8rc/sOzVnSs9t/56bPPriia+csYBkjwaU5rHA5mWnSFa2v2dWwbFXKjVacjbWCIGi0Jt3XuaZj69aInym6K2rGCbk7G5Yv6/CaZhUGjmbcsOcYP7uic8eWqbaAL3McRuJ9IsEC9nM2Q544B2aHY8eaQ9HjTW5oz7yIczAeDp9ocMN9VU4oGxIDZH1Hcr4Y33fE+ILxHTG+A0YoKy2X7V+wLPWLr6i4KGNUXJQR8ZbkRC3XN1EwkZUBBnvHl8be/aUZuZMshjBWVMSwd5zV2LvHXs6+i6aDFT1bgA8nWr0ugGQ87mKtIYuw7pZrgRlZceVYxYxZR6pm1qfcaNo1frHVLE8j77ZoHm5PrOjasWsyQZadXkPtroZlq9NOxMtnzeSDUKsz/V2rOrY9PYlKm8r4CCOByK4vuIMxCXfXupHuWjc6WOGEUhFxkhEJJaPipiPi+GUmLvozC5d/PP4DFRdljKaiXj50YCfRyxnBioh6rE89iRUUlVh/eimi/qNY98r/AJ9NtHonJ+MgC2F/sPwi3pKU1e1bX16f6v675V07c9cefax31uCRKoPjOfgyGKrIJF0vixQ3r+T7nMzvO7Bzft+BRLGz0agy5ydLeOfdIPGBxN5FPXsPTLWhmXIahpGUaBwD1UOG6qEsc49ORh9fujw+Pbyc+IUehXIuUXGhlDsC1AGNWBEhWItHb7BMFIcxWRqw4uJfgB8nWr1xJ+N4S3Ih8DdPN69ZC3Q8HH/eoa+sfRu1qZ7QFe1P1Vx5YnP9uhObmpuH2isB4yMMhivTGTcypm8+6HNiVnZu3zhtuL1od05PtLZqR8OK1Sk3Whnx08l8m/a0G4mF/UxqZef2zY3Jrt5JvAeKoigqLpSyw8VaJhqwfu8arKDoKVj6KG0RJAeYiU1bbEm0envG2zDekmzCduZ8OVbkJAqf743WZR+K39T1UPymLmBv01B7+OrjT9Zdd+yxprXtTzVXJwciYowMh7zsUKgig0i+z8nw6o6nN1dnBopyfeXEcfbVLpx3uGr2wsKmbIUNx5Z37twR9dOXx620cskgIrcBXytYtcAYc2CC7e8EWvL/G2POm4tJRNYDvy5Y9XxjzIbzdf4LicZclBFniLl4ivIqYewwEr2fL6KV/z+FtUqksGKig8nFY0yGCqxV5EfA5xOt3pgph0Emy2uANwZjPc4kMwTE+Czr2lV57bHHG248/NsZ8YHDtWk3HKnIDHXP7Tu0KWKyyTMf5bTA0VS+J0rGDXuAWdC7f+d5KuGtXKY8Pv2aW/7sZXefVcyFiHwdK9QnFBcF228Abjqf4qLg3HdiBc5lIy7UcnH50IS9oy8nCgM6e7CBmF3B+nNNPnU1A3wg0eo9PNZG8ZZkFHgxtptnNXBiquMz4rCzccXgzsYVg99a9abe+uGuult3fvtX79r4GRzMDdjP12ec9yAjIXdP/eIFxyumzyvs4JoPAq3KDPSs6Nqx7QKW8FYUpUxQcXH5sB0N6CwVVdg4joeBTydavROjNwhExR8Bt2Mn/W5sqmspmAYMdcca7viHe9/3FLyPZDweBdYCzwdegLXiGKDLQPpEbFrDnvrFKzNOOFoYW5FxwlEjIvP6D+6a33sgoUGbiqKUAudCD0BRLiHyKaYA7wc+OFpYxFuSXrwl+afAPcB7g9WHKU0acAhbcXQn8JeJVu+p/BNeIpHyEonHvUTi48DLgPcA9yXdaP2Bmnk3HKuc/iwxfiiSS+cbjjkpN1rh5ZJD605senRh7/42FRbKJUpERD4iIgdEJCUiu0XkvSIy4fwmIvNFxBQs6wue+1zB+g3j7P9sEblPRLpEJCki20TkAyISnfi08h4R2RXsc0hEPiYi3jgbv0lEHhGRQRHpF5HficjrR21zy6jXsUREWkVkv4hkg3V3isgDha9JRBaJyA+D8efXHxh1rAMF57lz1HO3TfT+qrhQlOJowhbr+hHwhkSr97vCbJB4S7Ip3pL8C+C/gb/BuidKJSrA9q+YBnwVeHei1esYb0Mvkcguvn3PtsW37zm87o2b+OBz/m/7U81XHqxJ90tDsitWkR2szoobmdt/6Jlrjj/x2GTLgivKRca/YeOq1mLF933YjK0vTLSTMeZAEH/ROsZzfzVRbIaI3IK1XDrAVVjr5EeBDwI/nkDYfAhb8O9G7O/5c9gblR+KnJpzLiKfA74B/Cp4XfOxwaF3i8gHC8Z6dzDWbwSrPoMNWr8O2wPnRLDdSwpeUyPwTeBT2No77wzWrwf+v+DvO4wx8wvOcyewHOt+rjPGfH289wfULaIoZ6IO6wZ5ChuwubPwyXhLcgnwWmxcBdh4h1JWsBSsqOkE/i7R6m2baOOgn8pVWIETz7iRjkdnXn/80ZnX42WHD1x39LH5Nz/z/dwL2n6ViuVSWWw2jaaaKpcyh40xny74/z0ici3wNhH5tjHmoVKeTERmYEX+EPAGY0z+9/5dEVmBFRC3A18ZY3fXGPOBgv8/LiJrgVuxwd7fDM7xcuAO4OFR239QRJ4H3Cki3zfGnHI9CkgYY+4K/m4XkX9iVFYaVnQ8xxjzu+B8X8E24RsMXtsHgbdjhVshbwe+Z4w54zVDxYWijE0l9m7kIPbO5rG8pSLekqzC3nm8Ftt+O4u9O8iNfagpk89EeRD4VKLVmzDbJ96SnIu9ID0bmxmUj/EQYHoyFMs+NOemDz4056b79/z74hrgBuBmbMVQsAJG24crlxr/Nc66G4E3ASUVF8ExK4GvFQiLPHdjxcVtjC0uxhvrrcFxvxmse0fw+NUxtr8beC5WjPzjGM/fU/iPMeZTY2xzNC8sgm1SwC35/0XkAeClInK9MeaRYF00GOPLxjjeaai4UJRTqcVeOLqxZs5fJlq9XLwl6cZbkquA/wW8EPvbGaR0QZqF5K0VSWz62q/PUJCrBvhzrNjJBWPKb1+LzVL5NfC5RKvXDkBroge4PxmP/xRrbv1j4BXY+iBprAVGYzCUS4FDY6zbFTxeeQ7Od13wuHmM59qCx6tExDFBmncBxY61mHNcM8742sZZP5ltvoztJP124JFg3c3AkbzYOBMqLhRlpHlZBNgHfB34PTZuYmW8JXkTNvMj33+kg9JbKfLkrRW/Af410eqNm+ETb0l62GJct2PrexwvGFcY69M9hu1v8uRYx/ASCYMtR/7FZDz+H9h+JzdjXSsGKzLUmqFczIxl0cvHEdWeg/Plj/lpEfn0ONt4WJfjaMtGsWPN//2UjF/+f/o464tJJT/TNvcBR4DXici7AzfI27CioyhUXCiXM5WM/IgfA74N7AVWAf8HG0dRGTzfBRw9h2PJWyuGsKbOh8ezVsRbkiHgRdjaGfVYsdNVcJzpWGHwFeCeRKtXlDjwEok08Dvgd8l4fDbwEuDVWLFzVl1iFeUcUjXGuvzvtph4ojF/ZyJSMc72ecHwVmPMWG6LiSh2rD3YG54lxphxK/6eK4wxORH5D2zsxRtF5OfYG49XFnsMFRfK5YaHnZAFe1f/PaypcjbWz7mckcqZ3dio63NNHdYq8nNss7MxJ/F4S9LF+pH/DzYltotT3TIN2C6vvwK+lGj1jk11QF4icRj492Q8/i3geqxPeBn2vWnn3FluFGWyzAWeHrVuefC4qYj983fxlaPWzx5n+0ex1Xbnj/WkiCwFZo1TiXPuGOvGGuujWBfsfOA0cSEi1wNDxpgt44yxFHwV+ADWNbIAuGeMGJNxUXGhlDshrHUin3s+DGzEioY5wFuwdy4O1mR5lPMXaxDBpqUdBv4x0eqNeSEMRMVzsWbJ2dhma4XR3/ng02ewgZ+jL7RTJrBmPJSMxx8GFmMtGX+M7eHSTelSbRVlqtwC3D9q3euCx68Xsf/u4HEZ8JOC9a8aZ/tvYmOhbhWRO40xJ1sLiIiLvWHZCGwYZ6yjMzDydSsKx/pvWHFxG/CLwo1FZHZw7LcB50xcGGMOisjPsBbMxdhYs6JRcaGUC4KdrKuwvk6XkZ4jPdhy2B72jnsdVkz0Ya0X5ztwMe+68LEXkR8WtmbPE7g/noe9iMzEiopCS4WHtVb0YDNafp1o9SbVr6RYgtiM3cD/S8bjX8a6jF6PtaBksJkm5+TcinIG1onIu7CTcwR7t30j8IXCjIgJ+BnWGvfXIvJbYAf2+33tWBsbY06IyJuB7wL3isj7sb+N+cBHsEK/Zax9gSYR+RhwF/Z383bgDVhx9J2Cc9wvIp8KxnQY+BL2WnUt8FlsTNZ3i3htZ8uXseJirzHm95PZUcXF5cMKzk/PjfOFYAVCXkA4WJGQwk7CQ9hsi0ywbgibLnqhMyCasFaUXwFfTLR6x0dvEDQ5ezE27asJK4IKRUUYa/EYxhbhuS/R6hXVtKwUeIlEN/C9ZDz+A2yE+6uxF3OwQketGco5Y4yuqLdiBfgO7O/iEPA+4JPB9ndSMNmLiAF+Y4xZD2CMGRSRl2ILSj2EvX7cg7UavAa4KdjnfcaYTwT7fF9EDmLjo36FDcROAD8F3mWMORycaz2ndkV9N9YK+TjWCnkC+BjwETOqi6gx5j0i8hg2vfwOrHjfj7WcfN4YkxnnHPuDINBTmqQVNHqj4DUdLCyUNQY/xlooiw7kPHk+7YpaPpyhK+o2yu+in29algwes1y8sQD5lNAt2JTQ04rfxFuSDdjsj1uwF6t8M7Y8IezFM4e9y7kn0er1n+NxF0UyHm/GBpm+BmtNOddZNcolTCm6oirnHhFZgI1niRtjJhXQfUbLxRgqccL2tqNV4vlsbzuGgrts2tsWwRG0cdmFoAorLA5jTaaPjiobLlhf7yux6a4O9nMq/CGHsGmlOaw/956Jyn9fCLxEoh34bjIe/y9gDbbQzguw7qkhbCS83skoykWMiFQCy40x+dT1twDfn6ywgCLERVA//OujTCoTbX8ntjTpBuCmyQ7obAiEhIwWOIpyAajGxn4cx9b6/02i1TvplgpqVNyINekuwgqH0VkYefdHFluV756J6l5cDHiJhI8tlf5UMh7/DLZa6KuwbjmwIkN7mSjKxckC4EERWYe9KXoHU5zHNeZCUUpLDVZYHAX+FXgo0epl4aSVYhE2QOpl2IDMsap8xrCuhRS29sYPEq1eF5cYXiLRjw2W+1kyHp+JvUi9ChsEarBun2IK/iiKcn7ox/4u92LjQf7OGLN1KgdScaEoZ0++wmcYG0z2CWwRrBxAvCVZh836uBkbUe5jXR+jBUNemPRgI8IfOFM/kUsFL5E4CtwduE0WYbsvvhSbBQPWDXTeglIVRTkdY8xBbNrpWTOVlusREflI0Pc9JSK7ReS9E7SYBUBE5o/qBb++4LnPFfaZH2f/Z4vIfUHv+aSIbBORDwTNVCY4rbxHRHYF+xwSkY+JiDfOxm8SkUdEZFBE+kXkdyLy+lHb3DLqdSwRkVYR2S8i2WDdnSLyQOFrEpFFIvLDYPz59QdGHetAwXnuHPXcbRO9v8oFIYydHGcCTwB/DfxFotXbAMTiLckXxFuSdwE/xHYpbcBaKY5ig1HB/ganYe/mu7Htjl+baPW+Xy7CohAvkTBeIrHHSyS+ihVb78DGkTjY93EWNphVUZRLmKmIi3/DRoGvxfaYvw/4F+ALE+1kjDkQBHe2jvHcX00U+CkitwAPB+O9CptH/FFsadIfTyBsPoT1Wd+IvYB/Dng/8EMZVbBdRD4HfAObVhTH3mH+GrhbRD5YMNa7g7F+I1j1GWyq4HXYNrYngu1eUvCaGrHpQ5/CVmh7Z7B+PXYyAbijMCUoiF1ZjjWb1wWxL8qFR7AiYRbW0vAD4NZEq/d+bJrYTfGW5MeAe4EPY0uJH8cG1BZmdnjBMaYDvwXeBbwp0er9cqyaF+VIIDR2eonEF7Dukrdjg8eT2PdmFtbve96CwhVFKQ1TcYscNsYUNmt5j4hcC7xNRL5tjClpe1sRmYEtQzoEvKGg/Oh3RWQFVkDcztjtbV1jzAcK/v+4iKzFBtG9kaC9rYi8HJtH/PCo7T8oIs/DBqh+3xhzWvogkDDG3BX83S4i/8Sp1RPBio7n5Au6iMhXgOdghcNXsSLp7Zxeue3twPeCpjHKhSXfh0SwZXr/G1uitwm4Ot6S/ACwMtg2gxWZo1PtHKzQDGMF6Vexro+LKvPjQhAU6XoGeCYZj38TWz31Gmx6az4YNMtIQTRFUS5ipiIuxutHfyO26E9JxUVwzErga2PUNb8bKy5uY2xxMd5Ybw2O+81g3TuCx7Ga0NyNLXryRmzBlNHcU/iPMeZTY2xztLBSnDEmha1lAICIPAC8VESuz7ezDdw9b8IG/ikXhny1T7CujO9hG5w1YyvlvTP4G6z4Ha/aZ01wLIO1UtwLbMoHeiqnEgiNQ8Hy38l4vAZbrOt5wA3YgNd8ufY+NMVVUS46piIuiu1HXyqK6Wt/lYg4xpjRd4rFjrWYc1wzzvjaxlk/mW2+jA1uezvwSLDuZuBIXmwo5wUX20TMw05YCWyFug6siHgh8NbgOYNNqzwyzrEKhcl+rPj9TaLVK7rxj2LxEok+7E3LQ8l43AUWYn+/67HWonxvmH6s4FCxoSgXmKmIi2L70ZeK/DE/LSKfHmcbD3shH33hLnas+b+fGhWKUcj0cdYXk0p3pm3uw05SrxORdwdukLcxhZKryqQIYbMzYlgXhgD7sGKwAhs1/efY2hOCnbwmamyWr21hsIGb3wF+m2j1RrvJlCniJRI5bB+H3cA9yXi8AluE7EqshXEh9rPMWzYG0J4ninLemYq4KLYf/XiMeWEWkfEixPOC4a3GmLHcFhNR7Fh7sL7zJcaY09rbnmuMMTkR+Q9s7MUbReTnWLP7K8/3WMqYCFYwVGC/9xFGqmH2Yr8rIWwRmUXYbI4BTq9BUYiLFab57KO92LoUjwIHCitxKucGL5EYwsbAbAK+lozHq7BiYxW2gNeyYFMXWzdkAE15VZRzzlTExVxsrfFCxupHPx75u/jKUetnj7P9o9h+BfPHelJElgKzxinzPXeMdWON9VFse9v5wGniQkSuB4aMMeesvS023uMDWNfIAuCeMWJMlNNxsAGSYaxgiAVLJHjexX7XDDYg0GC/g4PB/1HsnW0PdvKZCMGKkOpgHwM8iW2JvFEDMy88XiIxgP1MngS+mYzHo1hrxmLgamyW22ysNcpl5Ltwps9eUZRJMBVxcQu2PWwhrwsev17E/ruDx2XATwrWv2qc7b+JLeV9q4jcaYw5GQQnIi42yG4jtr/9WGMdnYGRr1tRONZ/w4qL27ATxUlEZHZw7Ldhm06dE4wxB0XkZ9jqjYux/v1Sci3l5YsWRlIUc8GSZaSZWSpYl8GW1R4O1qUp3kzuYoVEBSNukz3Y79wm4JnLJW30UsVLJFLYbpk7sPEzJOPxeqx1aiFWbKzEpr3mBUcO+30Zwn6nFEWZJFMRF+tE5F3YyTmCvdu+EfhCYUbEBPwMe7H/axH5LfZH/2Ls5HcaxpgTIvJmbO/6e0Xk/ViBMh/bCKqe8fuINInIx4C7sJPM24E3YMXRdwrOcb+IfCoY02HgS9jI/2uxlRJ/E5z/XPNlrLjYa4z5fYmP/RSnNsO61MlbIkrVdTNv4chndRisoNiGtWztAHaXY2Gry42gZfwTwfI9gCAjZS62xs1SrOBYiL3G5bAWMsGKjnwXXo3lUJRxmEpX1Fuxd/E7sBH0h4D3AZ8Mtr+Tgsk+6Bn/G2PMegBjzKCIvBRbUOohbJDcPVirwWsY6TP/PmPMJ4J9vi8iB7GpoL/C3kkmgJ8C7zLGHA7OtZ5Tu6K+Gxvk9TjWFHoC+BjwETOq17wx5j0i8hi23sUd2AvHfqzl5PPGmMw459gfBIGe0oF1VKO3/Gs6WFgoawx+jBUA5yKQM436mgU7WXiMpDPmJ44MVrRuxWYUHQAO5Ut4K+VNkJHydLA8AJCMxwV785KvwjoHKzzmYQO8HUYERij4O12wZFABolymyKg5VrmAiF01wXUAAAOGSURBVMgC7MUtPpUWt/GWZI6xXR8OVpRdcs2vJkCwryu/uIzEX4QYMW/nYyPyQroDK0x3Y8XjEWwGSHui1dOJQCmKQHjUYiv/NmOrts7AWj6mB0sdIwI2/7vMW0Dy6/Pf0cK/899ZM+rvckEen37NzX/2srvH+r1JotVzz/uIlJKjjcsuICJSCSw3xjwZrHoL8P2pCIsiWHcOjnmhyV988xfvfNxFhhGXSa7g/ywjF/6rRx8s3nK5G3aUorn9zEllYnwqMkNObbo3WpPqC9Wk+9zKzKBTkRlyKzMDbk26z61J94Vi2aTjZZOulx12vFzKCfsZJ+RnxTU5cf2cuCZr7Z5lxL66BVrSvcxRcXFhWQA8KCLrsHdB78C2pT4XPHiOjqsoyhgYcRiMVDEYqeJI1XjJcJctt5x5E+VSRsXFhaUfmwK5FxsP8nfGmK0XdkiKoiiKcnaouLiAGGMOYtNOFUVRFKVsmErLdUVRFEVRlHFRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSklRcaEoiqIoSkkJXegBKCWlH6geY30WmHOex6IoijIeWcAdY33/+R6Icm4QY8yFHoOiKIqiKGWEukUURVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkpKi4URVEURSkp/z9zi1/RA3XeZgAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "<Figure size 432x432 with 1 Axes>"
- ]
- },
- "metadata": {
- "needs_background": "light"
- },
- "output_type": "display_data"
- }
- ],
- "source": [
- "from pySankey import sankey\n",
- "import pandas as pd\n",
- "import matplotlib.pyplot as plt\n",
- "\n",
- "df = pd.read_csv('data/fruits.txt',sep = ' ',names=['true','predicted'])\n",
- "\n",
- "#print(df)\n",
- "\n",
- "colorDict = {'apple':'#f71b1b','blueberry':'#1b7ef7','banana':'#f3f71b','lime':'#12e23f','orange':'#f78c1b'}\n",
- "\n",
- "sankey.sankey(df['true'],df['predicted'],colorDict=colorDict,fontsize=20,)\n",
- "\n",
- "plt.gcf().set_size_inches(6,6)\n",
- "plt.show()\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "<H1><center>Thanks for your attention</center></H1>"
- ]
- }
- ],
- "metadata": {
- "celltoolbar": "Slideshow",
- "kernelspec": {
- "display_name": "Python 3",
- "language": "python",
- "name": "python3"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.7.6"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 2
-}
diff --git a/notebooks/6a--CUDA.ipynb b/notebooks/6a--CUDA.ipynb
deleted file mode 100644
index a384fc853bc5c9b924014efadd0e4df924bf0a27..0000000000000000000000000000000000000000
--- a/notebooks/6a--CUDA.ipynb
+++ /dev/null
@@ -1,539 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Python for Scientific Computing\n",
- "## Sebastian Ohlmann, Klaus Reuter\n",
- "## Max Planck Computing and Data Facility, Garching"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Using CUDA with Python\n",
- "\n",
- "* pyCUDA\n",
- "* CUDA kernel, wrap using Cython\n",
- "* Numba"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## pyCUDA\n",
- "* [Documentation](https://sysbio.ioc.ee/projects/f2py2e/usersguide/index.html)\n",
- "* Usage:\n",
- " * Write the CUDA kernel in a python string (might be parametrized)\n",
- " * The code is compiled and loaded to the GPU behind the scenes\n",
- " * Block and grid layout have to be specified\n",
- " * Arrays are copied back and forth\n",
- " * No cleanup needed"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "## pyCUDA example\n",
- "* simple multiplication"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "outputs": [],
- "source": [
- "import pycuda.autoinit\n",
- "import pycuda.driver as drv\n",
- "import numpy\n",
- "\n",
- "from pycuda.compiler import SourceModule\n",
- "# define source module with CUDA code in a string\n",
- "mod = SourceModule(\"\"\"\n",
- "__global__ void multiply_them(float *dest, float *a, float *b)\n",
- "{\n",
- " const int i = threadIdx.x;\n",
- " dest[i] = a[i] * b[i];\n",
- "}\n",
- "\"\"\")\n",
- "# extract function\n",
- "multiply_them = mod.get_function(\"multiply_them\")\n",
- "\n",
- "a = numpy.random.randn(400).astype(numpy.float32)\n",
- "b = numpy.random.randn(400).astype(numpy.float32)\n",
- "\n",
- "dest = numpy.zeros_like(a)\n",
- "# call the function\n",
- "multiply_them(\n",
- " drv.Out(dest), drv.In(a), drv.In(b),\n",
- " block=(400,1,1), grid=(1,1))\n",
- "\n",
- "print(dest-a*b)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## More advanced example: correlation function\n",
- "* Given positions and velocities, compute autocorrelation of velocities depending on distance of particles\n",
- "* Particles at irregular positions $\\to$ quadratic complexity\n",
- "* different versions in `pycuda/correlations`\n",
- " * 2 python versions\n",
- " * cython version\n",
- " * MPI version\n",
- " * pyCUDA version\n",
- "* Parallel versions: need reduce at end"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### python version"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "-"
- }
- },
- "outputs": [],
- "source": [
- "def velcorrelation(pos, vel, real_edges, nbins):\n",
- " # return arrays\n",
- " velcorr = np.zeros((nbins,6), dtype=np.float64)\n",
- " numbin = np.zeros(nbins, dtype=np.int64)\n",
- " # loop over given cell indices\n",
- " for k in range(pos.shape[0]):\n",
- " # loop over particles with index smaller than k\n",
- " for j in range(k):\n",
- " dx = pos[j,0] - pos[k,0]\n",
- " dy = pos[j,1] - pos[k,1]\n",
- " dz = pos[j,2] - pos[k,2]\n",
- "\n",
- " dist = np.sqrt(dx*dx + dy*dy + dz*dz)\n",
- " \n",
- " ind = 0\n",
- " # loop over radial bins\n",
- " for i in range(nbins):\n",
- " if dist < real_edges[i+1]:\n",
- " ind = i\n",
- " break\n",
- " # compute velocity correlation\n",
- " numbin[ind] += 1\n",
- " velcorr[ind,0] += vel[k,0] * vel[j,0]\n",
- " velcorr[ind,1] += vel[k,1] * vel[j,1]\n",
- " velcorr[ind,2] += vel[k,2] * vel[j,2]\n",
- " velcorr[ind,3] += vel[k,0] * vel[j,1]\n",
- " velcorr[ind,4] += vel[k,0] * vel[j,2]\n",
- " velcorr[ind,5] += vel[k,1] * vel[j,2]\n",
- " return velcorr, numbin"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### pyCUDA version\n",
- "* python part:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "def velcorrelation_gpu(pos, vel, real_edges, nbins):\n",
- " npart = pos.shape[0]\n",
- " # generate code\n",
- " codefinal = code.substitute(npart=\"%d\"%npart, nbins=\"%d\"%nbins)\n",
- " mod = SourceModule(codefinal)\n",
- " func = mod.get_function(\"velcorrelation\")\n",
- "\n",
- " # return arrays\n",
- " sumcorr = np.zeros((nbins,6), dtype=np.float64)\n",
- " numbin = np.zeros(nbins, dtype=np.int64)\n",
- "\n",
- " func(cuda.In(pos.astype(np.float64)), cuda.In(vel.astype(np.float64)), \n",
- " cuda.In(real_edges.astype(np.float64)), \n",
- " cuda.InOut(sumcorr), cuda.InOut(numbin),\n",
- " block=(512,1,1), grid=(4096,1))\n",
- "\n",
- " return sumcorr, numbin"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### pyCUDA version\n",
- "* array initialization:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "from string import Template\n",
- "code = Template(\"\"\"\n",
- " #include <stdio.h>\n",
- " #include <math.h>\n",
- "\n",
- " __global__ void velcorrelation(double *pos, double *vel,\n",
- " double* real_edges, double *velcorr, unsigned long long int *numbin) \n",
- " {\n",
- " const int npart = ${npart}; // templated here!\n",
- " const int nbins = ${nbins}; // templated here!\n",
- " double dx, dy, dz, dist;\n",
- " int i, j, k;\n",
- " unsigned long long int numbin_cache[nbins];\n",
- " double velcorr_cache[nbins*6];\n",
- "\n",
- " for (k = 0; k < nbins; k++)\n",
- " {\n",
- " numbin_cache[k] = 0;\n",
- " velcorr_cache[k*6+0] = 0.0;\n",
- " velcorr_cache[k*6+1] = 0.0;\n",
- " velcorr_cache[k*6+2] = 0.0;\n",
- " velcorr_cache[k*6+3] = 0.0;\n",
- " velcorr_cache[k*6+4] = 0.0;\n",
- " velcorr_cache[k*6+5] = 0.0;\n",
- " }"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### pyCUDA version\n",
- "* main loop:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "\"\"\"\"\n",
- " // static distribution of indices to threads -> get from block and grid dimensions\n",
- " for (i = blockIdx.x * blockDim.x + threadIdx.x; \n",
- " i < npart; \n",
- " i += blockDim.x * gridDim.x) \n",
- " {\n",
- " for (j = 0; j < i; j++)\n",
- " {\n",
- " dx = pos[j*3 + 0] - pos[i*3 + 0];\n",
- " dy = pos[j*3 + 1] - pos[i*3 + 1];\n",
- " dz = pos[j*3 + 2] - pos[i*3 + 2];\n",
- "\n",
- " dist = sqrt(dx*dx + dy*dy + dz*dz);\n",
- " // get bin index for dist\n",
- " for (k = 0; k < nbins; k++)\n",
- " {\n",
- " if (dist < real_edges[k+1]) break;\n",
- " }\n",
- "\n",
- " numbin_cache[k] += 1;\n",
- " velcorr_cache[k*6+0] += vel[i*3 + 0] * vel[j*3 + 0];\n",
- " velcorr_cache[k*6+1] += vel[i*3 + 1] * vel[j*3 + 1];\n",
- " velcorr_cache[k*6+2] += vel[i*3 + 2] * vel[j*3 + 2];\n",
- " velcorr_cache[k*6+3] += vel[i*3 + 0] * vel[j*3 + 1];\n",
- " velcorr_cache[k*6+4] += vel[i*3 + 0] * vel[j*3 + 2];\n",
- " velcorr_cache[k*6+5] += vel[i*3 + 1] * vel[j*3 + 2];\n",
- " }\n",
- " }"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### pyCUDA version\n",
- "* reduction over threads:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "\"\"\"\"\n",
- " // Reducing velcorr and numbin\n",
- " for (k = 0; k < nbins; k++)\n",
- " {\n",
- " // reduce in block\n",
- " numbin_cache[k] = blockReduceSum(numbin_cache[k]);\n",
- " velcorr_cache[6*k + 0] = blockReduceSumf(velcorr_cache[6*k + 0]);\n",
- " velcorr_cache[6*k + 1] = blockReduceSumf(velcorr_cache[6*k + 1]);\n",
- " velcorr_cache[6*k + 2] = blockReduceSumf(velcorr_cache[6*k + 2]);\n",
- " velcorr_cache[6*k + 3] = blockReduceSumf(velcorr_cache[6*k + 3]);\n",
- " velcorr_cache[6*k + 4] = blockReduceSumf(velcorr_cache[6*k + 4]);\n",
- " velcorr_cache[6*k + 5] = blockReduceSumf(velcorr_cache[6*k + 5]);\n",
- "\n",
- " // reduce among blocks\n",
- " if (threadIdx.x == 0)\n",
- " {\n",
- " atomicAdd(&numbin[k], numbin_cache[k]);\n",
- " atomicAdd_d(&velcorr[6*k + 0], velcorr_cache[6*k + 0]);\n",
- " atomicAdd_d(&velcorr[6*k + 1], velcorr_cache[6*k + 1]);\n",
- " atomicAdd_d(&velcorr[6*k + 2], velcorr_cache[6*k + 2]);\n",
- " atomicAdd_d(&velcorr[6*k + 3], velcorr_cache[6*k + 3]);\n",
- " atomicAdd_d(&velcorr[6*k + 4], velcorr_cache[6*k + 4]);\n",
- " atomicAdd_d(&velcorr[6*k + 5], velcorr_cache[6*k + 5]);\n",
- " }\n",
- " }\n",
- " }\n",
- " \"\"\")"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### pyCUDA version\n",
- "* reduction in warp (smallest unit on GPU, executes one common instruction at a time):"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": [
- "\"\"\"\"\n",
- " __inline__ __device__\n",
- " double warpReduceSumf(double val) {\n",
- " for (int mask = warpSize/2; mask > 0; mask /= 2) \n",
- " val += __shfl_down(val, mask);\n",
- " return val;\n",
- " }\n",
- "\n",
- " __inline__ __device__\n",
- " double blockReduceSumf(double val) {\n",
- " static __shared__ double shared[32]; // Shared mem for 32 partial sums\n",
- " int lane = threadIdx.x % warpSize;\n",
- " int wid = threadIdx.x / warpSize;\n",
- "\n",
- " val = warpReduceSumf(val); // Each warp performs partial reduction\n",
- "\n",
- " if (lane==0) shared[wid]=val; // Write reduced value to shared memory\n",
- "\n",
- " __syncthreads(); // Wait for all partial reductions\n",
- "\n",
- " // read from shared memory only if that warp existed\n",
- " val = (threadIdx.x < blockDim.x / warpSize) ? shared[lane] : 0;\n",
- "\n",
- " if (wid==0) val = warpReduceSumf(val); // Final reduce within first warp\n",
- "\n",
- " return val;\n",
- " }\n",
- "\n",
- "\"\"\"\""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "## Some timings\n",
- "\n",
- "* Timings on a Tesla K20 (Kepler) for 1000 elements:\n",
- "\n",
- " gpu took 0.24s,\n",
- " cython took 0.030 s,\n",
- " python v1 took 5.94 s,\n",
- " python v2 took 8.28 s\n",
- "\n",
- "* Timings on a Tesla K20 (Kepler), MPI on 10 cores (Ivy bridge) for 20000 elements:\n",
- "\n",
- " gpu took 0.25 s,\n",
- " cython took 23.18 s,\n",
- " mpi took 2.41 s\n",
- "\n",
- "* Timings on a Tesla K20 (Kepler), MPI on 20 cores (1 Ivy bridge node) for 40000 elements:\n",
- "\n",
- " gpu took 0.30 s,\n",
- " mpi took 4.85 s\n",
- " \n",
- "* Timings on a Tesla K20 (Kepler), MPI on 20 cores (1 Ivy bridge node) for 100000 elements:\n",
- "\n",
- " gpu took 0.8 s,\n",
- " mpi took 29.77 s\n",
- " \n",
- " \n",
- " ** $\\to$ for some problems, GPUs are very effective! **\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## CUDA kernel *plus* Cython interface\n",
- "Usage:\n",
- "* create a library (shared object, `.so`) of your CUDA device code (compute kernel) and the host function (memory allocation, transfer, kernel launch, transfer, deallocation), e.g. \n",
- " `nvcc --shared -o libhello.so hello.cu --compiler-options '-fPIC'`\n",
- "* write a Cython interface for the host function\n",
- "* proceed as shown in `cython/c_interface_shared_object` \n",
- "\n",
- "Note for completeness:\n",
- "* it is possible to compile both the CUDA code and the Cython interface into the same shared object (Python module), though not recommended"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "### Application: Cadishi\n",
- "* joint project: MPI for Biophysics and MPCDF\n",
- "* purpose: compute radial distribution functions from MD trajectories\n",
- "* parallelization approach\n",
- " * Python multiprocessing\n",
- " * CPU C++ kernel, GPU CUDA kernel, Cython interface\n",
- " * HDF5 IO\n",
- "* see `setup.py` for an example `nvcc` invocation\n",
- "* https://github.com/bio-phys/cadishi\n",
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "source": [
- "## Numba\n",
- "\n",
- "* Numba supports the implementation of CUDA kernels directly in Python\n",
- "* fully transparent handling of NumPy arrays\n",
- "* advanced features: explicit device and memory management possible, streams, atomics, etc.\n",
- "\n",
- "Example below adapted from\n",
- "https://numba.pydata.org/numba-doc/dev/cuda/kernels.html"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "slideshow": {
- "slide_type": "subslide"
- }
- },
- "outputs": [],
- "source": [
- "import numpy as np\n",
- "from numba import cuda\n",
- "\n",
- "@cuda.jit\n",
- "def increment_by_one(x):\n",
- " i = cuda.grid(1) # position in the 1D CUDA grid\n",
- " if i < x.size: # check array boundaries\n",
- " x[i] += 1\n",
- "\n",
- "x = np.zeros(1024*1024) \n",
- "\n",
- "threadsperblock = 32\n",
- "blockspergrid = (x.size + (threadsperblock - 1)) // threadsperblock\n",
- "increment_by_one[blockspergrid, threadsperblock](x)"
- ]
- }
- ],
- "metadata": {
- "celltoolbar": "Slideshow",
- "kernelspec": {
- "display_name": "Python 3",
- "language": "python",
- "name": "python3"
- },
- "language_info": {
- "codemirror_mode": {
- "name": "ipython",
- "version": 3
- },
- "file_extension": ".py",
- "mimetype": "text/x-python",
- "name": "python",
- "nbconvert_exporter": "python",
- "pygments_lexer": "ipython3",
- "version": "3.7.6"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 2
-}